Logical.

It’s a word used to refer to something or someone intelligent, wise, or a philosopher. 

But being logical is as simple as being able to reason correctly. As humans, providing justifications or reasoning for a particular conclusion is one of our essential attributes. This thing makes us different from any other creatures on the planet.

Although we can all think logically, we still need to develop this ability. Hence, this reviewer introduces you to the basics of logical thinking that will help you pass logic exams and apply them in real-life scenarios.

Note: This review consists of two parts. The first part deals with a logical syllogism, while the second deals with test-taking strategies to answer non-syllogistic questions.

Click below to go to the main reviewers:

Ultimate Civil Service Exam Reviewer

Table of Contents

• What Is Logic?
• The Truthfulness of a Statement
• Deductive and Inductive Reasoning
  • 1. Deductive Reasoning
  • 2. Inductive Reasoning
• Logical Syllogism
  • Syllogism Types
    • 1. Universal Syllogism
    • 2. Particular Syllogism
• Download Article in PDF Format
• Test Yourself!
  • 1. Practice Questions [PDF Download]
  • 2. Answer Key [PDF Download]

What Is Logic?

Logic is the study of proper reasoning. In simple words, we use logic so that we can provide correct justification or reasoning for why certain statements hold.

For example, if someone claims that the Earth is round, we can use logic to justify his/her claim. We can do this by providing evidence or arguments to support the claim.

Have you ever watched a courtroom drama where attorneys defend their clients? These attorneys provide arguments to show that their client is not guilty. This is similar to what we do in logic. We provide arguments, reasons, and justifications to prove or assert a particular idea or statement. 

The Truthfulness of a Statement

We have stated earlier that we use logic to prove or assert something. But what exactly is this that we are proving?

In logic, we aim to evaluate the statement’s truthfulness. In other words, we want to conclude whether a particular statement is true or false.

Suppose that you are given this information:

• Some pianists know how to play the guitar
• Selene knows how to play the guitar

Using the information above, can you tell whether the statement below is true or false?

Selene is a pianist

Using logic, we can determine the truthfulness of the last statement. Remember your guess for this example, as we will reveal the answer as we go along in this review.

Deductive and Inductive Reasoning

There are two approaches to thinking logically – deductive and inductive.

1. Deductive Reasoning

In deductive reasoning, you start with a general idea going down to a specific one. In this form of reasoning, you start with a premise. A premise is a fact or rule that serves as your foundation. Using these premises, you conclude. 

Here’s an example:

Premises: 

All birds are mammals

Ostrich is a bird

Conclusion:

Ostrich is a mammal

The given premises established two facts: First, all birds are mammals, and second, an ostrich is a bird. These facts are considered true since they are the premises.  Using these premises, you can conclude that an ostrich is a mammal.

In this reasoning, you start with premises to arrive at a conclusion. This is deductive reasoning. Note how you start with general information about birds being mammals until you arrive at a specific idea that an ostrich is a mammal.

2. Inductive Reasoning

Opposite to deductive reasoning, inductive reasoning starts with specific ideas going down to general ideas. In this approach, you start with one specific thought, recognize a pattern, and then generalize your initial thought to a broader context.

Here’s an example:

• Specific Idea: Regine’s mother is very caring and understanding
• Pattern observed: The mothers of my friends are also caring and understanding
• General Idea/Conclusion: All mothers are caring and understanding.

In our example, we started with the speaker observing that Regine’s mother is caring and understanding. He observed the same thing in all his friends’ mothers. After recognizing this pattern, he can conclude that all mothers are caring and understanding.

In this review, we will focus more on deductive reasoning and its famous form known as a syllogism, as these are the common logic questions appearing in qualifying and assessment exams.

Logical Syllogism

Syllogism is the most basic logical reasoning you will encounter in logic exams, such as in the Analytical Ability subtest of the civil service exam. 

A syllogism is a form of deductive reasoning with two premises that lead to a conclusion. Usually, your task is to determine whether the conclusion is true or false based on the given premises.

Here’s an example of a syllogism:

All sailors are human

Billy is a sailor

Therefore, Billy is a human

The first two statements are the premises. Meanwhile, the third statement is the conclusion drawn upon these premises. 

Here’s the general structure of a syllogism: 

Note that the first premise All sailors are human states a generalized or broad idea. Hence, the first premise is known as the major premise. The second premise, which is more specific compared to the first one, is the minor premise. 

As long as the major and minor premises are true and properly structured, then the conclusion is also true.

Going back to our previous example:

Major premise: All sailors are human

Minor premise: Billy is a sailor

Conclusion:  Therefore, Billy is a human

Since both the major and minor premise is considered true, then the conclusion is also true. 

Sample Problem: 

All amphibians are vertebrates

Frog is an amphibian

Therefore, frog is a vertebrate

Assuming that the first two statements are true. Is the third statement true as well?

Solution: Since the major and minor premises were assumed as true, then by logical syllogism, the third statement is also true.

Syllogism Types

In this section, we will talk about some types of syllogisms that lead to a true conclusion with the assumption that the given premises are true.

1. Universal Syllogism

This type of syllogism has premises that use the words “all,” “only,” “every,” “none,” and “no” to express a “universal” idea or thought.

Our previous example is an example of a universal syllogism. Here are the first two statements that are assumed to be true.

All amphibians are vertebrates

Frog is an amphibian

Therefore, frog is a vertebrate

Since we assumed that it’s true that all amphibians are vertebrates and a frog is an amphibian, then it makes sense to conclude that a frog is a vertebrate as well.

We can illustrate the syllogism above to show that the third statement (or conclusion) is true.

Let’s start with the major Premise: All amphibians are vertebrates. We illustrate this by drawing a circle named amphibian. Since all amphibians are vertebrates, then the amphibian circle should be inside a larger circle named vertebrates. In this manner, we have shown that the set of all amphibians belongs to the set of vertebrates.

Take a look at the image above. Notice that “frog” is located inside the amphibian circle and in the larger vertebrate circle.

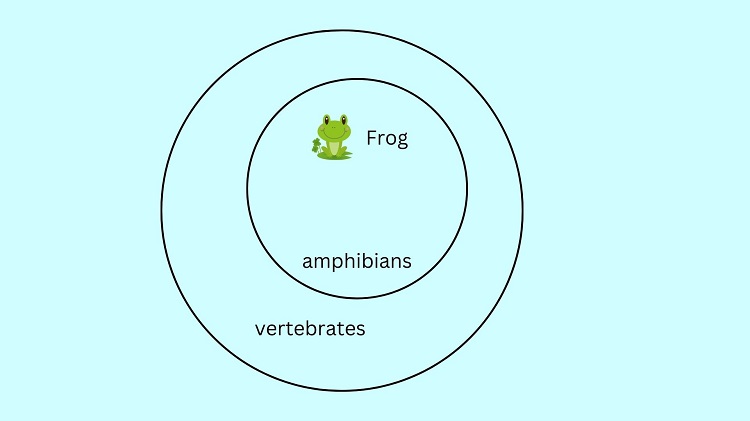
Take a look at the image above. Notice that “frog” is located inside the amphibian circle and in the larger vertebrate circle. This implies that “frog” also belongs to the set of vertebrates. Hence, we can conclude that “Frog is a vertebrate” is true.

Sample Problem 1: If the first two statements are true, determine whether the third statement is true or false.

All plumbers are resourceful

Luke is a plumber

Therefore, Luke is resourceful.

Solution: 

Note that in a syllogism, whether the premises reflect real-world fact is not important. As long as they are used as premises in a syllogism, then the statement is considered true. For instance, the statement All plumbers are resourceful might not be the reality (perhaps you know a plumber who is not that resourceful), but we are assuming it is true since it is used as a premise in the syllogism.

We can illustrate the syllogism above in this way:

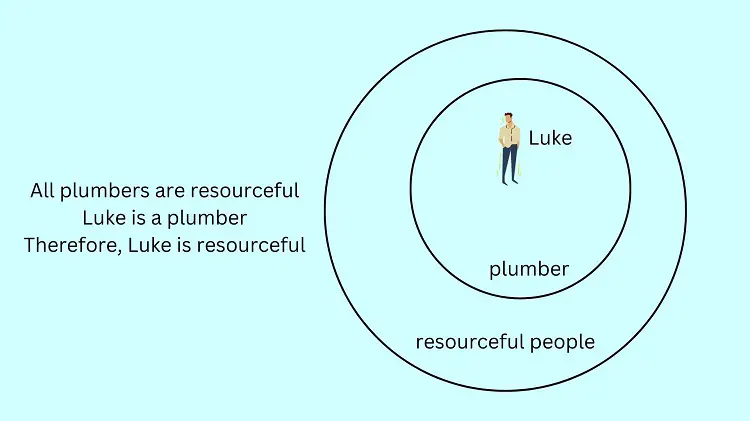
Since “Luke” is located inside the resourceful circle. Then, the conclusion that Luke is resourceful is true.

Sample Problem 2: If the first two statements are true, determine whether the third statement is always true.

All philosophers are intellectual

Friedrich is an intellectual

Therefore, Friedrich is a philosopher

Solution: 

Let us illustrate the syllogism above to answer this example.

All philosophers are intellectual

The major premise is pretty easy to illustrate. However, we have a little problem with the minor premise. It states that Friedrich is an intellectual. This implies that Friedrich belongs to the intellectual circle in the illustration above. However, the minor premise cannot state whether Friedrich is located inside the philosophers’ circle. 

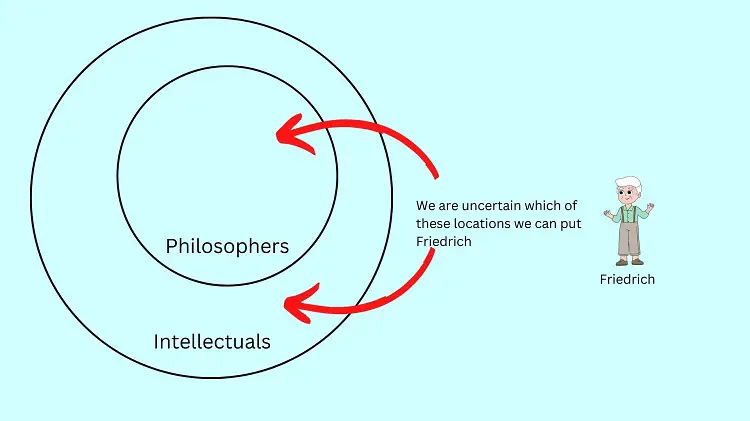
Yes, Friedrich belongs to the set of intellectuals but we are not assured that he also belongs to the set of philosophers. It’s possible that Friedrich is inside the philosophers’ circle or outside it. With this, the conclusion that Friedrich is a philosopher is not always true or uncertain.

Sample Problem 3: Let us look at an example of a universal syllogism that uses the word “No”:

No human being is immortal

All students are human beings

      Thus, no student is immortal

Assuming that the premises are true, how can we show that the conclusion is also true?

Solution: 

Same as with our previous examples, let us illustrate it.

To illustrate No human being is immortal, we create two circles: A human being circle and an Immortal circle. These circles represent this set of all human beings and the set of all immortals respectively. It is mentioned that no humans are immortal. Hence, these two circles must be separated. 

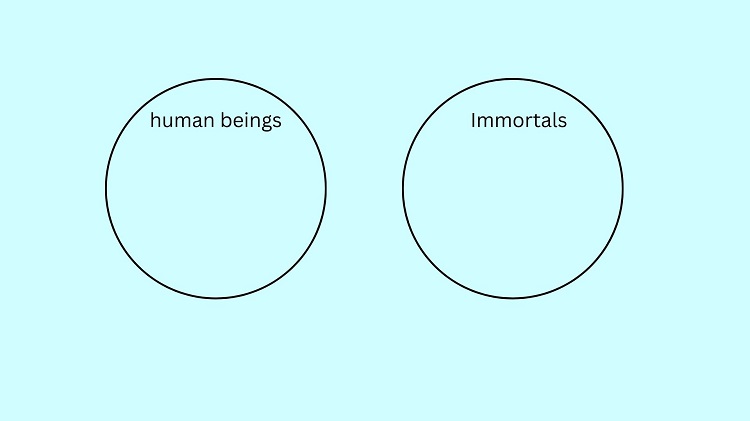
The minor premise states that All students are human beings. Hence, we can put the students inside the human beings’ circle.

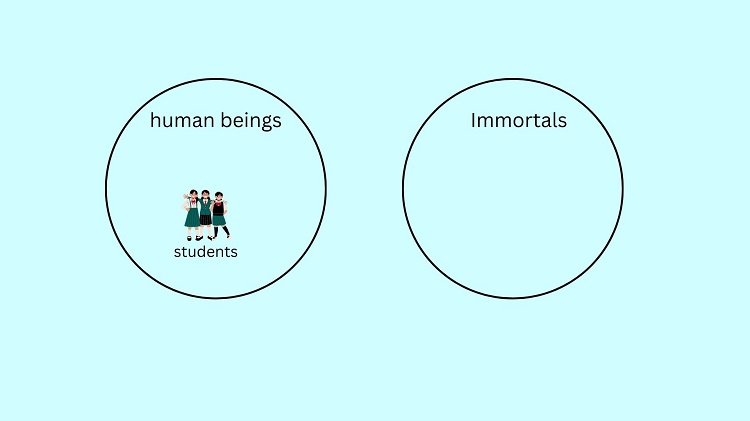
Here, we can see that the set of students which belongs to the set of human beings is not enclosed or included in the set of immortals. This confirms that the conclusion “No student is immortal” is true.

Sample Problem 4: 

No child can drive a car

Sean can drive a car

  Sean is not a child

The first two statements are true. Is the last statement true as well?

Solution:

Here’s the illustration of the syllogism above:

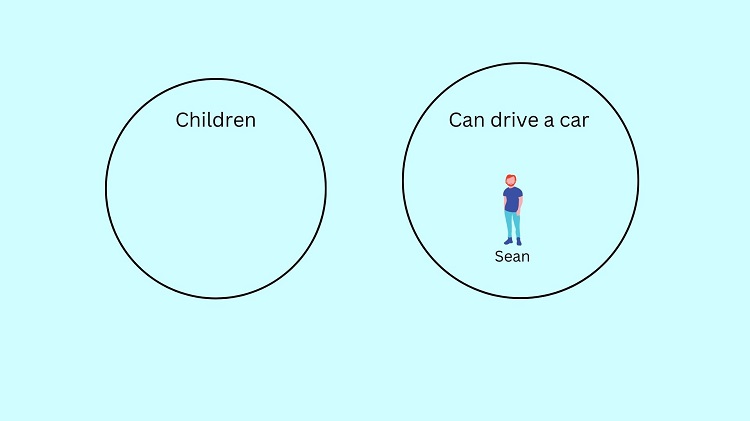
The illustration confirms that the conclusion Sean is not a child is true since it is not included in the child circle.

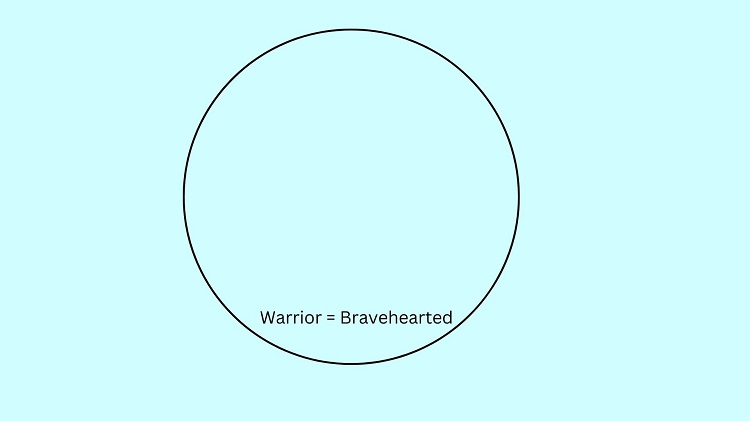
Sample Problem 5: 

Only warriors are brave-hearted

Dustin is brave-hearted

Is Dustin a warrior?

Solution: When the word “only” is used, this means that the set of warriors is identical to the set of brave-hearted ones. If we illustrate it, we just need to label it as “Warrior = Bravehearted” to indicate that this circle pertains to the same set.

If Dustin is included in the set of brave-hearted people, then he should be included as well in the set of warriors since these two sets (i.e., warriors and brave-hearted people) are just the same as mentioned by the major premise.

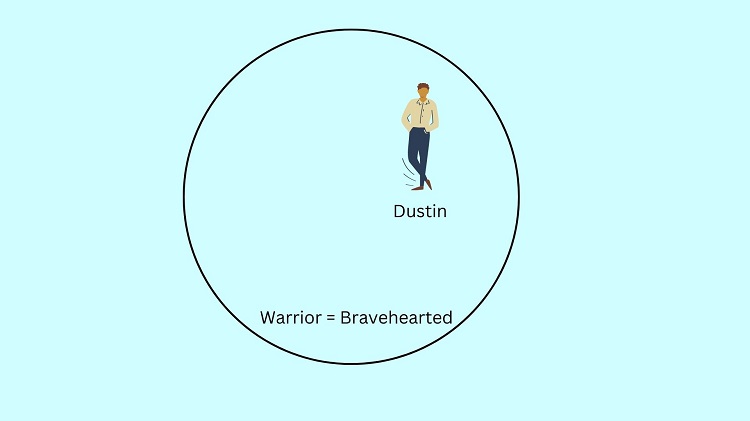
Therefore, we can conclude that Dustin is a warrior.

Sample Problem 6:

All French are Asians

All Asians are Europeans

Are all French also Europeans?

Solution: 

Again, we must accept the premises of the syllogism above as true even if they are far from reality. 

Let us illustrate the given syllogism.

All French are Asians can be illustrated as:

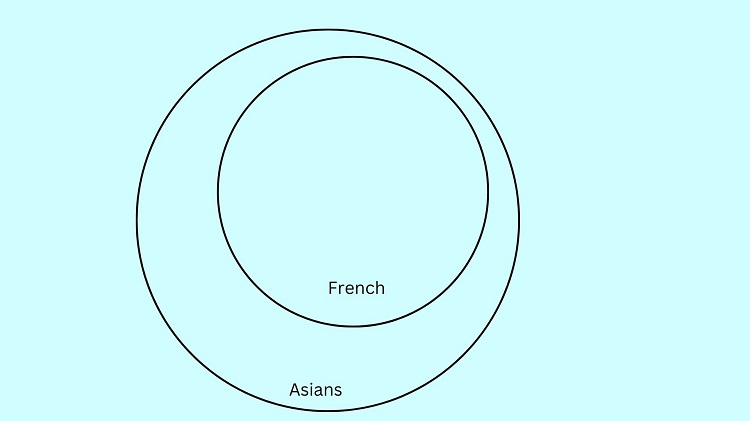
Meanwhile, All Asians are Europeans can be illustrated by putting the “Asians” circle containing the “French” circle inside the “Europeans” circle:

As we can see above, French is located in both Asians and Europeans circles. This implies that all French are also Europeans.

Hence, the conclusion that All French are also Europeans is true.

Sample Problem 7:

Every zoologist is a biologist

All biologists are scientists

Are all scientists also zoologists?

Solution: 

Let us illustrate the premise Every zoologist is a biologist

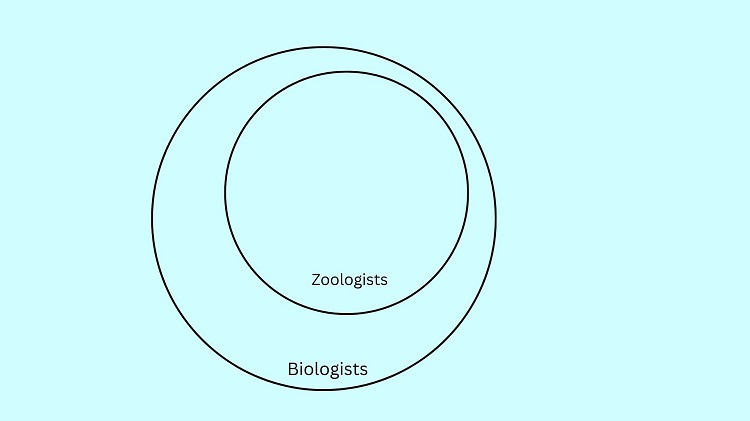
Now, let us illustrate: All biologists are scientists.

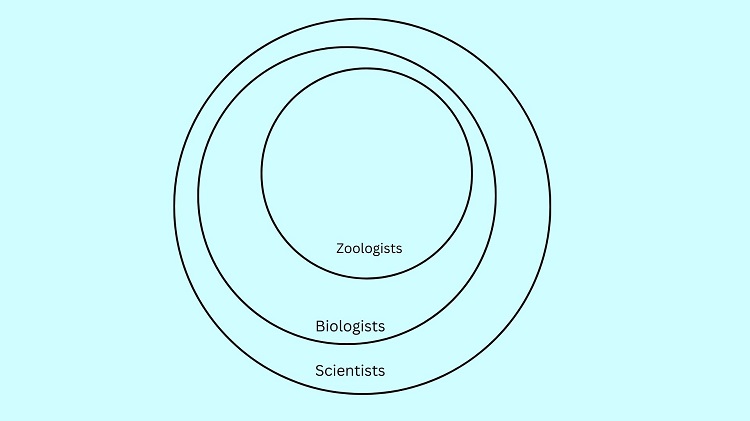
Note that the set of scientists is not contained in the set of all zoologists (i.e., the scientist circle is not contained in the zoologist circle). This suggests that the conclusion that all scientists are also zoologists is not true. 

Sample Problem 8: 

No ring is a necklace

Every piece of jewelry is a necklace

Is a ring also jewelry?

Solution: 

Let us illustrate the premise, No ring is a necklace. Here, we have the ring circle and necklace circle which are separated from each other. 

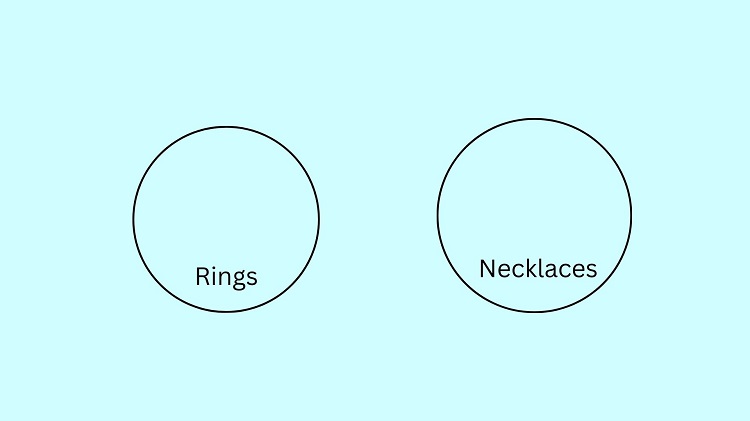
Now, let us illustrate the premise that Every piece of jewelry is a necklace. This means that the set of all jewelry is contained inside the set of all necklaces.

It is clearly seen from the image above that the set of rings is not included in the set of jewelry since the ring circle is separated from the jewelry circle. This implies that a ring is not jewelry.

Again, syllogisms do not have to conform to reality. Although we all know that a ring is jewelry, the premises of the syllogisms allow us to lead to a proper conclusion that departs from this reality.

2. Particular Syllogism

The second form of syllogism involves premises that state particular ideas. Unlike in universal syllogism, the words “some” or “most” are present in the premises.

In a particular syllogism, it’s important to understand that we are not generalizing but we are pertaining only to specific cases.

Here’s an example:

All birds are vertebrates

Some flying animals are birds

Some flying animals are vertebrates

Although the first premise uses the words “All,” the syllogism above is still a particular syllogism since the remaining statements use the words “Some” to imply that the thought does not apply in general.

Take a look again at the previous example. If we assume that the major and minor premises are true, can we also say that the conclusion “Some flying animals are vertebrates” is true? 

If all birds are vertebrates and some flying animals are birds, then it makes sense that some (and not all) flying animals are vertebrates. The reason behind this is that not all flying animals are birds (as mentioned in the second premise).

I know that the explanation above is quite confusing but don’t worry, an easier way to grasp this is through visual illustration.

Let us illustrate the premise All birds are vertebrates. We do this by drawing two circles: a bird’s circle and a vertebrate’s circle. The birds’ circle must be located inside the vertebrates’ circle to indicate that all birds are vertebrates.

To illustrate the second premise, Some flying animals are birds, we need to draw a circle that represents the set of flying animals. Now, should we put this circle inside the birds’ circle in the illustration above?

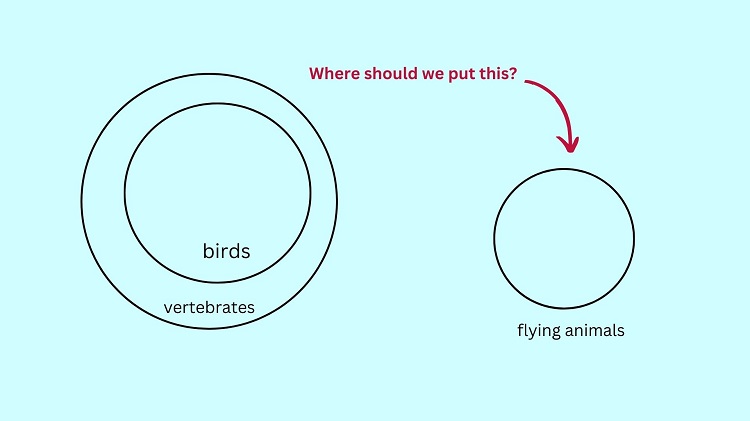
The answer is no. If we put the flying animals’ circle inside the birds’ circle, this means that all flying animals are birds! This contradicts the given premise that some (not all) flying animals are birds.

To illustrate the given premise that Some flying animals are birds, we let the birds’ circle and flying animals’ circle intersect, just like in a standard Venn diagram. This form reflects that some (but not all) flying animals belong to the set of birds.

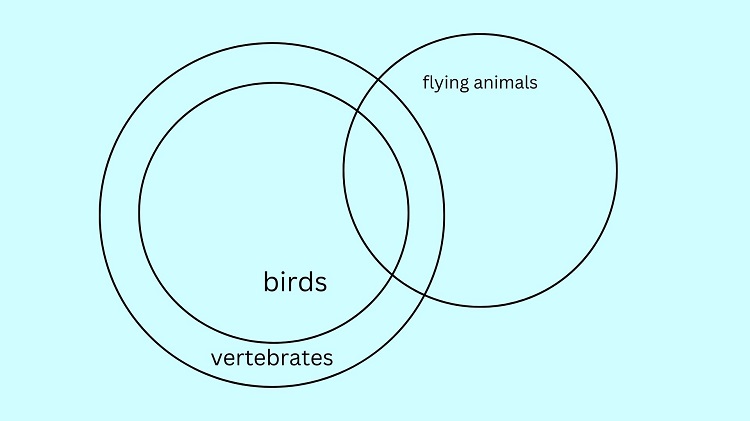
As we can see above, some portion of the flying animals’ circle is located inside the vertebrates’ circle. Notice also that some portion of the flying animals’ circle is located outside the vertebrates’ circle. This confirms that the conclusion Some flying animals are vertebrates is also true.

Sample Problem 1: 

Some kings are rude

Henry is a king

Therefore, Henry is rude

If the first two statements are considered true, are we assured that the third statement is also true?

Solution:

The answer is no. The first premise established that some kings are rude. This means that there are kings that are rude, while there are also those that are not rude. So, if Henry is a king, then we cannot state with 100% certainty that Henry is rude since there are some kings that are not rude. 

Let us illustrate the syllogism above to show our explanation better.

We construct two circles: the king circle and the rude circle (this represents the set of all rude people). To show that some kings are rude, we let the king and rude circle intersect like in a standard Venn diagram. 

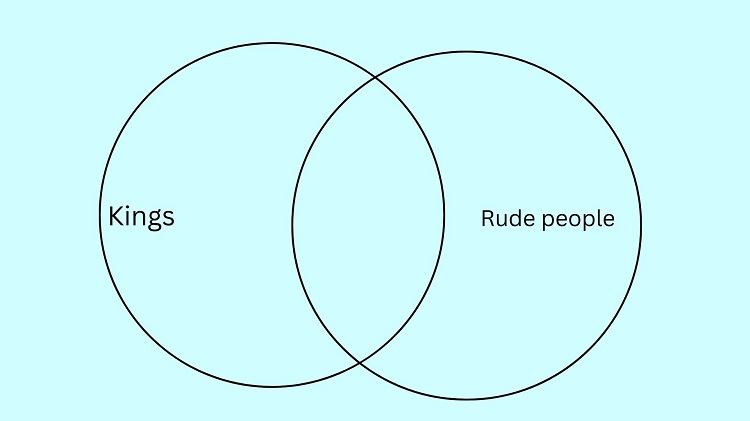
In the illustration above, the intersection of the king and rude circles represents the set of all kings that are also rude. Meanwhile, the portion of the king’s circle that is outside the rude circle represents the set of all kings that are not rude. Here, we’ve shown that some (and not all) kings are rude.

Let us proceed with the second premise: Henry is a king. We do this by simply putting “Henry” inside the king’s circle. 

However, the problem is that we can either put Henry inside the intersection of the king and rude circles or outside of it. Note that whatever we select from the two, it still captures the premise that Henry is a king. 

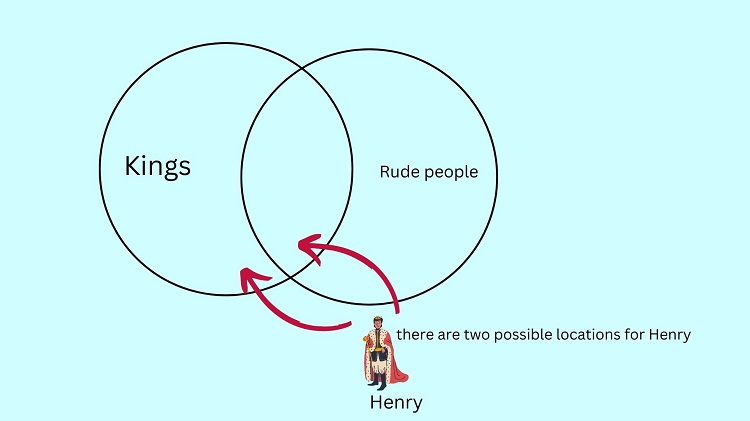
If Henry is located inside the intersection, this means that Henry is also rude. On the other hand, if Henry is located outside the intersection, this means that Henry is not rude. 

As we have mentioned earlier, it’s possible to locate Henry inside or outside the intersection. This implies that we cannot really conclude whether Henry is rude or not. Therefore, we cannot guarantee with certainty that the conclusion Henry is rude is true, given the premises.

Sample Problem 2: 

All philosophers are Greek

Some English are philosophers

Therefore, all English is Greek

Is the third statement true?

Solution:

The first premise states that All philosophers are Greek. Note that this premise is a generalization. The second premise mentioned that some English are philosophers. Note that this premise is not a generalization anymore. There could be English philosophers and there are also those that are not.

Now, can we conclude that all English is Greek? The answer is no. Note that from the second premise, we have mentioned that some English are non-philosophers. Since the first premise states that all philosophers are Greek, then it makes sense that NOT all English are Greek. 

Thus, the conclusion All English is Greek is false.

Now, let us try to answer the same example by illustration.

All philosophers are Greek can be illustrated in this way:

Meanwhile, Some English are philosophers can be illustrated as follows:

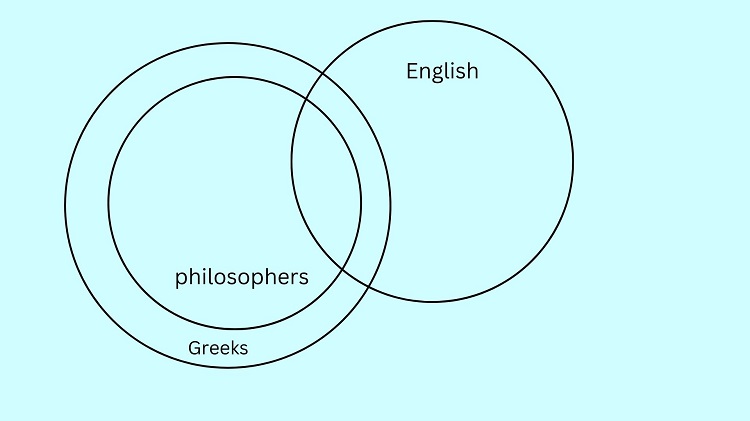
From our illustration above, some portion of the English circle is located inside the Greek circle but there is also a portion located outside it. This implies that it is not true that all English is Greek.

Answering Non-Syllogistic Logic Questions in Civil Service Exam

Logic questions in the Analytical Ability subtest of the CSE do not revolve only around syllogisms. Some are non-syllogistic. 

Like with syllogistic logic questions, we will still use diagrams or visual illustrations to arrive at the best conclusion.

Here are some pointers to remember when creating diagrams to answer logic questions:

• Illustrate one step at a time. Dissect the given question into smaller bits of information to make it easier to create a diagram.
• Label your diagram. Always label every symbol and shape you will use in your diagram.
• Recognize all characters in the given question. If the question involves various names of individuals, make sure that you consider all details about them.

1. Comparing Magnitude Logic Questions

This type of logic question involves a comparison of the magnitudes of the attributes of people or objects (height, weight, price, length, etc.)

Sample Problem 1: Millet is shorter than Iya. Regine is shorter than Millet. Chezka is taller than Iya. Who is the third tallest person among the three?

Solution: 

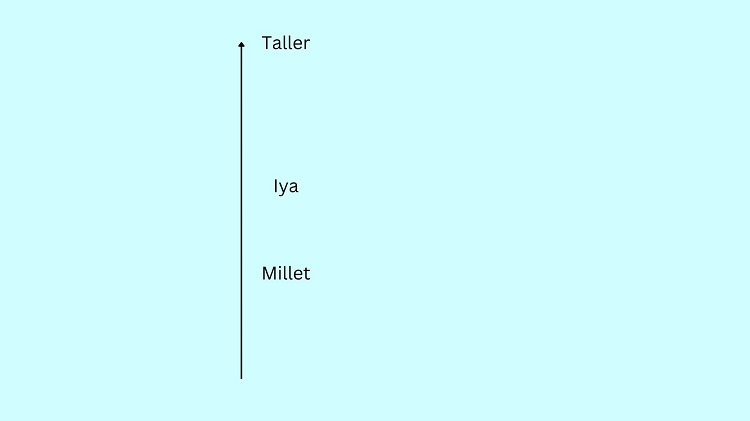
Start by identifying the characters in the given question. Four characters are mentioned, namely Millet, Iya, Regine, and Chezka. 

Let us create the diagram as shown below. In this illustration, as the character goes upward, it means that they are taller. 

“Millet is shorter than Iya.” Hence, we should put Iya above Millet in the diagram. Allot some space between characters since you might insert other characters between them.

Regine is shorter than Millet. This means that we should put Regine below Millet in the diagram.

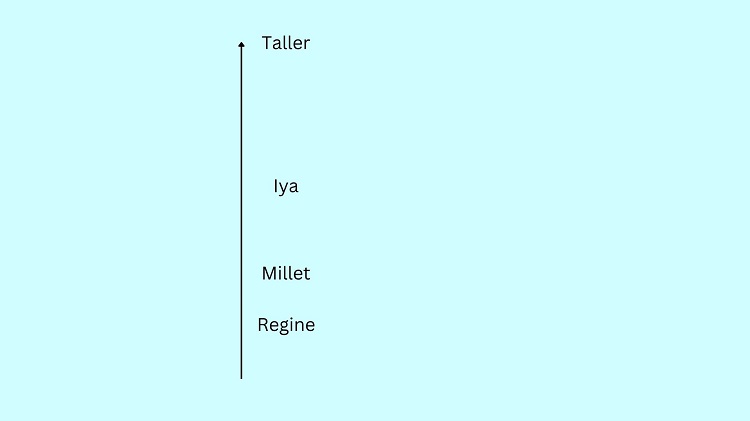
Chezka is taller than Iya. This means that Chezka should be placed above Iya in the diagram.

From the final illustration above, it’s clear that Millet is the third tallest person among the four.

Sample Problem 2: A laptop is more expensive than a notebook. A teapot is cheaper than a laptop. An oven is more costly than a teapot. A plate is more expensive than a notebook but cheaper than a teapot. What is the third cheapest object among the five?

Solution:

Illustrating the problem above, we have:

We can easily see that the teapot is the third cheapest object among the five.

2. Racing Logic Problems

In these logical questions, characters are involved in a race in which some may overtake other players.

Sample Problem 1: Runner A is behind Runner D. Runner C is ahead of Runner A. Runner B is in between Runners A and D. Meanwhile, Runner E is in between Runners D and C. Runner A overtakes Runner E. Afterward, Runner B overtakes Runner D. Lastly, Runner D overtakes Runner A. Which runner is behind Runner A?

Solution: 

Let us start by illustrating the initial positions of the runners:

Runner A is behind Runner D. Runner C is ahead of Runner A. Runner B is in between Runners A and D. Meanwhile, Runner E is in between Runners D and C.

Let us illustrate one-by-one the changes in the position of runners after the overtaking.

Runner A overtakes Runner E.

Runner B overtakes Runner D.

Lastly, Runner D overtakes Runner A.

It can be seen in the last image that Runner E is the one that is behind Runner A.

3. “Either A or B” Logic Questions

In these logical questions, a character faces two possible options such that choosing one option means that he/she discards the other option.

Sample Problem 1: Either Sean will attend the concert, or he will study for his midterm exam. If Sean studied for his midterm exam, then __________________

a) Sean did not attend the concert 

b) Sean attended the concert

c) Sean did not study for his midterm exam

Solution: We can create a flowchart that illustrates the given question. We have Sean doing either of the two: attending a concert or studying for his midterm exam. 

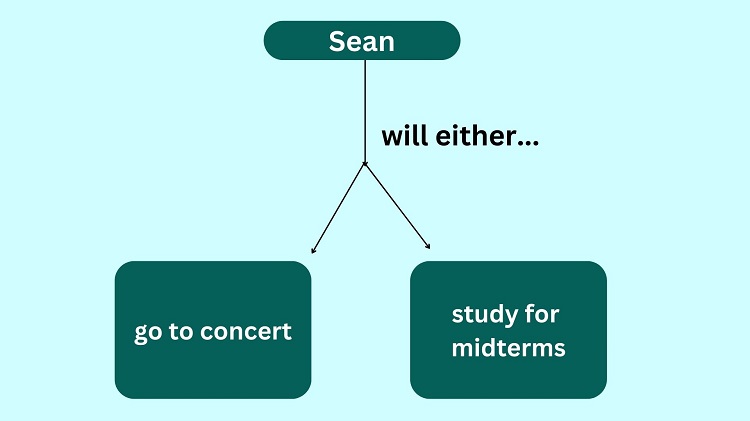
As we can see from the diagram above, if Sean decided to attend the concert, then it already means that he did not study for his midterm exam and vice versa. 

Therefore, if Sean studied for his midterm exam, it follows that he did not attend the concert.

Sample Problem 2: If the inflation rate significantly increases in the next quarter, the Bangko Sentral ng Pilipinas (BSP) will raise the interest rates or sell bonds to the public. Which of the following is necessary for the BSP to raise interest rates?

1. The inflation rate did not increase significantly, and the BSP did not sell bonds to the public
2. The inflation rate significantly increased, and the BSP sold bonds to the public
3. The inflation rate significantly increased, and the BSP did not sell bonds to the public.

Solution: Let us create a flowchart to further understand the given problem.

As shown in the illustration above, if the inflation rate significantly increases, BSP raises the interest rate or sells bonds to the public. Otherwise, nothing will happen.

Looking at the diagram, BSP will raise interest rates if the inflation rate significantly increases and if BSP does not sell bonds to the public. Hence, the answer to this problem is C.

Next topic: Number Sequence

Previous topic: Identifying Assumptions and Conclusions

Return to the main article: Ultimate Logical and Analytical Reasoning Reviewer

Download Article in PDF Format

Test Yourself!

1. Practice Questions [PDF Download]

2. Answer Key [PDF Download]