Number Series Examples and How To Solve
Number series questions require you to crack the pattern among the given numbers to identify the missing one correctly. With ample practice and familiarity with common number patterns, your chances of passing this subtest improve.
This article will provide number series examples and how to solve them. By the end of the discussion, you will be able to answer number series questions commonly appearing in examinations.
Click below to go to the main reviewers:
Ultimate Civil Service Exam Reviewer
Ultimate NAPOLCOM Exam Reviewer
Table of Contents
What Is a Number Series or Sequence?
In plain words, a number series consists of numbers that follow a particular pattern. Each number in a sequence is called a term.
For instance, 2, 4, 6, 8, 10, … is a number series since it consists of numbers that follow a particular pattern.
Can you guess the pattern of the sequence above? Yes, these are the numbers you’ll get if you count by 2’s.
Questions involving number series challenge you to determine the missing term based on the pattern of the given sequence. Here’s an example:
19, 22, 25, 28, _____
What number must be placed in the blank?
To determine the missing term, we must first identify the pattern of the given numerical sequence. By examining the given numbers, we can see that the next term is obtained by adding three to the previous term:
19 + 3 = 22
22 + 3 = 25
25 + 3 = 28
Given this pattern, we can find the missing term by adding three to 28:
28 + 3 = 31
Therefore, the missing term in the given number sequence is 31.
From our example above, we saw how important it is to know the number sequence’s pattern. It will be impossible to guess the missing number if we cannot figure out the pattern. Therefore, learning some commonly used number series patterns in exams is helpful. In our next section, we will discuss these patterns in-depth.
Typical Number Series or Sequence Patterns
| Number Sequence Pattern | Example |
| Arithmetic Sequence | 5, 8, 11, 14, 17, … |
| Geometric Sequence | 5, 10, 20, 40, 80, … |
| Recursive Sequence | 1, 3, 4, 7, 11, 18, 29, … |
| Alternating Sequence | 3, 5, 15, 17, 51, … |
| Perfect Square Number Pattern | 1, 4, 9, 16, 25, 36, … |
| Perfect Cube Number Pattern | 1, 8, 27, 64, … |
| Triangular Number Pattern | 1, 3, 6, 10, 15, … |
| Prime Number Pattern | 17, 19, 23, 29, … |
| Increasing Difference Pattern | 5, 7, 10, 14, 19, … |
| Decreasing Difference Pattern | 72, 70, 67, 63, 58, … |
1. Arithmetic Sequence
Each succeeding term is obtained by adding a number to the previous term. This number that is being added to the terms is called the common difference.
See the example below:
34, 39, 44, 49, 54, …
The sequence above is an arithmetic sequence because a particular number (5) is added to each term to get the succeeding term.
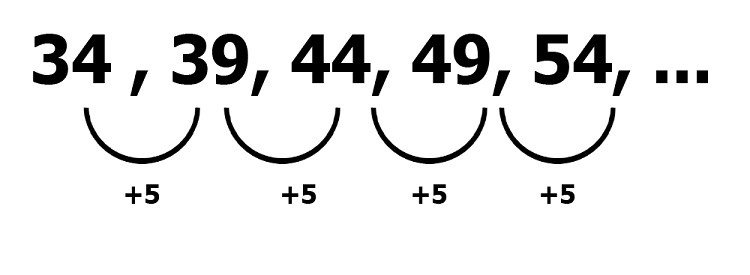
Note that the common difference can be a negative number as well. Here’s an example:
14, 12, 10, 8, 6, …
The common difference in the given sequence above is the negative number 2. A negative common difference also means subtracting a particular number from the previous term to get the next one.
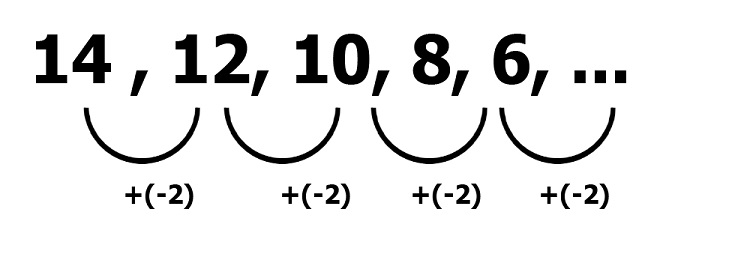
Sample Problem 1: What is the next term in 94, 97, 100, 103, _____?
Solution: The number sequence is an arithmetic sequence with a common difference 3. Hence, the missing number can be found by adding 3 to 103: 103 + 3 = 106. Hence, the missing number is 106.
Sample Problem 2: What are the missing numbers in the sequence 9, 15, ____, 27, ____?
Solution: The number sequence is an arithmetic sequence with a common difference of 6. Thus, to find the missing numbers, we only need to add 6 to 15 and the same with 27.
- First missing number: 15 + 6 = 21
- Second missing number: 27 + 6 = 33
Therefore, the missing numbers are 21 and 33.
2. Geometric Sequence
In a geometric sequence, each succeeding term is obtained by multiplying the previous number by a certain number, called the common ratio.
Like the common difference, the common ratio can be positive or negative.
Below is an example of a geometric sequence:
2, 8, 32, 128, …
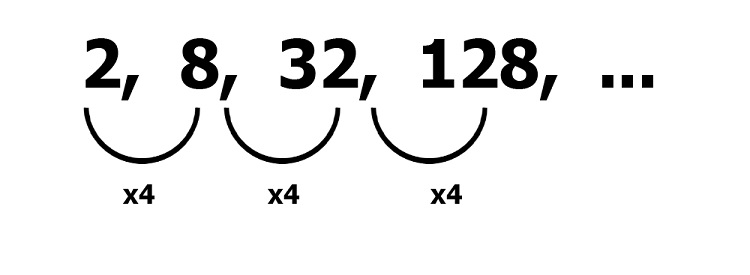
Each sequence term is multiplied by 4 to get the succeeding term. Thus, the common ratio of this geometric sequence is 4.
Sample Problem 1: What number must be placed in the blank to complete the sequence 3, 15, 75, ______?
Solution: This is a geometric sequence with a common ratio of 5. Hence, the missing term can be obtained by multiplying 75 by 5: 75 x 5 = 375. Hence, the missing term is 375.
Sample Problem 2: 72, 36, 18, ______
Solution: In this geometric sequence, the common ratio is a fraction (or decimal) which is ½. This means that to get the next term, we multiply ½ (or divide by 2) the previous term. Note that multiplying a number by a fraction is equivalent to dividing that number by the fraction’s denominator. Thus, a geometric sequence with a common ratio that is a fraction can be interpreted as the division of the terms by a constant number.
72 x ½ = 36
36 x ½ = 18
Therefore, the missing term can be determined by multiplying ½ by 18 (or dividing 18 by 2):
18 x ½ = 9
Thus, the missing term is 9.
3. Recursive Sequence
A recursive sequence is a sequence in which each succeeding term is defined in terms of the previous term.
A common type of recursive sequence is the Fibonacci sequence. We add the two previous terms in a Fibonacci sequence to get the next one.
Here’s an example:
1, 1, 2, 3, 5, 8, …
The succeeding term is obtained by adding two previous terms in this sequence. For example, to get “2,” we need to add “1” and “1” (two terms preceding 2). Similarly, to get 8, we add “3” and “5” (two terms preceding 8).
Sample Problem 1: Find the missing term in 2, 6, 8, 14, 22, ________
Solution: The given sequence is recursive such that the succeeding term is obtained by adding two previous terms. For instance, “14” is obtained by adding two terms preceding it, which are “8” and “6”.
Therefore, to find the missing term. We need to add the numbers preceding the blank, which are “14” and “22”: 14 + 22 = 36.
Thus, the missing number is 36.
Sample Problem 2: Identify the missing number: ____, 6, 10, 16, 26, …
Solution: The given sequence is recursive such that the succeeding term is obtained by adding two previous terms. For example, “26” is obtained by adding two terms preceding it, which are “10” and “16”.
To identify the missing number, we recognize that “10” was obtained by adding “6” and the missing number. Hence, the missing number should be 10 – 6 = 4.
The answer is 4.
4. Alternating Sequence
The mathematical operations are used alternately in an alternating sequence to get the succeeding terms.
Here’s an example:
3, 8, 16, 21, 42, …
In this sequence, “addition” and “multiplication” were used to derive the succeeding terms.
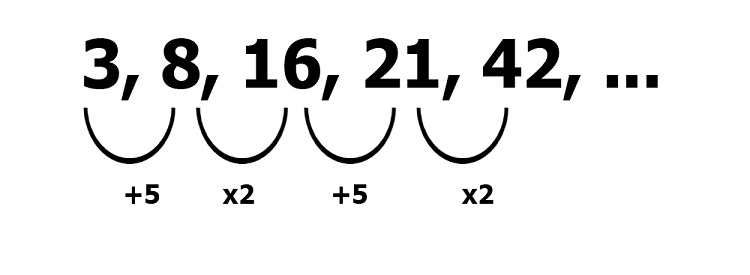
3 + 5 = 8 x 2 = 16 + 5 = 21 x 2 = 42
Sample Problem: Determine the missing term in 6, 7, 21, 22, 66, _____
Solution: The number series alternately adds 1 and multiplies 3 by the terms to get the succeeding terms.
6 + 1 = 7
7 x 3 = 21
21 + 1 = 22
22 x 3 = 66
The sequence ends with multiplication by 3, so the next operation should be the addition of 1:
66 + 1 = 67
Therefore, the missing number is 67.
5. Perfect Square Number Pattern
In this type of sequence, the squares of whole numbers are listed numerically. Recall that the square of a number is the result when you multiply a number by itself.
For instance, the square of 9 is 81 since 9 x 9 = 81.
Here’s an example:
4, 16, 36, 64, 100, …
The sequence above is the squares of the even numbers from 2 to 10:
2 x 2 = 4
4 x 4 = 16
6 x 6 = 36
8 x 8 = 64
10 x 10 = 100
Sample Problem: What is the missing term in 1, 9, 25, 49, _____?
Solution: The sequence above is the squares of the odd numbers.
1 x 1 = 1
3 x 3 = 9
5 x 5 = 25
7 x 7 = 49
The odd number next to 7 is 9. So, to get the next term, we have to square 9:
9 x 9 = 81
Therefore, the missing term is 81.
6. Perfect Cube Number Pattern
In this type of sequence, the cubes of whole numbers are listed numerically. Recall that the cube of a number is the result when you multiply a number by itself thrice.
For instance, the cube of 2 is 8 since 2 x 2 x 2 = 8
Sample Problem: Determine the missing term:
1, 8, 27, 64, 125, ____,
Solution: The sequence above follows the perfect cube number pattern in which the first 5 whole numbers were cubed.
13 = 1 x 1 x 1 = 1
23 = 2 x 2 x 2 = 8
33 = 3 x 3 x 3 = 27
43 = 4 x 4 x 4 = 64
53 = 5 x 5 x 5 = 125
Hence, the missing term should be the cube of 6:
63 = 6 x 6 x 6 = 216
The cube of 6 is 216. Therefore, the missing term is 216.
7. Triangular Numbers Pattern
In this pattern, the numbers form a triangle by visualizing it using dots.
Take a look at the example below:
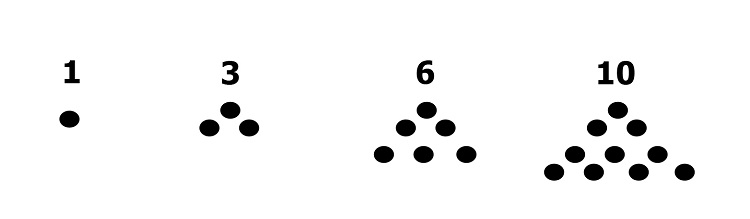
The number sequence 1, 3, 6, 10, …, if visualized using dots, forms a triangle that is increasing in size.
We can determine the succeeding term of this pattern by adding dots to the last triangle. To determine the number of dots for the next triangle, the “side” of each succeeding triangle must be one more than the previous one. In the triangular number 1, the side has 1 dot. In the triangular number 3, each side has 2 dots. In the triangular number 6, each side has 3 dots, and so on.
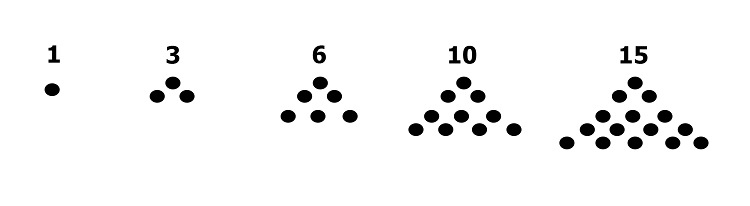
So the succeeding term in 1, 3, 6, 10, … should form a triangle whose “side” has five dots. That triangular number is 15.
8. Prime Number Pattern
In this number pattern, we list the prime numbers in ascending or descending order. Note that a prime number is a whole number whose factors are only one and itself.
Here’s an example of a prime number pattern:
2, 3, 5, 7, 11, …
The numbers above follow the prime number pattern.
Sample Problem: Determine the next term in 17, 19, 23, ________
Solution: 17, 19, and 23 are prime numbers because these numbers have two factors only (1 and themselves). We need to identify the prime number next to 23 to find the missing term.
24, 25, 26, 27, and 28 are not prime numbers (i.e., composite numbers). 29 is the prime number next to 23.
Thus, the missing term is 29.
9. Increasing Difference Pattern
In this number pattern, the terms follow an increasing difference between numbers. To better illustrate this pattern, see the example below:
1, 3, 6, 10, 15, 21, ___
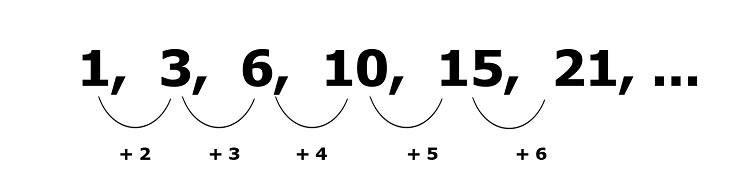
The difference between the numbers increases by 1 as it goes further to the right of the sequence. Based on our illustration above, we can obtain the next term by adding 7 to 21:
21 + 7 = 28
Therefore, the missing term is 28.
Sample Problem 1: Determine the missing term in 15, 19, 24, 30, 37, _______
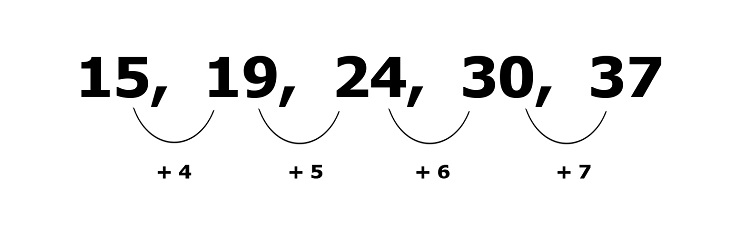
Solution: The difference between the numbers is increasing by 1. Hence, we must add 8 to 37 to get the missing number: 37 + 8 = 45.
Thus, the missing number is 45.
Sample Problem 2: Determine the missing term in 54, 56, 60, 66, 74, ____
Solution: The difference between the numbers is increasing by 2s:
54 + 2 = 56
56 + 4 = 60
60 + 6 = 66
66 + 8 = 74
Hence, the missing term can be calculated by adding 10 to 74:
74 + 10 = 84
Thus, the missing term is 84.
10. Decreasing Difference Pattern
This pattern is the opposite of the previous pattern (the increasing difference pattern). In this number sequence pattern, the difference between the numbers is decreasing.
Sample Problem: Identify the missing term in 29, 26, 21, 14, __________
Solution: The difference between the numbers is decreasing by 2s:
This means that to get the next term; we need to subtract 14 by 9: 14 – 9 = 5.
Therefore, the answer is 5.
Next topic: Data Interpretation
Previous topic: Logic
Return to the main article: Ultimate Logical and Analytical Reasoning Reviewer
Download Article in PDF Format
Test Yourself!
1. Practice Questions [PDF Download]
2. Answer Key [PDF Download]
Jewel Kyle Fabula
Jewel Kyle Fabula is a Bachelor of Science in Economics student at the University of the Philippines Diliman. His passion for learning mathematics developed as he competed in some mathematics competitions during his Junior High School years. He loves cats, playing video games, and listening to music.
Copyright Notice
All materials contained on this site are protected by the Republic of the Philippines copyright law and may not be reproduced, distributed, transmitted, displayed, published, or broadcast without the prior written permission of filipiknow.net or in the case of third party materials, the owner of that content. You may not alter or remove any trademark, copyright, or other notice from copies of the content. Be warned that we have already reported and helped terminate several websites and YouTube channels for blatantly stealing our content. If you wish to use filipiknow.net content for commercial purposes, such as for content syndication, etc., please contact us at legal(at)filipiknow(dot)net
