Two of the most practical things in mathematics are fractions and decimals. Whether you are aware of it or not, you use them daily. You encounter it when shopping, asking for a medical prescription, splitting expenses, following a recipe, paying for transportation, etc. 

This review will discuss everything you need to know about fractions and decimals, including their definitions and other valuable terminologies.

Click below to go to the main reviewers:

Ultimate UPCAT Reviewer

Ultimate NMAT Reviewer

Ultimate Civil Service Exam Reviewer

Ultimate PMA Entrance Exam Reviewer

Ultimate PNP Entrance Exam Reviewer

Ultimate LET Reviewer

Part I: Fractions

What is a fraction?

A fraction is a part or a section of a whole.

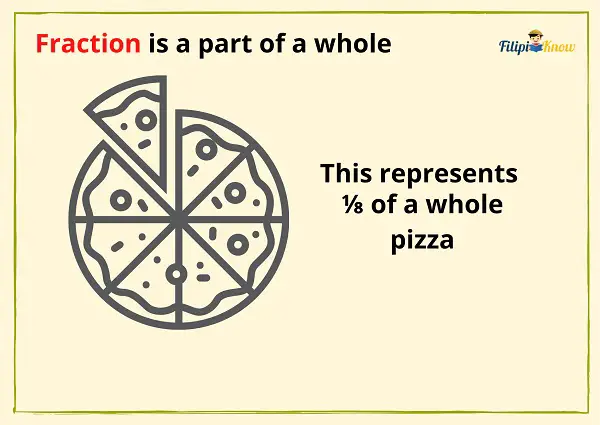
For instance, if you and your friends decide to buy a pizza for a movie marathon, you will cut the pizza into eight slices. You will certainly take one slice from it. That one slice you took is ⅛ of the pizza.

⅛  of the pizza is a fraction since it is a part of the whole (i.e., the entire pizza).

Parts of a Fraction

1. Numerator

A fraction consists of two parts – the numerator and the denominator.

The numerator is the number you see in the upper part of the fraction. It tells you how many sections are represented in the fraction. For example, in ⅛, 1 is the numerator. This means that 1 section of the whole is represented in the fraction.

2. Denominator

On the other hand, the denominator is the number you see in the lower part of the fraction. It tells you how many sections the whole is divided into. For example, in ⅛, 8 is the denominator. This means that the whole is divided into a total of 8 sections.

Illustrating Fractions

Pies are great not only because they are delicious but also because they can be used to represent fractions. Let’s try to illustrate ⅜ using a pie.

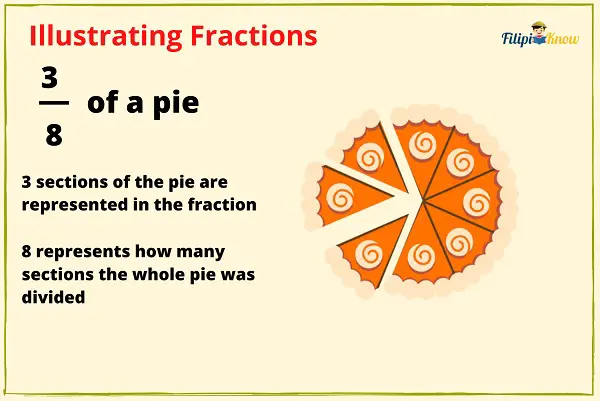
The three slices cut from the pie represent the fraction’s numerator, 3. Meanwhile, the whole pie was divided into eight slices, which means the fraction’s denominator.

There are other ways to represent fractions aside from using a pie. Did you know that your exam scores can illustrate a fraction?

Suppose you have a 50-item exam, and you answered 42 items correctly. Your score can be illustrated as a fraction: 42⁄50, where 42 represents the items of the exam you got correctly while 50 represents the total number of exam items.

Types of Fractions

1. Proper Fractions

A proper fraction is a fraction where the value of the numerator is less than the value of the denominator. For example, ⅝ is a proper fraction since its numerator, which is 5, is less than its denominator, which is 8.

Other examples of proper fractions are ⅓, ⅖, 7⁄9, 121⁄321, and so on. 

2. Improper Fractions

An improper fraction is a fraction where the value of the numerator is greater than or equal to the value of the denominator. For example, 8⁄5 is an improper fraction since its numerator eight is greater than its denominator 5. 

Similarly, 4⁄4 is an improper fraction since its numerator equals the denominator (both are 4). Note that if the numerator and the denominator have the same value, that fraction equals 1. Therefore, 4⁄4= 1.

In other words, when you get a perfect score from a ten-item exam, you have an improper fraction of 10⁄10!

Other examples of improper fractions are 4⁄3, 8⁄5, 120⁄51, 20⁄20, and so on.

Mixed Number

A mixed number combines a whole number and a proper fraction. For example, 2 3⁄4 is a mixed number because it is a combination of a whole number (which is 2) and a proper fraction (which is ¾).

There is an interesting fact about improper fractions and mixed numbers. You can transform an improper fraction into a mixed number and vice-versa. This method is useful when performing some mathematical operations with fractions. Let’s discuss converting an improper fraction to a mixed number below.

1. Converting an Improper Fraction to a Mixed Number Form

Here are the steps you need to follow so you can convert an improper fraction to a mixed number:

1. Divide the numerator by the denominator. To do this, put the numerator inside the division bracket while putting the denominator outside the division bracket, then perform a long division.
2. Designate the quotient as the whole number of the mixed number
3. Assign the remainder as the numerator of the proper fraction part of the mixed number.
4. Copy the denominator of the improper fraction and use it as the denominator of the mixed number.
5. Reduce the proper fraction part of the mixed number, if possible

Example 1: Convert 4⁄3 to mixed number form.

If we can transform an improper fraction into its mixed number form, we can also perform the opposite.

2. Converting a Mixed Number to an Improper Fraction

Here are the steps on how to transform a mixed number into an improper fraction:

1. Multiply the denominator of the mixed number by the whole number part, then add the product to the numerator. The resulting number is the numerator of the improper fraction.
2. Copy the denominator of the proper fraction of the mixed number and use it as the denominator of the improper fraction.
3. Reduce the obtained fraction to its lowest terms, if possible.

Example: Convert 2 3⁄5 to a mixed number.

Therefore, 2 3⁄5 = 13⁄5

Equivalent Fractions

Equivalent fractions are fractions that have equal value. These fractions represent the same portion of the whole. For example, 1⁄2 equals 2⁄4 since they represent the same portion of a whole.

How To Determine an Equivalent Fraction of a Given Fraction

The easiest way to determine an equivalent fraction of a given fraction is to multiply the numerator and the denominator by the same number. 

For example, if we want to find an equivalent fraction of 1⁄2, we can multiply its numerator and denominator by the same number. If we multiply the numerator and the denominator of ½ by 2, we obtain an equivalent fraction of ½, which is 2⁄4.

Example: Find three equivalent fractions of ⅗

To find the answers, multiply the numerator and the denominator of ⅗ with the same numbers thrice.

3⁄5 x 2⁄2 = 6⁄10

                3⁄5 x 3⁄3 = 9⁄15

                 3⁄5 x 4⁄4 = 12⁄20

Therefore, 6⁄10, 9⁄15, and 12⁄20 are equivalent fractions of ⅗. 

How To Determine if Two Fractions Are Equivalent Fractions

One method you can use to determine if two fractions are equivalent is by using the cross-multiplication method.

To perform the cross-multiplication method, follow these steps:

1. Multiply the first fraction’s numerator by the second fraction’s denominator.
2. Multiply the first fraction’s denominator by the second fraction’s numerator.
3. If the products you have obtained from Steps 1 and 2 are equal, then the fractions are equivalent. Otherwise, the fractions are not equivalent.

Let us try these steps in our next example.

Example: Are ¼ and 3⁄12 equivalent fractions?

Use the cross-multiplication method:

1. Multiply the first fraction’s numerator by the second fraction’s denominator.

1 x 12 = 12

2. Multiply the first fraction’s denominator by the second fraction’s numerator.

           4 x 3 = 12

3. If the products you have obtained from Steps 1 and 2 are equal, then the fractions are equivalent.

We have obtained 12 both from Step 1 and Step 2. Hence, ¼ and 3⁄12 are equivalent fractions.

Fractions in Lowest Terms

A fraction is in its lowest terms if the numerator and the denominator of a fraction have no common factor other than 1. In other words, the fraction’s numerator and denominator are prime numbers.

The lowest term of a fraction is also known as its “simplest form.”

For example, ⅔ is a fraction in the lowest terms because its numerator and denominator have no common factor other than 1. Also, both 2 and 3 are prime numbers.

On the other hand, 15⁄20 is not the lowest term because its numerator (15) and denominator (20) have a common factor of 5. 

How To Reduce a Fraction to Its Lowest Term

Reducing or simplifying a fraction to its lowest term transforms it into its simplest form.

For example, 15⁄20 is a fraction not in its lowest term. We can transform 15⁄20 into an equivalent fraction in the lowest term. The lowest term of 15⁄20 is 3⁄4. We will discuss in the next section how to reduce a fraction into its lowest terms.

It is important to note that the original fraction and its lowest term are equivalent fractions. Therefore, 15⁄20 and its simplified form, 3⁄4, are equivalent fractions.

Finding the Lowest Terms of a Fraction Using the Greatest Common Factor (GCF)

The most reliable way to transform a fraction into its lowest term is using the Greatest Common Factor (GCF) of the numerator and the denominator. To convert a given fraction to its lowest terms:

1. Determine the GCF of the numerator and the denominator.
2. Divide the numerator and the denominator by the GCF; the resulting fraction is reduced into the lowest terms.

Example 1: What is 8⁄10 in its lowest terms?

1. Determine the GCF of the numerator and the denominator.

Determine the GCF of 8 and 10. Using the prime factorization method, the GCF of 8 and 10 is 2.

2. Divide the numerator and the denominator by the GCF.

8⁄10 ÷ 2⁄2 = 4⁄5

The resulting fraction is ⅘. Hence, ⅘ is the lowest term of 8⁄10. 

Example 2: Simplify 45⁄225.

1. Determine the GCF of the numerator and the denominator.

Determine the GCF of 45 and 225. Using the prime factorization method, the GCF of 45 and 225 is 45.

2. Divide the numerator and the denominator by the GCF.

45⁄225 ÷ 45⁄45 = 1⁄5

The resulting fraction is ⅕. Hence, ⅕  is the lowest term of 45⁄225.  

Similar and Dissimilar Fractions

Similar fractions are fractions with the same denominators. For example, 2⁄3 and 1⁄3 are similar fractions since their denominators are the same (3).

Dissimilar fractions are fractions whose denominators aren’t the same. For example, 2⁄5 and 1⁄3 are dissimilar fractions since their denominators differ.

Dissimilar fractions can be transformed into equivalent fractions using the Least Common Multiple.

Part II: Decimals

Just like fractions, decimals are also a practical tool in mathematics. We encounter them in money, length, weight, time, etc. The most obvious characteristic of a decimal number is that it has a decimal point. 

However, what is a decimal number?

What Are Decimals?

Decimals are numbers that combine a whole number and a fraction. A decimal point separates the whole number part from the fractional part (.). 

The numbers on the left of the decimal point are the whole number, while the numbers on the right of the decimal point are the decimal numbers that represent the fractional part.

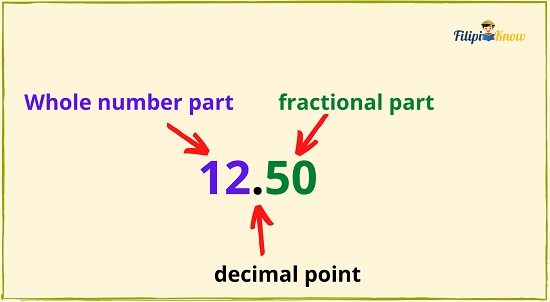
Suppose you buy a pencil that costs PHP 12.50.

12.50 is a decimal number where 12 is the whole number part while 50 is the fractional part.

Place Value of Decimal Numbers

Just like whole numbers, decimal numbers also have corresponding place values. However, the world of decimal numbers differs from that of whole numbers.

Let’s use the decimal number 18.945 as an example.

We know that 18 is the whole number part of the decimal number. We also know the corresponding place value of the digits 18; 8 is in the ones digit, while one is in the tens digit. However, once we step to the right of the decimal point, we will encounter a new system for the place values of the digits of the decimal number.

The first digit on the right of the decimal point is the digit in the tenths place. Hence, 9 is in tenths place. Its value is 0.9.

The second digit on the right of the decimal point is the digit in the hundredths place. Hence, 4 is in the hundredths place. Its value is 0.04

The third digit on the right of the decimal point is the digit in the thousandths place. Hence, 5 is in the thousandths place. Its value is 0.005.

As you move to the left of the decimal number, the place value of the digits becomes ten times larger. Therefore, the tenths place is 10 times larger than the hundredths place; the hundredths place is ten times larger than the thousandths place, and so on.

Types of Decimal Numbers

You will encounter a lot of decimal numbers in your study of different branches of mathematics. However, you can only classify them into four types:

1. Terminating Decimals

These are the decimal numbers where the digits of the fractional part are finite or have an end. This means that the digits after the decimal point are countable. Terminating decimals are also known as exact decimals.

Some examples of terminating decimals are 0.5, 0.82, 0.3113, -0.4531, and so on. Note that the numbers at the right of these decimal numbers are countable or finite.

2. Non-terminating Decimals

These are the opposite of terminating decimals. The number of digits on the right of the decimal point is infinite or has no end. This means that the digits after the decimal point are uncountable.

Some examples of non-terminating decimals are 0.123533124464…, 0.23134823…, 0.5123…, and so on.

Recall that non-terminating decimal numbers are irrational, and we cannot express them as fractions with integers.

3. Terminating and Repeating (Recurring) Decimal Numbers

These are terminating decimal numbers where the digits on the right of the decimal point are repeating but have an end. As long as the number of digits in the fractional part is countable, the decimal number is a terminating and repeating decimal number.

 Examples are 0.4242, 0.152152152, 0.101101101, and so on. 

4. Non-terminating and Repeating (Recurring) Decimal Numbers

These are non-terminating decimal numbers where the digits on the right of the decimal point are repeating but have no end. As long as the number of digits in the fractional part is uncountable, the decimal is a non-terminating and repeating decimal number.

Examples are 0.25252525…, 0.727272…, 0.818181…, 0.543254325432…, and so on.

How To Convert Fractions into Decimals

If you have half (½) of a peso, you have 0.5 pesos. Therefore, ½ is equivalent to 0.5. However, how am I able to convert ½ into 0.5? How did I convert a fraction into its decimal form?

The easiest way to convert fractions into their decimal form is, of course, by using a calculator. However, knowing how to manually convert fractions into their decimal form gives you an edge during an examination where calculators are not allowed.

Let us discuss manually converting a proper fraction into its decimal form.

1. Converting a Proper Fraction to its Decimal Form

Here are the steps to convert a proper fraction into its decimal form:

1. Divide the numerator by the denominator. Use the numerator as the dividend while the denominator as the divisor.
2. Put a zero with a decimal point above the division bracket, then add a decimal point and a zero after the number inside the division bracket.
3. Apply long division.

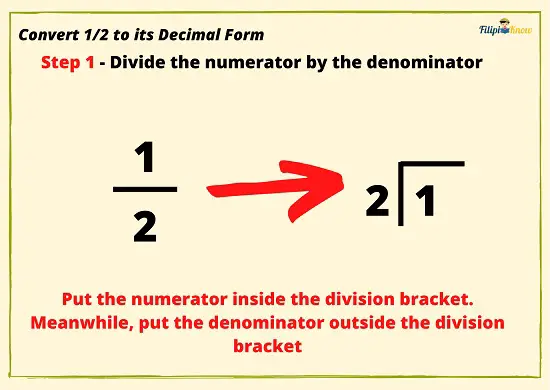
Example 1: Convert ½  to its decimal form.

Step 1: Divide the numerator by the denominator. Use the numerator as the dividend while the denominator as the divisor.

We put 1 inside the division bracket since it is the fraction’s numerator. Meanwhile, we put 2 outside the division bracket since it is the fraction’s denominator.

Step 2: Put a zero with a decimal point above the division bracket, then add a decimal point and a zero after the number inside the division bracket.

As we add a decimal point and a zero to the number inside the division bracket, 1 becomes 10. We can divide 10 by 2 and proceed with the usual division process.

Step 3: Apply long division.

We may now perform division with whole numbers:

Therefore, the decimal form of ½  is 0.5

Example 2: Convert ⅓ to its decimal form.

Step 1: Divide the numerator by the denominator. Use the numerator as the dividend while the denominator as the divisor.

We put 1 inside the division bracket since it is the fraction’s numerator. Meanwhile, we put 3 outside the division bracket since it is the fraction’s denominator.

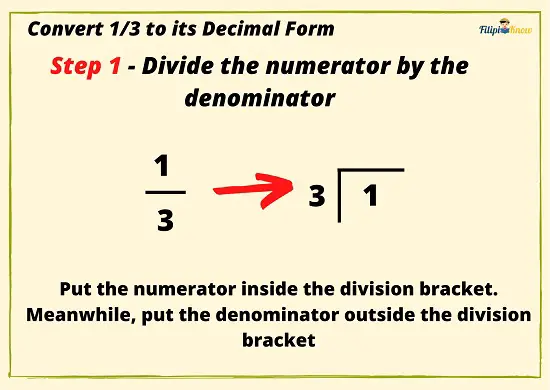
Step 2: Put a zero with a decimal point above the division bracket, then add a decimal point and a zero after the number inside the division bracket.

Step 3: Apply long division.

Continue adding 0 to the remainder if it is smaller than the divisor so you can continue the division process.

Since the division process is never-ending and we will never arrive at a remainder of 0, then the decimal form of the fraction is a non-terminating decimal. Furthermore, since the digits of the decimal are repeating or recurring, it means that the decimal number we obtained is a non-terminating and repeating decimal.

Therefore, the decimal form of ⅓ is 0.333… 

What if the given fraction is improper and the numerator is greater than the denominator? Let’s discuss the steps below.

2. Converting an Improper Fraction to its Decimal Form

Here are the steps to convert an improper fraction into its decimal form:

1. Divide the numerator by the denominator. Use the numerator as the dividend while the denominator as the divisor.
2. Divide the whole numbers.
3. If there’s a remainder, add a decimal point and a zero to the right of the number inside the division bracket and add a zero also to the right of the remainder.
4. Apply long division and put a decimal point to the final answer.

Example: Convert 8⁄5 to its decimal form.

1. Divide the numerator by the denominator. Use the numerator as the dividend while the denominator as the divisor.

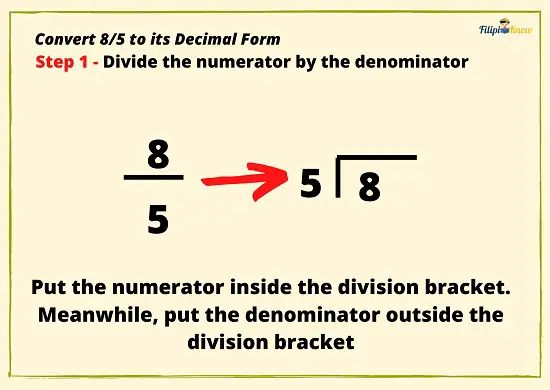
2. Divide the whole numbers.

3. If there’s a remainder, add a decimal point and a zero to the right of the number inside the division bracket and add a zero also to the right of the remainder.

4. Apply long division and put a decimal point to the final answer.

3. Converting a Mixed Number to its Decimal Form

There are only two steps you must keep in your mind so you will be able to convert a mixed number to its decimal form:

1. Use the whole number part of the mixed number as the whole number part of the decimal form
2. Convert the proper fraction part of the mixed number into its decimal form. The obtained result is the fractional part of the decimal form.

Example: Convert 2 2⁄5 to its decimal form.

1. Use the whole number part of the mixed number as the whole number part of the decimal form.

The whole number part in 2 2⁄5 is 2. Therefore, this is also the whole number part of its decimal form.

2. Convert the proper fraction part of the mixed number into its decimal form. The obtained result is the fractional part of the decimal form.

Using the steps on converting a proper fraction into its decimal form (you can review the steps in the section above), ⅖ is equal to 0.4.

Therefore, the decimal form of 2 2⁄5 is 2.4

How To Convert Decimals into Fractions

If we can convert fractions into decimals, we can also perform the opposite. We can convert a decimal into a fraction form.

However, take note that not all decimals can be converted into fractions. Again, non-terminating decimals are irrational numbers, meaning they cannot be expressed as fractions.

Let’s now proceed to the steps on how to convert decimals into fractions:

1. Use the numbers on the right of the decimal point as the fraction’s numerator. Do not write the zeros immediately after the decimal point and before the nonzero digit.
2. If there is one digit on the right of the decimal point, use 10 as the denominator. If there are two digits on the right of the decimal point, use 100 as the denominator. If there are three digits on the right of the decimal point, use 1000 as the denominator.
3. Reduce the fraction you have obtained from Step 1 and Step 2 into its lowest terms.

Example 1: Convert 0.2 to its fraction form.

1. Use the numbers on the right of the decimal point as the fraction’s numerator. Do not write the zeros immediately after the decimal point and before the nonzero digit.

The number on the right of the decimal point is 2. Therefore, the numerator of the fraction form is 2.

2. If there is one digit on the right of the decimal point, use 10 as the denominator. If there are two digits on the right of the decimal point, use 100 as the denominator. If there are three digits on the right of the decimal point, use 1000 as the denominator.

Since there’s only one digit on the right of the decimal point (2), we will use 10 as the denominator. This means that we have 2⁄10.

3. Reduce the fraction you have obtained from Step 1 and Step 2 into its lowest terms.

The Greatest Common Factor (GCF) of 2 and 10 is 2. Dividing both the numerator and the denominator of 2⁄10 by 2:

2⁄10 ÷ 2⁄2 = 1⁄5

Therefore, the fraction form of 0.2 is ⅕ 

Example 2: Convert 0.008 to a fraction.

1. Use the numbers on the right of the decimal point as the fraction’s numerator. Do not write the zeros immediately after the decimal point and before the nonzero digit.

The number on the right of the decimal point is 008. However, we will not consider those numbers on the left of 8 because they immediately appear after the decimal point and before the nonzero digit. This means that the numerator of our fraction is 8.

2. If one digit is on the right of the decimal point, use 10 as the denominator. If there are two digits on the right of the decimal point, use 100 as the denominator. If there are three digits on the right of the decimal point, use 1000 as the denominator, and so on.

There are three digits on the right of the decimal point (i.e., 008). Hence, we will use 1000 as the denominator. This means we have 8⁄1000.

3. Reduce the fraction you have obtained from Step 1 and Step 2 into its lowest terms.

The Greatest Common Factor (GCF) of 8 and 1000 is 8. Dividing both the numerator and the denominator of 8⁄1000 by 8:

8⁄1000 ÷ 8⁄8 = 1⁄125

Therefore, 0.008 is equal to 1⁄125

Next topic: Operations on Fractions and Decimals

Previous topic: Divisibility Rules

Return to the main article: The Ultimate Basic Math Reviewer

Download Printable Summary/Review Notes

Download Printable Flashcards

Test Yourself!

1. Practice Questions [Free PDF Download]

2. Answer Key [Free PDF Download]

3. Math Mock Exam + Answer Key