The four fundamental operations are the heart of arithmetic.

If we can perform these mathematical operations with integers, we can also perform them on fractions and decimals. Many real-life world problems that whole numbers cannot address can be answered using the operations of these rational numbers.

This review gives you the most comprehensive guide to performing the four fundamental operations on fractions and decimals. Most importantly, you’ll also learn how they can be applied to solve real-life word problems. 

Click below to go to the main reviewers:

Ultimate UPCAT Reviewer

Ultimate NMAT Reviewer

Ultimate Civil Service Exam Reviewer

Ultimate PMA Entrance Exam Reviewer

Ultimate PNP Entrance Exam Reviewer

Ultimate LET Reviewer

Part I: Operations on Fractions

Addition and Subtraction of Similar Fractions

As you can recall, similar fractions have the same denominator. The rules for adding and subtracting similar fractions are the same. To add or subtract similar fractions, follow these steps:

1. Add or subtract the numerators of the given fractions and use the sum or difference as the numerator of the resulting fraction.
2. Copy the denominator of the given fractions and use it as the denominator of the resulting fraction.
3. Reduce the answer to its lowest terms, if possible.

To summarize: To add or subtract similar fractions, you first need to add or subtract the numerator, then copy the denominator. Afterward, simplify your answer to its lowest terms.

Example 1: ⅗ + ⅕.

Solution:

Step 1: Add the numerators of the given fractions and use the sum or difference as the numerator of the resulting fraction.

We add the numerators of the given fractions (i.e., 3 and 1) and put the answer as the numerator of the resulting fraction.

Step 2: Copy the denominator of the given fractions and use it as the denominator of the resulting fraction.

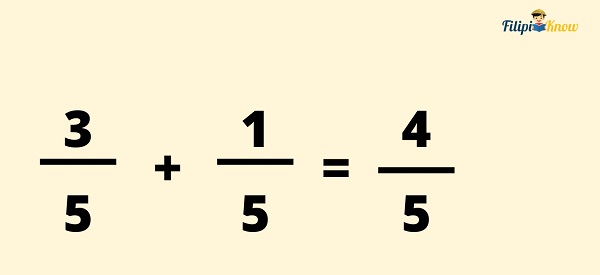
The denominator of the given fractions is 5. Hence, we will use 5 as the denominator of the common fraction.

Step 3: Reduce the answer to its lowest terms, if possible.

⅘ is a fraction in the lowest terms. Hence, no need to simplify it further. Therefore, our final answer is ⅘.

Let’s try to answer more examples:

Example 2: Add ¼ and 2/4.

Solution: 

Example 3: Subtract 3⁄21 from 10⁄21.

Solution:

Note that the problem asked us to subtract 3⁄21 from 10⁄21. This means that the minuend (the number being subtracted from) is 10⁄21 while the subtrahend (the number being subtracted) is 3⁄21.

Example 4: Bea ate 2⁄8 of the pie that her mother prepared. Meanwhile, Bea’s brother ate 4⁄8 of the same pie that Bea ate. What is the total fraction of the pie eaten by Bea and her brother?

Solution: 

We can answer this question by adding the fraction of the pie eaten by Bea and the fraction of the pie eaten by her brother. Since 2⁄8 and 4⁄8 are similar fractions, we can use our steps for adding similar fractions.

Step 1: Add the numerators of the given fractions and use the sum as the numerator of the resulting fraction.

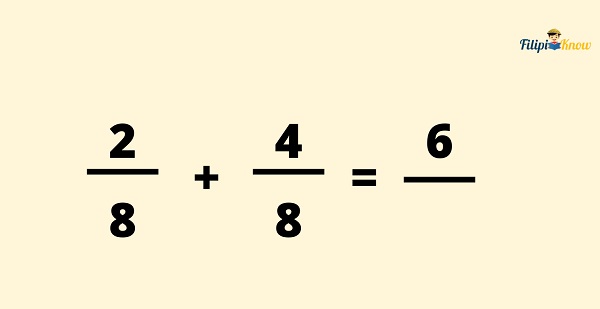
Step 2: Copy the denominator of the given fractions and use it as the denominator of the resulting fraction.

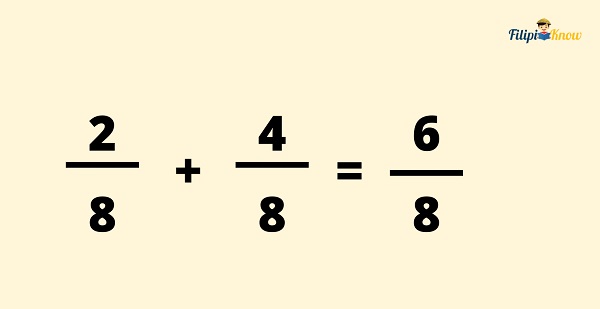
Step 3: Reduce the answer to its lowest terms, if possible.

6⁄8 is not in its lowest terms yet since 6 and 8 have a Greatest Common Factor (GCF) of 2. Hence, we divide both 6 and 8 by 2.

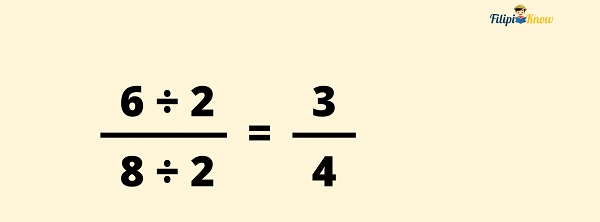
Therefore, Bea and her brother ate 6⁄8 or ¾ of the pie.

Transforming Dissimilar Fractions to Similar Fractions

Do you still remember what dissimilar fractions are? These are fractions with different denominators. Before adding or subtracting dissimilar fractions, you should transform them into similar fractions. But how is that possible?

These are the steps on how to transform dissimilar fractions into similar fractions:

1. Find the Least Common Multiple (LCM) of the denominators. The number that you will obtain is the Least Common Denominator (LCD). Use the LCD as the new denominator of the fractions.
2. Divide the LCM you have obtained by the denominator of the first fraction. Multiply the resulting number by the numerator. The number that you will get is the numerator for the new fraction. 
3. Apply Step 2 for the second fraction.

Example: Transform the fractions ⅗ and ⅓ into similar fractions.

Solution:

Let us apply all the steps previously discussed.

Step 1: Find the denominators’ Least Common Multiple (LCM). The number that you will obtain is the Least Common Denominator (LCD). Use the LCD as the new denominator of the fractions.

The Least Common Multiple of 5 and 3 is 15 (we colored it purple in the list). 15 will be our Least Common Denominator (LCD).

We will use 15 as the denominator of our fractions. We leave the numerators of the fractions blank because we need to compute them in the next step.

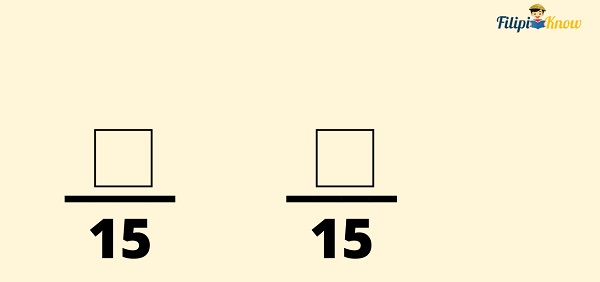
Step 2: Divide the LCM you obtained by the first fraction’s denominator. Multiply the resulting number by the numerator. The number that you will obtain is the numerator for the new fraction.

Let us apply this step to ⅗.

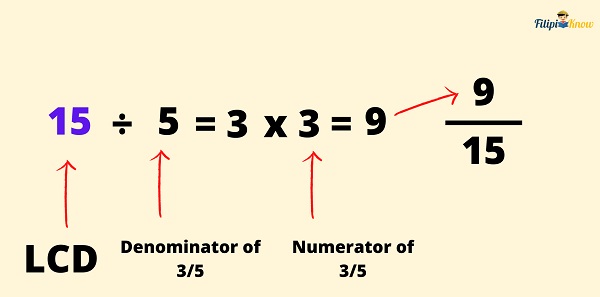
The LCD we have obtained is 15. We divide the LCD by the denominator of ⅗. Thus, 15 ÷ 5 = 3. Afterward, we multiply 3 by the numerator of ⅗. Hence, 3 x 3 = 9. Therefore, the new numerator is 9. 

Step 3: Apply Step 2 for the second fraction.

We will do the same thing we performed on ⅗ for the second fraction, which is ⅓. We divide the LCD of 15 by the denominator of ⅓, which is 3. Thus, 15 ÷ 3 = 5. Afterward, we multiply 5 by the numerator of ⅓. Hence, 5 x 1 = 5. The new numerator for the second fraction is 5.

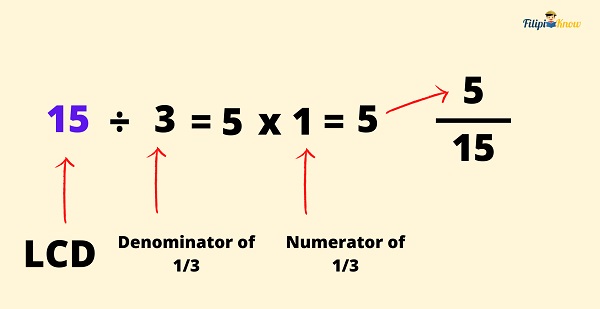
When we transform the fractions ⅗ and ⅓ into similar fractions, we have 9⁄15 and 5⁄15.

Transforming dissimilar fractions into similar fractions is essential in adding and subtracting dissimilar fractions. This means you should master the method presented above before proceeding to the next section of this review.

Addition and Subtraction of Dissimilar Fractions

Here are the steps on how to add or subtract dissimilar fractions:

1. Change the given dissimilar fractions into similar fractions (refer to the section above for the steps on transforming dissimilar fractions to similar fractions).
2. Proceed with the steps on addition or subtraction of similar fractions.
3. Reduce the resulting fraction to its lowest terms, if possible.

Let us try the steps above for the examples below.

Example 1: What is the sum of ⅑ and ⅔?

Solution:

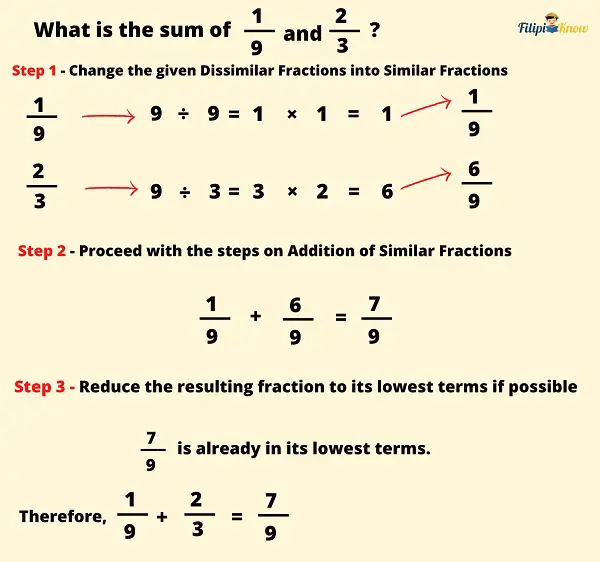
The LCD of 3 and 9 is 9. Hence, we used it as the new denominator of our fractions. Afterward, we performed the steps for changing dissimilar fractions into similar fractions. In Step 2, we just added the numerators: 1 + 6 = 7 and copied the denominator 9. Thus, we obtained a fraction of 7⁄9.

7⁄9 is already in its lowest terms, so there is no need to simplify it further. Hence, the final answer is 7⁄9.

Example 2: Compute for ⅓ – ¼.

Solution:

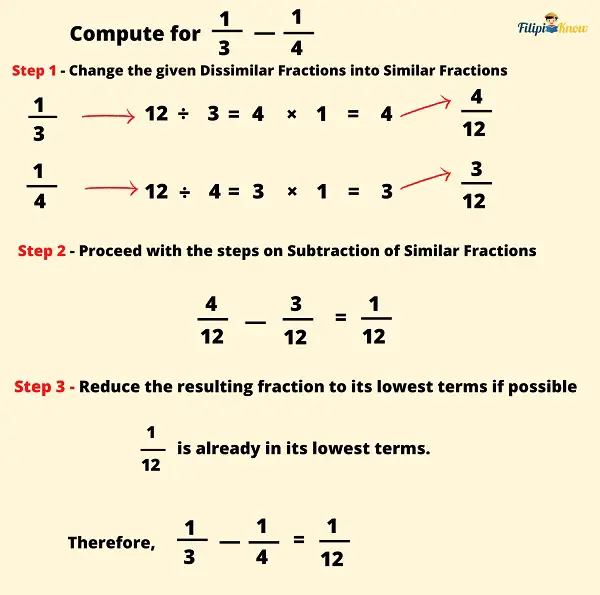
The LCD of 3 and 4 is 12. Thus, we used it as the new denominator of the fractions. Afterward, we applied the steps for transforming dissimilar fractions into similar fractions. Therefore, we obtained 4⁄12 and 3⁄12. In Step 2, we subtracted the numerators: 4 – 3 = 1 and then copied the denominator 12. Thus, we obtained a fraction of 1⁄12.

Since 1⁄12 is already in its lowest terms, there is no need to simplify it further. Therefore, the final answer is 1⁄12.

Addition and Subtraction of Mixed Numbers

You are now familiar with adding and subtracting similar or dissimilar fractions. How about mixed numbers or those combinations of a whole number and a proper fraction? Can we also add or subtract them? Of course, we can.

Here are the steps you need to follow if you are adding or subtracting mixed numbers:

1. Add or subtract the whole numbers. The resulting number is the whole number part of the sum or difference.
2. Add or subtract the proper fractions. If the given fractions are similar, add or subtract the numerators, then copy the denominator. If the given fractions are dissimilar, make the fractions similar first.
3. Combine the whole number you obtained from Step 1 and the proper fraction from Step 2 to arrive at a mixed number.
4. Reduce the proper fraction to its lowest terms, if possible.

Example: Add 1⅓ and 4⅖.

Solution: 

Step 1: Add the whole numbers. The resulting number is the whole number part of the sum.

The whole number parts of 1⅓ and 4⅖ are 1 and 4, respectively. Adding the whole numbers:

1 + 4 = 5

Therefore, 5 is the whole number part of our sum.

Step 2: Add the proper fractions. If the given fractions are similar, add the numerators, then copy the denominator. If the given fractions are dissimilar, make the fractions similar first.

The proper fractions of 1⅓ and 4⅖ are ⅓ and ⅖, respectively. These proper fractions are dissimilar,, so we must first transform them into similar fractions.

If we transform ⅓ and ⅖ into similar fractions, we will have (refer to our previous section to review how to transform dissimilar fractions into similar fractions):

⅓ → 5⁄15

⅖ → 6⁄15

Now, we add similar fractions: 

5⁄15 + 6⁄15 = 11⁄15

Step 3: Combine the whole number you obtained from Step 1 and the proper fraction you got from Step 2 to arrive at a mixed number.

The whole number that we have obtained from Step 1 is 5. Meanwhile, the proper fraction we have obtained from Step 2 is 11⁄15. Combining them, we have 5 11⁄15.

Step 4: If possible, reduce the proper fraction to its lowest terms.

Since 11⁄15 is in its lowest terms, we do not need to simplify it.

Therefore, 1⅓ + 4⅖ = 5 11⁄15.

Multiplication of Fractions

Multiplying fractions is much easier than adding or subtracting fractions because you do not have to consider whether the fractions are similar or dissimilar. To multiply fractions, all you have to do is follow these three steps:

1. Multiply the numerators of the given fractions. The resulting number is the numerator of the product (or answer).
2. Multiply the denominators of the given fractions. The resulting number is the denominator of the product (or answer).
3. If possible, reduce the product (or answer) to its lowest terms.

We can summarize these three steps this way: Multiply numerator by numerator and then denominator by denominator. Afterward, reduce the product to its lowest terms.

Example 1: Multiply ¾ by ⅕.

Solution:

Step 1: Multiply the numerators of the given fractions. The resulting number is the numerator of the product (or answer).

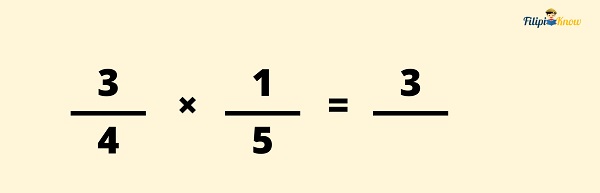
The numerators of the given fractions are 3 and 1. When we multiply them, we will obtain 3 x 1 = 3. Hence, 3 is the numerator of our resulting fraction.

Step 2: Multiply the denominators of the given fractions. The resulting number is the denominator of the product (or answer).

Step 3: If possible, reduce the product (or answer) to its lowest terms.

3⁄20 is a fraction that is already in the lowest terms. Hence, no need to simplify it further.

Therefore, our final answer is 3⁄20.

Let us have more examples:

Example 2: Multiply 5⁄9 by 2⁄4.

Solution:

Therefore, the product is 5⁄18.

Example 3: What is ⅖ of 50?

Solution:

The word “of” is a signal word for the multiplication of fractions. Hence, the question above can also be interpreted as ⅖ × 50.

But how do we multiply a fraction by a whole number or vice versa?

The answer is simple! Just put a denominator of 1 for the whole number:

⅖ × 50⁄1

Afterward, proceed with the steps on multiplying fractions.

⅖ × 50⁄1 = 100⁄5

Note that we can simplify 100⁄5 as 20⁄1.

If the denominator of a fraction is 1, it means that the fraction is equal to the whole number indicated in the numerator.

Therefore, 20⁄1 = 20

Hence, ⅖ of 50 is equal to 20.

Example 4: What is ¾ of 100?

Solution:

This question can be solved using the same method we used for the previous example. Again, the word “of” is a signal word for multiplying fractions.

Let us start by putting a denominator of 1 for 100:

¾ × 100⁄1

Multiply the numerators as well as the denominators:

           ¾ × 100⁄1 = 300⁄4

We can simplify 300⁄4 as 75⁄1, which is equal to 75.

Hence, ¾ of 100 is equal to 75.

Multiplying Fractions Through Cancellation Method.

We can make the process of multiplying fractions quicker through the cancellation method. In this method, we “cancel” numbers with common factors so we can arrive at the product already in its lowest terms.

Example 1: Multiply 4⁄20 by ⅝.

Solution:

Using the cancellation method, the answer is 1⁄8.

Example 2: What is 3⁄7 of 49?

Solution:

Again, the word “of” is a signal word for multiplying fractions.

Therefore, 3⁄7 of 49 is equal to 21.

Division of Fractions

We are now on the fourth mathematical operation on fractions – division. However, before we proceed to the actual process of dividing fractions, let me introduce you first to the concept of the reciprocal or multiplicative inverse of a number.

Reciprocal or Multiplicative Inverse of a Number

The reciprocal or multiplicative inverse of a fraction is the fraction that, when multiplied by the original fraction, the result is 1. This definition sounds confusing and too technical, so let me provide you with an easier way to grasp this concept.

Let’s use the fraction ⅚ as an example. The reciprocal of this fraction can be obtained by interchanging the positions of the numerator and the denominator. Therefore, the reciprocal of ⅚ is simply 6⁄5.

Easy, right? Now, can you determine the reciprocal of the following:

⅘, ⅝, and 25.

Here are the answers:

The reciprocal of ⅘ is 5⁄4.

The reciprocal of ⅝ is 8⁄5.

Meanwhile, the reciprocal of 25 is 25⁄1.

Let us go back to the definition of the reciprocal. The reciprocal or multiplicative inverse of a fraction is the fraction that, when multiplied by the original fraction, the result is 1. This means that when you multiply a fraction by its reciprocal, the result is 1. For instance, when you multiply ⅘ by 5⁄4, you will obtain 1.

Now that you know what the reciprocal is, you are prepared to proceed with the steps to divide fractions.

How To Divide Fractions

Here are the steps you need to follow so you will be able to divide fractions:

1. Transform the second fraction (the divisor) into its reciprocal (turn the fraction upside down).
2. Multiply the first fraction by the reciprocal of the second fraction.
3. Reduce the obtained fraction to its lowest terms, if possible.

Example 1: What is ⅚ divided by 6⁄4?

Solution:

Therefore, ⅚ ÷ 6⁄4 = 5⁄9

Example 2: Divide 3⁄7 by ½.

Solution:

Step 1: Transform the second fraction (the divisor) into its reciprocal (turn the fraction upside down).

The second fraction (the divisor) is ½. Its reciprocal is 2⁄1.

Step 2: Multiply the first fraction by the reciprocal of the second fraction.

3⁄7 × 2⁄1 = 6⁄7

Step 3: If possible, reduce the obtained fraction to its lowest terms.

6⁄7 is already in its lowest terms. Hence, we do not need to simplify it.

Therefore, 3⁄7 ÷ ½ = 6⁄7

Multiplication and Division of Mixed Numbers

You already learned how to perform multiplication and division on fractions. This time, let us discuss how to perform the same operations with mixed numbers.

When multiplying or dividing mixed numbers, you first have to transform the given mixed numbers into improper fractions. Afterward, proceed with the steps on multiplying or dividing fractions. 

Therefore, I suggest you review the steps on how to transform mixed numbers into improper fractions so you can multiply or divide mixed numbers with ease.

Let’s have some examples:

Example 1:  Multiply 1⅔ by ⅖.

Solution:

The first thing you have to do is to transform the given mixed number into an improper fraction.

1⅔ is a mixed number. If you transform it into an improper fraction, you have 5⁄3.

Afterward, you may now proceed with multiplying 5⁄3 by ⅖.

Lastly, we can reduce 10⁄15 to its lowest terms:

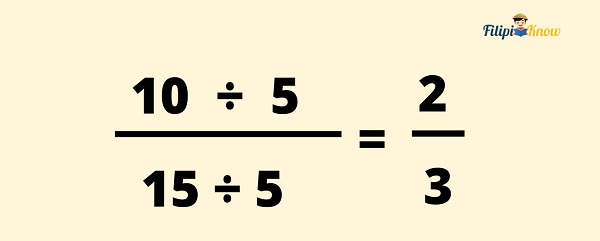
Therefore, 1⅔ × 2⁄5 = ⅔

Example 2: Divide 8⅗ by 9.

Solution: 

Start by transforming the given mixed number into an improper fraction.

8⅗ = 43⁄5

Now, let’s proceed to divide 43⁄5 by 9. The reciprocal of  9 is ⅑.

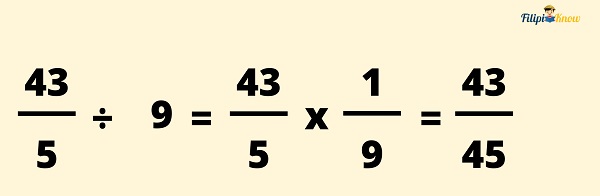
Therefore, 8⅗ ÷ 9 = 43⁄45 

Part II: Operations on Decimals

If we can add, subtract, multiply, and divide fractions, we can perform these operations with decimal numbers. In this section, let’s discuss how to perform these mathematical operations with decimals.

Addition and Subtraction of Decimals

To add decimal numbers, follow these steps:

1. Align the decimal numbers vertically, with the decimal points lined up.
2. Add zeros at the end of some decimal numbers so the decimals will be the same length.
3. Add or subtract the digits and put the decimal point in the final answer.

Example 1: Delly bought a pencil worth ₱8.25 and an eraser worth ₱4.105. How much is the total amount of items that Delly bought?

Solution: We can answer this problem by adding the given amounts, decimal numbers.

To solve this problem, we started by aligning the given decimal numbers. Afterward, we added a zero at the end of 8.25 so that it would be the same length as 4.105. Lastly, we performed column addition from right to left (just like with whole numbers) and put the decimal point by bringing it down.

Therefore, 8.25 + 4.105 = 12.355

Example 2: Letty loves jogging. On Monday, she jogged a distance of 3.258 km. Meanwhile, on Tuesday, she jogged a distance of 4.15 km. What is the total distance covered by Letty on Monday and Tuesday?

Solution: 

We can answer this problem by adding the given distances, decimal numbers.

Therefore, Letty covered a total distance of 7. 408 km on Monday and Tuesday.

Example 3: Berto has 2.598 liters of alcohol. He used 0.52 liters to disinfect his furniture. How many liters of alcohol were left?

Solution:

We can solve this problem by subtracting 0.52 from 2.598

Therefore, 2.078 liters of alcohol were left.

Example 4: What is the difference between 9.453 and 7.38?

Solution:

Thus, the difference between 9.453 and 7.38 is 2.073.

Multiplication of Decimals

When multiplying decimal numbers, you first have to ignore the decimal point and multiply the digits just like whole numbers. Then, put the decimal point in the answer.  The resulting number must have as many decimal places as the number of decimal places the original decimals have. 

To understand the method mentioned above, let us have some examples:

Example 1: Multiply 5.45 by 1.2

Solution:

We start our calculation by ignoring the decimal point and multiplying the numbers like whole numbers.

We have obtained 6540 from Step 1, but it is not the final answer yet. We need to put the decimal point somewhere in its digits. 

5.45 has two digits at the right of its decimal point. Thus, it has two decimal places. Meanwhile, 1.2 has one digit at the right of its decimal point. Therefore, it has one decimal place. The total number of decimal places we now have is three (two from 5.45 and one from 1.2). Thus, the final answer must have three decimal places.

To determine where we should put our decimal point in 6540, count three digits from the right, then put the decimal point. Hence, the decimal point should be at 6.540

Thus, the answer is 6.540 or 6.54

Division of Decimals

To divide decimal numbers, you may follow these steps:

1. Move the decimal point of the divisor (the second decimal) to the right until it becomes a whole number.
2. Move the decimal point in the dividend (the first decimal) to the right in the same places you move the decimal point in the divisor.
3. Divide normally just like whole numbers using the new decimals obtained from Steps 1 and 2 and put the decimal point to the final answer.

Let us apply these steps to our example below:

Example: Divide 32.95 by 0.5

Solution: 

Step 1: Move the decimal point of the divisor (the second decimal) to the right until it becomes a whole number.

We can move one decimal place to the right of 0.5 so that it becomes a whole number (which is 5). 

Step 2: Move the decimal point in the dividend (the first decimal) to the right in the same number of places you move the decimal point in the divisor.

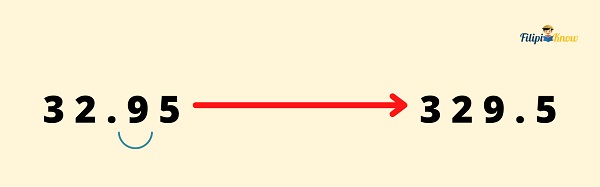
Step 3: Divide normally like whole numbers using the new decimals obtained from Steps 1 and 2 and put the decimal point to the final answer.

Therefore, 32.95 ÷ 0.5 = 65.9

Next topic: Percentage

Previous topic: Fractions and Decimals

Return to the main article: The Ultimate Basic Math Reviewer

Download Printable Summary/Review Notes

Download Printable Flashcards

Test Yourself!

1. Practice Questions [Free PDF Download]

2. Answer Key [Free PDF Download]

3. Math Mock Exam + Answer Key