You have learned what integers are and how they fit in the number family tree. Now, it’s time to go to the next level and learn how to apply fundamental operations on integers.

In this review, you’ll learn how to add, subtract, multiply, and divide integers.

Click below to go to the main reviewers:

Ultimate UPCAT Reviewer

Ultimate NMAT Reviewer

Ultimate Civil Service Exam Reviewer

Ultimate PMA Entrance Exam Reviewer

Ultimate PNP Entrance Exam Reviewer

Ultimate LET Reviewer

Absolute Value of a Number

Before we proceed to our actual topic, we need to discuss first the concept of absolute value.

The absolute value of a number is its distance from zero. In other words, the absolute value of a number tells you how far a number from zero is. We use the symbol | | to indicate the absolute value of a number.

Example 1: What is the absolute value of 3?

Solution: Let’s determine how far three is from zero.

Using a number line, you can verify that 3 is three units far from zero.

Therefore, the absolute value of 3 is equal to 3. 

In symbols, | 3 | = 3.

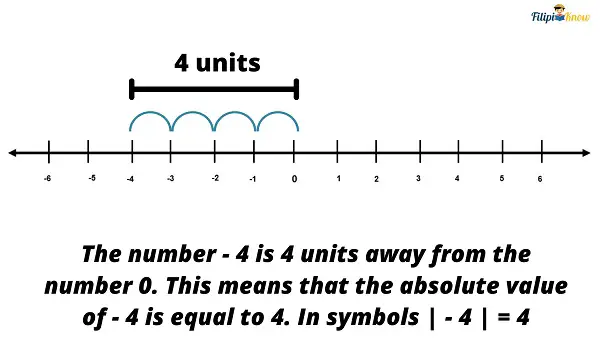
Example 2: What is the absolute value of – 4?

Solution: Using a number line, you can verify that – 4 is four units away from zero. 

Hence, the absolute value of -4 is equal to 4.

In symbols, | – 4 | = 4

It is important to note that the absolute value of a number is always nonnegative (either positive or 0) since we are dealing with the distance of a number from zero which is always non-negative. You will never encounter a negative value for distance. There’s no such road that is – 60 km long.

Finding the Absolute Value of a Number: An Easy Trick

You can quickly determine the absolute value of a number without drawing a number line. You need to follow these rules:

• Rule 1: If the number is positive, the absolute value of the number is itself.
• Rule 2: If the number is negative, drop the negative sign.

For example, the absolute value of 9 is simply 9 using rule 1.

On the other hand, the absolute value of – 16 is 16 using rule 2.

Can you determine the absolute value of 0, – 321, 1500, and -9000?

The answers are:

| 0 | = 0

| – 321 | = 321

| 1500 | = 1500

| – 9000 | = 9000

Finding the absolute value of a number is essential in adding and subtracting integers. Now that you know it, let’s proceed to our actual topic.

Operations on Integers

1. Addition of Integers

The first thing you need to consider before adding integers is to determine whether the given integers have the same or different signs. 

Integers have the same signs if both of them are positive or both of them are negative. Meanwhile, integers have different signs if one of them is positive and one of them is negative.

a. Addition of Integers with the Same Signs

To add integers with the same signs (either both are positive or both are negative):

Step 1: Add the absolute values of the given integers

Step 2: Put the common sign to the number you have obtained from Step 1.

Let’s have some examples:

Example 1: 15 + 32 = ?

Even a preschooler can answer this easy example. Of course, the answer is 47. However, let’s try answering this problem using the steps on adding integers with the same signs since 15 and 32 are both positive (same signs).

Solution:

Step 1: Add the absolute values of the given integers.

The absolute value of 15 is 15, while the absolute value of 32 is 32. We add their absolute values: 15 + 32 = 47

Step 2: Put the common sign to the number you have obtained from Step 1.

Since both 15 and 32 are positive integers, their common sign is positive. The number we obtained from Step 1 was 47. Therefore, the sign of 47 must be positive.

Indeed, 15 + 32 = 47

Example 2: What is the sum of – 210 and – 172?

Solution:

Let’s use the steps for adding integers with the same signs since – 210 and – 172 are negative integers (i.e., same signs).

Step 1: Add the absolute values of the given integers.

The absolute value of – 210 is 210, while the absolute value of – 172 is 172. We add their absolute values:

210 + 172 = 382

Step 2: Put the common sign to the number you have obtained from Step 1.

Since – 210 and – 172 are negative integers, their common sign is negative. Therefore, we put a negative sign to the number we obtained from step 1, which is 382.

Hence, the sum of – 210 and – 172 is – 382.

b. Addition of Integers with Different Signs

Now, what if the given integers have different signs? What if one integer is positive while the other is negative and vice-versa?

Just follow these steps to add integers with different signs quickly:

Step 1: Subtract the absolute values of the given numbers.

Step 2: Put the sign of the integer with a larger absolute value to the number you have obtained from Step 1.

Let’s have some examples:

Example 1: Add -19 and 25.

Solution:

-19 is a negative number, and 25 is a positive integer. They have different signs. Hence, we will use the steps above to add integers with different signs.

Step 1: Subtract the absolute values of the given numbers.

The absolute value of – 19 is 19. Meanwhile, the absolute value of 25 is 25.

Subtracting the absolute values (larger – smaller): 25 – 19 = 6

Step 2: Put the sign of the integer with a larger absolute value to the result you have obtained from Step 1.

| – 19 | =  19 and | 25 |  =  25. 

Note that the absolute value of 25 is larger than the absolute value of – 19. Also, 25 is a positive number. Therefore, the result obtained from Step 1 (6) must be a positive integer.

Hence, – 19 + 25 = 6

Example 2: Add – 32 and 15.

The given integers have different signs. Let’s use the steps for adding integers with different signs.

Solution:

Step 1: Subtract the absolute values of the given numbers.

The absolute of – 32 is 32, while the absolute value of 15 is 15.

Subtracting the absolute values (larger – smaller): 32  – 15 = 17

Step 2: Put the sign of the integer with a larger absolute value to the result you have obtained from Step 1.

| – 32 | =  32 and | 15 |  =  15. 

Note that the absolute value of – 32 is larger than the absolute value of 17. Also, – 32 is negative. Therefore, the result obtained from Step 1 (17) must be a negative integer.

Hence, – 32 + 15 = – 17

Example 3: Add – 90 and 32.

Solution:

Step 1: Subtract the absolute values of the given numbers.

The absolute of – 90 is 90, while the absolute value of 32 is 32.

Subtracting the absolute values (larger – smaller): 90  – 32 = 58

Step 2: Put the sign of the integer with a larger absolute value to the result you have obtained from Step 1.

| – 90 | =  90 and | 32 |  =  32. 

Note that the absolute value of – 90 is larger than that of 32. Also, – 90 is negative. Therefore, the result we obtained from Step 1 (58) must be a negative integer.

Hence, – 90 + 32 = – 58

Now that you have learned how to add integers, you are prepared to learn how to subtract them.

2. Subtraction of Integers

There are two steps you need to follow when subtracting integers:

Step 1: Change the operation into addition and reverse the sign of the second integer (or the subtrahend).

Step 2: Apply the rules for adding integers.

Let’s have some examples.

Example 1: What is – 19 – 5?

Solution:

Step 1: Change the operation into addition and reverse the sign of the second integer (or the subtrahend).

The first thing you have to do is to change the subtraction sign (-) into an addition sign (+). 

Afterward, reverse the sign of the second integer (or the subtrahend). The subtrahend is 5, so we reverse the sign of 5 into – 5.

– 19 + (- 5) =

Step 2: Apply the rules for adding integers.

We need to apply the rules for adding integers to finish the subtraction process.

We have obtained – 19 + (- 5)  from Step 1. This means that we need to add integers with the same signs. I hope that you still remember the rules for adding integers.

Using the rules for adding integers with the same signs:

– 19 + (- 5) = – 24

And then we’re done. The answer is – 24.

Therefore, – 19 – 5 = – 24

Example 2: Compute for: – 32 – (-12)

Solution:

Step 1: Change the operation into addition and reverse the sign of the second integer (or the subtrahend).

The first thing you have to do is to change the subtraction sign (-) into an addition sign (+). 

Afterward, reverse the sign of the second integer (or the subtrahend). The subtrahend is – 12, so we change the sign of – 12 into 12.

– 32 + 12  = 

Step 2: Apply the rules for adding integers.

We need to apply the rules for adding integers to finish the subtraction process.

We have obtained – 32 + 12  from Step 1. This means that we need to add integers with different signs.

Using the rules for adding integers with different signs:

– 32 + 12  = – 20

Therefore, – 32 + 12  = – 20

Example 3: What is -18 – (- 45)?

Solution:

Step 1: Change the operation into addition and reverse the sign of the second integer (or the subtrahend).

The first thing you have to do is to change the subtraction sign (-) into the addition sign (+). 

Afterward, reverse the sign of the second integer (or the subtrahend). The subtrahend is – 45, so we change the sign of – 45 into 45.

– 18  + 45  = 

Step 2: Apply the rules for adding integers.

We need to apply the rules for adding integers to finish the subtraction process.

We have obtained – 18 + 45  from Step 1. This means that we need to add integers with different signs

Using the rules for adding integers with different signs:

– 18 + 45  = 27

Therefore, – 18 + 45  = 27

3. Multiplication of Integers

Multiplying integers is a lot easier than adding or subtracting integers. The rules are pretty simple:

• If the integers have the same signs, multiply the integers and put a positive sign in the resulting integer.
• If the integers have different signs, multiply the integers and put a negative sign in the resulting integer.

You can use this simple reminder when multiplying integers: SAME SIGNS = POSITIVE, UNLIKE SIGNS = NEGATIVE

Let’s have some examples:

Example 1: Multiply: – 3 × – 5

Solution:

–  3 and – 5 are both negative integers. They have the same signs so their product must be positive.

Therefore, – 3 × – 5 = 15

Example 2: Multiply: 8 × – 3

Solution:

8 and – 3 have different signs, so their product must be negative.

Therefore, 8 × – 3 = – 24

4. Division of Integers

The rules for dividing integers are similar to multiplying integers:

• If the integers have the same signs, divide the integers and put a positive sign to the resulting integer.
• If the integers have unlike or different signs, divide the integers and put a negative sign to the resulting integer.

Let’s have some examples:

Example 1: Divide -18 by -2

Solution:

-18 and -2 have the same signs. So, we divide the integers, and the answer must be positive.

-18 ÷ (-2) = 9

Example 2: Divide 18 by – 2

Solution:

18 and – 2 have different signs. So, we divide the integers, and the answer must be negative.

18 ÷ (-2) = – 9

You may have wondered why the Multiplication of Integers and Division of Integers almost have the same rules. The answer is simple: Dividing integers is just multiplying an integer by the multiplicative inverse or the reciprocal (we will learn the reciprocal of a number in later topics) of the other. That’s why their rules are almost similar.

Bonus: Multiplying a Number by Zero (0)

Suppose we want to multiply an integer such as – 12 by 0. What do you think will be the result?

Simple: The answer is 0.

If you multiply any number (real, rational, irrational, integers, fraction, or decimal) by zero, the result will always be 0. This property is called the Zero Property of Multiplication.

Example 1: 1 000 000 x 0

Solution: By the Zero Property of Multiplication, the answer is 0

Example 2: π x 0

Solution: By the Zero Property of Multiplication, the answer is 0

Next topic: Order of Operations (PEMDAS)

Previous topic: Real Numbers and Imaginary Numbers

Return to the main article: The Ultimate Basic Math Reviewer

Download Printable Summary/Review Notes

Download Printable Flashcards

Test Yourself!

1. Practice Questions [Free PDF Download]

2. Answer Key [Free PDF Download]

3. Math Mock Exam + Answer Key