Numbers are everywhere!

The money in your pocket, your birthdate, class grades, and even the time you will spend reading this reviewer. All of these things involve numbers.

Although we are all familiar with numbers, not everyone knows their classifications.

In this review, let’s discuss two classes of numbers: Real and imaginary numbers.

Click below to go to the main reviewers:

Ultimate UPCAT Reviewer

Ultimate NMAT Reviewer

Ultimate Civil Service Exam Reviewer

Ultimate PMA Entrance Exam Reviewer

Ultimate PNP Entrance Exam Reviewer

Ultimate LET Reviewer

Natural or Counting Numbers

Natural numbers are used to count objects. These are the numbers you use to determine how many pets you have, how many apples you have bought from the market, or how many petals a flower has.

Natural numbers start with 1, followed by 2, then 3, and so on. Therefore, the smallest natural number is 1. Meanwhile, there’s no largest natural number.

0, negative numbers, fractions, and decimals are not natural numbers since we do not use them to count objects.

Numbers such as 14, 25, 799, 1212, 100000, and 5612312 are all examples of natural numbers.

Whole Numbers

Whole numbers are counting numbers, including 0. In other words, if you include 0 in the set of natural numbers, you will obtain the set of whole numbers.

Therefore, natural numbers are part of the set of whole numbers.

This means that all natural numbers are also whole numbers. Also, all whole numbers are natural numbers except for 0 since 0 is not a natural number.

Example: Is 510 a whole number or a natural number?

Solution: 510 is a natural number since we use it for counting. Since all natural numbers are also whole numbers, 510 is both a natural and a whole number. 

Integers

Integers are positive and negative whole numbers, including 0. Examples are 1, 0, -1, 500, -500, 2200, -3800, and so on. 

If you combine the set of all whole numbers and the set of all whole negative numbers, you now have the set of integers. Also, the set of natural numbers and the set of whole numbers are just subsets or parts of the set of integers.

Fractions and decimals are not integers. For example,  ½, -⅓, -⅔, and 0.9 are not integers. 

Rational Numbers

Any number that can be expressed as a ratio of two integers is a rational number. In simple words, a number is a rational number if there are two integers such that when the first integer is divided by the second integer, the result is the original number.

Suppose the number 18. Can you think of two integers such that when you divide the first integer by the second integer, the result is 18? 

36 and 2 are integers. Note that 36 ÷ 2 = 18. Since there are two integers such that when you divide the first integer (36) by the second integer (2) the result is 18, then 18 is a rational number.

A rational number is also a number that can be written as a fraction with integers. For example, 75 is rational since you can express it as 150⁄2, where 150 and 2 are both integers. Also, ½ is a rational number since it is a fraction composed of integers 1 and 2. 

Shown below is the formal definition of a rational number:

A rational number is any number that you can express in the form p⁄q such that p and q are both integers and q is not equal to 0.

Again, don’t worry if the definition sounds confusing because it simply means that a number is a rational number if and only if you can write it as a fraction with integers.

To make it easier for you, here is a list of numbers that can be considered rational numbers:

1. All integers are rational numbers. Example:  -1, 0, -1000, 152321, etc. are all rational numbers
2. All fractions (positive or negative) are rational numbers. Example: -5⁄3, -½, 2⁄3 , etc. are rational numbers.
3. All terminating decimals or decimals with an end (positive or negative) are rational numbers: If a decimal number has a finite or countable number of digits, that decimal number is rational. Example: 0.01, 0.99, -0.23234, -0.421, etc., are rational numbers.
4. All non-terminating (never-ending) repeating decimals (positive or negative) are rational numbers: If a decimal number has an infinite or uncountable number of digits but the digits are being repeated, then the decimal number is a rational number. Example : 0.9999… , 0.123123123123…, 0.010101…, – 0.11111…, etc. are rational numbers.

Meanwhile, non-terminating non-repeating decimals such as 0.5411346565134…, 0.28992139813…, etc are not rational numbers. Non-terminating non-repeating decimals have an uncountable number of digits that are not repeated in a certain pattern. You cannot express these non-terminating non-repeating decimals as a fraction with integers.

Note: The “three-dot” symbol that is used on some decimals is called an ellipsis. A decimal with an ellipsis means that there are digits that follow after the last digit of the number. For example, in 0.9292… the number 2 is not the last digit of the decimal number since there are digits that follow 2.

Irrational Numbers

A number that is not a rational number is an irrational number An irrational number cannot be expressed as a fraction with integers.

Examples of irrational numbers are the non-terminating non-repeating decimals such as 0.321315325453… Using this example, you cannot provide two integers such that when you divide the first integer by the second integer, the result will be 0.321315325453…

There are a lot of important irrational numbers in mathematics. For instance, the famous pi (π) which is used to calculate the circumference of a circle and the value of which is approximately 3.1416… is an irrational number. 

Real Numbers

If you combine the set of rational numbers and the set of irrational numbers, the resulting set is the set of real numbers.

Real numbers are the combination of rational and irrational numbers. -1, 0, 0.12093020…, and -½  are examples of real numbers.

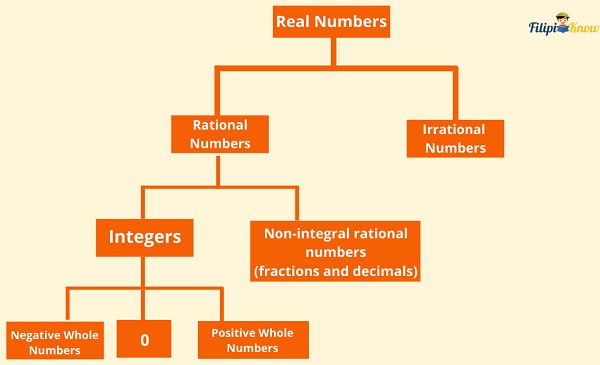
It is clearly seen that the set of the rational numbers and the set of irrational numbers are subsets of the set of real numbers.

The set of rational numbers is composed of the set of integers, fractions, and decimals. On the other hand, the set of positive whole numbers, negative whole numbers, and 0 composed the set of integers.

Therefore, the set of natural numbers, whole numbers, integers, rational, and irrational numbers are all subsets of the set of real numbers.

The Real Number Line

The real number line is a visual representation of the set of real numbers. Every point in the number line corresponds to a real number. Hence, a point in the real number line can be either a rational or an irrational number.

In the middle of the number line lies the number zero (0). On the left of zero are the negative numbers while all positive numbers are on the right of zero. 

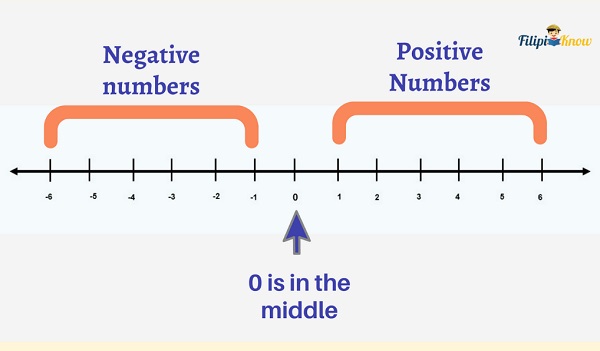
The farther you go to the left of the number line, the smaller the value of the number is. As the number line goes to the right, the larger the value of the number is.

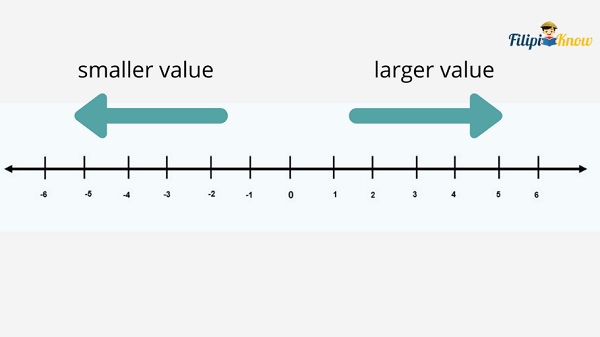
For example, – 5 is smaller in value than – 2 since – 5 can be located farther to the left compared to – 2. Meanwhile, 200 is larger in value than 100 since 200 is located farther to the right compared to 100.

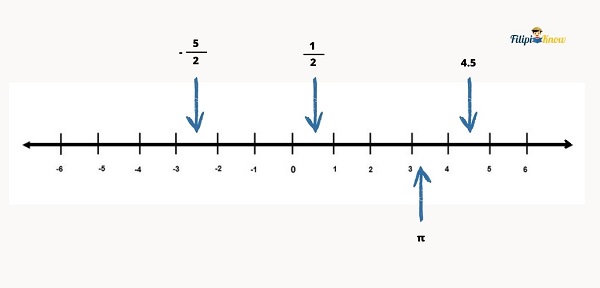
We can also plot fractions and decimals in the real number line. For instance, ½ can be located between 0 and 1, -5⁄2 can be located between -2 and -3, and 4.5 can be located between 4 and 5.

Just like rational numbers, irrational numbers can be located in the real number line. For instance, π whose value is approximately 3.1416 can be located between 3 and 4.

Imaginary Numbers

The first time I heard of imaginary numbers, it felt like hearing about unicorns. You may think that these numbers, just like unicorns, do not exist because they are called “imaginary”.

However, it is important to note that imaginary numbers also “exist” in a mathematical sense and it has practical uses in various fields.

But what exactly is an imaginary number?

An imaginary number is the square root of a negative number. Recall that the square root of a number is the number that when multiplied by itself yields the original number. For example, the square root of 16 is 4 since 4 x 4 = 16.

However, there’s no real number that gives the square root of a negative number. Suppose that I want to get the square root of -15. -15 has no square root in the set of real numbers since when a real number is multiplied by itself, the result must always be non-negative.

Mathematical mathematicians used imaginary numbers to express the square root of a negative number. They used i to represent the square root of -1. i is the basic unit of imaginary numbers or the imaginary unit.

Another interesting fact about imaginary numbers is that they cannot be located in the real number line. 

What if we combine a real number and an imaginary number? Well, what you have now is a complex number such as 3 + 5i where 3 is the real number while 5i is the imaginary number.

Next topic: Operations on Integers

Return to the main article: The Ultimate Basic Math Reviewer

Download Printable Summary/Review Notes

Download Printable Flashcards

Test Yourself!

1. Practice Questions [Free PDF Download]

2. Answer Key [Free PDF Download]

3. Math Mock Exam + Answer Key