All of us prioritize one thing over another. You most likely prioritize education over leisure, food over video games, or family over friends.

Similarly, each mathematical operation has a corresponding level of priority.

You have learned to add, subtract, multiply, and divide integers. But what if multiple mathematical operations are involved, such as in 9 + (3 x 2) – 4? What operation must be performed first, second, third, and so on? 

This review will discuss the standard way of prioritizing mathematical operations, commonly known as the order of operations or PEMDAS.

Click below to go to the main reviewers:

Ultimate UPCAT Reviewer

Ultimate NMAT Reviewer

Ultimate Civil Service Exam Reviewer

Ultimate PMA Entrance Exam Reviewer

Ultimate PNP Entrance Exam Reviewer

Ultimate LET Reviewer

   

What Is PEMDAS?

PEMDAS is an acronym for Parenthesis, Exponents, Multiplication, Division, Addition, and Subtraction. This is a standard method of determining which operations you must prioritize first, second, third, and so on. In other words, PEMDAS tells you what operation must be performed first, given a set of multiple operations.

In other math textbooks, PEMDAS is referred to as MDAS or GEMDAS.

PEMDAS implies that the operation inside the parenthesis has the highest priority or must be performed first. Then, you simplify the number with an exponent. Afterward, you multiply or divide the numbers from left to right. Finally, you add and subtract numbers from left to right. 

A fun way to remember PEMDAS is this sentence “Please Excuse My Dear Aunt Sally.” 

 

How To Solve PEMDAS Problems: 4 Steps

If there is more than one mathematical operation involved in your calculation, you must follow PEMDAS. The steps to perform PEMDAS are as follows:

1. First, perform the operation inside the parenthesis or grouping symbol.
2. Simplify any number with exponents.
3. Perform multiplication or division from left to right.
4. Perform addition or subtraction from left to right.

Note: Make sure that you can perform mathematical operations on integers because they will be applied in our succeeding examples.

Example 1: 9 + (3 x 2) – 4

The given problem has more than one operation involved. There is an addition, a multiplication, and a subtraction sign. There is also an operation inside the parenthesis. This means that we need to use PEMDAS.

Solution:

P – Perform the operation inside the parenthesis or grouping symbol.

The first thing we need to perform is the operation inside the parenthesis. In particular, we are going to solve 3 x 2 first.

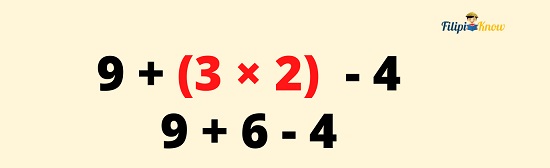
The operation inside the parenthesis is 3 x 2 which is equal to 6.

E – Simplify any number with exponents.

There are no exponents involved in the given problem. Thus, we will skip this step.

MD – Perform multiplication or division from left to right.

No more multiplication or division is involved in 9 + 6 – 4. Therefore, we will skip this step.

AS – Perform addition or subtraction from left to right.

We perform addition first since it is the first one that appears from the left. 9 + 6 = 15. Lastly, we perform subtraction: 15 – 4 = 11

Let’s review what we have done:

9 + (3 x 2) – 4

9 + 6 – 4

15 – 4

11

Hence, using PEMDAS,  9 + (3 x 2) – 4 = 11

I hope you still remember the rules of operations on integers because we will use them for the following example.

Example 2: (-17 – 2) x 3 – 9

Let us use PEMDAS to answer the above problem.

P – Perform the operation inside the parenthesis.

The operation inside the parenthesis is – 17 – 2. By subtracting the given integers, we will obtain – 17 – 2 = – 19.

E – Simplify any number with exponents.

The given problem doesn’t have any exponent. Thus, we will skip this step.

MD –  Perform multiplication or division from left to right.

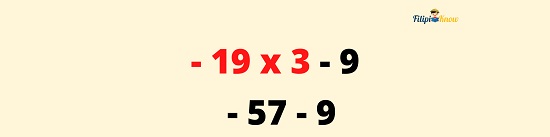
AS –  Perform addition or subtraction from left to right.

Here’s a quick review of what we have done:

         (-17 – 2) x 3 – 9

            (-19) x 3 – 9

-57 – 9

– 66

Hence, using PEMDAS,  (- 17 – 2) x 3 – 9 = -66

Before our third example, let’s discuss how to compute numbers with exponents.

 

What is an Exponent?

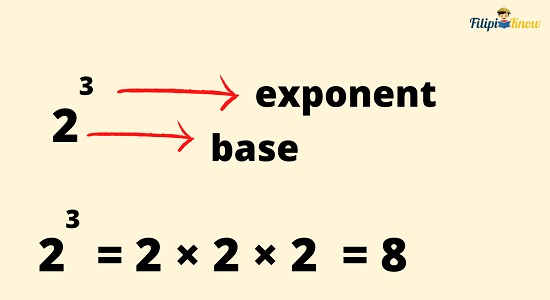
An exponent is a number written on the upper right of another number called the base. This means that the base is raised to a specific power. 

For example, in 2³, the exponent is 3 (the small letter above or the superscript), while the base is 2.

How To Compute Numbers with an Exponent

Although an exponent is written as a tiny number above the base, its impact is powerful!

The exponent corresponds to the number of times the base must be multiplied by itself. For example, in 2³, we have two as the base while three as the exponent. This means you must use the base (i.e., 2) three times in a multiplication process.

2³ = 2 x 2 x 2 = 8

Therefore, 2³ = 8.

Now, can you compute for 9²?

Our exponent is 2, which means we need to use 9 two times in a multiplication process:

9² = 9 x 9 = 81

Therefore, 9² = 81

Remember how to compute exponents since we will use this method for our third example.

Example 3: What is the value of 3³ – (9 x 2) ÷ 6?

Let us apply PEMDAS to solve the question.

P – Perform the operation inside the parenthesis or grouping symbol.

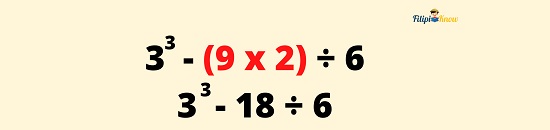
E – Simplify any number with exponents.

3³ is a number with an exponent. Hence, we need to simplify it. Note that 3³ = 3 x 3 x 3 = 27

MD – Perform multiplication or division from left to right.

Only division is involved, and no more multiplication sign is left. Hence, we solve 18 ÷ 6

AS – Perform addition or subtraction from left to right.

Here is a quick review of what we have done:

 3³ – (9 x 2) ÷ 6 

3³ – 18 ÷ 6

27 – 18 ÷ 6

27 – 3

24

Hence, using PEMDAS, 3³ – (9 x 2) ÷ 6 = 24

Example 4:  Compute for 81 ÷ (4² –  7)  x 3

We can determine the answer to the given problem above using PEMDAS.

As usual, we start our computation with the operation inside the parenthesis. However, two things are involved inside the parenthesis: An exponent and a subtraction sign. Note that it is easier to perform the exponent first before performing subtraction.

81 ÷ (4² –  7)  x 3

81  ÷ (16 – 7) x 3

Now, we can perform subtraction which is inside the parenthesis:

81  ÷ (16 – 7) x 3

     81  ÷ 9 x 3

We have already performed P of PEMDAS. Since no more exponents are involved, we move to the next operations, multiplication, and division (MD).  Let’s go back to the same problem:

  81  ÷ 9 x 3

Since division appeared first from the left, we will perform it first.

  81  ÷ 9 x 3

       9 x 3

Lastly, we will perform multiplication

   9 x 3 = 27

Let’s try to answer something more challenging in our fifth example.

Example 5: Compute for  200 – 15² + (144 ÷ (-12) ) x (14 ÷ (-2))

Let us begin by performing the operations inside the parenthesis. There are two parentheses. Thus, we will perform the operations inside them simultaneously.

We already did the P of PEMDAS, so we are now on E, which is exponents. We simplify the number with an exponent.

We are now on the MD part of PEMDAS. There is only multiplication involved, and there is no division sign left. Hence,

Next is the AS part of PEMDAS. Since subtraction appeared first from the left, it must be performed first.

Finally, let us add the remaining numbers

Here is a quick review of what we have done above:

200 – 15² + (144 ÷ (-12) ) x (14 ÷ (-2) )

200 – 15² + (- 12) x (- 7)

200 – 225 + 84

-25 + 84

59

Hence, using PEMDAS,  200 – 15² + (144 ÷ (-12) ) x (14 ÷ (-2) ) = 59

 

Next topic: Factors and Multiples

Previous topic: Operations on Integers

Return to the main article: The Ultimate Basic Math Reviewer

 

Download Printable Summary/Review Notes

Download Printable Flashcards

Test Yourself!

1. Practice Questions [Free PDF Download]

2. Answer Key [Free PDF Download]

3. Math Mock Exam + Answer Key