Laws of Exponents Worksheet (With Answers)

Exponents’ discovery revolutionized how we compute enormous and small values. Exponents help us understand the concepts of compound interest, population growth, bacterial growth, and radioactive decay. They also serve as a tool to express distances between astronomical bodies, describe computer memory, and express some scientific scales.
With this reviewer containing the laws of exponents worksheet, you’ll learn about exponents and the rules applied to perform mathematical operations with them.
Click below to go to the main reviewers:
Ultimate PMA Entrance Exam Reviewer
Ultimate PNP Entrance Exam Reviewer
Table of Contents
Review on Exponents
What Is an Exponent?
An exponent is a small number written on the upper right of another number (or variable) called the base. It tells you that the base is raised to the power of the exponent.
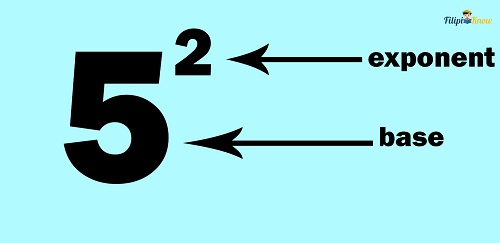
For example, in 52, the exponent is the small number (i.e., 2), written above and on the right of 5. Meanwhile, the larger number (i.e., 5) is the base. The exponent tells us that the base, which is 5, is raised to the power of 2.
Computing Whole Numbers With Exponents
The exponent indicates how many times the base will be multiplied by itself. Thus, in 52, the exponent of 2 tells you that five is multiplied by itself twice.

Hence, 52 = 25.
Example 1: Compute 35
Solution: The exponent of 5 tells us that three is multiplied by itself five times.
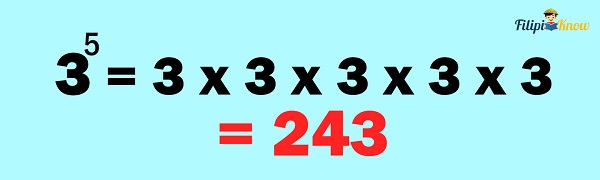
Therefore, 35 = 243
To generalize, given am where a and m are both real numbers, it means that a is multiplied by itself m times.
So far, we have tried to calculate numbers with exponents. However, all of our examples have positive bases. In our next section, let us discuss how to compute exponents of negative bases.
Computing Negative Numbers With Exponents
Let’s say we want to compute -22. This means that only the number 2 is being raised to the power of 2 and not -2. We can also interpret -22 as – 1 x 22
Note that by applying the order of operations (PEMDAS), you must perform exponents before multiplication.
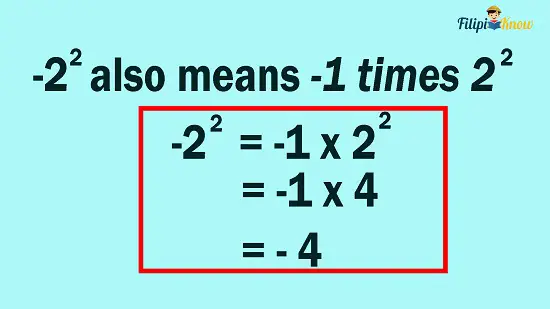
Hence, to compute -22, you must first start computing for 22.
22 = 4
Afterward, multiply four by – 1:
-22 = – 4
On the other hand, if we put a negative number inside a parenthesis, we are raising the number with the negative sign to the exponent.
For example, suppose we want to compute for (- 2)2. This means that – 2 is being raised to two.
Thus, to compute (- 2)2, we multiply – 2 by itself two times:
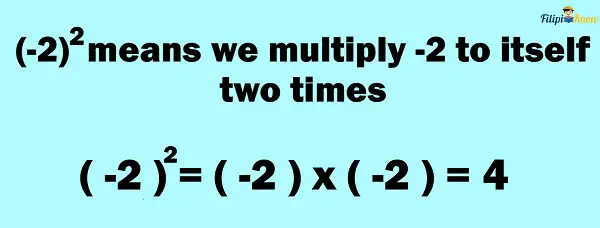
Thus, (- 2)2 = 4.
From the computations we have performed above, we can conclude that -22 ≠ (- 2)2
Thus, a question that requires computing a negative number raised to an exponent may come in two forms. Here’s how to solve each of them:
- Case 1: To compute –ab where a and b represent specific real numbers, we evaluate ab first and then multiply the result by – 1.
- Case 2: To compute (- a)b where a and b represent specific real numbers, we multiply –a by itself b times.
Example 1: What is the value of -94?
Solution: -94 is an example of Case 1. To compute for -94, we need to calculate 94 first. Afterward, multiply the result by -1:
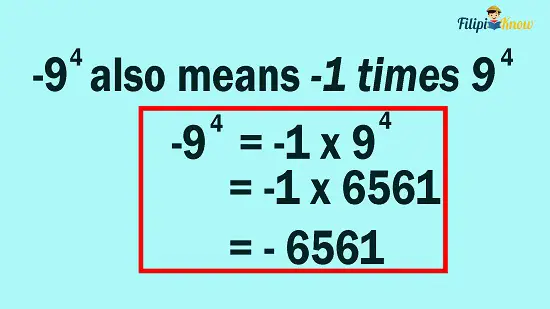
Example 2: What is the value of (- 9)4?
Solution: Since – 9 is inside the parentheses, it indicates that – 9 is what is being raised to the power of 4. Thus, we need to multiply – 9 by itself four times.
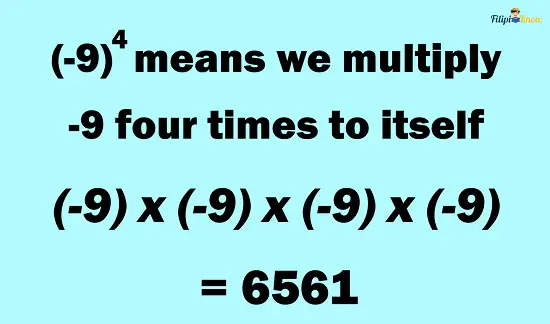
Variables Raised to an Exponent
When a variable has an exponent, the variable is raised to a specific power. The variable’s exponent tells you how many times it is being multiplied by itself.
For instance, what does m3 mean?
The exponent in m3 tells us that the variable m is raised to the power of 3. In other words, it tells us that m is multiplied thrice.
m3 = m ⋅ m ∙ m
Note: As shown above, the solid dot is an alternative way to express multiplication.
Example 1: Write k5 in expanded form.
Solution: The exponent in k5 tells us that the variable k is multiplied by itself five times. Thus, the expanded form of k5 is:
k5 = k ∙ k ∙ k ∙ k ∙ k
Example 2: Express u ∙ u ∙ u ∙ u ∙ u ∙ u in exponential form.
Solution: Note that the variable u is used six times. Hence, we must use an exponent of 6. Thus:
u ∙ u ∙ u ∙ u ∙ u ∙ u = u6
Variables With Coefficients
Take a look at this algebraic expression: 5m3
Recall that 5 is the numerical coefficient of m3 since it is a number multiplied by a variable.
Now, what does the exponent of 3 tell us in 5m3? What is the base of that exponent?
If you look closely at 5m3, the variable m is the only one raised to the power of 3, and 5 is not included. Hence, the base of the exponent 3 in 5m3 is m only and not 5m.
Thus 5m3 means 5(m ∙ m ∙ m)
Now take a look at this algebraic expression: (5m)3
What does the exponent of 3 tell us in (5m)3? What is the base of that exponent?
This time, the base is 5m. It means that 5m is being multiplied by itself thrice.
Thus, (5m)3 means 5m ∙ 5m ∙ 5m
In summary: When expanding a coefficient and variable raised to an exponent, check first the base of the exponent. Determine whether the coefficient is included in the base of the exponent or not.
- 5m3 = 5(m ∙ m ∙ m). In this case, the numerical coefficient is not included in the base of the exponent.
- (5m)3 = 5m ∙ 5m ∙ 5m. In this case, the numerical coefficient is included in the base of the exponent.
Example 1: Write -3x5 in expanded form.
Solution: The variable x is the only one raised to the power of 5. Thus, only the variable x is the base of exponent 5 in the given, and -3 is not included.
Thus, -3x5 = -3(x ∙ x ∙ x ∙ x ∙ x)
Example 2: Write (-3x)5 in expanded form.
Solution: The existence of the parentheses indicates that both the -3 and x in -3x are raised to the power of 5. Thus, -3x is the base of exponent 5.
In other words, (-3x)5 = -3x ∙ –3x ∙ -3x ∙ –3x ∙ -3x
Laws of Exponents
There are a lot of computations involving exponents that you will encounter as you study algebra. However, laws or specific rules must be observed to perform these computations correctly. These laws are referred to as the Laws of Exponents.
Let us discuss these laws in this section one by one.
1. Product Rule
Suppose we want to multiply x2 by x4. Note that x2 and x4 have the same base. How can we multiply them?
One possible method is to expand x2 and x4:
x2 = x ∙ x
x4 = x ∙ x ∙ x ∙ x
Multiplying the expanded values:
x2 ∙ x4
(x ∙ x) ∙ ( x ∙ x ∙ x ∙ x)
Note that we can express the product of the expanded values in exponential form:
(x ∙ x) ∙ ( x ∙ x ∙ x ∙ x) = x ∙ x ∙ x ∙ x ∙ x ∙ x = x6
Therefore, x2 ∙ x4 = x6
What have you noticed? Have you noticed a relationship between the exponents in x2 ∙ x4 = x6?
Yes, the exponent in x6 is just the sum of the exponents of x2 and x4.
You now know what the first law of exponent is all about. That is,
Product Rule: When multiplying exponential expressions with the same base, copy the common base and add the exponents.

Thus, when multiplying expressions with the same base, you do not have to expand the given expressions to determine the answer. Just apply the product rule.
Remember that you cannot apply the product rule if the given bases are different. For example, if you multiply a2 by p3, you cannot apply the product rule since the given bases are different.
Example 1: Compute for 24 ∙ 22
Solution: We have expressions with the same bases (i.e., 2) multiplied together. Thus, we can apply the product rule.
Let us copy the common base first:
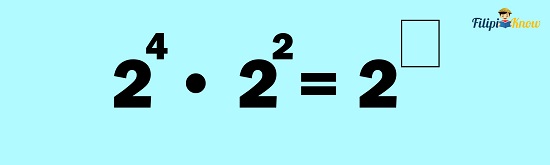
Then, add the exponents:

Thus, using the product rule: 24 ∙ 22 = 26
Example 2: Multiply b5 by b3
Solution: Since we have the same bases being multiplied together, we can apply the product rule:
Let us copy the common base first:
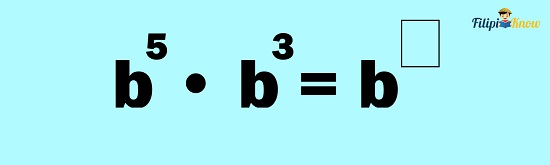
Then, add the exponents:
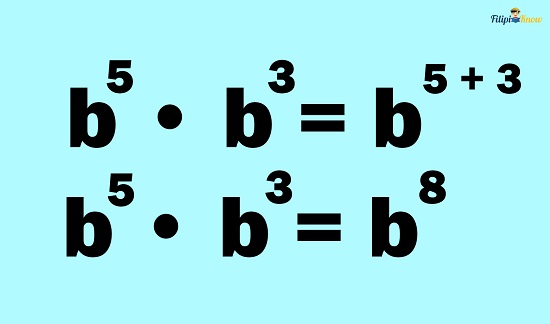
Therefore, using the product rule: b5 ∙ b3 = b8
Example 3: Multiply a3b2 by a2b4
Solution: We have two bases involved here, the variables a and b.
Thus, we need to apply the product rule, each for a and b:
Let us copy the common bases first:
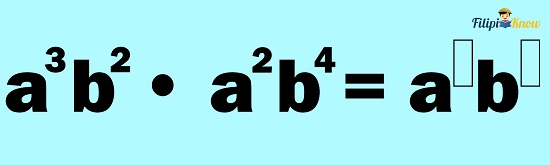
Add the exponents for the common bases.
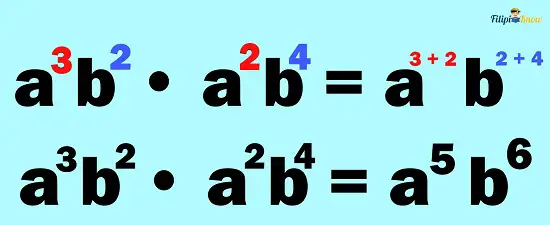
Hence, a3b2 ∙ a2b4 = a5b6
Example 4: Multiply (x + 5)6 by (x + 5)3
Solution: In this case, the common base is x + 5. Hence, we can apply the product rule.
Let us copy the common base first:
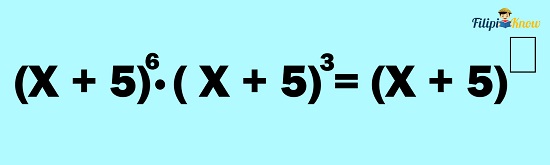
Add the exponents:
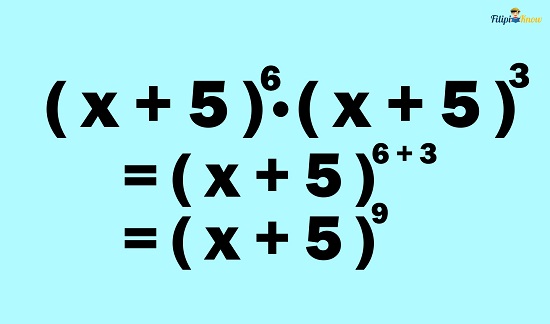
Therefore, (x + 5)6 ∙ (x + 5)3 = (x + 5)9
Example 5: Compute for a(a2)
Solution: If two variables are written together with the other one enclosed in parentheses, it implies that the variables are being multiplied. Since we have a common base in the given (i.e., a), we can apply the product rule here.
Note that if a number or a variable has no exponent written above it, it implies that the exponent is 1.
Let us copy the common base first:
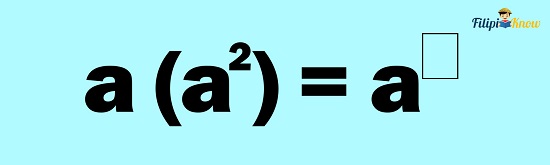
Add the exponents:
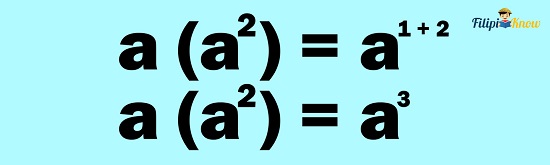
Therefore, a(a2) = a3
2. Quotient Rule
The Quotient Rule is the opposite of the Product Rule.
It states that if you divide exponential expressions with the same base, you can just copy the common base and then subtract the exponents.

Example 1: Compute for x7 ÷ x3
Solution: We can apply the quotient rule since we are dividing exponential expressions with the same base.
Let us copy the common base first:
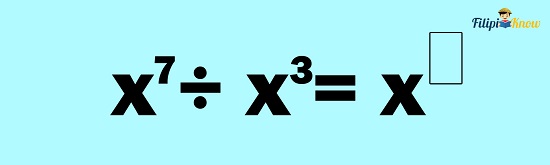
Subtract the exponents:

Therefore, x7 ÷ x3 = x4
Example 2: Simplify x9⁄x4
Solution: x9⁄x4 also means x9 ÷ x4. Since we are dividing exponential expressions with the same base, we can apply the quotient rule.
Let us start by copying the common base:

Finally, subtract the exponents:
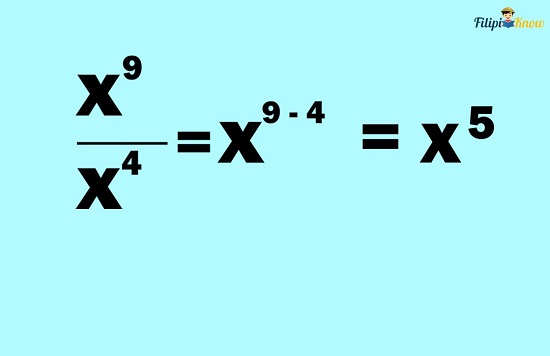
Therefore, x9⁄x4= x5
Example 3: Simplify p8q2⁄p6q
Solution: We have two bases involved: the variables p and q. Thus, we will use the quotient rule for the variables p and q.
Copying the common bases:
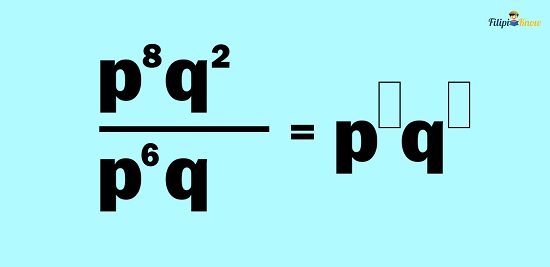
Finally, subtract the exponents for each of the common bases.

Hence, p8q2⁄p6q = p2q
Example 4: Divide 1,000,000,000 by 1,000,000.
Solution: Note that we can express 1,000,000,000 as 109. On the other hand, we can express 1,000,000 as 106. Therefore, we can answer the problem by dividing 109 by 106.
Since we have a common base (i.e., 10), we can apply the quotient rule:
Let us copy the common base first:
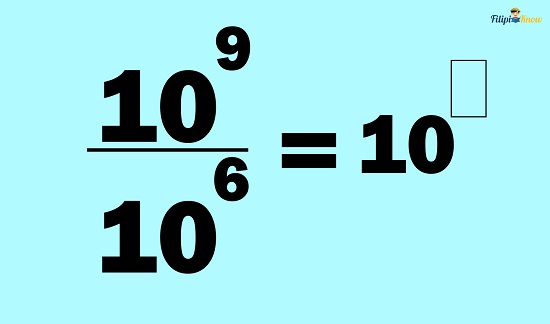
Then, subtract the exponents:
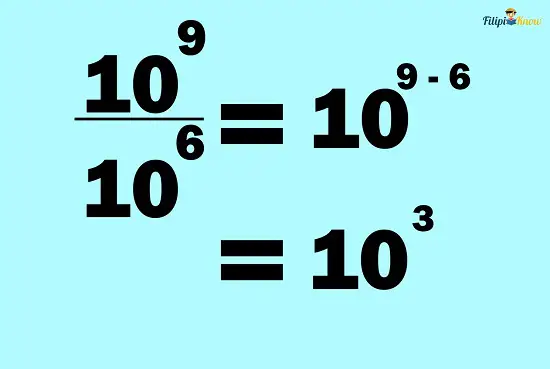
Therefore, the answer is 103 or 1000.
Tip: We can express a multiple of 10 into exponential form quickly by counting the number of zeros it has. For example, 1,000,000,000 has nine zeros. Thus, if we express 1,000,000,000 in exponential form, we can determine the exponent to be used based on the number of zeros it has. Therefore 1,000,000,000 = 109
3. Power Rule
Imagine a number raised to an exponent and then raised to another exponent. What do you think will happen?
Suppose we have b2 and want to raise it, say to the power of 3. This will give us (b2)3
Can we express (b2)3 using a single exponent only? The power rule states that we can!
The power rule states that if a number is raised to an exponent and then all is raised to another exponent, you can combine the exponents into one by multiplying them.

Example 1: Simplify (k4)2
Solution: Notice that the entire k4 is raised to 2. We can combine the exponents into one by multiplying them by applying the power rule. Thus,
(k4)2 = k4 × 2 = k8
Therefore, (k4)2 = k8
Example 2: What is the value of (32)3?
Solution: Applying the product rule:
(32)3 = 32 ×3 = 36
Now, all we need to do next is expand 36:
3 ∙ 3 ∙ 3 ∙ 3 ∙ 3 ∙ 3 = 729
Therefore, (32)3 = 729
Example 3: Simplify (a5)2
Solution: Applying the product rule:
(a5)2 = a5 × 2 = a10
Therefore, (a5)2 = a10
Example 4: Simplify (8y5)2
Solution: Note that the base of the exponent 2 is 8y5. This means that we need to apply the power rule both for 8 and y5:
(8y5)2 = 82y5 × 2 = 82y10
Since 82 = 8 ∙ 8 = 64, then 82y10 = 64y10
Therefore, (8y5)2 = 64y10
4. Power of a Product Rule
If an expression has more than one variable multiplied together and raised to a specific power, we can simplify that expression using the power of the product rule. This rule allows us to raise the variables involved in the multiplication process to the given exponent.
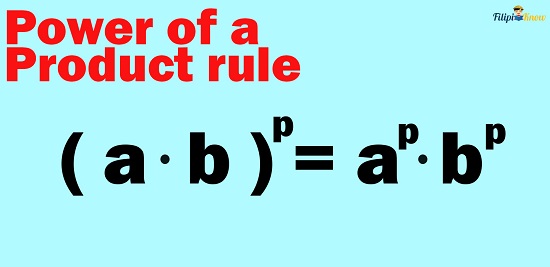
Example 1: Simplify (xy)2
Solution: The given expression has two variables multiplied (xy) and raised to the power of 2. This means we can simplify it using the power of a product rule.
The power of the product rule allows us to “distribute” the exponent to each variable:
(x y)2 = (x2)(y2)
Therefore, (xy)2 = x2 y2
Example 2: Simplify (a4b3)3
Solution: Let us apply the power of the product rule to simplify the given expression.
We start by “distributing” 3 to each of the variables:
(a4b3)3 = (a4)3 (b3)3
To further simplify the expression, we can apply the product rule to each variable:
(a4)3 (b3)3 = a4 × 3 b3 × 3 = a12b9
Hence, (a4b3)3 = a12b9
Example 3: Simplify (4a3b2)2
Solution: Let us apply the power of the product rule to simplify the given expression. Note that we should also raise 4 to the power of 2:
(4a3b2)2 = (4)2 (a3)2 (b2)2
Now, we apply the product rule to each variable:
(4)2(a6)(b4)
Lastly, since 42 = 16:
16a6b4
Therefore, (4a3b2)2 = 16a6b4
5. Power of a Quotient Rule
The power of the quotient rule is the opposite of the previous rule. It tells us that if variables are divided and raised to a specific power, we can simplify the expression using the power of the quotient rule.

Suppose we have the expression m⁄n, and we want to raise it to the power of 3: (m⁄n)3
Since we have two variables (m and n) divided together and raised to a specific power, we can apply the power of the quotient rule.
This rule allows us to raise the variables involved in the division process to the given exponent.
(m⁄n)3 = (m3⁄n3)
Example 1: Apply the power of the quotient rule to (x⁄y)2
Solution: Through the power of the quotient rule, we can distribute the exponent to the variables involved in the division process:
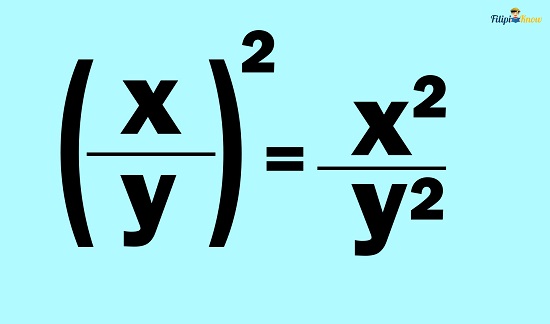
Therefore, using the power of the quotient rule, (x⁄y)2 = x2⁄y2
Example 2: Simplify (a4⁄b2)2
Solution: Since we have two variables (a4 and b2) divided together and raised to a specific power, we can apply the power of the quotient rule:
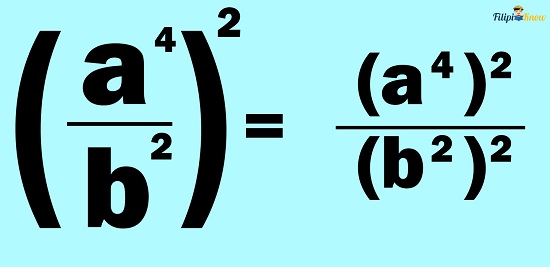
Notice that we can simplify the expression further using the product rule:
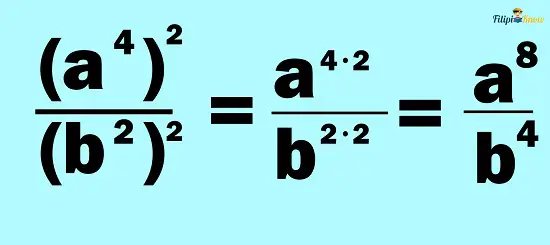
Therefore, (a4⁄b2)2 = a8⁄b4
6. Zero-Exponent Rule
What happens if you raise a number or a variable to the power of zero?
The zero-exponent rule tells us that the result will be 1.
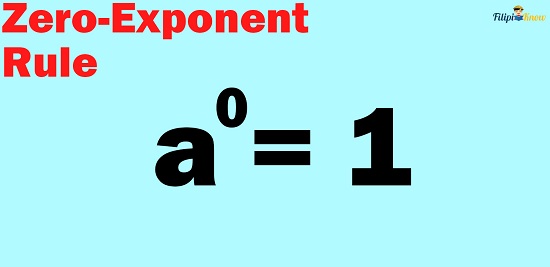
The Zero-Exponent Rule states that any nonzero base raised to 0 equals 1.
Example 1: Suppose that m ≠ 0; what is the value of m0?
Solution: By the zero-exponent rule, m0 = 1.
Example 2: What is the value of 1090?
Solution: By the zero-exponent rule, 1090 = 1
Example 3: Simplify 15x0
Solution: We know that by the zero-exponent rule, x0 = 1. Take note that x0 is multiplied by 15 in 15x0. Since x0 = 1:
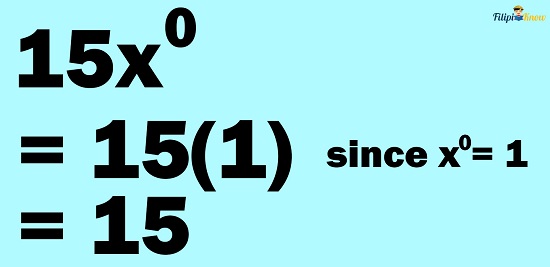
Hence, 15x0 = 15
Example 4: Simplify a0b2c
Solution: By the zero-exponent rule, a0 = 1. Since a0 is multiplied to b2c in the given expression a0b2c:
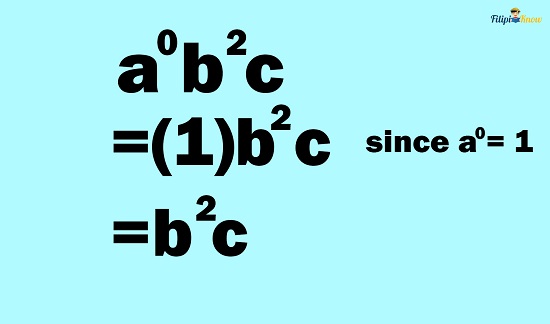
Hence, a0b2c = b2c
7. Negative Exponent Rule
The negative exponent rule states that if a base is raised to a negative number, the base should be put to the denominator, and the given negative exponent changed into a positive exponent.

Let’s apply the negative exponent rule to 2-2. Using the rule, we can put the base (i.e., 2) to the denominator. Note that the denominator of 2-2 is 1. Once we put the base into the denominator, we can change the negative exponent into a positive exponent.

Therefore, 2-2 = ¼
Let us look at the examples below to understand this rule further.
Example 1: What is the value of 5-3?
Solution: Using the negative exponent rule, we can express 5-3 as 1⁄5
Example 2: Express y-1 as an expression without a negative exponent.
Solution: Using the negative exponent rule, we can express y-1 as 1⁄y with no negative exponent involved.
Thus, the answer is 1⁄y.
Example 3: Express a2b-3c without a negative exponent.
Solution: We can apply the negative exponent rule to express a2b-3c without a negative exponent. However, since b– 3 is the only base raised to a negative exponent, we can only apply the negative exponent rule to b– 3, and it is the only base that we will put in the denominator.
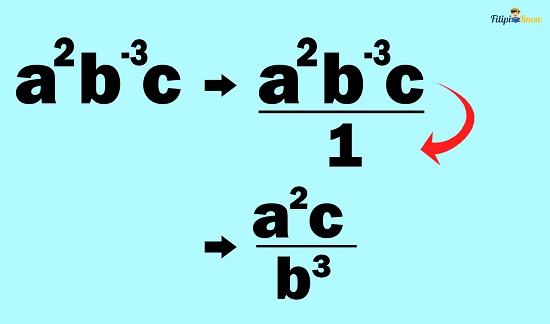
Therefore, a2b-3c can be written without a negative exponent as a2c⁄b3
Laws of Exponents Summary
We are now done discussing the mathematical rules that govern the exponential expressions. As a recap, here’s a table that summarizes the laws of exponents.
| Product Rule | am ∙ an = am + n |
| Quotient Rule | am⁄an= am – n |
| Power Rule | (am)n = amn |
| Power of a Product Rule | (a b)p = ap bp |
| Power of a Quotient Rule | (a⁄b)m = am⁄bm, where b ≠ 0 |
| Zero Exponent Rule | a0 = 1 |
| Negative Exponent Rule | a-m = 1⁄am |
Simplifying Exponential Expressions Using the Laws of Exponents
An exponential expression is simplified if there are fewer terms and exponents involved. Furthermore, a simplified exponential expression has positive exponents.
As we simplify various exponential expressions, we have to apply different laws of exponents discussed above.
Example 1: Simplify 5p0q-2
Solution: We can simplify the given expression by making all its exponents positive.
Let us start by applying the zero-exponent rule:
5p0q-2
5(1)q-2 (since p0 = 1)
5q-2
We can then remove the negative exponent using the negative exponent rule:
5q-2
5⁄q2
Thus, the answer is 5⁄q2
Example 2: Simplify (a4⁄a2)2
Solution 1: Note that we can distribute the exponent (i.e., 2), which is outside the parentheses, to the bases that are inside the parentheses using the power of the quotient rule:
(a4⁄a2)2 = a4 × 2⁄a2 × 2 = a8⁄a4
Since we are dividing the same bases, we can apply the quotient rule:
a8⁄a4 = a8 – 4 = a4
Therefore, (a4⁄a2)2 = a4
You can also simplify the given expression using the alternative solution below.
Solution 2: This time, let us start applying the quotient rule since we are dividing the same bases:
(a4⁄a2)2 = (a4 – 2)2 = (a2)2
Notice that we can now apply the power rule since (a2)2 is an expression raised to an exponent and then raised to another exponent.
(a2)2 = a2 × 2 = a4
Example 3: Simplify [(x + y)2(x + y)3]-1
Solution: We can start by making the negative exponent positive. To do this, put the base into the denominator (negative exponent rule). The base in the given expression is the entire (x + y)2(x + y)3
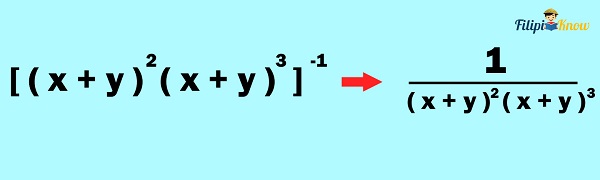
We can simplify the expression further using the product rule since we are multiplying the same bases:
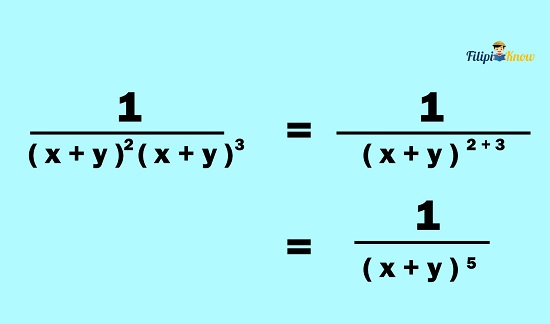
Therefore, the answer is 1⁄(x + y)5
Next topic: Logarithms
Previous topic: Algebraic Expressions
Return to the main article: The Ultimate Basic Math Reviewer
Download Printable Summary/Review Notes
Download Printable Flashcards
Test Yourself!
1. Practice Questions [Free PDF Download]
2. Answer Key [Free PDF Download]
3. Math Mock Exam + Answer Key
Written by Jewel Kyle Fabula
in College Entrance Exam, LET, NAPOLCOM Exam, NMAT, PMA Entrance Exam, Reviewers, UPCAT
Jewel Kyle Fabula
Jewel Kyle Fabula graduated Cum Laude with a degree of Bachelor of Science in Economics from the University of the Philippines Diliman. He is also a nominee for the 2023 Gerardo Sicat Award for Best Undergraduate Thesis in Economics. He is currently a freelance content writer with writing experience related to technology, artificial intelligence, ergonomic products, and education. Kyle loves cats, mathematics, playing video games, and listening to music.
Copyright Notice
All materials contained on this site are protected by the Republic of the Philippines copyright law and may not be reproduced, distributed, transmitted, displayed, published, or broadcast without the prior written permission of filipiknow.net or in the case of third party materials, the owner of that content. You may not alter or remove any trademark, copyright, or other notice from copies of the content. Be warned that we have already reported and helped terminate several websites and YouTube channels for blatantly stealing our content. If you wish to use filipiknow.net content for commercial purposes, such as for content syndication, etc., please contact us at legal(at)filipiknow(dot)net
