Imagine yourself as a mathematician during the 16th century. This is an era without calculators, computers, and spreadsheets, so dealing with calculations of numbers with multiple digits is tedious and time-consuming. 

Things changed when a Scottish mathematician named John Napier developed a revolutionary idea to ease the way calculations are made. He is one of the mathematicians who developed logarithms, a convenient tool that minimizes time spent on complex calculations. 

In this review, you’ll learn logarithm evaluation without using a calculator so you can confidently perform complex computations in any exam.

Click below to go to the main reviewers:

Ultimate UPCAT Reviewer

Ultimate PMA Entrance Exam Reviewer

Ultimate LET Reviewer

Logarithms

Logarithms are an alternative way of expressing quantities that involve exponents.

For instance, the mathematical sentence 3² = 9 can be written in its equivalent logarithmic form, log₃9 = 2. 

Recall that the exponent tells us the number of ways the base is used as a factor in a multiplication sentence. For instance, 3² = 9 means we must use 3 as a factor twice in a multiplication sentence to get 9 (i.e., 3 x 3 = 9 ). 

Meanwhile, logarithms tell us how many times a number must be multiplied to obtain another number. For instance, log39 = 2 (read as “log of 9 to the base 3 is equal to 2”) tells us that if we use an exponent to transform 3 into 9, we must use 2. 

You will understand further how logarithms work once we discuss their components in the next section. 

Components of a Logarithm

A logarithm has the following major components:

1. The “log” function, which states that we are dealing with a logarithm
2. The base or the small number below the “log” symbol 
3. The argument or the larger number on the right of the base. 
4. Finally, the number on the right of the equal sign is the exponent.

For instance, in log₃9 = 2, the base is 3, the argument is 9, and the exponent is 2.

The logarithm shows us what exponent must be used so that the base will be equal to the argument. In the case of log₃9 = 2, it tells us that 2 must be used as the exponent so that 3 becomes 9.

Here is the general notation for the logarithms:

log_am = n 

Where a, m, and n are real numbers with a ≠ 1 and m ≠ 0. a is called the base, m is the argument, and n is the exponent.

Note: The “formal” way to read log_bx = y is “logarithm of x to the base b is equal to y.” 

Evaluating Logarithms

In this section, we will discuss how to evaluate a logarithm.

Logarithm evaluation means identifying an exponent that must be used for the base so that we can obtain the argument.

Let us compute for log₄16. This means we must consider the exponent used for 4 to get a value of 16. 

Note that if we multiply 4 by itself, we can get 16 (i.e., 4 x 4 = 16); hence, we must use an exponent of 2 for 4 to get 16.

Therefore, log₄16 = 2.

Sample Problem: Compute the value of the following:

1. log₃27
2. log₂32
3. log₅25
4. log₇1

Solution:

1. Note that if we multiply 3 by itself three times, we can get 27 (i.e., 3 x 3 x 3 = 27). Therefore, log₃27 = 3.
2. If we multiply 2 by itself five times, we can get 32 ( 2 x 2 x 2 x 2 x 2 = 32). Therefore, log₂32 = 5.
3. Multiplying 5 by itself two times will result in 25. Therefore, log₅25 = 2.
4. To evaluate the value of log₇1, we think of a power to which we must raise 7 to obtain 1. The zero-exponent rule shows that any real number raised to zero equals 1. Hence, we must raise 7 to the power of 0 to get 1. Therefore, log₇1 = 0.

Evaluating Logarithms With an Argument of 1

Recall that logarithms generally are expressed as log_am = n where a, m, n are real numbers with a ≠ 1 and m ≠ 0. But what if the argument (or m) is equal to 1? How can we evaluate the value of the logarithm?

Say we want to evaluate the value of log₆1. 

log₆1 tells us what exponent we should raise 6 to get 1.

Recall that the zero-exponent rule states that any real number raised to 0 will result in 1. So, if we raise 6 to the power of 0, we can obtain 1. Mathematically, 6⁰ = 1.

Therefore, the value of log₆1 must be equal to 0 (log₆1 = 0). 

To sum up, if the argument of the logarithm is 1, then the value of the logarithm is automatically 0 as per the zero-exponent rule:

log_a1 = 0, where a is a real number

Transforming Exponential Form Into Logarithmic Form and Vice Versa

1. Exponential Form Into Logarithmic Form

To convert a quantity in exponential form into logarithmic form, follow the steps below:

1. Write the “log” sign to indicate that you’re using the logarithm operator
2. Write the base of the exponential form as the base of the logarithmic form (i.e., the small number on the right of the log)
3. Write the value of the exponential form as the argument of the logarithmic form (i.e., the number on the right of the base of the logarithmic form)
4. Write the exponential form as the exponent of the logarithmic form.

Generally, a quantity in exponential form b^y = x is written as log_bx = y in logarithmic form. 

Sample Problem: Write 5³ = 125 in logarithmic form.

Solution: Using the steps on transforming the exponential form into the logarithmic form:

Step 1: Write the “log” sign to indicate that you’re using the logarithm operator

Note: the boxes in the expression above serve as placeholders for the remaining components of the logarithm. 

Step 2: Write the base of the exponential form as the base of the logarithmic form (i.e., the small number on the right of the log)

The base of 5³ = 125 is 5. Hence we use it as the base of the logarithmic form:

Step 3: Write the value of the exponential form as the argument of the logarithmic form (i.e., the number on the right of the base of the logarithmic form) 

The value of the exponential form 5³ = 125 is 125. Hence, we will use it as the argument of the logarithmic form.

Step 4: Write the exponential form as the exponent of the logarithmic form

Finally, we use “3” (the exponent in 5³ = 125) in the logarithmic form.

log₅125 = 3

2. Logarithmic Form Into Exponential Form

To transform a quantity expressed in logarithmic form into exponential form, we have to follow these steps:

1. Drop the “log” sign
2. Use the base of the logarithmic form (i.e., the small number on the right of the “log” symbol) as the base of the exponential form
3. Use the exponent of the logarithmic form (i.e., the number on the right of the equal sign) as the exponent for the exponential form
4. Use the argument as the value of the exponential form

Sample Problem: Express log₅125 = 3 into exponential form.

Solution:

Step 1: Drop the “log” sign

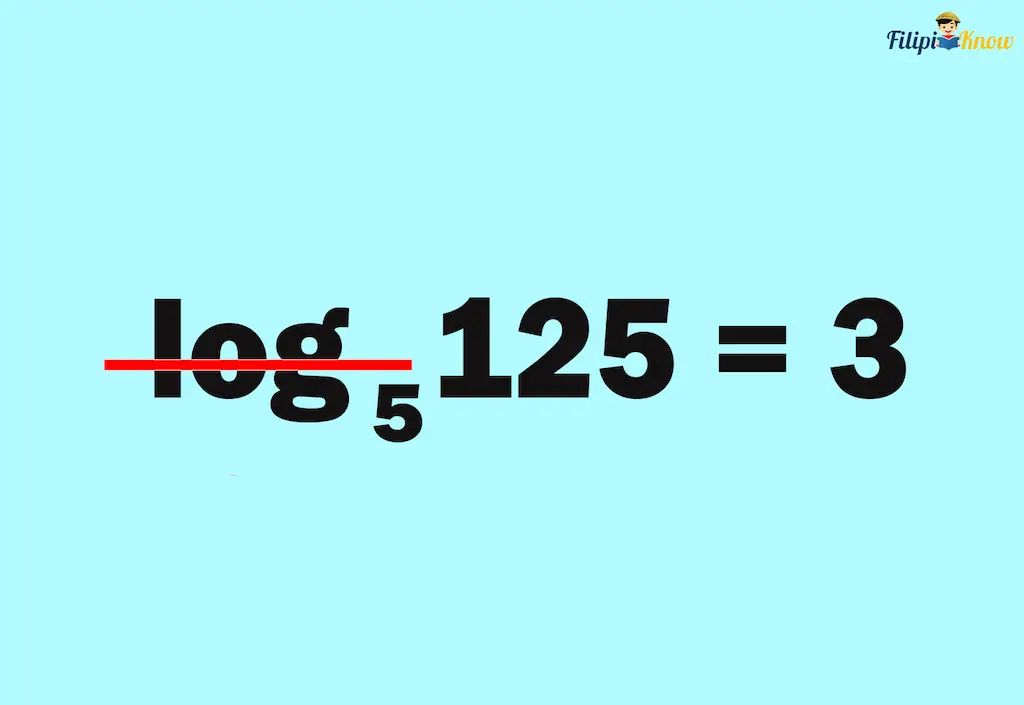
Step 2: Use the base of the logarithmic form (i.e., the small number on the right of the “log” symbol) as the base of the exponential form

The base of the logarithmic form is 5, so we use it as the base of the exponential form:

Step 3: Use the exponent of the logarithmic form (i.e., the number on the right of the equal sign) as the exponent for the exponential form

The exponent of the logarithmic form is 3, so we’ll use it as the exponent in the exponential form.

Step 4: Use the argument as the value of the exponential form

Finally, we use 125 (the argument in log₅125 = 3) as the value of the exponential form. 

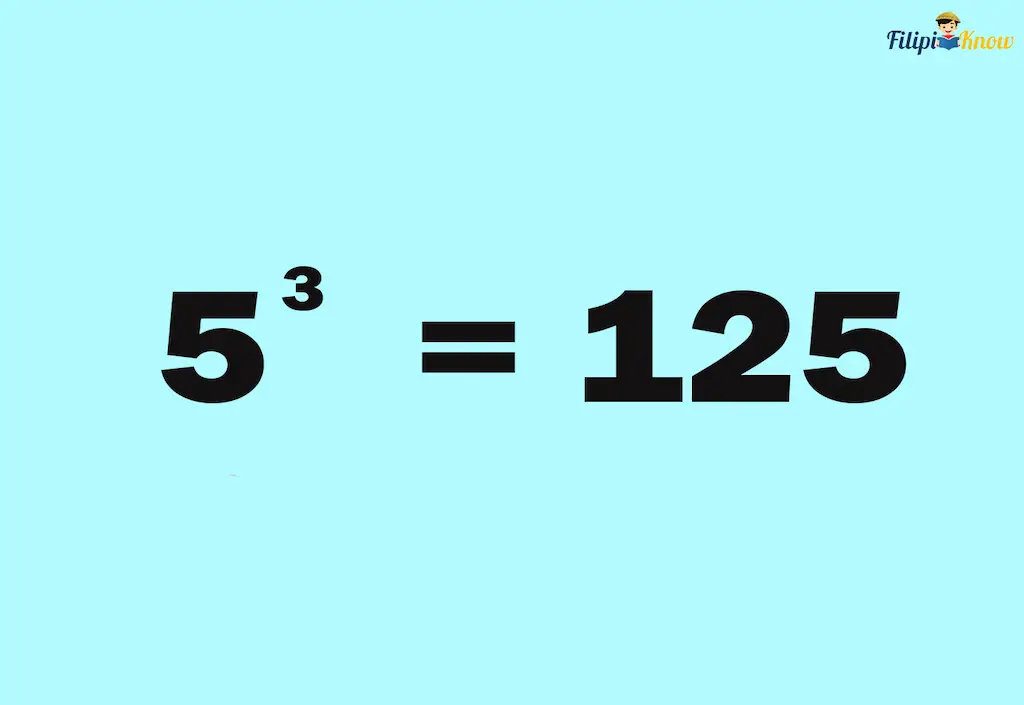
Therefore,log₅125 = 3 can be written as  5³ = 125.

Common and Natural Logarithms

1. Common Logarithms

Common logarithms are logarithms with a base of 10. 

For instance, log₁₀100 = 2 can be considered a common logarithm.

In a common logarithm, we no longer need to write the “10” as the base. We leave it blank since it is already understood that we are dealing with a common logarithm.

For instance, log 100 = 2 automatically means log₁₀100 = 2.

Suppose we want to write a common logarithm to its equivalent exponential form. In that case, all we need to do is use ten as the base, use the logarithm argument as the value of the exponential form, and then use the exponent of the logarithm form as the exponent of the exponential form. For instance, log 100 = 2 is equivalent to 10² = 100.

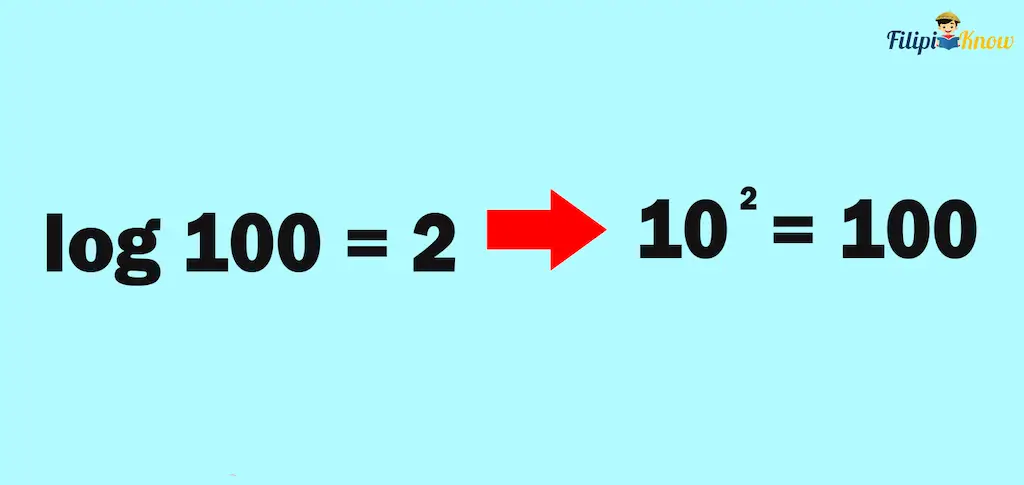
Note that it’s not always easy to compute the common logarithm of numbers. For instance, log 350 (log10350) cannot be determined easily through manual computation since its value is not a whole number (log10350 = 2.544). In these cases, scientific calculators are the most convenient tool to use. Since we are reviewing for exams that prohibit using any calculator, we will limit our discussion to common logarithms that can be evaluated only through manual calculation. 

Sample Problem: Evaluate log 1000

Solution: log 1000 is a common logarithm. Although it appears to have no base, it means the base is 10. Therefore, log 1000 = log₁₀1000.

To find the value of log₁₀1000, we need to think of how many times ten must be multiplied by itself to get 1000. Note that if we multiply ten by itself thrice, the result will be 1000 (10 x 10 x 10 = 1000). Thus, log₁₀1000 = 3. 

2. Natural Logarithms

Natural logarithms use a “special number” as the base. This number is an irrational number represented as e. Formally, e is called Euler’s number (named after the mathematician Leonhard Euler). e is approximately equal to 2.718… 

log_e10 is an example of a natural logarithm since it uses the base e. 

However, we do not write natural logarithms like your ordinary logarithms. We use the symbol “ln” instead of “log” and omit the base e. So, log_e10 can be written as ln 10 (read as “natural logarithm of 10”). Another example: log_e1 is equal to ln 1.

Let’s write a natural logarithm to its equivalent exponential form. We use the constant e as the base of the exponential form, the argument as the value of the exponent, and the logarithm value as the exponent of the exponential form. For instance, if we transform ln x = y to exponential form, we’ll have e^y = x. 

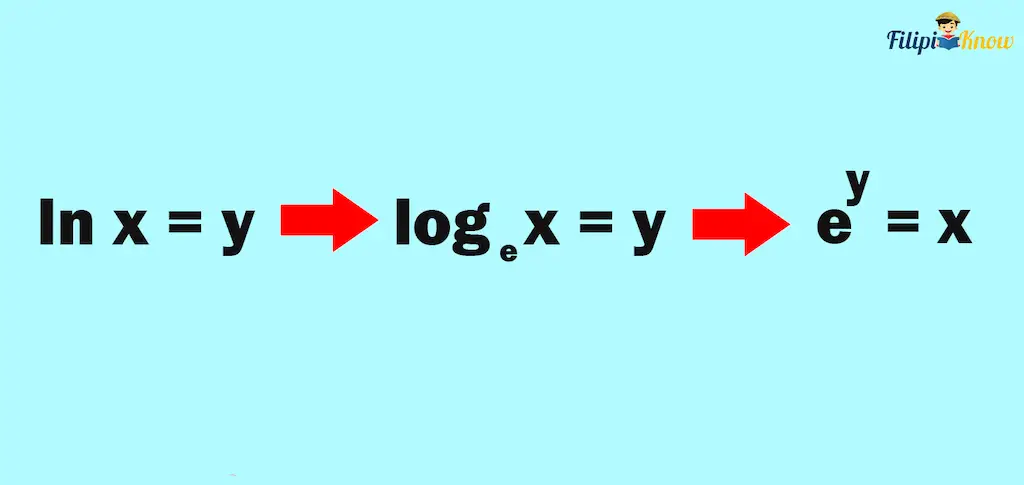
Natural logarithms are widely applied in different real-life calculations, such as for exponential growth and decay of microorganisms, compound interest, statistical analysis, calculus, physical sciences, and more. 

Properties of Logarithms

Now that you know logarithms, let us discuss their mathematical properties. These properties allow us to calculate operations involving logarithms. 

Note that the properties below also apply to common logarithms and natural logarithms.

Property of Logarithms	In symbols
Product Property of Logarithms	logaPQ = logaP + logaQ
Quotient Property of Logarithms	loga(P∕Q) = logaP – logaQ
Power Property of Logarithms	logaPq = q logaP

1. Product Property of Logarithms

This property states that the logarithm of products can be expressed as the sum of the logarithms:

log_aPQ = log_aP + log_aQ

For instance, let us express log₂8 as a sum of logarithms. We can do this by simply thinking of some factors of 8.

4 and 2 are factors of 8 since 4 x 2 = 8. Therefore, we can express log₂8 as log₂(4 x 2).

According to the product property, we can express log₂8 = log₂(4 x 2) as the sum of the logarithms of the factors of 8: log₂8 = log₂(4 x 2) = log₂4 + log₂2.

Therefore, log₂8 = log₂4 + log₂2.

Sample Problem 1: Express log₂5 + log₂4 as a single logarithm.

Solution: By applying the product property of logarithms, we just multiply the arguments of the given logarithms. 

log₂5 + log₂4 = log₂(5 x 4) = log₂20

Sample Problem 2: Given that log 3 ≈ 0.48 and log 2 ≈ 0.30. What is the approximate value of log 6?

Solution: Since log 3 and log 2 are common logarithms, they have the same base of 10. This means that we can apply the product property to them. 

Note that “log 3 ≈ 0.48” means that the approximate value of log 3 is 0.48. This means that log 3 is not exactly 0.48 since this value is just an approximation. The “ ≈ “ symbol denotes an approximation of a particular quantity.

Applying the product property, we have: log 6 = log (3 x 2) = log 3 + log 2 

This means that the value of log 6 is equal to the value of log 3 + log 2:

log 6 = log 3 + log 2

Using the given approximate values of log 3 and log 2:

log 6 = log 3 + log 2

log 6 ≈ 0.48 + 0.30

log 6 ≈ 0.78

Hence, the approximate value of log 6 is 0.78 (the value of log 6, when computed using a calculator, is 0.77815… which is extremely near to our obtained value). 

Sample Problem 3: Expand log₄(7a(b + 4)) using the product property of logarithms.

Solution: Note that in log₄(7a(b + 4)), the argument 7a(b + 4) is the product of 7a and b + 4. Furthermore, 7a is also the product of two quantities: 7 and a.

Therefore, log₄(7a(b + 4)) = log₄(7 ∙ a ∙ (b + 4)). By product rule, we can now express this as the sum of logarithms:

log₄(7a(b + 4)) = log₄(7 ∙ a ∙ (b + 4)) = log₄7 + log₄a + log₄(b + 4)

2. Quotient Property of Logarithms

This property states that the logarithm of the quotient can be expressed as the difference of logarithms.

For instance, let us express log₂6 as the difference between logarithms. We think of two numbers such that when these numbers are divided, the result will equal 6. For instance, 12 ÷ 2 = 6. Hence, log₂6 can be expressed as log₂(12∕2).

By the quotient property of logarithms, we can express log₂6 as the difference between the logarithm of the numbers that, when divided, results in 6: log₂(12∕2) = log₂12 – log₂2. 

Sample Problem 1:

Solution: The argument is

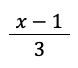
which is the quotient of x – 1 and 3. By the quotient property of logarithms, we can express the logarithm of the quotient of x – 1 and 3 as the difference between the logarithm of x – 1 and the logarithm of 3. 

By applying the quotient property of logarithms:

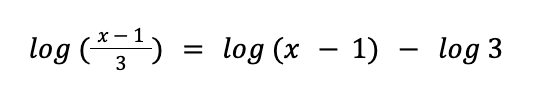
Sample Problem 2:

Solution: The argument is the quotient of 9 and b. By the quotient property of logarithms, we can express the logarithm of a quotient of 9 and b as the difference between the logarithm of 9 and b.

By applying the quotient property of logarithms:

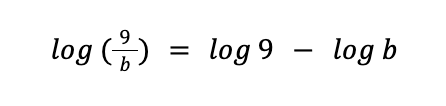
3. Power Property of Logarithms

The power rule of logarithms states that the logarithm of a quantity raised to an exponent is equal to the exponent times the logarithm of the quantity. 

log_aP^q = q ∙ log_aP

For instance, log₂x² is a logarithm with a quantity raised to an exponent (x²). By the power property of logarithms, we can express it as follows: 2 ∙ log₂x

The power property of logarithms allows you to “move” the exponent to the left of the logarithm symbol. 

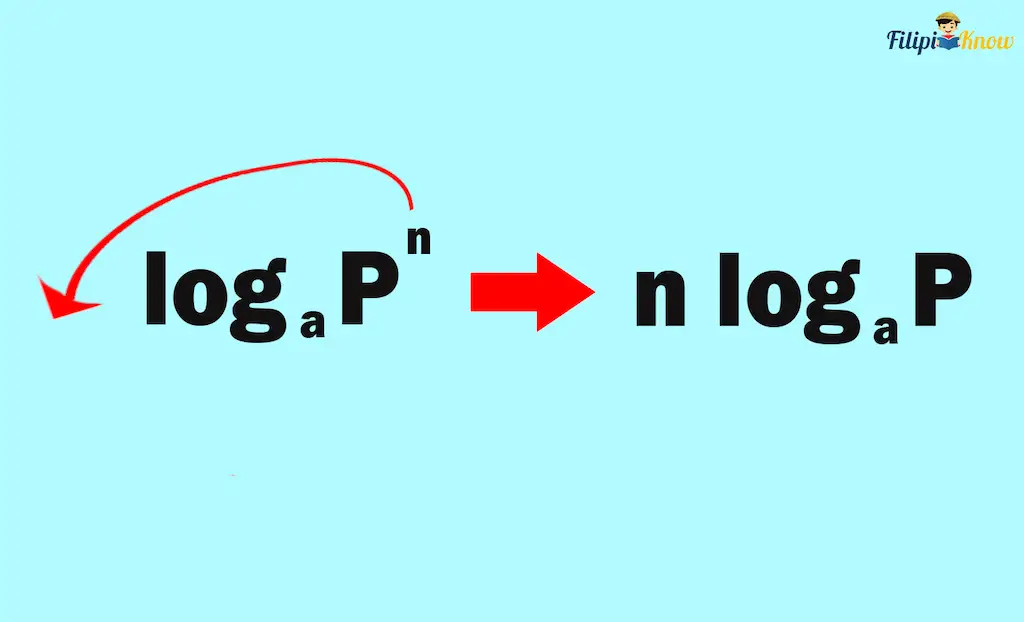
Sample Problem 1: Expand log a³ 

Solution: Since we are dealing with a logarithm that has an argument with a quantity raised to an exponent (a³), we can apply the power property of logarithms.

log a³ = 3 ∙ log a = 3 log a

Hence, the answer is 3 log a.

Sample Problem 2: Expand ln j²

Solution: By applying the product property of logarithms:

ln j² = 2 ∙ ln j = 2 ln j

Therefore, the answer is 2 ln j.

More Sample Problems on Properties of Logarithms

Sample Problem 1: Expand log₄a²b

Solution: The argument in the expression log₄a²b is a²b which is the product of a² and b. Hence, we can apply the product property of logarithms to start expanding the given expression:

log₄a²b = log₄a² + log₄b

Note that we can still expand the expression log₄a² since we have an argument with a quantity raised to an exponent (a²). We can apply the power property of logarithms for this case:

log₄a²b = log₄a² + log₄b

                                log₄a²b = 2 log₄a + log₄b

Hence, the expanded form of log₄a²b is 2 log₄a + log₄b.

Here’s the summary of what we have performed above:

log₄a²b

log₄a² + log₄b Product Property of Logarithms

2 log₄a + log₄b Power Property of Logarithms

Sample Problem 2: Expand ln x²y³

Solution: The argument in the expression ln x²y³ is x²y³ or x² and y³. This means we can apply the product property of logarithms to expand the given expression.

ln x²y³ = ln x² + ln y³

Note that we can still expand both ln x² and ln y³ since they involve arguments that are quantities raised to an exponent (x² and y³). Thus, we can apply the power property of logarithms for this case:

ln x²y³ = ln x² + ln y³

ln x²y³ = 2 ln x + 3 ln y

Hence, the answer for this example is 2 ln x + 3 ln y.

Here’s the summary of our calculation above:

ln x²y³

ln x² + ln y³ Product Property of Logarithms

2 ln x + 3 ln y Power Property of Logarithms

Sample Problem 3:

Solution:

The argument of the given logarithm is the quotient of 3a² and 2(a + b). Hence, we can apply the quotient property to expand the given logarithm.

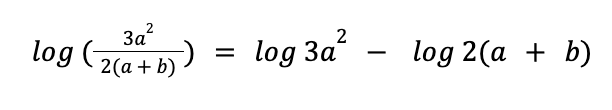
Notice that we can expand both log 3a² and log 2(a + b). Let us expand log 3a² first.

The argument of log 3a² is 3a^2, which is the product between 3 and a². As per product property:

log 3a² = log 3 + log a²

We can still expand log a² by applying the power property:

log 3a² = log 3 + 2 log a

Therefore, we now have the following:

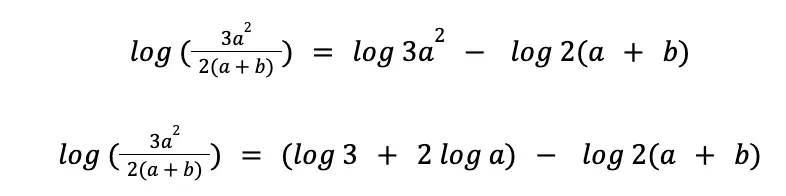
Now, let us focus on log 2(a + b). The argument here is 2(a + b), the product of 2 and a + b. Hence, we can apply the product property:

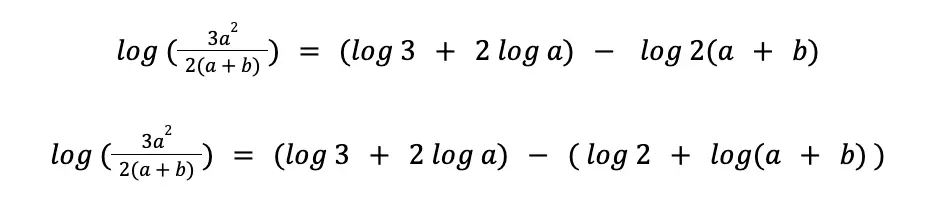
Thus, the final answer is (log 3 + 2 log a) – ( log 2 + log(a + b))

Here’s the summary of what we have performed above:

Simplifying Logarithms

Simplifying logarithmic expressions means expressing them as a single logarithm. We can do this by applying the properties of logarithms we’ve learned from the previous section. 

For instance, suppose we want to express log₃10 + log₃5 as a single logarithm. 

The expression log₃10 + log₃5 involves the mathematical operation of addition. Note that we have learned in the previous section that the logarithm of a product can be expressed as the sum of logarithms (product property). Hence, we can apply the reverse of this property and express the sum of logarithms as the logarithms of a product. 

By product property, we can express log₃10 + log₃5 as the logarithm of the product of 10 and 5 (to the base 3):

log₃10 + log₃5 

 log₃(10 x 5) = log₃50 Product Property of Logarithms

Hence, the simplified form of log₃10 + log₃5 is log₃50.

Sample Problem 1: Simplify log₂8 + log₂7 

Solution: By the product property, we can express the sum of logarithms as the logarithm of their product:

log₂8 + log₂7 

log₂(8 x 7) Product Property of Logarithms

log₂56

Thus, the answer is log₂56.

Sample Problem 2: Simplify log₃(x + 5) + log₃x + log₃4

Solution: By the product property of logarithms, we can express the sum of logarithms as the logarithm of their product:

log₃(x + 5) + log₃x + log₃4

log₃[(x + 5) ∙ x ∙ 4]

log₃(4(x)(x + 5))

log₃(4x(x + 5))

log₃(4x² + 20x)

Thus, the simplified form is log₃(4x² + 20x).

Sample Problem 3: Apply the properties of logarithms to simplify ln 6 + ln 3 – ln 2

Solution: We are now dealing with two operations in the given logarithmic expression: addition and subtraction. 

Let us deal with the addition sign first. By product property, we can express the sum of logarithms as the logarithm of their product:

ln 6 + ln 3 – ln 2

ln (6 x 3) – ln 2

ln 18 – ln 2

The resulting logarithmic expression ln 18 – ln 2 can be simplified further. The difference between logarithms can be expressed as the logarithm of their quotient using the quotient property. Thus:

ln 18 – ln 2 = ln (18∕2) = ln 9

Thus, the final answer is ln 9.

Here’s a summary of our solution above:

ln 6 + ln 3 – ln 2

ln (6 x 3) – ln 2 Product Property of Logarithms

ln 18 – ln 2

ln (18/2) Quotient Property of Logarithms

ln 9

Sample Problem 4: Simplify 3 log₂a + log₂b

Solution: Note that by power rule, we can express the product of a constant and the logarithm of a quantity as the logarithm of the quantity raised to the constant. Note that 3 log₂a is the product of a constant (i.e., 3) and a logarithm of a quantity (log₂a). Hence, we can apply the power rule to simplify it:

3 log₂a + log₂b

log₂a³ + log₂b Power Rule of Logarithms

Now, we can apply the product rule to complete the solution:

log₂a³ + log₂b

log₂a³b Product Rule of Logarithms

Thus, the final answer is log₂a³b.

Next topic: Polynomials

Previous topic: Laws of Exponents

Return to the main article: The Ultimate Basic Math Reviewer

Download Printable Summary/Review Notes

Download Printable Flashcards

Test Yourself!

1. Practice Questions [Free PDF Download]

2. Answer Key [Free PDF Download]

3. Math Mock Exam + Answer Key