Algebraic expressions come in different forms. However, certain expressions in algebra are significant and offer a lot of practical applications. These expressions are called polynomials.

In this review, we’ll discuss what polynomials are, the types of polynomials, and how to solve polynomials involving different mathematical operations.

Click below to go to the main reviewers:

Ultimate UPCAT Reviewer

Ultimate NMAT Reviewer

Ultimate PMA Entrance Exam Reviewer

Ultimate PNP Entrance Exam Reviewer

Ultimate LET Reviewer

   

What Are Polynomials?

A polynomial is an algebraic expression where the exponents of its variables are whole numbers.

As you may recall, whole numbers are positive counting numbers, including 0. Thus, the exponents in the variables of a polynomial are all positive counting numbers or 0. If a variable has an exponent of 0, the variable is a constant.

3x⁴ + 2x³ – x²y + 3 is an example of a polynomial since all the variables’ exponents are whole numbers.

 

What Expressions Are NOT Polynomials?

Now that you know what polynomials are, it is essential to understand what makes an expression non-polynomial. Here’s a list of algebraic expressions that are not considered polynomials:

1. Expressions with fractional or decimal exponents in the variable are not polynomials

For example, 4x^1/2 + 2y³ is not a polynomial since one of its variables, which is x, has a fractional exponent of ½.

2. Expressions with negative exponents in the variable are not polynomials

For example, 2a^-3b – 5a²b³ + ab is not a polynomial since one of its variables, a, has a negative exponent of – 3. 

3. Expressions with variables in the denominator are not polynomials

For example, 3x – 2⁄y is not a polynomial since it has a variable (y) in the denominator. 

How about x + y⁄2? Is this polynomial?

Although 2 is the denominator, 2 is not a variable. This means that x + y⁄2 can be considered a polynomial since it has no variable in the denominator.

Why does a variable in the denominator disqualify an algebraic expression as a polynomial?

As per the negative exponent rule, if a variable is raised to a negative exponent, we should put that variable in the denominator so that the variable will now have a positive exponent.

If a variable is in the denominator, it implies that before the negative exponent rule was applied, the variable had a negative exponent in the numerator.

We know that a negative exponent in the variable makes an expression a non-polynomial.  This is the reason why variables in the denominator make an expression non-polynomial.

4. Expressions with variables under the radical sign are not polynomials

Square root (√) and cube root (∛) are some examples of radical signs.

As an example, let’s consider the expression √x – y. Since it has a variable (x) under the radical sign, √x – y is not a polynomial.

How about √2 + x? Is this polynomial?

Look at the radical sign. Note that 2 is inside the radical sign. 2 is a constant, not a variable. Thus, we can consider √2 + x as a polynomial.

 

Terms of a Polynomial

A term in a polynomial consists of a number multiplied by a variable with a whole number exponent. The constant part is also a term of the polynomial.

The name polynomial comes from “poly” (Greek) which means many, and “nomen” (Latin) which means name (in this case, “term”). This means that a polynomial consists of different terms.

The terms in a polynomial are separated by addition or subtraction signs. 

Take, for example, the polynomial 9×2 + 36xy + 4y2 + 3.  The terms in this polynomial are 9×2, 36xy, 4y2, and 3. Notice that addition signs separate these terms.

Example: Determine the terms in 3x² + 5y – 2xz

Solution: The terms in the given polynomials are 3x², 5y, and 2xz.

Like Terms

Two or more terms are like terms if their variables and exponents (of the variables) are the same. The numerical coefficient of like terms can be different.

For example, 5y² and 3y² are like terms because these terms have the same variable (y), and their exponents are the same (which is 2).

On the other hand, 7x² and 5a² are not like terms because these terms have different variables.

Also, 5x² and 5x³ are not like terms because even if the variables of these terms are the same, the exponents are different.

Example 1: Are 2xz and 5xz like terms?

Solution: Yes, because these terms have the same variables (which are x and z).

Example 2: Which of the following does not belong to the group of like terms: 5a²b, -4a²b, 3a²b², and 9a²b?

Solution: 3a²b² does not belong to the group because it has a different exponent for its variable b. 

 

Degree of a Polynomial

The degree of a polynomial is the highest exponent of the variable of a polynomial.

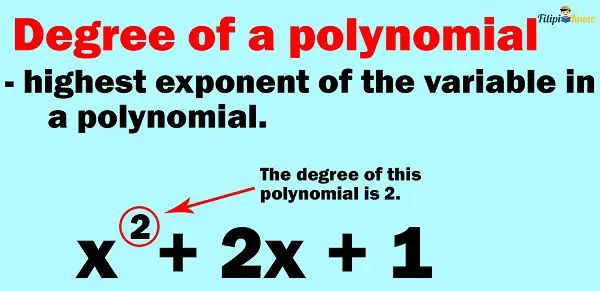
Example: What is the degree of the polynomial 3k⁷ – 5k² + k – 9?

Solution: The highest exponent of the variable in the polynomial is 7. Thus, the degree of the polynomial is 7.

If a polynomial has more than one variable, we add the exponents on each term, and the highest resulting sum is the degree of the polynomial.

 

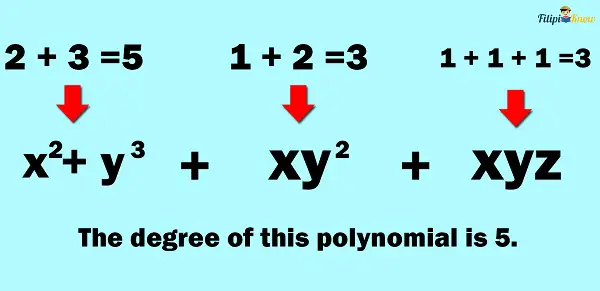
Types of Polynomials

We can classify polynomials according to degree or their number of terms.

1. Types of Polynomials According to the Number of Terms

Types of Polynomials According to Number of Terms	Number of Terms
Monomial	A polynomial with one term
Binomial	A polynomial with two terms
Trinomial	A polynomial with three terms
Multinomial	A polynomial with four terms and above

If we base the polynomial classification on the number of terms, the polynomial could be a monomial, binomial, trinomial, or multinomial.

• Monomial – an expression that has one term. This means that a constant, a variable, or a product of a constant and a variable with an exponent is a monomial. Examples are 4, a, 5x, -9y², and 4a²b.
• Binomial – an expression that has two terms. Examples are x + 2, 2y + z, 4ab – 3b², and p²q – 3.
• Trinomial – an expression that has three terms. Examples are x² + 2xy + y² , 3x – y + 5, and 6x³y + y – 9.
• Multinomial – an expression with more than three terms. Examples are a + 2ab + 3abc + 4bcd and 4x²yz + xy³z – xyz² + xyz + 1.

2. Types of Polynomials According to Degree

Types of Polynomials According to Degree	Degree
Constant	0
Linear	1
Quadratic	2
Cubic	3
Quartic	4
Quintic	5

If we base the classification of a polynomial on its degree, the polynomial could be a constant, linear, quadratic, cubic, quartic, or quintic. 

• Constant –  a polynomial with a degree of 0. For example, the classification of 9 according to its degree is constant since its highest exponent is 0. Note that we can express 9 as 9x⁰.
• Linear – a polynomial with a degree of 1. For example, x + y is linear since the highest exponent of its variables is 1. Also, 3x + 9 is linear since the highest exponent of the variable is 1.
• Quadratic – a polynomial with a degree of 2. For example, x² + 2x + 1 is quadratic since the highest exponent of its variable is 2.
• Cubic – a polynomial with a degree of 3. For example, x³ + 3x² + 3x + 1 is cubic since the highest exponent of its variable is 3.
• Quartic – a polynomial with a degree of 4. For example, x⁴ + 4x² + 8x + 2 is quartic since the highest exponent of its variable is 4.
• Quintic – a polynomial with a degree of 5. For example, x⁵ + 5x³ + 8x² + 2x – 3 is quantic since the highest exponent of its variable is 5.

 

Standard Form of a Polynomial

A polynomial is written in its standard form if the terms of the polynomial are arranged in a manner where the exponents of the variable are in decreasing order.

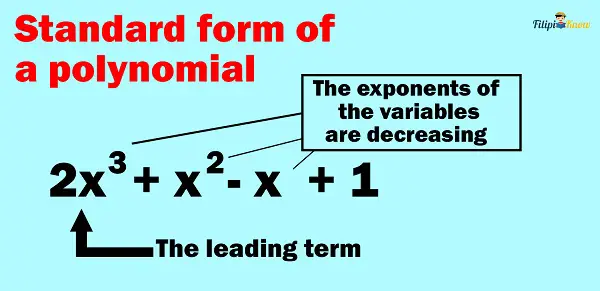
If we express a polynomial in its standard form, the first term of that polynomial is called the leading term. Thus, the leading term is the term of the polynomial with the highest exponent.

Example 1: Write 8y² + y³ – 4y + y⁵ in standard form.

Solution: We write the terms of the polynomial so that the exponents of the variables are in decreasing order. Thus, the standard form of the given polynomial is  y⁵ + y³ + 8y² – 4y.

Example 2: What is the leading term of 5z⁸ + 2z + z⁷ – 2?

Solution: To determine the leading term of this polynomial, we should write it first in standard form. If we express the polynomial in standard form, we have 5z⁸ + z⁷ + 2z – 2. The first term of this polynomial in standard form is 5z⁸. Therefore, 5z⁸ is the leading term.

 

Operations on Polynomials

This section will discuss how to solve polynomials involving the four fundamental operations.

1. Addition of Polynomials

To learn how to add polynomials, follow the steps below:

1. Arrange the given polynomials in standard form
2. Place the like terms of the given polynomials in columns 
3. Add the like terms

Example 1: Add 5x² + 3x + 2 and 2x² + x – 1

Solution:

Step 1: Arrange the given polynomials in standard form. Note that the given polynomials are already written in standard form since the exponents of their variables are in decreasing order. Hence, we can skip this step.

Step 2: Place like terms of the given polynomials in columns. Recall that the terms of given polynomials are like terms if the variables and the exponents of these variables are the same. Recall also that the numerical coefficients of like terms can be different.

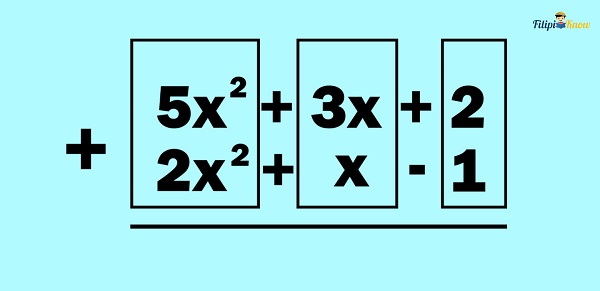
Step 3: Add the like terms. To add like terms, we add the numerical coefficients and bring down the common variable and exponent.

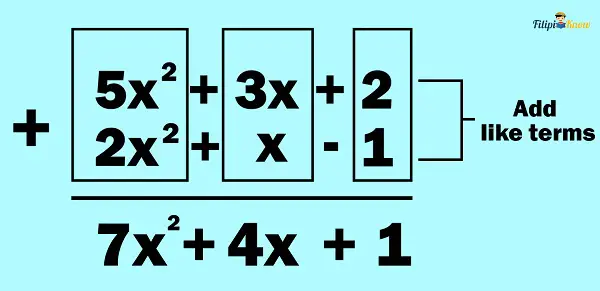
Thus, the answer is 7x² + 4x + 1.

Example 2: What is the sum if you add y² – 2z + x³, 5z – 3y + x², and 2x³ + 5y²?

Solution:

Step 1: Arrange the given polynomials in standard form. If we arrange the given polynomials into standard form, we will have the following:

x³ + y² – 2z

x² – 3y + 5z

2x³ + 5y²

Step 2: Place the like terms of the given polynomials in columns.

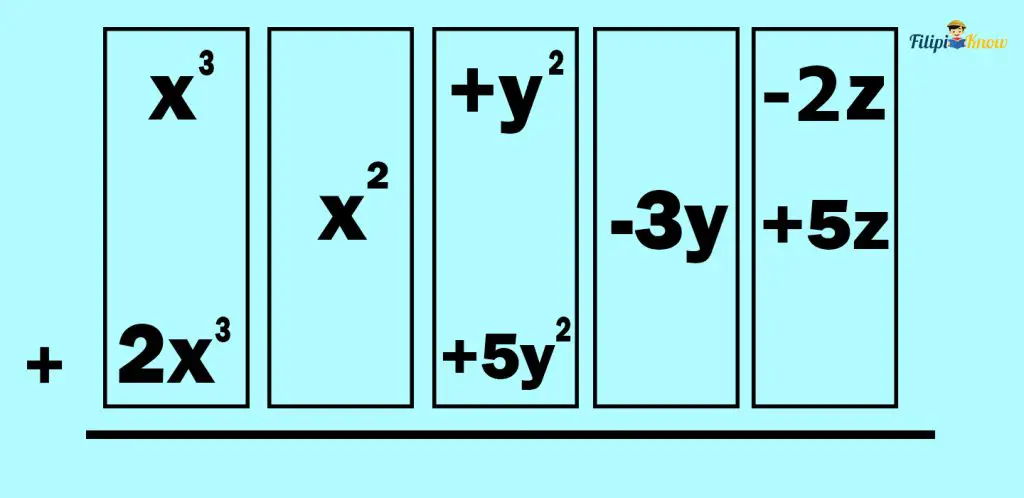
Step 3: Add the like terms.

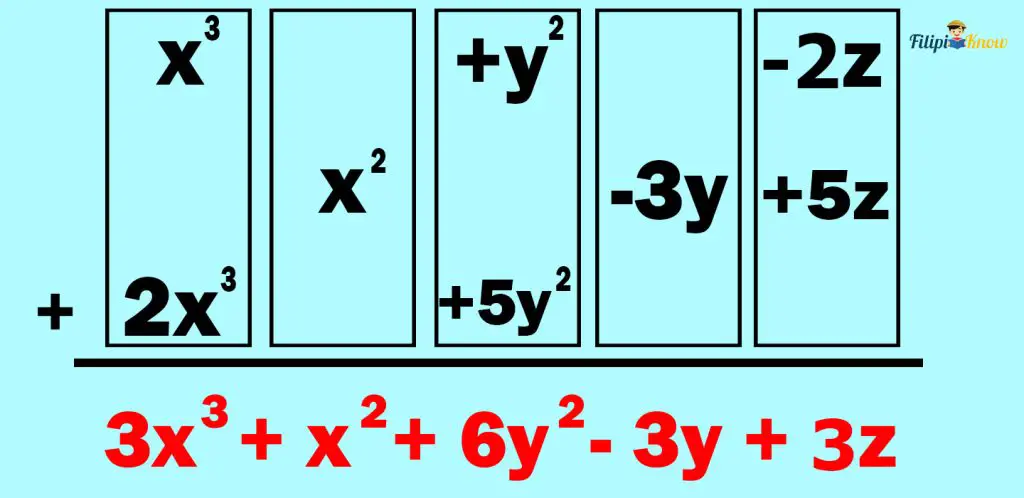
Therefore, the sum is 3x³ + x² + 6y² – 3y + 3z

Example 3: Add 62xy – 5x²y + 3 by -2x²y + 10xy – y + 5

Solution:

Step 1: Arrange the given polynomials in standard form. If we arrange the given polynomials into standard form, we will have the following:

-5x²y + 62xy + 3

-2x²y + 10xy – y + 5

Step 2: Place the like terms of the given polynomials in columns.

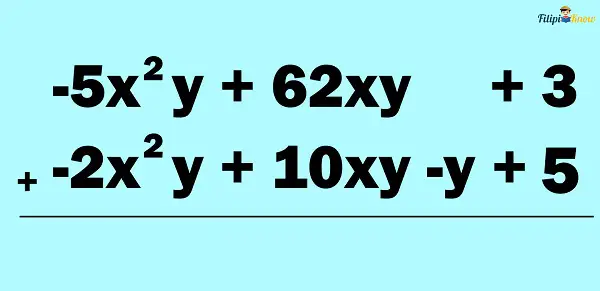
Step 3: Add the like terms. Do not forget the rules on operations on integers when dealing with signed numbers.

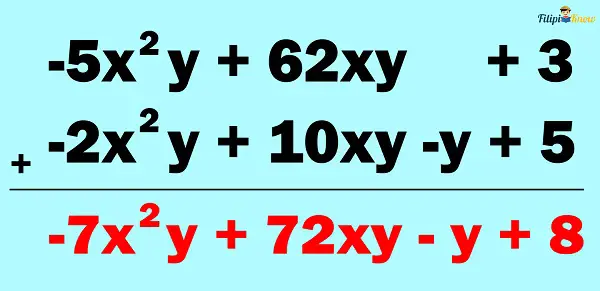
The answer is -7x²y + 72xy – y + 8.

 

2. Subtraction of Polynomials

To know how to subtract polynomials, follow these steps:

1. Write the given polynomials in standard form
2. Change the sign into addition and reverse the sign of each term of the subtrahend (or the second polynomial)
3. Add the polynomials 

Example 1: Subtract 8x² – 2x + 1 by 2x² – 5x – 7

Solution:

Step 1: Write the given polynomials in standard form. The given polynomials are already in standard form since their terms are arranged based on the decreasing exponent of the variables.

Step 2: Change the sign into addition and reverse the sign of each term of the subtrahend (or the second polynomial). The subtrahend in the given problem is 2x² – 5x – 7. If we switch the sign of each term of this polynomial, we have -2x² + 5x + 7. 

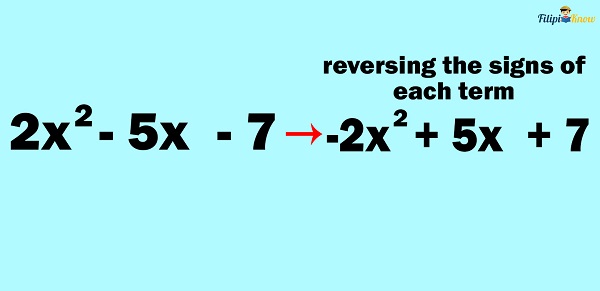
Step 3: Add the polynomials. We are now going to add 8x² – 2x + 1 to the polynomial we have obtained from step 2:

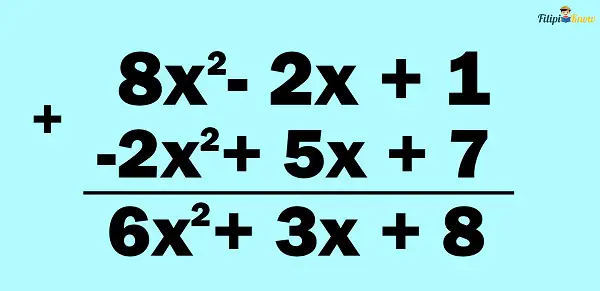
Hence, the answer is 6x² + 3x + 8.

Example 2: What is the difference between 7x⁵ – 5y + z² and 5x³ + 2x⁵ – 6x – 2z²?

Solution:

Step 1: Write the given polynomials into standard form. If we arrange the given polynomials into standard form, we will obtain the following:

7x⁵ + z² – 5y

2x⁵ + 5x³ – 2z² – 6x

Step 2: Change the sign into addition and reverse the sign of each term of the subtrahend (or the second polynomial). If we reverse the signs of each term of the second polynomial, we will obtain: -2x⁵ – 5x³ + 2z² + 6x

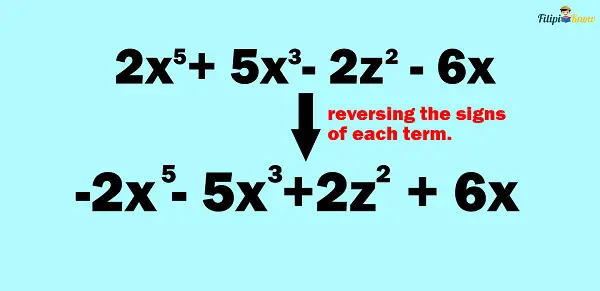
Step 3: Add the polynomials. We are now going to add 7x⁵ + z² – 5y to the polynomial we have obtained from step 2:

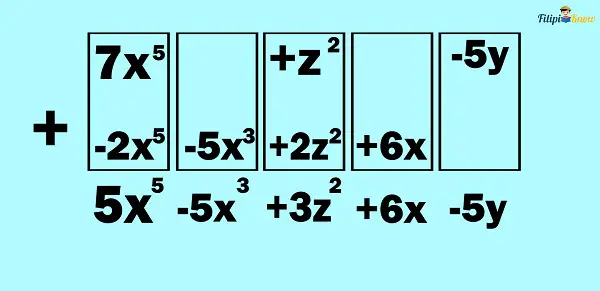
Hence, the answer is 5x⁵ – 5x³ + 3z² + 6x – 5y

 

3. Multiplication of Polynomials

When we multiply polynomials, we apply the distributive property of multiplication over addition (or simply distributive property). Before we start discussing how to multiply polynomials, let’s take a look first at what the distributive property is.

The distributive property tells us that multiplying the sum of two or more addends by a certain number equals the result when we multiply each addend by the same number.

In symbols,

a(b + c) = ab + ac

Example: Compute for 4(5 + 9).

Solution: If we use PEMDAS, we will obtain the following:

4(5 + 9)

4 (14)

  56

Thus, 4(5 + 9) = 56.

Now, let’s try to apply the distributive property:

4(5 + 9) = 4(5) + 4(9) = 20 + 36 = 56

Thus, by applying the distributive property, we obtain the following: 4(5 + 9) = 56.

Remember the concept of distributive property because we will apply this a lot when multiplying polynomials.

a. Multiplying a Polynomial by a Monomial

Let us start with the simplest one: How should we multiply a polynomial by a monomial?

Suppose we have the polynomial 5x² + 3x – 1 and want to multiply it by a monomial like 2x.

Let us express our problem above as a mathematical sentence:

(5x² + 3x – 1)(2x)

Since multiplication is commutative (changing the position of numbers in a multiplication process will not change the result), we can express it as:

(2x)(5x² + 3x – 1)

Take a look at our mathematical sentence above. Notice that we are multiplying a certain quantity (2x) by a sum of addends (5x² + 3x – 1). This means that we can apply the distributive property.

Applying the distributive property:

After ” distributing” 2x to the addends, we will perform multiplication. Note that we apply the laws of exponents (the product rule, in particular) when we multiply the same variables.

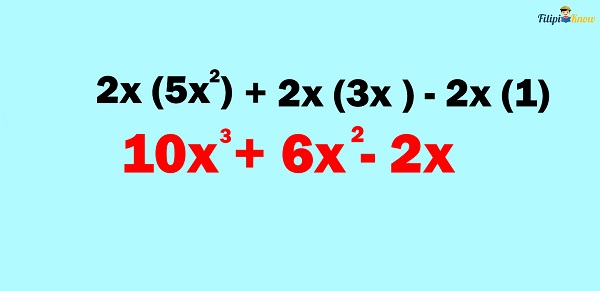
Therefore, (2x)(5x² + 3x – 1) = 10x³ + 6x² – 2x

Example: Multiply 8ab + 2a – 3c by 4ab

Solution: We have (4ab)(8ab + 2a – 3c). Applying the distributive property: 

(4ab)(8ab) +(4ab)(2a) – (4ab)(3c)

Performing multiplication to each term:

32a²b² + 8a²b – 12abc

Therefore, the answer is 32a²b² + 8a²b – 12abc

b. Multiplying a Polynomial by a Binomial

Suppose we have the polynomial 3p² + 2p – 1 and want it multiplied by a binomial such as 2p + 1. How can we multiply these expressions?

If we can express our given problem as a mathematical sentence, we have:

(2p + 1)(3p² + 2p – 1)

In this case, we can apply the distributive property. We can distribute the first term of the binomial, which is 2p, to 3p² + 2p – 1, and we can also distribute the second term of the binomial, which is 1, to the same polynomial (i.e., 3p² + 2p – 1). 

After we have distributed the terms of the binomial to the addends of the polynomial, we can apply again the distributive property:

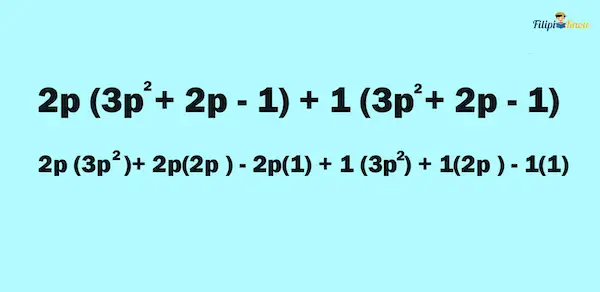
Perform multiplication to each term and apply the product rule.

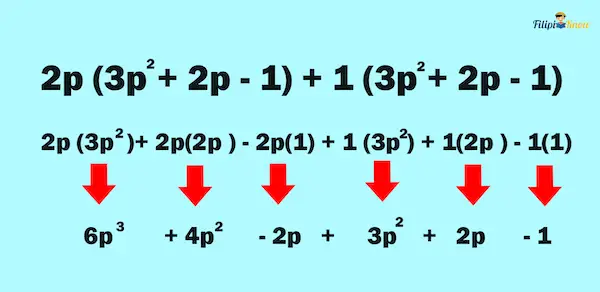
Note that we can combine some of the like terms of the resulting polynomial:

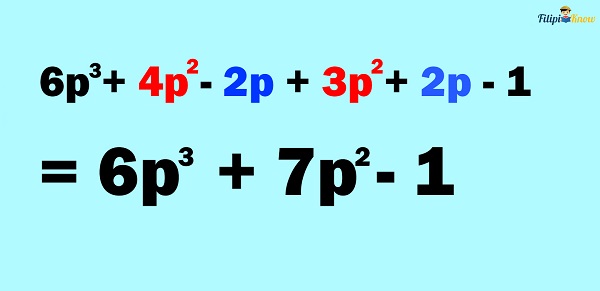
Therefore, the answer is 6p³ + 7p² – 1

Example: Multiply 5a² – 3ab + 2 by a – 2b

Solution: We have: (a – 2b)(5a² – 3ab + 2). Distributing each term of the binomial to the polynomial:

a(5a² – 3ab + 2) – 2b(5a² – 3ab + 2)

Applying the distributive property:

[a(5a²) – a(3ab) + a(2)] – [2b(5a²) – 2b(3ab) + 2b(2)]  

Multiplying each term:

[5a³ – 3a²b + 2a] – [10a²b – 6ab² + 4b]

We can rewrite the expression above as:

[5a³ – 3a²b + 2a] + [-10a²b + 6ab² – 4b]

Combining like terms:

5a³ – 13a²b + 6ab² + 2a – 4b

Therefore, the answer is 5a³ – 13a²b – 6ab² + 2a – 4b

c. Multiplying a Polynomial by Another Polynomial

You have learned how to multiply a polynomial by a monomial or a binomial in the previous sections of this review. Recall that we just applied the distributive property to multiply these expressions. Using the same technique, you can multiply a polynomial by another.

To multiply a polynomial by another, multiply each term of one polynomial by each term of the other polynomial and then combine like terms of the resulting polynomial.

Example 1: Multiply 3a² + 2a – 1 by a³ – 4a + 1.

Solution: Expressing the mathematical problem above as a mathematical sentence, we have:

(3a² + 2a – 1)(a³ – 4a + 1) 

We then multiply each term of 3a² + 2a – 1 to a³ – 4a + 1

Applying the principle of distributive property:

Putting together the terms and combining like terms:

Therefore, the answer is 3a⁵ + 2a⁴ – 13a³ – 5a² + 6a – 1.

Example 2: Multiply 5x²y + y + 2 by y² + 3x – 1

Solution: Expressing the mathematical problem above as a mathematical sentence, we have:

(5x²y + y + 2)(y² + 3x – 1)

We multiply each term of 5x²y + y + 2 to y² + 3x – 1:

5x²y(y² + 3x – 1) + y(y² + 3x – 1) + 2(y² + 3x – 1)

Applying the distributive property:

5x²y(y² + 3x – 1) + y(y² + 3x – 1) + 2(y² + 3x – 1)

        (5x²y³ + 15x³y – 5x²y) + (y³ + 3xy – y) + (2y² + 6x – 2)

Combining like terms and writing the resulting polynomial in standard form:

(5x²y³ + 15x³y – 5x²y) + (y³ + 3xy – y) + (2y² + 6x – 2)

   5x²y³ + 15x³y – 5x²y + y³ + 2y² + 3xy + 6x – y – 2

Therefore the answer is 5x²y³ + 15x³y – 5x²y + y³ + 2y² + 3xy + 6x – y – 2

The next chapter will discuss different techniques to multiply polynomials under different conditions. We call these techniques “special products.” This includes multiplying a binomial by another binomial, squaring a binomial, cubing a binomial, and so on.

 

4. Division of Polynomials

To divide polynomials, we use the long division method. This method allows us to use the division brackets used to divide whole numbers.

Suppose we want to divide 25x² + 10x – 15 by 5x + 5

25x² + 10x – 15 ÷ (5x + 5)

We first have to put  25x² + 10x – 15 inside the division bracket and then put 5x + 5 outside of it.

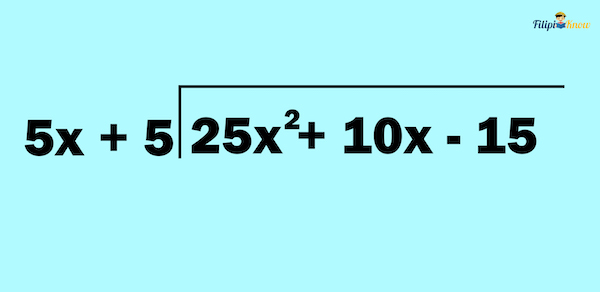
Next, we divide the first term of the polynomial inside the division bracket by the first term of the polynomial outside the division bracket. To perform this, we apply the quotient rule. We put the result above the bracket and aligned it to the first term of the polynomial inside the bracket.

We divide 25x² by 5x and obtain 5x. We then put this answer (i.e., 5x) above the division bracket, ensuring it’s aligned with the first term of the dividend.

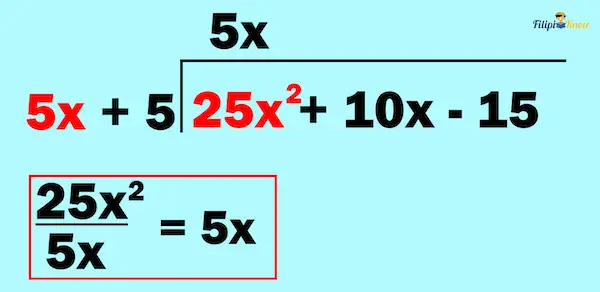
Then, we multiply the divisor by the answer we obtained earlier and subtract the answer from the dividend.

This means we multiply 5x + 5 by 5x to obtain 25x² + 25x. We then subtract 25x² + 25x from 25x² + 10x to obtain -15x. 

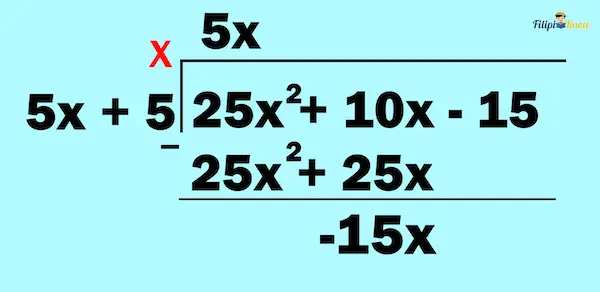
We bring down – 15 to create a new polynomial.

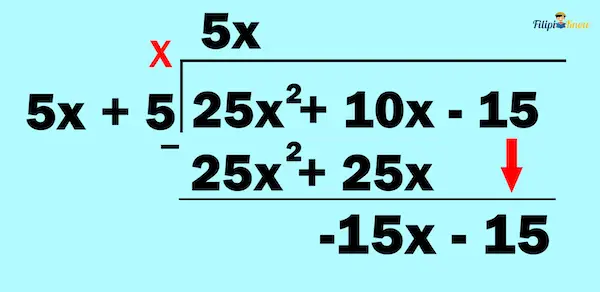
We repeat the things we performed above.

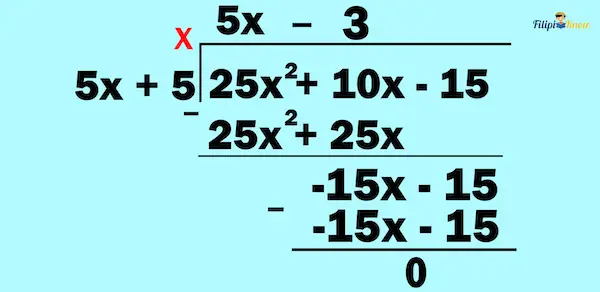
Hence, the answer is 5x – 3.

 

Next topic: Special Products and Factoring

Previous topic: Logarithms

Return to the main article: The Ultimate Basic Math Reviewer

 

Download Printable Summary/Review Notes

Download Printable Flashcards

Test Yourself!

1. Practice Questions [Free PDF Download]

2. Answer Key [Free PDF Download]

3. Math Mock Exam + Answer Key