Algebra is one of the oldest mathematical studies in human history. The ancient Egyptians and Babylonians used it to solve equations, approximate values, and explain geometric properties. From then on, algebra has become an indispensable tool in mathematics, physics, architecture, engineering, finance, and even social sciences.

Algebra is all about representing numbers and quantities using symbols or letters. It is like a puzzle where you have to unravel the value a particular symbol represents.

This review will introduce you to the foundation of the study of algebra through algebraic expression examples with answers.

Click below to go to the main reviewers:

Ultimate UPCAT Reviewer

Ultimate NMAT Reviewer

Ultimate Civil Service Exam Reviewer

Ultimate PMA Entrance Exam Reviewer

Ultimate PNP Entrance Exam Reviewer

Ultimate LET Reviewer

   

Variables and Constants

Let us start with the most fundamental terms in the algebra study – the variables and the constants.

1. Variables

Let me present to you a simple puzzle. In this puzzle, your goal is to determine what is the number being represented by the triangle. What do you think must be the number represented by the triangle?

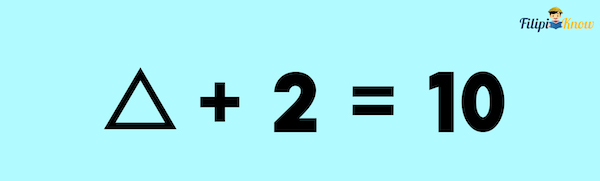
If you have answered 8, you got it right. The triangle represents the number 8 in the mathematical equation above.

The triangle used in our simple “puzzle” or equation above is an example of a variable.

A variable is a symbol that we use to represent a specific number. Again, the triangle is variable in our equation above since it represents the number 8. The variable is also called unknown since we have to solve the equation first so that we will be able to determine the value represented by the symbol.

Let us have another example:

Example 1: What do you think is the value of the banana in the equation below?

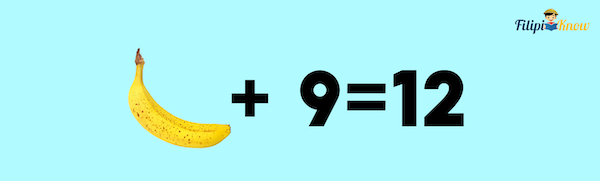
Solution: If your answer is three, you got our puzzle right. Now, can you determine the variable used in the equation above?

The banana acts as a variable since it represents the number three in the equation.

Again, a variable can be any symbol representing an unknown quantity or number. It can be a triangle, banana, square, circle, etc. However, an alphabetical letter is the most convenient way to represent an unknown quantity in a mathematical expression.

Let us retake a look at our example above, but this time, let us use a letter as a variable instead of a banana.

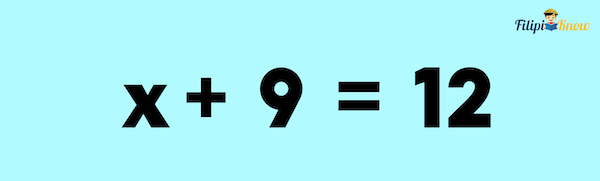
In this case, the letter x is a variable that represents the number 3.

Example 2: Look at the expression x + y + z + 3. What are the variables in the expression?

Solution: x, y, and z are the variables used in the expression x + y + z.

x, y, and z represent specific quantities or numbers.

Since a variable represents specific quantities or values, the value of a variable is not fixed. For instance, in x + y + z, the values of x, y, and z can be any number.

In the algebra study, English letters are the most commonly used variables. Thus, in this review, we will use letters to denote a variable representing a specific value.

2. Constants

A constant is a quantity with a fixed value. This means that the value of a constant does not change in the expression. For example, three is a constant since its value is always equivalent to 3, and it never changes once you include it in a mathematical expression.

It is important to note that all numbers are constants.

For example, in the expression x + 5, 5 is a constant because its value is always 5 in that expression, and it will never change. However, x is not a constant since its value is not fixed and specified and can be any number. 

3. Coefficients

If you multiply a variable by a specific number, the latter is called a numerical coefficient. Meanwhile, the variable becomes a literal coefficient.

Suppose we have a variable x which represents a certain quantity.

Now, our variable x is multiplied by 2. Thus, we have 2 × x. 

In algebra, when we multiply a variable by a specific number, we refrain from using the arithmetic sign for multiplication (×). Instead, we just put the variable and the constant together.

Therefore, when we multiply x by 2, we write it as 2x instead of  2 × x.

Now, please look at 2x. 2 is a numerical coefficient since it is the number multiplied by a variable. Meanwhile, x is a literal coefficient since it is a variable multiplied by a number.

Example 1: Determine the numerical coefficient and literal coefficient in ¼ y.

Solution: The numerical coefficient is ¼ since it is the number multiplied by the variable y. Meanwhile, y is the literal coefficient since it is a variable multiplied by a number.

If a variable has no number written on its left, the numerical coefficient is 1. For instance, consider the variable x. Note that there is no number written on its left. This does not mean that it has no numerical coefficient. Instead, its numerical coefficient is 1. Thus, x can also be interpreted as 1x or “1 times x”. 

However, in algebra, if the numerical coefficient is 1, we do not write it because it is already understood that a specific variable has a numerical coefficient of 1.

Example 2: Determine the numerical coefficient of the following:

1. 3y
2. 0.23x
3. w

Solution: For item 1, the numerical coefficient is 3. For item 2, the numerical coefficient is 0.23. Lastly, for item 3, the numerical coefficient is 1. 

 

Algebraic Expression

An algebraic expression is a mathematical expression that involves constants, variables, and arithmetic operations (addition, subtraction, multiplication, or division).

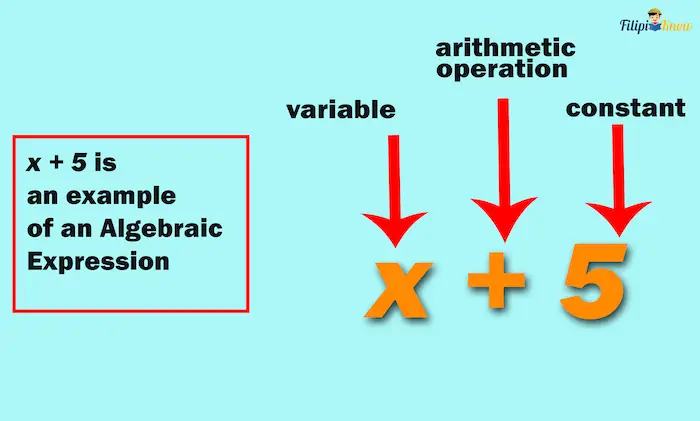
For example, x + 5 is an algebraic expression since it has a variable (which is x) that represents a certain quantity, a constant (which is 5), and an arithmetic operation (addition).

Another example, 3x – 9, is an algebraic expression where x is a variable, 9 is a constant, and the mathematical operations involved are multiplication (because 3x represents “3 times x”) and subtraction. Also, 3 is a numerical coefficient of x.

Example 1: Determine the variables, constant, coefficient, and operations involved in 9 + 3xy – z.

Solution: The variables are x, y, and z. The constant is 9. Meanwhile, the operations involved are addition, multiplication (3xy can be interpreted as 3 times x times y), and subtraction. Furthermore, 3 is a numerical coefficient of xy.

Example 2: Determine the variables, constants, and operations of the algebraic expression x⁄y – 2.

Solution: Before we answer this, note that in algebra, we usually indicate division as the ratio or a fraction between two numbers. Therefore, if we want to write x ÷ y, we write it as x/y instead. 

Therefore, in x/y – 2, the variables are x and y, the constant is 2, and the operations involved are division and subtraction.

Translating Verbal Expressions into Algebraic Expressions

You have already learned what algebraic expressions are. This section will teach you how to write an algebraic expression from an English sentence or phrase. This skill is crucial since you will solve word problems in the succeeding chapters.

Write “7 plus 4 equals 11” into a mathematical expression.

I know that you can translate that one with ease. The sentence “7 plus 4 equals 11” is simply: 7 + 4 = 11.

This is precisely what we will do in this section: Translate a sentence or phrase into a mathematical expression. But this time, we will be using variables and constants.

Having said that, let us try to translate this sentence into a mathematical expression:

“A number plus 4 equals 11”

The sentence is the same as the previous example above except for one thing. Notice that instead of stating 7, we replace it with the words “a number.”  How can we translate the given sentence into a mathematical expression?

Let’s find out the answer.

The word “a number” implies we are unsure what that number is. In other words, that number is unknown. For this reason, we need to use a variable that will represent this unknown number.

Recall that a variable is any symbol or letter representing an unknown number. Let us use the letter x to represent that unknown number in the given sentence.

Thus, we can translate the given sentence: “A number plus 4 equals 11” as:

 x + 4 = 11

And we’re done! We have already translated a verbal expression into an algebraic expression.

Example 1: Translate this verbal expression into an algebraic expression: “18 minus a number equals 5”.

Solution: The phrase “a number” means we are unsure what that number is. This means that we need to represent it using a letter or symbol. In other words, we need to use a variable to represent that unknown number.

Let us use the letter g to represent this unknown number. Thus, if we translate “18 minus a number is 5” into an algebraic expression, we will obtain the following:

18 – g = 5

Remember that you can use any letter in the English alphabet as a variable to represent a specific number. However, the most commonly used letters are x and y. Furthermore, small letters are more commonly used than capital letters. 

You now know how to use variables to translate verbal expressions into algebraic expressions. However, in your algebra study, you will encounter complicated sentences that are quite challenging to convert into algebraic expressions. For this reason, you need the help of keywords.

Keywords for Mathematical Operations

Keywords are words in a verbal expression that tell you what mathematical operations are involved in that sentence. They serve as your signals so that you can put the proper operations in the corresponding algebraic expression.

For instance, in our earlier example, “A number plus 4 equals 11”, the word “plus” is the keyword. It signals that you must use the addition sign (+) when you convert the given sentence into an algebraic expression.

This section will tackle some keywords that indicate the four fundamental mathematical operations.

1. Keywords for Addition

Some common keywords for addition are sum, plus, increased by, more than, and total. Once you see these keywords, it means that addition will be involved when you translate the verbal expression into an algebraic expression. 

The table below shows how these keywords are usually used in a sentence and how they can be translated into algebraic expressions.

Keyword	Example (Verbal Expression)	Algebraic Expression
sum	The sum of 8 and a number	8 + x
plus	-6 plus a number	-6 + x
increased by	A number increased by 7	x + 7
more than	3 more than a number	x + 3
total	The total of a number and -10	x + (-10)

The keywords sum and total are written before the given numbers. When you see these words, it means that the numbers are added. For example, the sentence “The sum of 8 and a number” implies that 8 and a certain number were added. Thus, the correct translation must be 8 + x.

The keyword increased by means that a certain number was added to another number. For instance, the sentence “A number increased by 7” means that 7 was added to a certain number. Thus, the correct translation must be x + 7.

Meanwhile, the keyword more than means the first number stated is added to the second number. For instance, the sentence “3 more than a number” implies that 3 was added to a certain number. Thus, when we translate it into an algebraic expression, we write 3 as the second addend since it is being added to a certain number. The correct translation should be x + 3. 

Example 1: Translate “the sum of two numbers” into an algebraic expression.

Solution: The given sentence doesn’t explicitly state the values of two numbers. Thus, we need to use variables to represent them. Let us use the letters x and y  to represent the numbers.

Since we have the keyword “sum,” the numbers must be added.

Thus, the sentence can be translated as x + y

The answer is x + y

Example 2: Translate “a number more than 18 is equal to 25” into an algebraic expression.

Solution: Let us assign k as the variable representing the sentence’s unknown number.

It’s stated that “a number more than 18 is equal to 25”. Since the keyword “more than” is used, it means addition is involved.

Again, the keyword “more than” implies that the first number mentioned in the sentence was added to the second number mentioned. This means that when we translate the sentence into an algebraic expression, we must write the second number, 18, as the first addend.

Thus, we can translate the sentence as 18 + k = 25.

The answer is 18 + k = 25.

2. Keywords for Subtraction

Words such as difference, subtracted by, subtracted from, deducted by, deducted from, decreased by, and minus are some of the keywords used for subtraction.

Keyword	Example (Verbal Expression)	Algebraic Expression
difference	The difference between a number and 15	x – 15
subtracted by	9 subtracted by a number	9 – x
subtracted from	9 subtracted from a number	x – 9
deducted by	15 deducted by a number	15 – x
deducted from	15 deducted from a number	x – 15
decreased by	A number decreased by 6	x – 6
minus	11 minus a number	11 – x

The keyword difference is the subtraction counterpart of the keyword sum. It is written before two numbers and implies that the given numbers were subtracted. Thus, if you have a sentence such as the difference between a number and 15, it is just x – 15.

The keywords subtracted by and subtracted from are quite confusing and should not be used interchangeably.

If the keyword subtracted by is used, it means the second number mentioned is the one being subtracted. For example, the given sentence 9 subtracted by a number means the unknown number was taken from 9. Thus, the correct translation is 9 – x.

On the other hand, the word subtracted from means the first number mentioned is the one being subtracted. For example, 9 subtracted from a number means 9 was taken from the unknown number. Thus, the correct translation is x – 9.

You can use this simple pattern if you still find it difficult to differentiate subtracted by and subtracted from:

Verbal Expression	Algebraic Expression
<First Number> subtracted by <Second Number>	<First Number> – <Second Number>
<First Number> subtracted from <Second Number>	<Second Number> – <First Number>

The words deducted by and deducted from work in the same way as the words subtracted by and subtracted from. Thus, you can use the table below (the same as above) for the words deducted by and deducted from.

Verbal Expression	Algebraic Expression
<First Number> deducted by <Second Number>	<First Number> – <Second Number>
<First Number> deducted  from <Second Number>	<Second Number> – <First Number>

Lastly, decreased by implies that the second number was subtracted from the first number. Hence, if the sentence “6 decreased by a number” is translated into an algebraic expression, we will obtain 6 – x.

Example 1: Translate “A number subtracted from – 19 is equal to 5” into an algebraic expression.

Solution: Let us use the letter p as the unknown number variable.

Recall that to translate a sentence with the keyword subtracted from into an algebraic expression, we will write it in the form <second number> – <first number>.

Hence, the correct translation must be: – 19 – p = 5.

Example 2: Translate “54 decreased by a number” into an algebraic expression.

Solution: Let us use the letter q to represent the unknown number.

The keyword “decreased by” implies that a number was subtracted from 54.

Thus, the correct translation should be 54 – q.

3. Keywords for Multiplication

Some keywords that indicate multiplication are product, multiplied by, twice, triple, of, and times.

Keyword	Example (Verbal Expression)	Algebraic Expression
product	The product of a number and 5	5x
multiplied by	-3 multiplied by a number	-3x
twice	Twice of a number	2x
thrice	Thrice of a number	3x
of	½ of a number	½x
times	7 times a number	7x

As a reminder, when we express the multiplication of a variable and a constant, we are no longer using the sign. Instead, we write the letter and the number together. For instance, if we want to write “8 times x,” we write it as 8x instead of 8 x.

The keyword “product” works in the same way as the keywords “sum” and “difference.” It is written before the given numbers and indicates that they were multiplied. For instance, if you want to translate “the product of 5 and a number” into an algebraic expression, the answer is 5x.

The keyword “multiplied by” tells you that the first number was multiplied by the second number. For instance, if you want to translate “– 3 multiplied by a number,” the answer is -3x.

The keyword “twice” means that the given number was multiplied by 2. For example, “twice of a number” means that a certain number was multiplied by 2. Hence, the answer is 2x.

The keyword “thrice” means that the given number was multiplied by 3. For example, “thrice of a number” means that a certain number was multiplied by 3. Hence, the answer is 3x.

The keyword “of” usually indicates a number multiplied by a fraction, a decimal, or a percent. For instance, “½ of a number” means multiplying a number by ½. Thus, the correct translation is ½x.

The keyword “times” tells you that the first number is multiplied by the second number in the sentence. For instance, the translation of “7 times a number: is simply 7x.

Example 1: Translate “20% of a number is equal to 50” into an algebraic expression.

Solution: The keyword “of” indicates multiplication. Thus, the correct translation is 20%x = 50. You can also express the given percent in decimal. This means that 0.20x = 50 is also a translation for the given sentence.

Example 2: Translate “The product of two numbers is equal to twice of another number” into an algebraic expression.

Solution: We have three unknown numbers involved. Thus, we need to use three letters as variables. Let us use the letters x, y, and z. 

The product of two numbers can be translated as xy. Meanwhile, since the keyword twice indicates that a number is being doubled or multiplied by 2, then twice of another number can be translated as 2z. Hence, the correct translation of the given sentence should be xy = 2z.

4. Keywords for Division

Some keywords that indicate division are quotient, divided by, the ratio of, split equally, and average.

Keyword	Example (Verbal Expression)	Algebraic Expression
quotient	The quotient of 8 and a number	8 ÷ x or 8⁄x
divided by	A number divided by 4	x ÷ 4 or x⁄4
ratio of	The ratio of a number and 2	x ÷ 2 or x⁄2
split equally	A number is split equally into 3	x ÷ 3 or  x⁄3

Recall that we can express the division of two numbers in fraction form. For example, we can rewrite 8 ÷ x as 8⁄x. The fractional form of the division of two numbers is usually used since writing is more convenient and less tedious when other operations are involved.

The keyword quotient is written before the given numbers and indicates that the operation of division is involved. For instance, the translation of “The quotient of 8 and a number” is 8 ÷ x or 8⁄x.

The keyword divided by implies that the first number mentioned in the sentence is the dividend while the second is the divisor. For example, if you want to translate “A number divided by 4”, the correct answer would be x ÷ 4 or x⁄4.

The keyword ratio of works the same way as the keyword quotient. It is written before the given numbers and indicates that the division operation is involved.  For example, the correct translation of “The ratio of a number and 2” is x ÷ 2 or x⁄2.

The keyword split equally works the same way as the keyword divided by. Thus, if we want to translate “A number is split equally into three,” the correct translation is x ÷ 3 or x⁄3.

Shown below is a summary of the keywords that are usually used for the four fundamental operations of mathematics:

Translating Verbal Expressions Into Algebraic Expressions with Multiple Operations Involved

We have translated various sentences or phrases into algebraic expressions. However, we have only translated those with only one mathematical operation involved. In this section, we will translate those involving multiple operations.

Ensure you still have the keywords in your mind because they are helpful in this section.

Example 1: What is “The sum of twice a number and 9” as an algebraic expression?

Solution: Let us start with the first keyword mentioned in the problem, the sum. Recall that if the keyword sum is used in a sentence, it implies that numbers are being added. The question is: What numbers are being added according to the verbal expression?

Let us repeat the verbal expression: The sum of twice a number and 9. It is clearly stated that two quantities will be added- twice a number and 9. 

We can now express our translation in this form for a while: twice a number + 9

Now, let us translate twice a number into an algebraic expression. Again, the word twice implies that a certain number is doubled or multiplied by 2. Let us use x to represent the unknown number. Thus, twice of x is 2x.

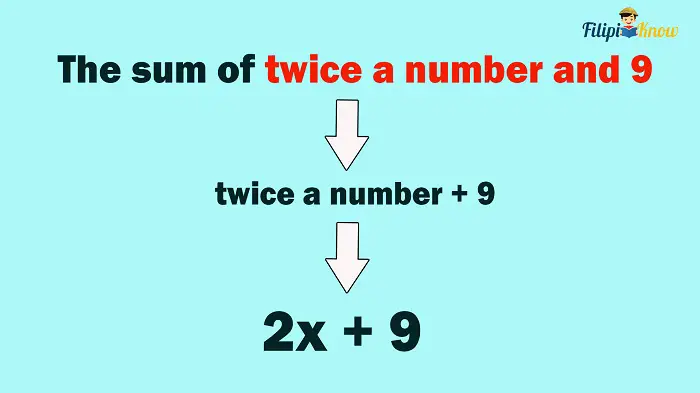
Therefore, our final translation for The sum of twice a number and 9 is 2x + 9.

Example 2: Translate “Twice the difference between two numbers” into an algebraic expression.

Solution: Let us start with the keyword twice. This keyword implies that a certain quantity or number will be multiplied by 2. What quantity will be multiplied by two according to the given verbal expression?

Read the given problem again: Twice the difference between two numbers. The statement tells us the difference between the two numbers is what will be multiplied by 2.

Hence, we can translate it this way: 2(difference between two numbers). We use parenthesis to indicate multiplication.

Now, let us translate the difference between two numbers into an algebraic expression. We have two unknown numbers, so let us use x and y to represent them. Thus, we can translate the difference between two numbers as x – y.

We replace the expression difference between two numbers in 2(difference between two numbers) with x – y.

Hence, Twice the difference between two numbers is 2(x – y).

Example 3: Write “the ratio of two numbers increased by 5” as an algebraic expression.

Solution: Let us start with the keyword ratio. The phrase the ratio of two numbers tells us that two numbers are involved in a division process. Let x and y be these two numbers. Hence, we can translate the ratio of two numbers as x ÷ y or x⁄y. For this problem, let us use x⁄y.

The following keyword increased by the ratio of two numbers increased by 5 tells us that 5 will be added to x⁄y. This means that we need to add 5 to our translation. Thus, 

 x⁄y+ 5

Therefore, if the ratio of two numbers increased by 5 will be written as an algebraic expression, you will have x⁄y+ 5

Other Important Keywords

More keywords are used in translating verbal expressions into algebraic expressions. Some of them involve exponents, radicals, equality, or inequality signs.

Here are other keywords commonly used that do not indicate any of the four fundamental operations:

1. Keywords for Radicals

Keywords for Radicals	Example (Verbal Expression)	Algebraic Expression
square root  cube root	The square root of a number  Cube root of a number	√x ∛x

2. Keywords for Exponents

Keywords for Exponents	Example (Verbal Expression)	Algebraic Expression
raised to square of cube of	A number raised to 5 Square of a number Cube of a number	x5 x2 x3

The keyword raised to tells us that a number has a specific exponent. The keyword square of means that a number is raised to the power of 2. Meanwhile, the keyword cube of means that a number is raised to the power of 3.

3. Keywords for Equality

Keywords for Equality	Example (Verbal Expression)	Algebraic Expression
equal to yields is	4 is equal to a number 3 plus a number yields 9 7 minus a number is 0	4 = x 3 + x = 9 7 – x = 0

4. Keywords for Inequality

Keywords for Inequality	Example (Verbal Expression)	Algebraic Expression
Not equal to Greater than Less than Greater than or equal to Less than or equal to At least At most	5 is not equal to a number 7 is greater than a number 7 is less than a number 0 is greater than or equal to a number 0 is less than or equal to a number 5 plus a number is at least 9 3 minus a number is at most 2	5 ≠ x 7 > x 7 < x 0 ≥ x 0 ≤ x 5 + x ≥ 9 3 – x ≤ 2

The keywords greater than or equal to is synonymous with at least. Meanwhile, the keywords less than or equal to are synonymous with at most.

Example 1: Write “the sum of the square of a number and 3 is at least 9” as an algebraic expression.

Solution: The keyword sum tells us that specific quantities will be added. These quantities are the square of a number and 3.

Let us use x to represent the unknown number. Its square can be represented as x².

Thus, the quantities that will be added are x² and 3. 

The sum of the square of a number and 3 is at least 9. This means that x²  + 3 is greater than or equal to 9.

Hence, the correct translation is x^2.+ 3 ≥ 9

Translating Verbal Expressions Into Algebraic Expressions in Real-Life Scenarios

We have now arrived at the most exciting part of this review. We will apply what we have learned in translating verbal expressions into algebraic expressions in various real-life scenarios.

Example 1: Lea has 150 books that she collected during her college years. She decided to give some of her books to her friends. After giving some to her friends, 40 books were left to Lea. Write an algebraic expression that will illustrate Lea’s scenario.

Solution: It’s stated in the given scenario that Lea has 150 books. She gave some of her books to her friends. Forty books were left to Lea after giving some of them. This can be interpreted as 150 books minus the number of books given equal 40.

Let us use b to represent the number of books Lea gave to her friends.

Thus, we have this algebraic expression: 150 – b = 40

Example 2: A burger costs ₱32 each, while a can of pineapple juice costs ₱25 each. Dario bought some burgers and cans of pineapple juice. Write an algebraic expression that shows how much Dario will pay for the burgers and cans of pineapple juice he bought.

Solution: The scenario does not explicitly state how many burgers and cans of pineapple juice Dario bought. Thus, we can use variables to represent the number of burgers and cans of pineapple juice he bought.

Let b represent the number of burgers that Dario bought. Meanwhile, let p represent the number of cans of pineapple juice that Dario bought.

Each burger costs ₱32. Thus, the total amount Dario will pay for the burgers can be represented as 32b.

Meanwhile, each can of pineapple juice costs ₱25. Thus, the total amount Dario will pay for the cans of pineapple juice can be represented as 25p.

Combining the total amount he will pay for the burgers and cans of pineapple juice: 32b + 25p.

Thus, the answer is 32b + 25p.

Translating Algebraic Expressions into Verbal Expressions

You have learned to translate a given sentence or phrase into algebraic expressions. This time, let us discuss translating a given algebraic expression into words or verbal expressions.

Translating an algebraic expression into a sentence or phrase has no general process. However, using the proper keywords helps perform the translation.

Example 1: Write x + 2 as a verbal expression.

Solution: The algebraic expression involves the operation of addition. Thus, you can use the keywords for addition in translating x + 2. Moreover, use the words “a number” to translate the variable.

Let’s use the keyword sum. We know that sum is written before the quantities that are added. Thus, one possible translation could be “the sum of a number and 2.”

Another possible translation is using the keyword “increased by.” You can translate x + 2 as “A number increased by 2”.

Example 2: Translate 4z + 5 into a verbal expression.

Solution: 4z indicates multiplication. Hence, you can use any keyword for multiplication. Let us use the keyword “product.” One possible translation for 4z is “the product of 4 and a number.”

Now, we incorporate the plus 5 in 4z + 5 to complete our translation. Hence, one possible translation is “the product of 4 and a number plus 5” Another possible translation could be “four times a number increased by 5”.

Example 3: Translate y² ≤ 2 into a verbal expression.

Solution: y represents a specific number. Thus, we can translate it as “a number.” Meanwhile, y² means that we squared that number. Hence, y² can be translated as “the square of a number.”

The symbol ≤ means less than or equal. We can use the phrase less than or equal for this symbol or the phrase at most. In this problem, let us use the phrase at most.

Therefore, one possible translation for y² ≤ 2 could be the square of a number is at most 2.

Evaluating Algebraic Expressions

We have mentioned that variables in an algebraic expression represent a specific number or quantity. What if the values that these variables represent are specified? Can we compute the value of the algebraic expression?

Evaluating an algebraic expression means determining its value according to the values assigned to its variables. To further understand how this works, let us have some examples.

Example 1: Evaluate x + 2 if x = 2

Solution: The variable in x + 2 is x. In this example, we have assigned a value to x: x = 2. This means that we need to substitute or replace x with 2.

Afterward, we calculate the algebraic expression’s value when x = 2.

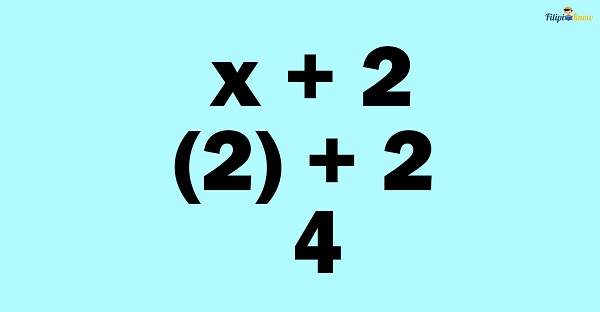
Thus, x + 2 = 4 if x = 2.

Example 2: Evaluate 5x + y if x = 2 and y = 0

Solution: We substitute 2 for x and 0 for y in 5x + y. Take note that 5x is the multiplication between 5 and x. Thus, once you substitute 2 for x, you will have 5(2), which implies “5 times 2”. 

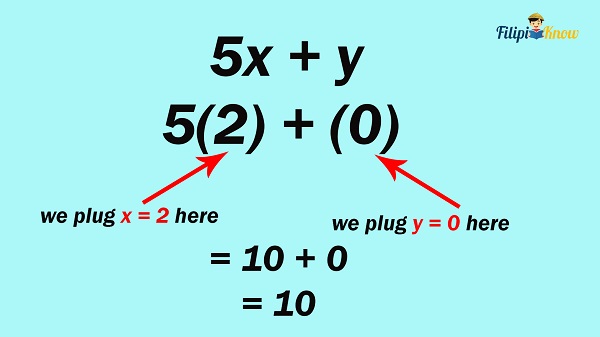
Hence, the answer is 10.

There are instances there is more than one mathematical operation involved when you evaluate an algebraic expression. In this case, to perform the computation, apply the order of operations or PEMDAS.

Example 3: Evaluate 2x – 3(y + z) if x = 10, y = 1, and z = 3

Solution: Plug in the assigned values for x, y, and z in the given algebraic expression:

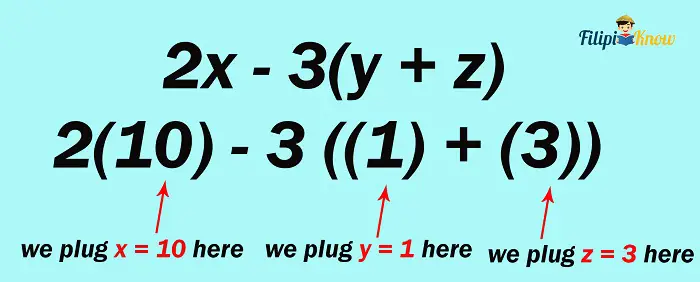
Since there are multiple operations involved, let us apply PEMDAS:

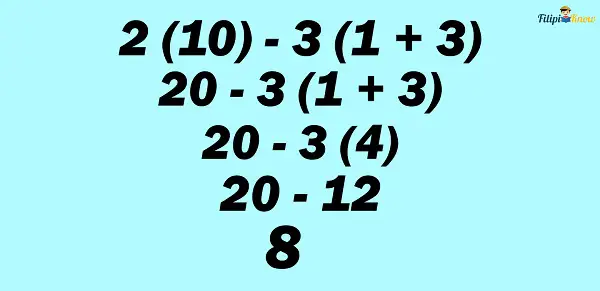
Therefore, the answer is 8.

Also, there are instances where the assigned values to the variables are real numbers and not just whole numbers. Thus, it is crucial that you still remember how to perform operations with integers, fractions, or decimals since variables can represent these numbers.

Example 4: Evaluate 8a – 3b if a = ½ and b = – 2

Solution: Let us add the values of a and b to the given algebraic expression.

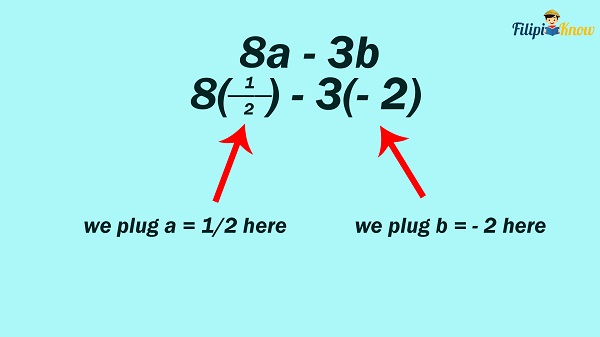
Performing the operations involved:

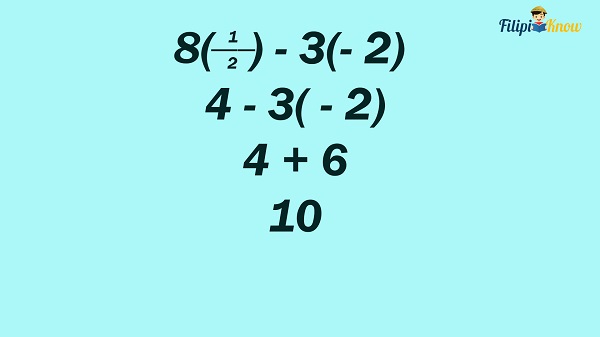
Thus, the answer is 10.

 

Next topic: Laws of Exponents

Previous topic: Ratio and Proportion

Return to the main article: The Ultimate Basic Math Reviewer

 

Download Printable Summary/Review Notes

Download Printable Flashcards

Test Yourself!

1. Practice Questions [Free PDF Download]

2. Answer Key [Free PDF Download]

3. Math Mock Exam + Answer Key