Percent is a great mathematical tool to express quantities and is used extensively in different things – from interest rates, discounts, and taxes to surveys, censuses, etc.

This article is your guide to percent and solving percent problems frequently appearing in major national examinations.

Click below to go to the main reviewers:

Ultimate UPCAT Reviewer

Ultimate NMAT Reviewer

Ultimate Civil Service Exam Reviewer

Ultimate PMA Entrance Exam Reviewer

Ultimate PNP Entrance Exam Reviewer

Ultimate LET Reviewer

What Does Percent Mean?

The word “percent” originated from the Latin phrase per centum, meaning “by hundred.” When we say “percent,” we refer to “parts per 100”. This means that a percent is a fraction with 100 as the denominator. The symbol % is used to indicate a percent.

For example, 3% means three parts per 100 or 3⁄100; 45% means 45⁄100; and 92% means 92⁄100.

Illustrating Percent

Suppose a vendor has 100 biscuits. If 10% of those biscuits are ube-flavored, 10⁄100 or 10 out of 100 biscuits are ube-flavored.

On the other hand, suppose there are 100 students in a school auditorium. If 42% of those students are honor students, 42⁄100 students, or 42 out of 100 students, are honor students.

Expressing Percent as Fraction and Decimal

Since percent means a fraction with 100 as the denominator, we can express a percent as a fraction or a decimal number.

Drop the percent sign and put 100 as the denominator to transform a percent into a fraction. For instance, 25% is simply 25⁄100.

Note that when 25⁄100 is reduced to its lowest terms, you will obtain ¼. This means that 25% is also equivalent to ¼. 

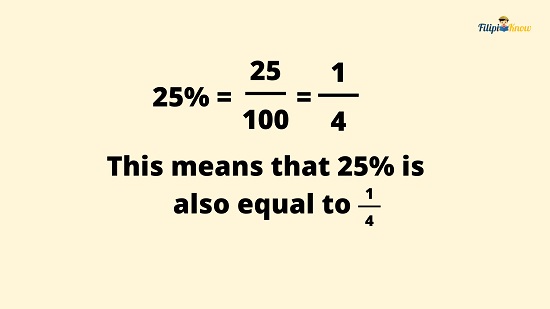
Furthermore, note that when you transform ¼ into its decimal form using the steps we have discussed in the previous reviewer, you will obtain 0.25. Hence, 25% is also equal to 0.25. 

There is an easier way to transform percent into decimals. Drop the percent sign and move the decimal point two places to the left of the given number.

For example, 54% is equivalent to 0.54

Example: Transform 3% to decimal form.

Solution:

Percentage

Suppose that your mom prepared ten pieces of your favorite cookies. You are excited to taste those cookies, but you realize that your brother ate 20% of the cookies that your mom prepared. What exactly is the number of cookies eaten by your brother?

To determine the answer to your question above, you must determine 20% of 10. This case involves the application of percentages.

The percentage is the result when you multiply a number by a percent. Returning to your problem about the number of cookies your brother ate, 20% of 10 can be determined if you multiply ten by 20%. The result after you multiply the numbers is called the percentage.

How To Find the Percentage

Follow these steps if you want to find the percentage:

Step 1: Convert the given percent (the one with the % sign) into decimals.

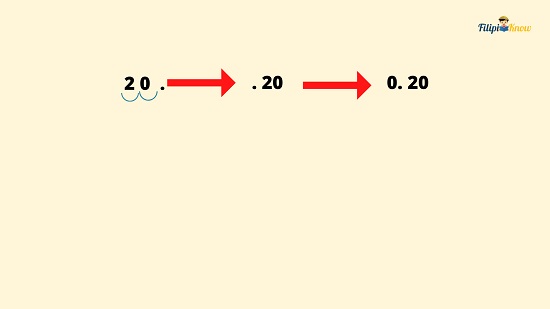
Again, to convert percent into its decimal form, we drop the percent sign and then move the decimal point two places to the left. Thus, 20% = 0.20

Step 2: Multiply the decimal you have obtained from Step 1 to the given number. The result is the percentage.

To multiply 0.20 by 10, we ignored the decimal point for a while and multiplied the given decimals like whole numbers. We have obtained 0200. Since 0.20 has two decimal places while 10 has none, the final answer should have two decimal places. We count two digits from the right of 0200 and put the decimal point there. Hence, the answer is 02.00, which is equivalent to 2.

Hence, 20% of 10 is 2. This means that out of 10 cookies your mother prepared, 2 of those were eaten by your brother.

Let us have another example.

Example: What is 50% of 120?

Step 1: Convert the given percent (the one with the % sign) into decimals.

We drop the % sign of 50% and move the decimal point two places to the left.

Thus, 50% = 0.50

Step 2: Multiply the decimal you have obtained from Step 1 to the given number. The result is the percentage.

To multiply 0.50 by 120, we ignored the decimal point for a while and multiplied the given decimals like whole numbers. Through this process, we have obtained 06000. Since 0.50 has two decimal places while 120 has none, the final answer should have two decimal places. We count two digits from the right of 06000 and put the decimal point there. Hence, the answer is 060.00, which is equivalent to 60.

Hence, 50% of 120 is 60.

Simple Tricks in Computing Percentages

We always want to make our computations in mathematics faster and more accurate. For this reason, I will share two tricks you can use when computing percentages.

Trick #1: You can compute some percentages using only mental computation.

If you want to determine the 25%, 50%, 75%, or 100% of a number, you can do so without the help of pen and paper.

• 25% is equivalent to 25⁄100 or ¼. Hence, to find the 25% of a number, divide the given number by 4. Example: 25% of 40 is just 40 ÷ 4 = 10.
• 50% is equivalent to 50⁄100 or ½. Thus, to find the 50% of a number, divide the given number by 2. This means 50% of a number is just half the given number. Example: 50% of 40 is just 40 ÷ 2 = 20.
• 75% is equivalent to 75⁄100 or ¾. Thus, to find the 75% of a number, multiply the given number by three and then divide the result by 4. Example: 75% of 40 is just 40 x 3 = 120 ÷ 4 = 30.
• 100% is equivalent to 100⁄100 or 1. Thus, 100% of a number is the number itself. Example: 100% of 40 is just 40 itself.

Trick #2: X% of a number Y is equal to Y% of number X

This trick means we can transfer the % sign to the other number, and the result will be the same.

Example: What is 40% of 25?

Using trick #2, we can transfer the % sign from 40% to 25. Thus, we have 25%. This means 40% of 25 is the same as 25% of 40.

Thus, applying our first trick on finding the 25% of a number, 40 ÷ 4 = 10; hence, 40% of 25 is 10.

Example: What is 92% of 50? 

92% of 50 is the same as 50% of 92. Hence, we can just divide 92 by 2 to obtain the answer, 92 ÷ 2 = 46

Therefore, 92% of 50 is 46.

Base and Rate

The base is the amount you are taking a percent of. Meanwhile, the rate is the percent you are calculating.

For example, if there are 50 students in a classroom and 20% of those students are honor students, it follows that ten students are honor students. 50 is the base since it is the amount we take a percent of. Meanwhile, 20% is the rate since we calculate the percentage. Lastly, 10 is the percentage.

The product of the base and the rate is the percentage.

Percentage = Base × Rate

Example: Determine the percentage, base, and rate if 20% of 90 is 18.

Solution: 

Since 90 x 20% = 90 x 0.20 = 18, 90 is the base, 20% is the rate, and 18 is the percentage.

Calculating Percentage, Base, and Rate

Formula to Find the Percentage

The formula to find the percentage, as we have stated, is: 

Percentage = Base × Rate

We can manipulate the mathematical equation above to obtain the formulas for computing the base and the rate:

Formula to Find the Base

Base = Percentage ÷ Rate

Formula to Find the Rate

Rate = Percentage ÷ Base

Example 1: If 10% of a number is 90, what is the number?

Solution:

We can interpret this question as 10% of ______ = 90. Since “of” is a signal word for multiplication, it also implies 10% x ______ = 90

This means that 10% is the rate while 90 is the percentage. The unknown number is the base. Thus, we need to compute the base.

Using the formula to find the base:

 Base = Percentage ÷ Rate

Base  = 90 ÷ 10%

Convert the given percent into decimal:

Base  = 90 ÷ 0.10

Now that you have already transformed the rate into decimal form, you may divide 90 by 0.10 to obtain the answer.

To perform division with decimal numbers, we need to transform the divisor (0.10) into a whole number by moving two decimal places to the right. Thus, the new divisor is 10. We also move two decimal places for the dividend (90). Thus, the new dividend is 9000.

We now perform long division with our new dividend and divisor:

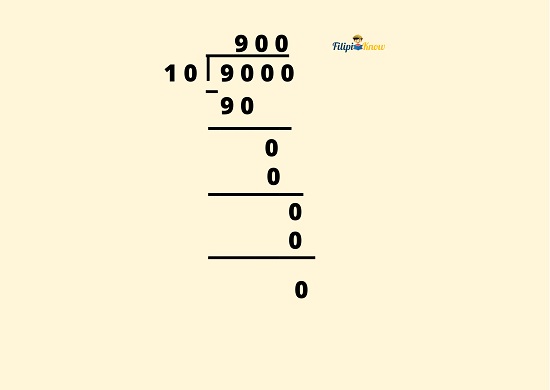
To find the base, we compute 90 ÷ 0.10 = 900

Hence, the base is 900.

Example 2:  What percent of 720 is 90?

Solution:

We can translate the question above in this form: _____% of 720 is 90 or _____% x 720 = 90. Therefore, 720 is the base, while 90 is the percentage. The missing number is the rate.

We will now use the formula for finding the rate.

Rate = Percentage ÷ Base

Again, based on the given problem, the percentage is 90 while the base is 720

          Rate = 90 ÷ 720

Notice that the dividend (the first number) is smaller than the divisor (the second number). In this case, you may apply the same steps in transforming fractions into decimal form because  90 ÷ 720 is a proper fraction (i.e., 90⁄720).

Let us divide 90 by 720 using the steps in transforming fractions into decimal form.

We add some zeros and decimal points to proceed with the division process.

We can now divide 900 by 720.

Note that every time the remainder becomes smaller than the divisor, we add zeros to 900 and the remainder to continue the division process.

The quotient we obtained is 0.125. Thus, 0.125 is our rate.

However, the rate must always be expressed with a percent sign. To do this, we multiply 0.125 by 100 or move two decimal places to the right of it and put a percent sign. Thus, 0.125 is equal to 12.5%.

Therefore, the rate is 12.5%

The Percentage, Base, and Rate Triangle

What if you forgot the formula to determine the percentage, base, or rate in a particular problem? Don’t worry because there is a fun way to derive these formulas. 

Shown below is the Percentage, Base, and Rate Triangle. It is a triangle divided into three portions where P (for percentage) is written on the upper portion, and B (for base) and R (for rate) are written on the lower portions. There are also division signs in the triangle’s outer left and outer right parts and a multiplication sign below it.

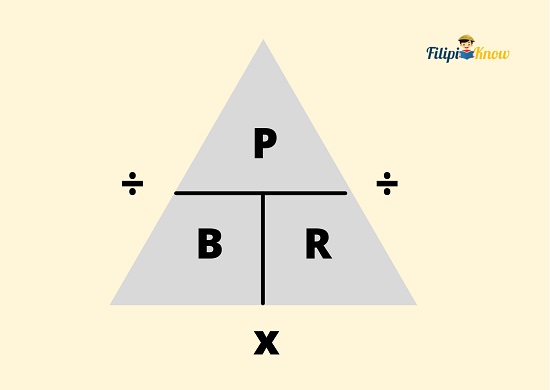
How To Use the Percentage, Base, and Rate Triangle

Suppose you are looking for the base. You have to cover the B in the triangle and look at the remaining letters and the operation between them. Notice that if you cover B, the remaining letters are P and R, with a division sign between them. This means that to find the base, you must divide P by R.

Next topic: Ratio and Proportion

Previous topic: Fundamental Operations on Fractions and Decimals

Return to the main article: The Ultimate Basic Math Reviewer

Download Printable Summary/Review Notes

Download Printable Flashcards

Test Yourself!

1. Practice Questions [Free PDF Download]

2. Answer Key [Free PDF Download]

3. Math Mock Exam + Answer Key