We may have mastered comparing objects descriptively, but how do we mathematically compare objects?

The answer is through ratio.

The ratio is the mathematical tool we use to compare quantities using division. The concept of ratios leads to the concept of proportions, which has a lot of applications in our daily lives. For example, when we convert currencies, estimate the volume of gasoline required for a car to cover a certain distance, calculate the cost of items bought, and so on.

This article features ratio and proportion examples with answers to help you effectively learn these concepts and how to apply them in your daily life.

Click below to go to the main reviewers:

Ultimate UPCAT Reviewer

Ultimate NMAT Reviewer

Ultimate Civil Service Exam Reviewer

Ultimate PMA Entrance Exam Reviewer

Ultimate PNP Entrance Exam Reviewer

Ultimate LET Reviewer

   

Ratio

A ratio shows how an object’s quantity is related to another object’s quantity. For example, if there are 15 male and 23 female students in a classroom, we can compare these quantities using a ratio, particularly 15 : 23.

We usually write it in the format below to express two quantities being compared as a ratio. Note that we use a colon (:) to express a ratio.

<first number> : <second number>

Example: Aling Bela has 4 chickens and 8 pigs on her small farm. What is the ratio of her chickens to her pigs?

Solution: We can express the ratio of chickens to pigs that Aling Bela owns as 4 : 8

Ratio as a Fraction

We can write a ratio into its equivalent fractional form. We write the first number as the numerator, then the second as the denominator.

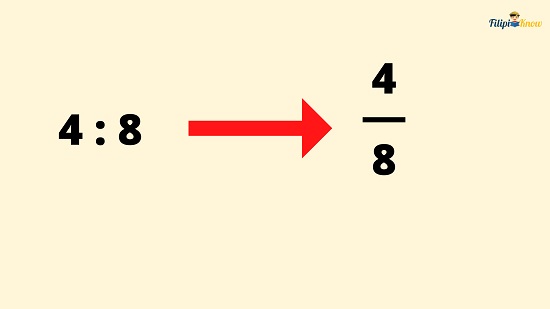
For instance, using our example above about Aling Nena’s chickens and pigs, we can express the ratio of her chickens to her pigs (i.e., 4 : 8) as 4⁄8.

Example 1: For every 4 burgers you buy, you must pay ₱128. What is the ratio of the number of burgers bought to the price you must pay? Express the ratio in fractional form.

Solution: We can express the ratio of the number of burgers bought to the price you must pay as 4 : 128. In fractional form, we can write this as 4⁄128.

Example 2: There are 15 science teachers in a public high school. In that same high school, there were 10 math teachers. What is the ratio of science teachers to math teachers in that public high school? Express the ratio in fractional form.

Solution: We can express the ratio of science teachers to math teachers in that public high school as 15 : 10. In fractional form, we write it as 15⁄10.

Using Ratio to Compare a Part to a Whole

We have already defined what ratios are. However, the ratios that we tackled in our previous sections pertain to comparing an object’s quantity to a different object’s. 

This time, let us use the ratio to compare a part of a whole to the whole itself.

Suppose you and your friends bought a pizza and sliced it into 8 equal parts. Suppose that you’re able to take 2 slices from it. What is the ratio of the slices of pizza you have (a portion of the whole pizza) to the total number of slices (the whole pizza)?

The given situation above might ring a bell to you. Yes, we can use fractions to show that comparison. In particular, fraction 2⁄8 can be expressed as 2 : 8.

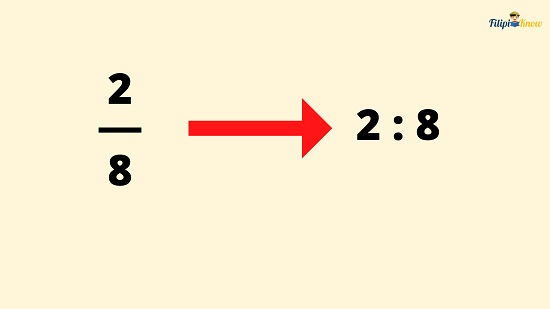
This means that to use the ratio to compare a part of a whole to the whole itself, we can use this format:

<portion of the whole> : <total number portions of the whole>

Example: In a classroom, 15 students are male while 20 are female. What is the ratio of female students to the total number of students in the classroom?

Solution: There are 20 female students in the classroom. Meanwhile, the total number of students in the classroom is the sum of the number of male students and the number of female students. There are 15 + 20 = 35 students in that classroom.

Therefore, the ratio of female students to the total number of students in that classroom can be expressed as 20 : 35

 

Proportion

A proportion indicates that the two ratios are equal. In other words, proportions are equivalent ratios. Hence, if we say that ratios are proportional, we mean that those ratios are equal in value.

Let’s say we have two ratios, 1 : 2 and 2 : 4. We illustrate these ratios as shown below:

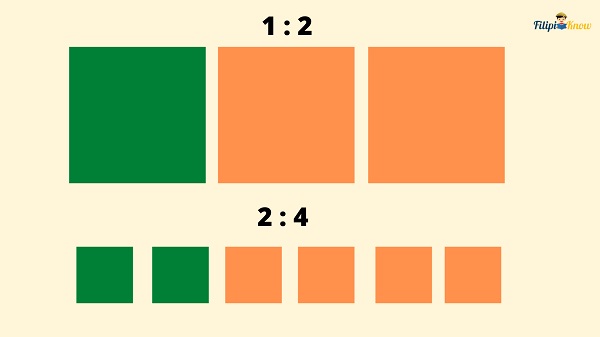
It’s seen that the ratios represent the same parts. It implies that these ratios are equivalent.

Hence, 1 : 2 = 2 : 4 is a proportion.

You might have realized that proportions are similar to the concept of equivalent fractions. Indeed, proportions indicate equivalent fractions since we can write ratios in fractional form.

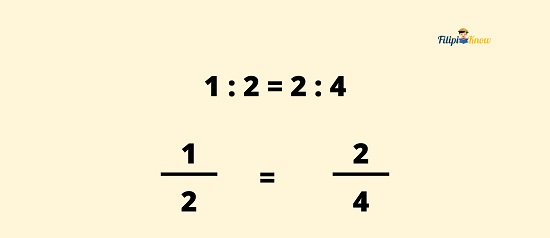
How to Know if Two Ratios Are Proportional

Two ratios are proportional if they are equal. One way to determine if two ratios are equal is by converting them into fractional form and using the cross-multiplication method we discussed in the Fractions and Decimals review.

For instance, let us use the cross-multiplication method to determine if 1 : 2 = 2 : 4 is proportional.

Since the products are equal (both equal to 4), the ratios are equal. Hence, the ratios are proportional.

Moreover, you might also notice that if we multiply the numbers in a ratio, we can obtain another ratio that is proportional to that ratio. 

For example, if we multiply each number in 5 : 2 by the same number, let’s say 2, we have 10 : 4. Using the cross-multiplication method, you can verify that 5 : 2 = 10 : 4

Example: Give a ratio that is equivalent or proportional to 2 : 9

Solution: We can determine a ratio equivalent to or proportional to 2 : 9 by multiplying each number in 2 : 9 by the same number.

Let us try to multiply the numbers in 2 : 9 by 5.

(2 x 5) : (9 x 5) = 10 : 45

Hence, 2 : 9 = 10 : 45. 

Note: The number you can use to find a proportional ratio to 2 : 9 is arbitrary.  If we multiply the numbers in 2 : 9 by the same number, we will come up with a ratio that is proportional to 2 : 9. In this example, I just arbitrarily used 5. You may use any number and multiply it by the numbers in 2 : 9, and you will come up with a ratio that is proportional to it.  For example, I can multiply the numbers of 2 : 9 by 7 and obtain 14 : 63. 14 : 63 is also proportional to 2 : 9

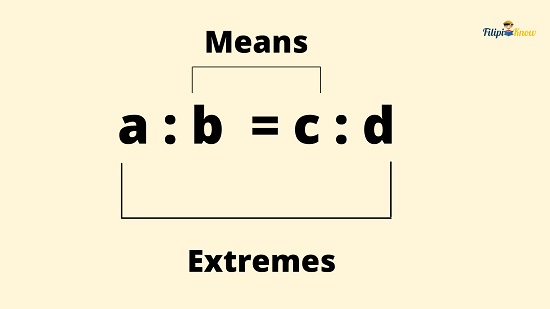
Parts of a Proportion: Extremes and Means

Suppose a proportion a : b = c : d where a, b, c, and d represent real numbers.

The proportion’s first and last terms (i.e., a and d) are called the extremes. Meanwhile, the second and third terms (i.e., b and c) are called the means.

Example: Determine the extremes and the means of the proportion 5 : 10 = 20 : 40

Solution: The extremes are the first and last terms of the proportion, which are 5 and 40, respectively. Meanwhile, the means are the second and third terms of the proportion, which are 10 and 20, respectively.

Properties of Proportion

Using the fact that proportions are equivalent ratios, we can mathematically derive their properties. These properties are beneficial when solving problems involving ratios and proportions.

Here are the properties of proportion:

Property #1: The Product of the Means Is Equal to the Product of the Extremes

For every proportion a : b = c : d, then a x d = b x c

This property tells us that we will obtain the same number if we multiply the means and the extremes of a proportion.

For example, suppose the proportion 4 : 3 = 12 : 9. 

If we multiply the means: 3 x 12 = 36

If we multiply the extremes: 4 x 9 = 36

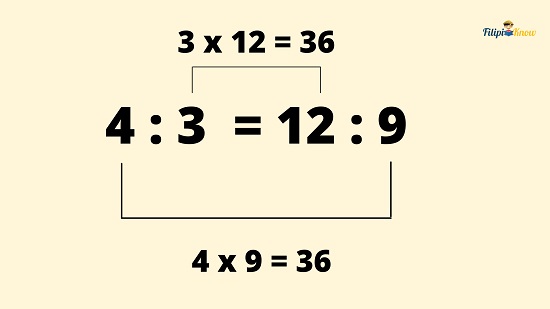
Note that the products of the means and the extremes equal 36.

Example 1: What must be N so that N : 8 = 2 : 16 is a proportion?

Solution: Let us use the fact that the product of the means of a proportion equals the product of the extremes.

Multiplying the means, we have: 8 x 2 = 16

Multiplying the extremes, we have 16 x N 

Now, by the first property, 16 x N = 16. What must be multiplied by 16 so that it will be 16? That number should be 1.

Hence, N = 1.

Therefore, the proportion should be 1 : 8 = 2 : 16.

Example 2: Four kilos of chicken cost ₱640. How many kilos of chicken can you buy with ₱3200?

Solution: The ratio of the kilos of chicken that can be bought to the cost is 4 : 640. Now, let’s use N to represent the number of kilos of chicken that can be bought with ₱3200. Thus, we have the ratio N : 3200.

4 : 640 = N : 3200

Let us apply that the product of the means is equal to the product of extremes so we can determine N.

Multiplying the means of the ratio: 640 x N 

Multiplying the extremes of the ratio: 4 x 3200 = 12800

Since the product of the means is equal to the product of the extremes:

640 x N = 12800

What must be multiplied by 640 to obtain 12800? We determine that number by dividing 12800 by 640.

N = 12800 ÷ 640 = 20

Therefore, you can buy 20 kilos of chicken for ₱3200.

Property #2: The Reciprocals of the Ratios in a Proportion Are Equal

Recall that the reciprocal of a fraction is its multiplicative inverse or simply the same fraction but with the positions of the numerator and the denominator reversed.

For example, the reciprocal of ⅖ is 5⁄2.

Given a proportion, say a : b = c : d, we can express it in fractional form as a⁄b = c⁄d

If we get the reciprocal of both fractions in a⁄b = c⁄d, we have:

 b⁄a = d⁄c

We can express  b⁄a = d⁄c in ratio as b : a = d : c

This property states that if we take the reciprocal of each ratio in proportion, the ratios are still proportional. In symbols:

a : b = c : d → b : a = d : c

Example: If 5 : 4 = 35 : 28, what should be N so that 4 : 5 = 28 : N

Solution: Since the ratios in the proportion are reciprocated, we can use the second property of proportions. Using the second property, N = 35.

Property #3: Switching the Means or the Extremes in a Proportion Will Result in a Proportion

Suppose the proportion 1 : 7 = 3 : 21. If we try to switch the positions of the means of this proportion, we have 1 : 3 = 7 : 21. You can verify using cross-multiplication that 1 : 3 = 7 : 21 is true (that is, 1 : 3 and 7 : 21 are equivalent ratios or proportional).

Now, let us try switching the extremes of 1 : 7 = 3 : 21. We obtain 21 : 7 = 3 : 1. Again, you can verify using cross-multiplication that 21 : 7 = 3 : 1 is true.

Hence, for every proportion a : b = c : d, switching the means or the extremes will still result in a proportion.

a : b = c : d → a : c = b : d and d : b = c : a

Example: When A is divided by 5, the result will equal the result when you divide B by 2. What is the result if you divide A by B?

Solution: The problem sounds tricky since we have no idea what the values of A and B are. However, we can determine the result by dividing A by B using the third property of proportion.

A divided by five can be written as A⁄5, which can then be expressed into a ratio of A : 5.

Meanwhile, B divided by 2 can be written as B⁄2, which can then be expressed into a ratio of B : 2.

Since the problem states that if A is divided by 5, the result will be equal to the result if B is divided by 2, then 

A : 5 = B : 2

We want to know what will be the result when we divide A by B or A⁄B or, as a ratio, A : B

So, from A : 5 = B : 2, how can we obtain A : B?

We can apply the property that if we switch the means of a proportion, the result is still a proportion.

Let us now switch the means of A : 5 = B : 2

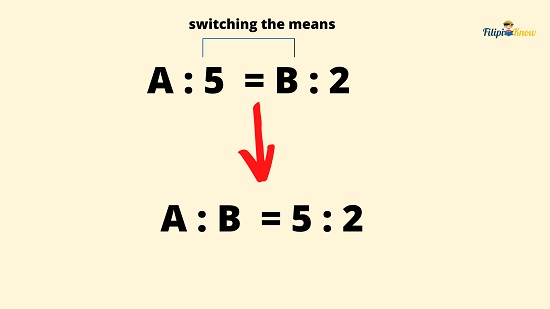
We obtain A : B = 5 : 2. Expressing into a fractional form:

A⁄B = 5⁄2

Therefore, if A is divided by B, the result is 5⁄2 or 2.5.

 

How To Solve Problems Involving Ratio and Proportion

In this section, let us try to solve some real-life word problems that can be solved using the concepts of ratio and proportion.

Problem 1: Suppose that on a specific date, 1 US dollar equals ₱50. How many US dollars is equivalent to ₱650?

Solution: The ratio of US dollars to the Philippine Peso can be expressed as 1 : 50. Let N be the number of dollars we can obtain from ₱650.

Hence, we have this proportion: 1 : 50 = N : 650

The product of the means is equal to the product of extremes. Thus:

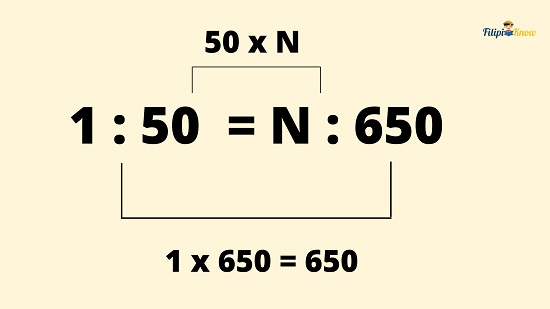
What must be multiplied by 50 to obtain 650? 

N = 650 ÷ 50 = 13

Therefore, ₱650 is equal to 13 US dollars.

Problem 2 : Leonor loves animals. He has a lot of dogs and cats in his house. The ratio of dogs to his cats is 1 : 3. The total number of dogs and cats is 8. How many cats does Leonor own?

Solution: The ratio of dogs to cats is 1 : 3. This doesn’t mean Leonor has 1 dog and 3 cats. 1 : 3 is just a ratio used to compare the number of dogs to cats. To find Leonor’s actual number of dogs and cats, we need to find two numbers with a sum of 8 that, when expressed as a ratio, will be proportional to 1 : 3.

Recall that we can obtain a ratio proportional to 1 : 3 if we multiply 1 and 3 by the same number.

Let us multiply the parts of the ratio with a number a.

(1 x a) : (3 x a) 

This means that we have two numbers, 1 x a and 3 x a. 1x a represents the total number of dogs Leonor has, while 3 x a represents the total number of cats Leonor has.

Since the total number of dogs and cats that Leonor has is 8:

(1 x a) + (3 x a) = 8

We can simplify the expression above as:

(4 x a) = 8

What must be multiplied by 4 to obtain 8? Simple, that number must be 2.

Hence, a = 2.

Recall that 1 x a represents the number of dogs Leonor has; since we have computed that a = 2, Leonor has 1 x (2) = 2 dogs.

We are doing the same thing to find Leonor’s number of cats: 3 x (2) = 6.

Therefore, Leonor has six cats.

 

Next topic: Algebraic Expressions

Previous topic: Percentage

Return to the main article: The Ultimate Basic Math Reviewer

 

Download Printable Summary/Review Notes

Download Printable Flashcards

Test Yourself!

1. Practice Questions [Free PDF Download]

2. Answer Key [Free PDF Download]

3. Math Mock Exam + Answer Key