In the previous chapters, you encountered quantities with exponents that are integers (i.e., 0, positive whole numbers, and negative whole numbers). This time, we will explore the realm of quantities with exponents that are rational numbers. In particular, we’ll study quantities raised to the power of a fraction, also known as radical expressions.

Click below to go to the main reviewers:

Ultimate UPCAT Reviewer

Ultimate NMAT Reviewer

Ultimate PMA Entrance Exam Reviewer

Ultimate LET Reviewer

What Is a Radical?

A radical is an expression or quantity that has the radical symbol or uses a root (√).

The first time you probably encountered radicals was when you first learned about the square root of numbers. You know that the square root of a number is the number that, when multiplied by itself, will produce the original number. For instance, √25 = 5 since 5 x 5 = 25.

However, radicals are not just square roots. We also have cube roots. The cube root of the number is the number that, when multiplied by itself thrice (or three times), will produce the original number. For instance, ∛27 = 3 since 3 x 3 x 3 = 27.

We can extend the concept of square roots and cube roots to the fourth root (∜), fifth root, sixth root, and so on. 

Example: Evaluate the following roots:

1. √49
2. ∛125
3. √121

Solution:

• √49 is equal to 7 since 7 x 7 = 49;
• ∛125 is equal to 5 since 5 x 5 x 5 = 125; and
• √121 is equal to 11 since 11 x 11 = 121.

 

What Is a Radical Expression?

If we are talking about the root of a quantity that involves variables, we are now dealing with radical expressions. For example, √x is a radical expression since we have a variable under a radical sign.

Here are some examples of a radical expression:

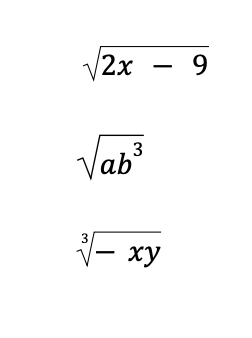
Can you provide your examples?

 

Parts of a Radical Expression

A radical expression has three parts or components: the radical symbol, the radicand, and the index or degree of the radical.

Let us take a look at ∛x

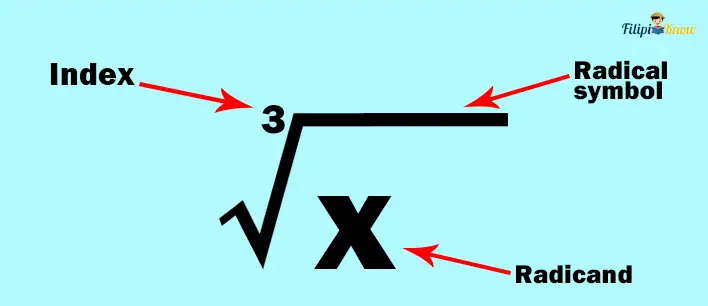
The radical symbol or radical sign is the symbol that indicates we are taking the root of a number. In this case, we are seeing the radical symbol with a 3 written on the left side. This means we are taking the cube root of the number inside the radical sign.

On the other hand, the radicand is the quantity inside the radical sign. It is the one that you are taking the root of. In ∛x, the radicand is x since it is the quantity inside the radical sign.

Lastly, we have the index or degree of the radical. This is the tiny number you can see on the upper left side of the radical sign. This number tells us how often to multiply the resulting number to obtain the radicand. For instance, in ∛x, the index or degree is 3.

The index also tells us what root we are taking. In the case of ∛x, we are taking the cube root since the index is 3. If the index is 4, it means we are taking the 4th root; if the index is 5, it means we are taking the 5th root, and so on. 

But what if the index is missing, like in the case of √16?

If the index is missing, it means the index equals 2. A missing index in the radical implies the square root of a number. Thus, the index or degree of the radical of √16 is 2.

Example: Determine the radicand and index of the following radical expressions:

Solution:

1. The radicand is x + 8, while the index is two since the index is missing in the radical symbol.
2. The radicand is a⁵ – 2, while the index is 2.
3. The radicand is 10, while the index is 4.
4. The radicand is y while the index is 3.
5. The radicand is 3 while the index is 2. Note that the two outside the radical sign is not part of the radicand.

 

Radicals As Quantities With Fractional Exponents

We can express radicals as quantities raised to fractional exponents.

Formally,

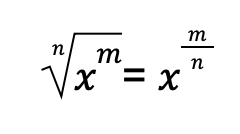
The equation above tells us that the index of the radical is the denominator of the fractional exponent of the radicand. Meanwhile, the power of the radicand is the numerator of the fractional exponent of the radicand.

For example, ∛y² means that 3 is the denominator of the fractional exponent of y while 2 is the numerator of the fractional exponent of y. Thus, ∛y² = y^2/3.

We can also state that if a number is raised to a fractional exponent, we can write it as a radical, with the denominator as the index of the radical and the numerator as the exponent of the radical.

For instance, j^1/2 means that 2 will be the index of the radical and 1 will be the exponent of the radicand (the quantity inside the radical sign).

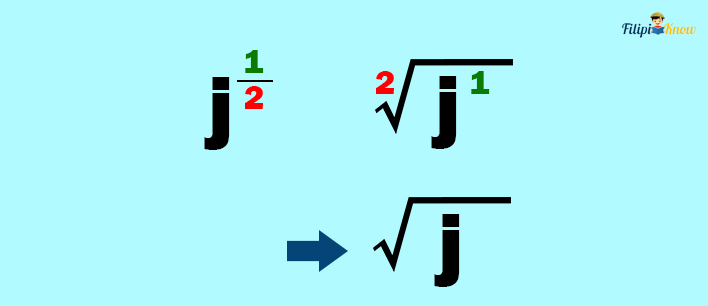
Since we don’t have to write 2 as an index, the answer is √j.

Example 1: Write √15 as an expression with fractional exponents.

Solution: The index of √15 is 2, and we have 1 as the power of the radicand. Therefore, our fractional exponent is ½. Thus, √15 = 15^1/2.

Example 4: Write a^3/4 as a radical expression. 

Solution: The denominator of the fractional exponent of a^3/4 is 4. This means that the index of our radical is 4. Meanwhile, the numerator of the fractional exponent is 3. Hence, it will be the power of our radicand. Therefore, a^3/4 is equal to ∜a³.

Example 5: Write (y – 1)^⅓ as a radical expression.

Solution: The denominator of the fractional exponent is 3. This means that the index of our radical is 3. Meanwhile, the numerator of the fractional exponent is 1. Hence 1 will be the power of our radicand. Therefore, (y – 1)^⅓ = ∛(y – 1).

When writing a radical expression into an expression with a fractional exponent, please take note that we can simplify the fractional exponent into its lowest terms. 

Suppose we want to write ∜b² as an expression with a fractional exponent. Using the technique we have used above, ∜b² = b^2/4

However, please note that we can reduce 2/4 into its lowest terms which is ½. Thus, b^2/4 is also equivalent to b^1/2.

Therefore, ∜b² = b^2/4  = b^1/2

 

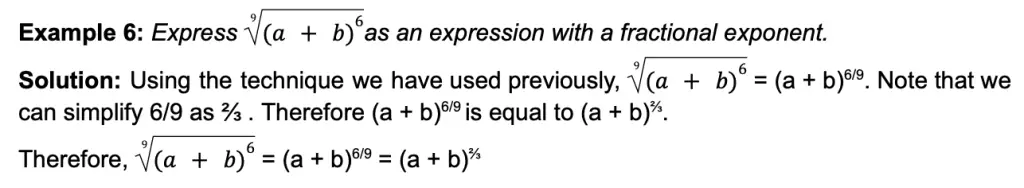
Properties of Radicals

In this section, we’ll discuss the mathematical properties of radicals. These properties are crucial in simplifying rational expressions and performing fundamental operations.

Property #1: If the radical index and the radicand’s power are equal, then the radical sign will cancel out, leaving us with only the radicand

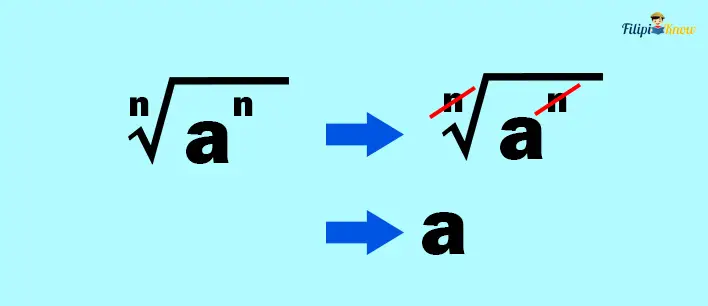
For instance, ∛a³ = a since the index of the radical and the power of the radicand are the same.

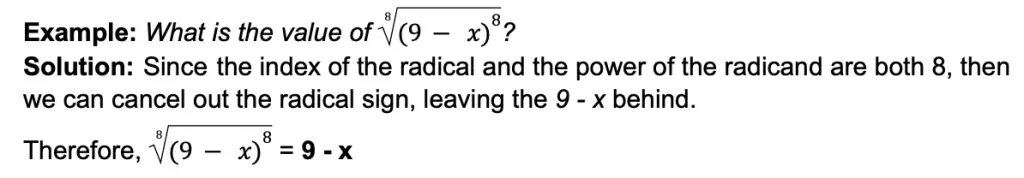
Property # 2: The root of the product of given numbers is equal to the product of the roots of the given numbers

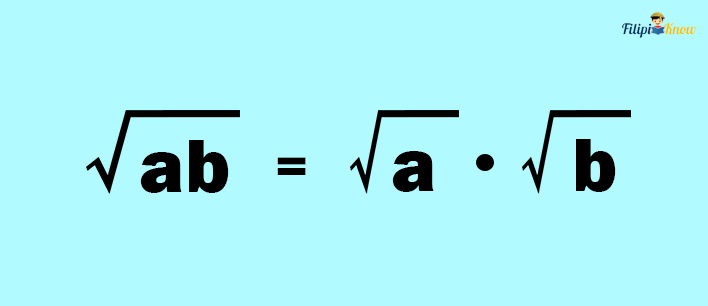
Consider √50. Notice that the numbers 10 and 5 will give a product of 50 when multiplied. Since the root of the product of two numbers is equal to that of the roots of these numbers, we can express √50 as a product of √10 and √5.

Hence,

√50 = √10 ✕ √5

The inverse of the second property is also true: the product of the roots of given numbers is equal to the root of the product of the given numbers.

For instance, if you try to multiply √8 and √11, you will obtain √88.

√8 ✕ √11 = √88

Property # 3: The root of the ratio of two numbers is equal to the ratio of the roots of two numbers

 

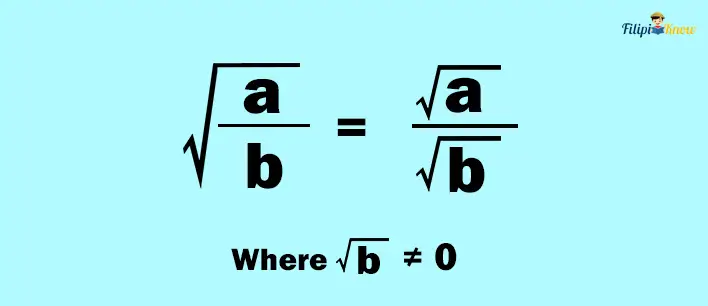
Simplifying Radical Expressions

Like any expression in mathematics, a given radical expression can also be written in its simplified form. Let us discuss how to simplify radical expressions in this section.

Radical Expressions in Simplified Form

How do we know if a given radical expression is in its simplest form?

A radical expression is in its simplified/simplest form if all of the following conditions are met:

• All exponents of its radicand have no common factor with the index of the radical 
• All exponents of its radicand are less than the index of the radical
• The radicand has no fractions involved
• There is no radical in the denominator
• In the case of the square root or cube root of a number: the radicand has no factor that is a perfect square number or a perfect cube number (we will discuss this later).

For example, √x is a radical expression in simplified form because:

• The exponent of its radicand (1) has no common factor with the index (2). 
• The exponent of its radicand (1) is less than the index (2).
• The radicand of √x has no fractions involved since the radicand is just x.
• There is no radical in the denominator of √x since the denominator of √x is simply 1.
• We are dealing with a square root; x is not a perfect square quantity.

Here’s another example:

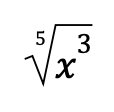
It is already in simplified form because:

• The exponent of its radicand (3) has no common factor with the index (5).
• The exponent of its radicand (3) is less than the index (5).
• The radicand has no fractions involved.
• No radical in the denominator.

Example: Determine which of the following radical expressions is/are in simplified form:

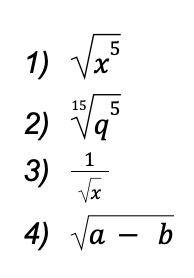
Solution:

1. The radical expression in item 1 is not in simplified form since the radicand’s power (5) is greater than the index of the radical (which is 2).
2. The radical expression in item 2 is not simplified since the radicand and the index have a common factor. The common factor of 5 (exponent of the radicand) and 15 (index) is 5.
3. The radical expression in item 3 is also not simplified since there’s a radical in the denominator.
4. The radical expression in item 4 is the only radical in simplified form. It satisfies the four conditions of the simplified form of a radical expression.

How To Simplify Radical Expressions

In this section, you will learn various techniques for simplifying radical expressions. We will be applying the properties of radicals, so make sure you already have a good grasp of them before proceeding.

Since most of the radicals we will be simplifying involve square roots and cube roots, you must have an idea about perfect square and cube numbers.

Perfect Square Numbers

Perfect square numbers are numbers whose square root is a whole number. For instance, 36 is a perfect square since √36 = 6. On the contrary, 21 is not a perfect square number since its square root is not a whole number (you can try inputting √21 in the calculator to verify).

Here’s a list of perfect square numbers from 1 to 100, which we advise you to remember:

Perfect Cube Numbers

Perfect cube numbers are numbers with a whole number cube root. For example, 8 is a perfect cube since ∛8 = 2. On the other hand, 9 is not a perfect cube number since its cube root is not a whole number (there’s no whole number that, when multiplied by itself thrice, will give 9). 

For your convenience, we have compiled the following list of perfect cube numbers from 1 – 100:

Using the concepts of perfect square and cube numbers and the properties of radicals, we can now simplify some radical expressions.

Example 1: Simplify √50

Solution: √50 is not yet simplified since 50 has a factor that is a perfect square number.

Since we are dealing with square roots, we can think of a factor of 50 that is a perfect square and express 50 as a product of that number and another number. 

Note that 25 is a perfect square number, and 25 x 2 = 50. Therefore, we can express √50 as

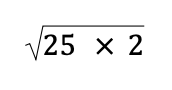
As per the second property of radicals (i.e., “the root of the product of given numbers is equal to the product of the roots of the given numbers”), we can express the answer above as √25 x √2.

We know that √25 = 5. Therefore, √25 x √2 = 5 x √2 or 5√2.

That’s it! We have simplified √50 into 5√2. Note that 5√2 has no perfect square factors anymore.

Example 2: Simplify the following:

Solution: The given radical is not in its simplest form since 27 still has a factor that is a perfect square (which is 9), and the exponent of its radicand (which is 3 in x³) is greater than the index (which is 2).

We know that 9 is a perfect square number and a factor of 27. Thus, we can express 27 as 9 ⋅ 3.

Meanwhile, we look for a factor of x³ that has the same power as the index. Our index is 2 so we look for a factor of x³ that has 2 as an exponent. In other words, we must factor x³ so that it has a factor with an exponent similar to the index (which is 2). x² is a factor of x³ since x² ⋅ x = x³.

This means that we can factor the given radicand as follows:

Applying the second property of radicals, we can express the root of a product as a product of the roots. 

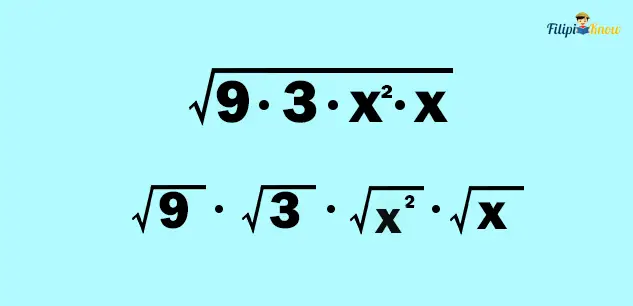
Finally, we can apply property #1, which states that if the index and the radical exponent have the same value, we can eliminate the radical sign and leave the radicand alone. Meanwhile, those radicals with radical signs that aren’t removed will be combined.

Therefore, the answer to our problem is 3x√3x.

Example 3: Simplify the radical expression below

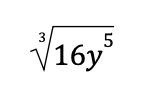
Solution: The given radical expression is not in simplified form since the number under the cube root sign has a factor that is a perfect cube, and the exponent of y⁵ is greater than the index.

To simplify this expression, we think of a factor of 16 that is a perfect cube and express 16 as a product of that factor and another number. 8 is a perfect cube number and 8 ⋅ 2 = 16. 

Meanwhile, we can factor y⁵ with a factor that has an exponent equal to the index (which is 3). In particular, y⁵ = y³ ⋅ y² 

Thus, we can express the given radical expression as follows:

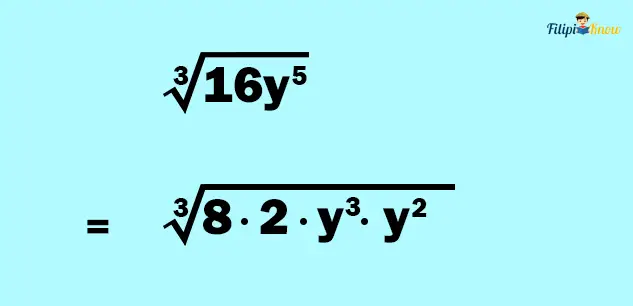
Using property #2 of radicals, we can express the root of a product as the product of the roots:

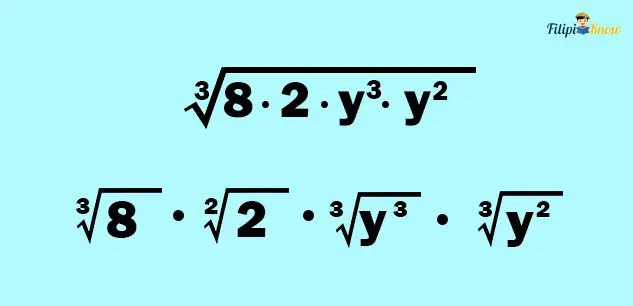
Lastly, using property # 1, we can cancel the radical sign of those expressions with the same index and power of the radicand to come up with the final answer.

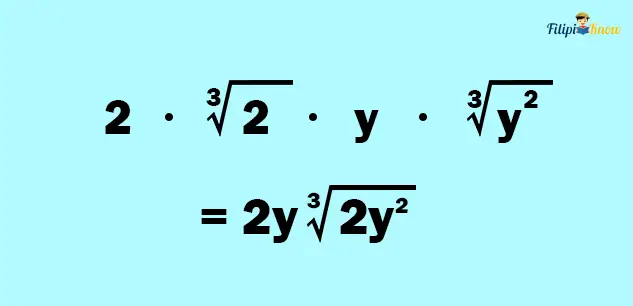
Example 4: Simplify the radical expression below

Solution: The given radical expression is not in simplified form since 128 has a factor that is a perfect square (which is 64), and the exponents of the radicand are greater than the index of the radical (which is 2).

Note that we can express 128 as 64 ⋅ 2.

On the other hand, we can express a³ as a product of two factors, one of which has an exponent equal to the index (which is 2). In particular, a²⋅ a. 

Meanwhile, b⁵ can also be expressed as a product of three factors, two of which have an exponent of 2. In particular, b⁵ = b² ⋅ b² ⋅ b

Therefore, we can express the given radical expression as:

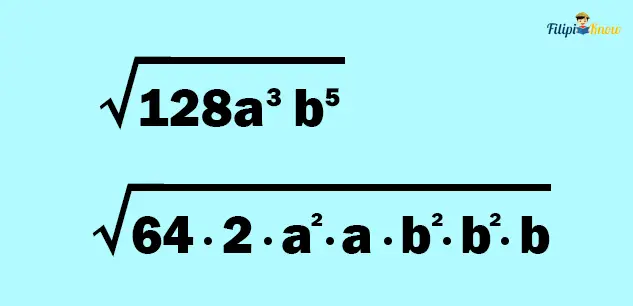
Following the second property of radicals:

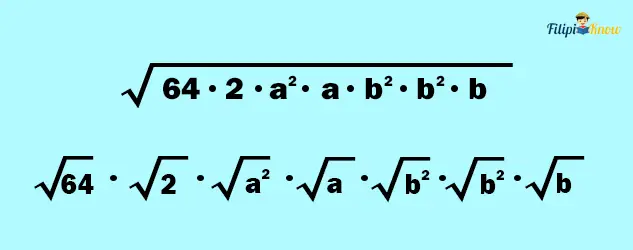
Lastly, as per the first property of radicals, we can remove the radical sign of those expressions with exponents equal to the index of the radical.

 

Rationalizing the Denominator of a Radical Expression

In the previous section, we discussed some techniques to simplify radical expressions.

However, we haven’t explored expressions with a radical sign in the denominator yet.  In this section, we will discuss rationalizing the denominator or removing the radical from the denominator of an expression.

What Does “Rationalize the Denominator” Mean?

In simple words, rationalizing the denominator of a radical expression means removing the radical from the denominator of an expression.

For instance, 1⁄√x can be simplified by rationalizing its denominator. This means we can write it using its equivalent expression without a radical in the denominator. After this process, the expression 1⁄√x will be √x⁄x(we will learn the steps later). Note that the resulting expression has no radical in the denominator.

How To Simplify Radical Expressions by Rationalizing the Denominator

To simplify radical expressions by rationalizing the denominator, follow these steps:

1. Multiply the numerator and the denominator by a certain radical that will remove the radical in the denominator.

Tip: If the radical in the denominator is a square root, then you can multiply the numerator and the denominator by a radical that will make the radicand a perfect square number. Suppose the radical in the denominator is a cube root. In that case, you can multiply the numerator and the denominator by a radical that will make the radicand a perfect cube number. 

2. Simplify the result, if possible.

Example 1: Simplify the following radical expression:

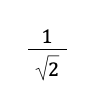
Solution: The given expression has a radical in the denominator, so we need to rationalize it.

1. Multiply the numerator and the denominator by a certain radical that will remove the radical in the denominator.

We aim to remove the radical in the denominator of the given expression ( √2). If we multiply it by √2, we will obtain √4 (a perfect square number), removing the radical sign.

Thus, we can multiply both the numerator and the denominator by √2:

2. Simplify the result, if possible.

The result we have obtained, which is √2⁄2, is already simplified. Therefore, the answer to our problem is √2⁄2.

Example 2: Simplify the radical expression below by rationalizing its denominator.

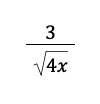
Solution:

1. Multiply the numerator and the denominator by a certain radical that will remove the radical in the denominator.

We aim to remove the radical in the denominator (√4x).

Note that we can simplify the denominator √4x into 2√x. So, we focus on removing the radical sign of √x in 2√x. If we multiply it by √x, we will obtain 2√x² = 2x, enabling us to remove the radical sign. 

Hence, we can multiply both the numerator and the denominator by √x:

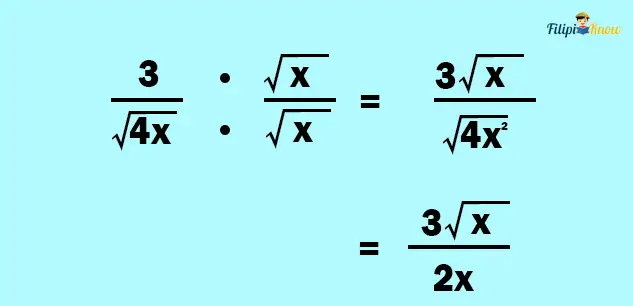
2. Simplify the result, if possible

The resulting expression we have obtained is 3√x⁄2x. This expression is already simplified, so we can skip this step. Hence, the answer to the given problem is 3√x⁄2x.

Example 3: Simplify the following radical expression:

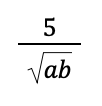
Solution: The denominator is √ab. Notice that we can remove the radical sign of √ab if we make it √a2b2 (having the same index and power of radicands removes the radical sign). Thus, we can multiply √ab by √ab so that the result will be √a²b² or simply ab.

Hence, we should multiply both the numerator and the denominator of the given radical expression by √ab: 

Example 4: Simplify the following radical expression:

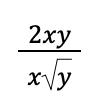
Solution: The denominator of the given radical expression is x√y. We can remove the radical sign of √y by making the radicand y a perfect square quantity. This means that we need to transform y into y².

This is possible by multiplying √y by √y. Since √y ⋅ √y  = √y² = y.

So, we multiply both the numerator and the denominator by √y:

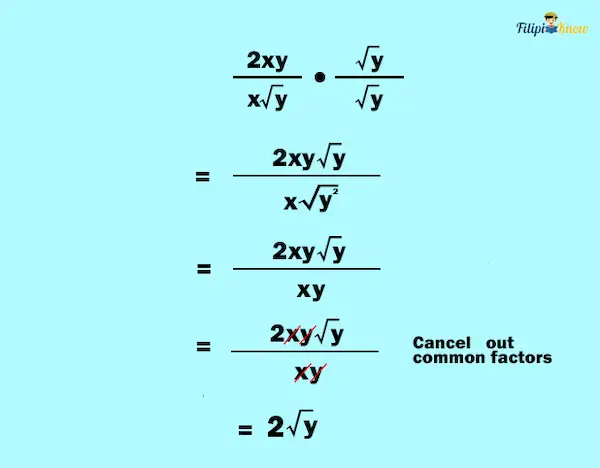
Hence, the answer is 2√y.

How To Rationalize the Denominator Using the Conjugate

Let’s say the denominator of a given expression consists of two terms, such as in

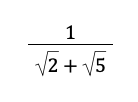
How do we rationalize this expression?

We simplify this kind of radical expression by multiplying the numerator and the denominator by the conjugate of the denominator. 

What is a conjugate?

A conjugate is an expression with the same terms as a given expression but with the opposite sign in the middle.

For instance, the conjugate of √2 + √5 is √2 – √5.

Example: Determine the conjugate of the following:

a) 1 – √3

b) √7 + √3

Solution:

a) 1 + √3

b) √7 – √3

Multiplying Conjugates

Before rationalizing the denominator using the conjugate, let us first review how to multiply conjugates.

Do you still remember the difference between two squares? It states that if we multiply expressions with two similar terms but have opposite signs (or the conjugates), we square the first term minus the square of the second term.

In other words,

(a + b)(a – b) = a² – b²

Thus, to multiply √2 + √5 by its conjugate, apply the difference between two squares:

Thus, the product of √2 + √5 and its conjugate, √2 – √5, is -3.

How To Rationalize the Denominator Using the Conjugate: 2 Steps

To rationalize the denominator using the conjugate, follow these steps:

1. Multiply the numerator and the denominator by the conjugate of the denominator.

2. Simplify the result, if possible.

Example 1: Simplify the following radical expression, which we used as an example above:

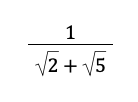
Solution:

1. Multiply the numerator and the denominator by the conjugate of the denominator

The conjugate of √2 + √5 is √2 – √5.

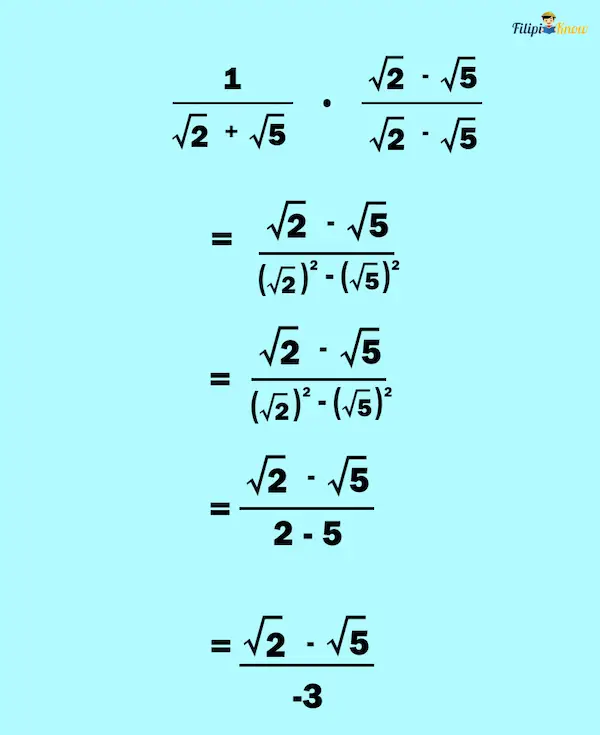
2. Simplify the result, if possible

The answer we have obtained is already in the simplest form, so it is our final answer.

Example 2: Simplify the radical expression below by rationalizing the denominator using the conjugate.

Solution:

 

Operations on Radicals

This section will discuss adding, subtracting, multiplying, and dividing radical expressions.

1. Addition and Subtraction of Radicals

Like and Unlike Radicals

Before we review how to add and subtract radicals, you must familiarize yourself with the concept of like and unlike radicals.

Two radicals are like radicals if they have the same index and radicand.

For example, √x and 5√x are like radicals because they have the same index (2) and radicand (x).

Another example: 9√b and -3√b are like radicals since they have the same index (2) and radicand (b).

On the other hand, unlike radicals have different indices or radicands. For example, 2√5 and 5√y are unlike radicals because their radicands are different even though they have the same index (which is 2).

√a and ∛a are also unlike radicals because even though they have the same radicand (a), they have different indices.

How To Add and Subtract Radical Expressions

Here are the steps to add and subtract radical expressions:

1. Simplify the given radical expressions. If the given radical expressions are already simplified, skip this step.

2. Add or subtract the coefficients of the like radicals in the resulting expressions from step 1. You cannot add or subtract unlike radicals.

Let us have some examples:

Example 1: Compute 3√a + 2√a – 4√a

Solution:

 1. Simplify the given radical expressions. If the given radical expressions are already simplified, skip this step.

All radical expressions in the given problem are in their simplest form; hence, we can skip this step. 

2. Add or subtract like radicals in the resulting expressions from step 1. You cannot add or subtract unlike radicals.

Since all the radicals are like radicals, we can add/subtract their coefficients and copy the common radical:

3√a + 2√a – 4√a

5√a – 4√a

√a

Hence, the answer is √a

Example 2: Add √20 and √5

Solution:

1. Simplify the given radical expressions. If the given radical expressions are already simplified, skip this step.

We can simplify √20 as 2√5. Thus, we have:

√20 and √5

2√5 + √5

2. Add or subtract like radicals in the resulting expressions from step 1. You cannot add or subtract unlike radicals.

Since 2√5 and √5 are like radicals, we can combine them:

2√5 + √5 = 3√5

Therefore, the answer is 3√5

Example 3:

Solution:

1. Simplify the given radical expressions. If the given radical expressions are already simplified, skip this step.

If we simplify each expression in the given, we have the following result (kindly review how to simplify radical expressions in the previous section):

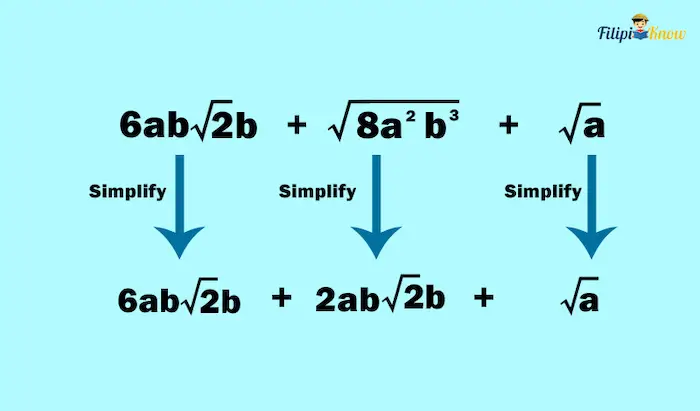
2. Add or subtract like radicals in the resulting expressions from step 1. You cannot add or subtract unlike radicals.

Based on what we have derived, we can only add radicals 6ab√2b and 2ab√2b; we cannot combine √a to them.

Thus, 

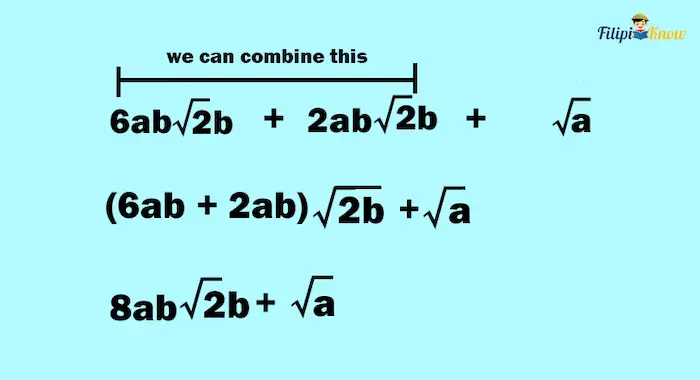
The answer is 8ab√2b + √a.

2. Multiplication of Radicals

There are two sets of guidelines to follow when multiplying radicals.

The first applies if the radicals have the same indices, while the second one should be followed when the given radicals have different indices.

a. Multiplying Radicals With the Same Indices

If the given radicals have the same index, multiply the radicals’ coefficients and radicands. Then, simplify the results, if possible.

Example 1: Multiply √2 by √4

Solution: Since both 2 and 4 have the same index (which is 2), then we can multiply the radicands (2 and 4) and the coefficients (both are 1).

√2 ⋅ √4 = √8

√8 is the product we have obtained. However, it is not yet simplified since it has a perfect square factor (4). So we need to simplify it:

√8 = √4 ⋅ √2 = 2√2

Hence, the final answer is 2√2

Example 2: Determine the product of 3√x and -2√xy

Solution: Since the given radicals have the same index (2), we can multiply the radicands and the coefficients.

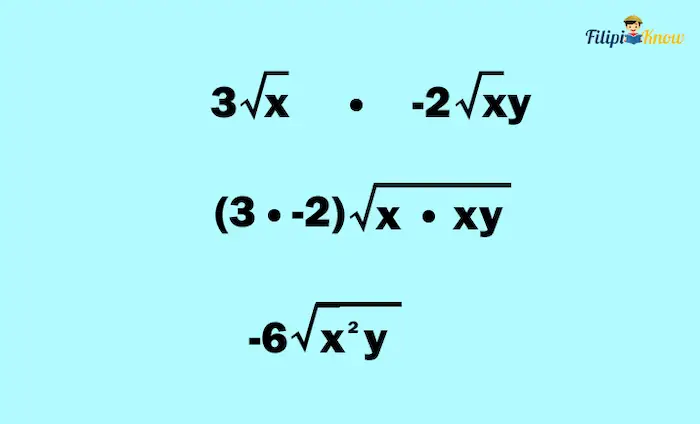
We can simplify the product further:

Thus, the final answer should be -6x√y

Example 3: Determine the product of the following:

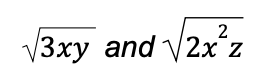
Solution: Since the given radicals have the same indices, we can multiply the radicands.

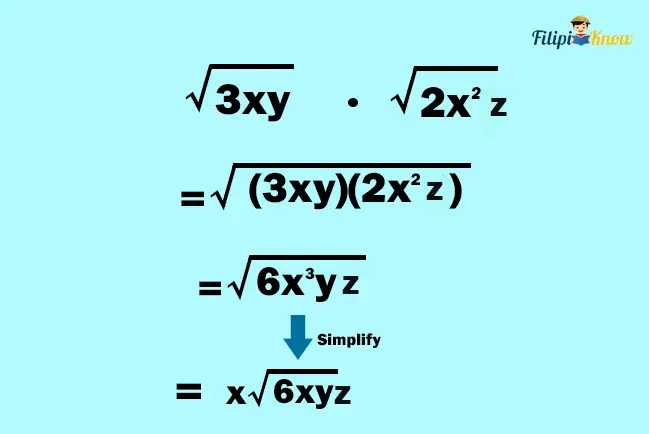
b. Multiplying Radicals With Different Indices

In this case, multiplying radicals is not that straightforward since you have to first make the index of the radicals similar before multiplying them.

How To Make the Index of Two Radicals Similar

1. Write the given radicals as expressions with fractional exponents. You will notice that the fractional exponents are dissimilar fractions.
2. Make the fractional exponents similar using their LCD. Write the expressions using similar fractional exponents.
3. Rewrite the expressions with similar fractional exponents in radical form.

Example 1: Make the indices of √3 and ∛2 similar.

Solution:

1. Write the given radicals as expressions with fractional exponents. You will notice that the fractional exponents are dissimilar fractions.

Recall that to transform a radical into an expression with a fractional exponent, we write the index as the denominator of the fractional exponent and the power of the radicand as the numerator (kindly review this concept in our previous section above).

This means that √3  = 3^1/2 and ∛2 = 2^1/3

Notice that the fractional exponents (½ and ⅓ ) are dissimilar.

2. Make the fractional exponents similar using their LCD. Write the expressions using similar fractional exponents.

If we make ½ and ⅓ similar, we will obtain 3/6 and 2/6.

Hence, we have 3^3/6 and 2^2/6

3. Rewrite the expressions with similar fractional exponents in radical form

That’s it! We’ve converted the given radicals with different indices into equivalent radicals with similar indices.

How To Multiply Radicals With Different Indices

To multiply radicals with different indices, make the indices similar first. Once you’ve converted them into radicals with the same index, follow the steps on multiplying radicals with similar indices.

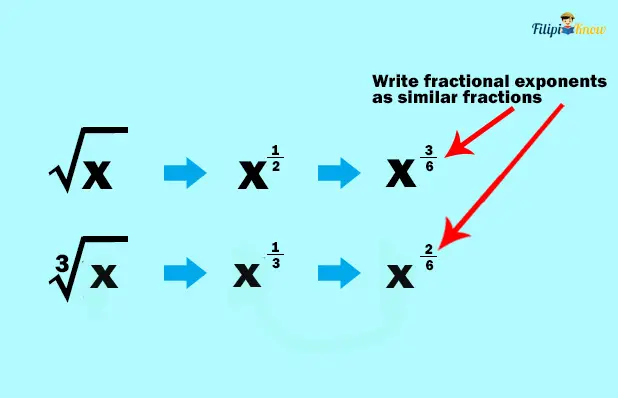
Example 1: Multiply √x by ∛x

Solution:

The given radicals have different indices, so we must first make them similar. Let us start by writing the given radicals into an expression with fractional exponents, then make the fractional exponents similar.

Converting the expressions with fractional exponents into radical form, we’ll obtain the following:

Since the radicals now have the same index, we can multiply the radicands:

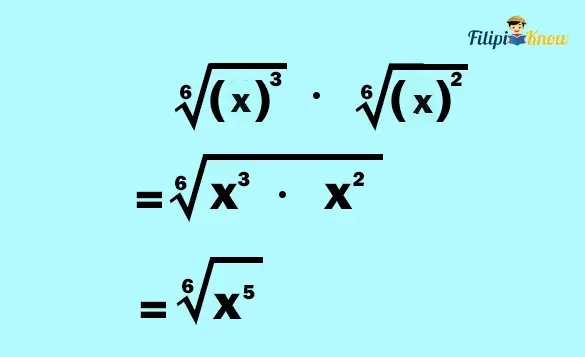
The answer can’t be simplified further, so it should be the final answer.

3. Division of Radicals

Do you still remember the third property of radicals that we discussed above? 

The property states that the root of the two quantities’ quotient is equal to that of the roots of these quantities. In symbols:

The reverse of this statement is also true. That is, the quotient of the roots of two quantities is equal to the root of the quotient of these quantities.

This property will guide us in dividing radicals.

Example 1: Divide √10 by √2

Solution: We can write the given problem as:

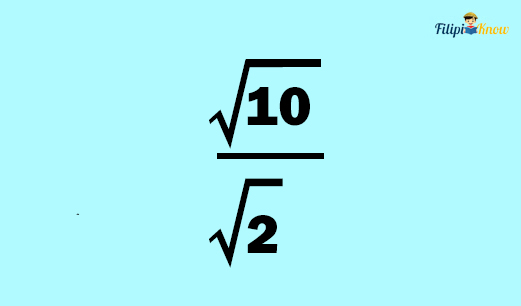
Invoking the third property of radicals allows us to write the problem as:

We can now divide the radicands:

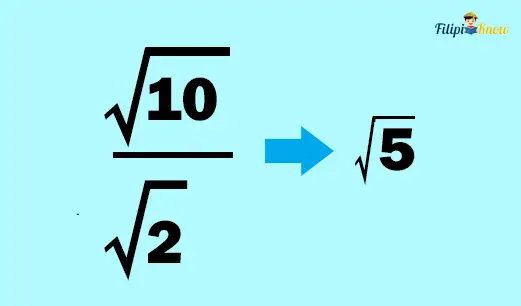
Hence, the answer is √5

Example 2: Divide √18 by √5

Solution:

We can write the given problem as:

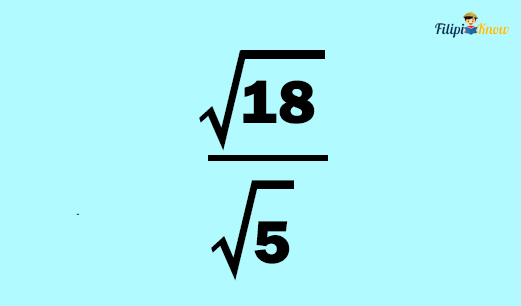
Note that using the third property this time is not advisable since 18 is not divisible by 5. Instead, we can simplify the expression by rationalizing the denominator.

To rationalize the denominator, we can multiply the numerator and the denominator by √5 so that the denominator will be √25, which is a perfect square number.

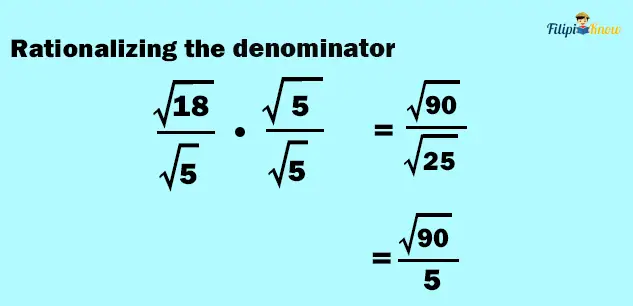
Simplifying the result:

 

Radical Equations

From the term itself, a radical equation refers to an equation that involves a radical sign. In this section, we will solve for the value of an unknown variable in a radical equation.

To solve a radical equation, follow these steps:

1. Isolate the terms that are under the radical sign from the terms that are not under the radical sign. This means that only one side of the equation must contain the terms under the radical sign.
2. Raise both sides of the equation by the power equivalent to the index of the radical to remove the radical sign.
3. Solve the resulting linear equation/quadratic equation.

Example 1: Solve for the value of x in the equation √x + 3 = 12

Solution:

1. Isolate the terms that are under the radical sign from the terms that are not under the radical sign. This means that only one side of the equation must contain the terms under the radical sign.

Looking at √x + 3 = 12, we must isolate x from the other quantity on the left-hand side. This can be achieved if we transpose 3 to the right-hand side of the equation.

√x + 3 = 12

√x  = -3 + 12

√x  = 9

2. Raise both sides of the equation by the power equivalent to the index of the radical to remove the radical sign.

The index of the radical in the equation is 2. Thus, we must raise both sides of the equation by 2 to remove the radical sign.

√x  = 9

(√x)² = (9)²

x = 81

3. Solve the resulting linear/quadratic equation.

The resulting equation is just x = 81, which tells us that the solution of the equation is 81.

Thus, the answer to the radical equation is x = 81.

Example 2: Solve for x in

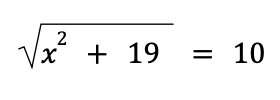
Solution:

1. Isolate the terms that are under the radical sign from the terms that are not under the radical sign. This means that only one side of the equation must contain the terms under the radical sign.

The terms under the radical sign in the given problem are already isolated. So, we can skip this step.

2. Raise both sides of the equation by the power equivalent to the index of the radical to remove the radical sign.

The index of the radical is 2, so we need to raise both sides of the equation by 2 to remove the radical sign.

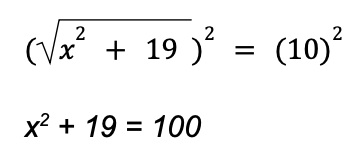
3. Solve the resulting linear/quadratic equation.

The resulting equation is x² + 19 = 100. This equation is quadratic.

Let us solve the equation:

x² + 19 = 100

x² = -19 + 100 Transposition method

x²  = 81

√x² = √81 Extracting the square root of both sides

x = ± 9

This means that the solutions of the radical equations are 9 and -9.

Radicals are one of the most interesting quantities in mathematics, but they are also quite hard to calculate algebraically because of their peculiar properties. It is advised that you read this reviewer repeatedly so you can further grasp the mathematical properties of radicals.

 

Next topic: Inequalities

Previous topic: Rational Expressions

Return to the main article: The Ultimate Basic Math Reviewer

 

Download Printable Summary/Review Notes

Download Printable Flashcards

Test Yourself!

1. Practice Questions [Free PDF Download]

2. Answer Key [Free PDF Download]

3. Math Mock Exam + Answer Key