In the previous chapter, we reviewed linear equations and how to use them to solve word problems. 

However, there are word problems where linear equations are insufficient to describe the given situation. In cases like these, we need another type of equation: the quadratic equation.

In this review, we’ll explore the definition of a quadratic equation, the different ways to solve it, and how we can apply it to solve word problems.

Click below to go to the main reviewers:

Ultimate UPCAT Reviewer

Ultimate PMA Entrance Exam Reviewer

Ultimate PNP Entrance Exam Reviewer

Ultimate LET Reviewer

What Are Quadratic Equations?

Quadratic equations are equations in the form ax² + bx + c = 0 where a, b, and c are real numbers and a is not equal to 0.

Simply put, a quadratic equation has two as the highest exponent of its variable. For example, x² + 4x + 4 = 0 is a quadratic equation since the highest exponent of the variable in this equation is 2.

Example: Which of the following are quadratic equations?

a) x² – 2x + 1 = 0

b) x² = 9

c) x + 2 = -2

Solution: The equations in letters a and b are quadratic since the highest exponent of their x (or variable) is 2. On the other hand, c is not a quadratic equation since the highest exponent of its x (or variable) is 1, making it a linear equation.

 

Standard Form of a Quadratic Equation

The standard form of a quadratic equation is ax² + bx + c = 0

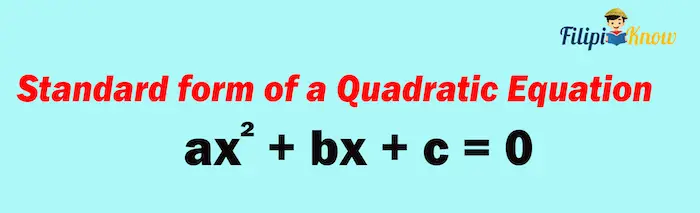
When we say that a quadratic equation is in standard form, it means that the terms of the equation are arranged in a manner where the exponents of the variable are decreasing.

For example, x² + 4x + 4 = 0 is in standard form because the terms are arranged in a manner where the exponents of the variable are in decreasing order.

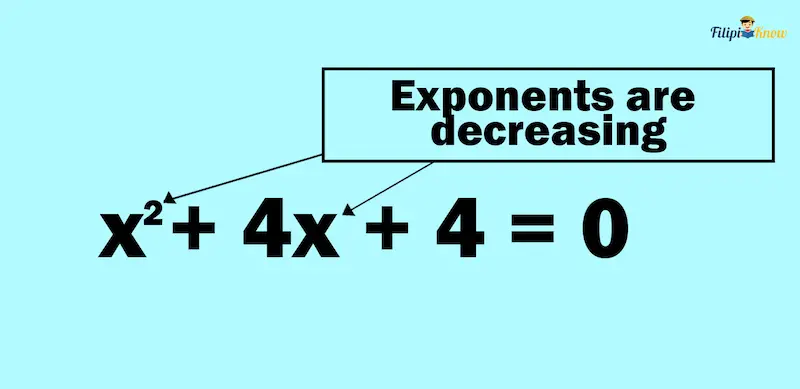
But why is it important to know if a quadratic equation is in standard form?

If a quadratic equation is in standard form ax2 + bx + c = 0, we can quickly determine the values for a, b, and c.

a, b, and c are the real number parts of the equation.

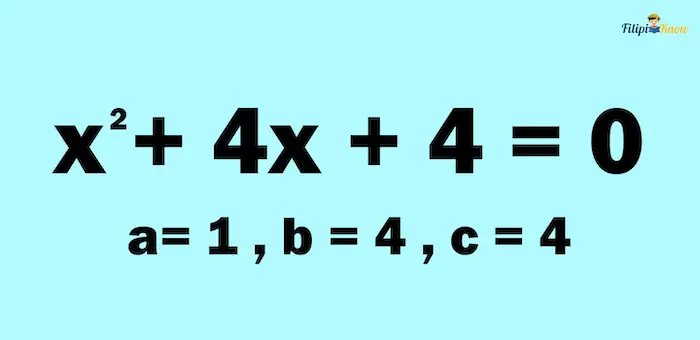
Retake a look at this equation: x² + 4x + 4 = 0. We already know that this quadratic equation is in standard form.

The a of a quadratic equation in standard form is the numerical coefficient of the quadratic term or the term with x². In x² + 4x + 4 = 0, the quadratic term is x² and its numerical coefficient is 1. Thus a = 1

The b of a quadratic equation in standard form is the numerical coefficient of the linear term or the term with x. In x² + 4x + 4 = 0, the linear term is 4x and its numerical coefficient is 4. Thus, b = 4.

Lastly, the c of a quadratic equation in standard form is the constant term or the term without the x. In x² + 4x + 4 = 0, the constant term is 4. Thus, c = 4.

Therefore, in x² + 4x + 4 = 0, the values of a, b, and c are a = 1, b = 4, and c = 4.

Example: Determine the values of a, b, and c (the real number parts) in 2x² + 4x – 1 = 0

Solution: Since the 2x² + 4x – 1 = 0 is already in standard form, then the values of a, b, and c are easy to determine:

• a = 2 (the numerical coefficient of 2x²)
• b = 4 (the numerical coefficient of 4x)
• c = -1 (the constant term is -1)

A quadratic equation’s a, b, and c can be determined only once we have expressed it in standard form ax² + bx + c = 0. Otherwise, we cannot immediately tell the values of a, b, and c.

Later in this review, you’ll learn the importance of determining the values of a, b, and c of a quadratic equation, especially when solving them using the quadratic formula.

 

Different Forms of Quadratic Equations

Not every quadratic equation you will encounter and solve is standard. Quadratic equations appear in different forms. It is essential to learn about them since there are specific techniques that we can use to solve equations in these forms.

ax² = c or ax² + c = 0 Form.

Quadratic equations such as x² = 9, 2x² = 16, 5x² = 10, -x² = -1 are in the form ax² = c. As you might have noticed, quadratic equations in this form do not have a linear term or a term with a variable raised to 1. 

Quadratic equations in the form ax² = c can also appear in the form of ax² + c = 0. 

For example, x² = 9 is a quadratic equation in ax² = c form. However, if we transpose 9 to the left-hand side of the equation, it will result in the following:

x² = 9

x² – 9 = 0 Transposition Method

This shows that x² = 9 is the same as x² – 9 =0. In other words, quadratic equations in ax² = c form can also appear in the form ax² + c = 0.

We usually extract the square root to solve quadratic equations in these forms. You will learn more about this method in the succeeding sections.

(x + a)(x + b) Form or the Factored Form.

In some quadratic equations, the exponent of 2 in the variable can’t be identified unless you perform some computations first.

For instance, (x + 2)(x + 3) = 0 can be considered a quadratic equation.

You’re probably asking: “But there’s no x² in (x + 2)(x + 3) = 0, so why is it a quadratic equation?”

Try to perform the FOIL method on (x + 2)(x + 3) and let’s see what we’ll obtain:

(x + 2)(x + 3) when multiplied is equal to x2 + 5x + 6. Thus, the equation (x + 2)(x + 3) = 0 is actually x2 + 5x + 6 = 0. This is why (x + 2)(x + 3) = 0 is a quadratic equation.

Here are more examples of a quadratic equation in (x + a)(x + b) form or factored form:

• (x + 1)(x – 3) = 0
• (x – 2)(x + 1) = 0
• (x – 1)(x – 1) = 0

Example: Which of the following are quadratic equations?

a) (x + 2)(x – 1) = 0

b) x² + x³ = -9

c) 2x² + 3x = -1

d) x² = 1

Solution:

• Equation a is a quadratic equation in factored form.
• Equation b is NOT a quadratic equation since the highest exponent of its variable is 3.
• Equation c is a quadratic equation but not yet in standard form. We can transpose -1 to the left side to be in standard form.
• Equation d is a quadratic equation in ax² = c form.

Thus, equations a, c, and d are all quadratic equations.

 

How To Solve Quadratic Equations

Let us discuss in this section the different methods of solving quadratic equations. 

Method 1: How To Solve Quadratic Equation by Extracting Square Roots

We usually use this method to solve for x of quadratic equations in the ax² = c or ax² + c = 0 form.

Here are the steps to solve quadratic equations by extracting the square root:

1. Isolate the square variable (x²) from other quantities. This means that x² must be the only quantity on the left side, and other quantities must be on the right side.
2. Take the square root of both sides of the equation.

Example 1: Solve for x in x² = 9

Solution:

Step 1: Isolate the square variable (x²) from other quantities.

x² is the only quantity on the left-hand side of x² = 9. This means that x² is already isolated from other quantities. Thus, we can skip this step.

Step 2: Take the square root of both sides of the equation.

We get the square root of both sides of the equation.

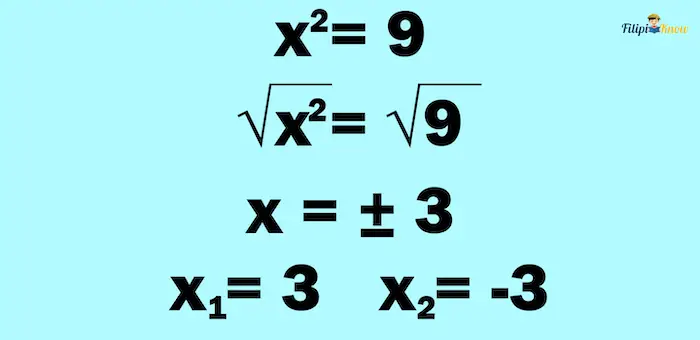
Notes:      

• If we get the square root of x², the result will be x.
• There are two square roots of a number: a positive root and a negative root; this is why we put the sign ± when we take the square root of a number.

Thus, the answers are x₁ = 3 and x₂ = -3

The solutions of a quadratic equation are also called the roots of a quadratic equation. Thus, when we say the roots of x² = 9, we refer to the solution of x² = 9.

Example 2: What are the roots of 2x² = 8?

Solution:

Step 1: Isolate the square variable (x²) from other quantities.

To remove the numerical coefficient and make x² the only quantity on the left-hand side of the equation, we can divide both sides by 2.

2x²⁄2 = 8⁄2

x²  =  4

Step 2: Take the square root of both sides of the equation.

x²  =  4

√x²  =  √4

x  = ±2

Thus, the roots of the equation are x₁ = 2 and x₂ = – 2

Example 3: What are the roots of x² + 4 = 20?

Solution:

Although the given equation seems to be not in the ax² = 0 or ax² + c = 0 form, we can manipulate the equation to solve it by extracting the square root.

Step 1: Isolate the square variable (x²) from other quantities.

To isolate x² from other quantities, we can transpose 4 to the right-hand side of the equation:

x² + 4 = 20

x² = – 4 + 20

x² = 16

Step 2: Take the square root of both sides of the equation.

x² = 16

√x² = √16

x  = ±4

Thus, the roots of the equation are x₁ = 4 and x₂ = – 4

Example 4: Solve for the roots of 2x² – 6 = 0

Solution:

Step 1: Isolate the square variable (x²) from other quantities.

To isolate x² from other quantities, we can transpose -6 to the right-hand side of the equation:

2x² – 6 = 0

2x² = 6

2x²⁄2 = 6⁄2

x² = 3

Step 2: Take the square root of both sides of the equation.

x² = 3

√x² = √3

x  = ± √3

√3 is not a perfect square number (there’s no integer multiplied by itself that will give 3). Thus, we write it as √3.

Thus, the roots of the equation are x₁ = √3 and x₂ = – √3

Example 5: Solve for x in x² – 19 = 6

Solution:

x² – 19 = 6

x² = 19 + 6 Transposition Method

x² = 25

√x² = √25    Taking the square root of both sides

x = ±5

The values of x are 5 and -5

Example 6: Solve for x in (x + 4)² = 9

Solution:

Note that it is much easier if we start extracting the square root of both sides first so that the resulting equation is just a linear equation:

(x + 4)² = 9

√(x + 4)² = √9 Taking the square root of both sides

x + 4 = ±3

Since we have two square roots for 9, we are going to have to solve two linear equations:

• Equation 1: x + 4 = 3
• Equation 2: x + 4 = -3

Solving for Equation 1 first:

x + 4 = 3

x = – 4 + 3 Transposition Method

x = – 1

Thus, the first root is -1

Solving for Equation 2:

x + 4 = – 3

x = – 4 + (-3)

x = – 7

Thus, the second root is -7

Therefore, the roots of the quadratic equation are – 1 and – 7.

 

Method 2: How To Solve Quadratic Equations by Factoring

In this method, we will apply what you have learned about factoring, precisely the method of factoring quadratic trinomials.

To solve quadratic equations by factoring, follow these steps:

1. Express the given equation in standard form. This means that one side of the quadratic equation must be 0.
2. Factor the expression. You must come up with two factors after factoring.
3. Equate each factor to zero and solve each resulting equation.

Example 1: Solve for the roots of x² + 5x + 4 = 0 by factoring.

Solution:

Step 1: Express the given equation in standard form. The given equation is already in standard form since it is in ax² + bx + c = 0 form, and one of the sides of the quadratic equation is already 0. Hence, we can skip this step.

Step 2: Factor the expression. To factor x² + 5x + 4, follow the steps on factoring quadratic trinomials.

 x² + 5x + 4 = 0

(x + 4)(x + 1) = 0

As shown above, we can come up with two factors x + 4 and x + 1.

Step 3: Equate each factor to zero and solve each resulting equation. We have obtained x + 4 and x + 1 as factors of x² + 5x + 4. We set both of these factors to zero. This means that we are going to have two linear equations.

• Equation 1: x + 4 = 0
• Equation 2: x + 1 = 0

Solving the equations above

Equation 1	Equation 2
x + 4 = 0	x + 1 = 0
x = – 4	x = – 1

Thus, the roots of the equation are x₁ = – 4 and x₂ = – 1.

Here’s a quick preview of what we have done above:

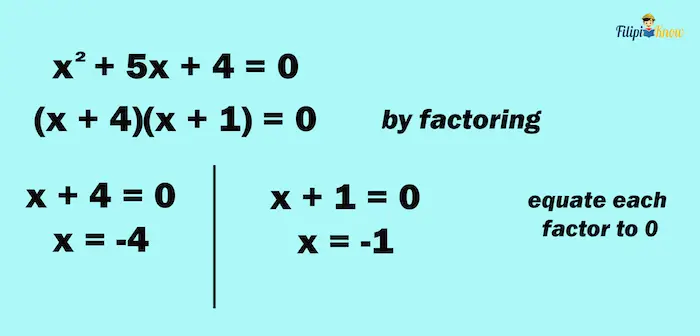
Example 2: Solve for the values of x in x² – 7x = – 10

Solution:

Step 1: Express the given equation in standard form. To express x² – 7x = – 10, we have to transpose – 10 to the left side so that the right side will be 0:

x² – 7x = – 10

x² – 7x + 10 = 0

Step 2: Factor the expression. Factoring x² – 7x + 10 will give us (x – 5)(x – 2)

x² – 7x + 10 = 0

(x – 5)(x – 2) = 0

Step 3: Equate each factor to zero and solve each resulting equation. We have obtained x – 5 and x – 2 as the factors of x² – 7x + 10. We set both of these factors to zero. This means that we are going to have two linear equations.

• Equation 1: x – 5 = 0
• Equation 2: x – 2 = 0

Solving the equations above

Equation 1	Equation 2
x – 5 = 0	x – 2 = 0
x = 5	x = 2

Thus, the roots of the equation are x₁ = 5 and x₂ =  2.

Here’s a quick review of our solution above:

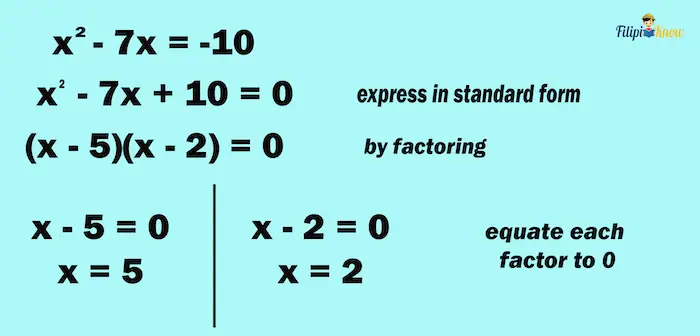
Example 3: Solve for the roots of 2x² + 3x – 2 = 0 by factoring.

Solution:

Step 1: Express the given equation in standard form. Since 2x² + 3x – 2 = 0 is already in ax² + bx + c = 0 form and one of its sides is already 0, we can skip this step.

Step 2: Factor the expression. You must come up with two factors after factoring. Factoring 2x² + 3x – 2 will give us (2x – 1)(x + 2):

2x² + 3x – 2 = 0

(2x – 1)(x + 2) = 0

Step 3: Equate each factor to zero and solve each resulting equation. We have obtained 2x – 1 and x + 2 as the factors of 2x² + 3x – 2. We set both of these factors to zero. This means that we are going to have two linear equations.

• Equation 1: 2x – 1 = 0
• Equation 2: x + 2 = 0

Solving the equations above

Equation 1	Equation 2
2x – 1 = 0	x + 2 = 0
2x = 1	x = – 2

To cancel the numerical coefficient in Equation 1, we divide both of its sides by 2:

2x⁄2 = ½

x = ½ 

Thus, the roots of the equation are x₁ = ½ and x₂ =  -2.

Here’s a quick review of what we have done above:

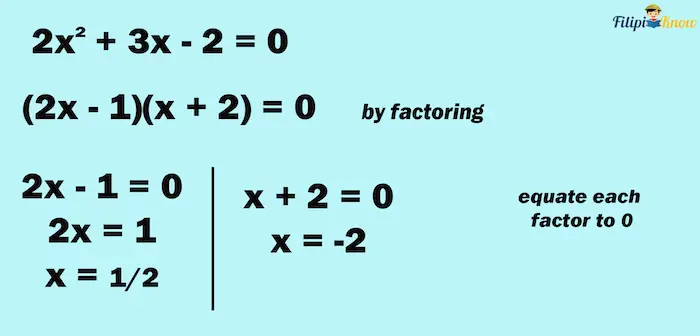
Factoring seems to be a powerful technique for solving quadratic equations. However, not every quadratic equation can be factored. For instance, x² + x + 2 = 0 cannot be solved by factoring since there are no two integers whose product is 2 and have a sum of 1. 

But don’t worry; there are other methods available that we can use in case a quadratic equation is not factorable. These methods are completing the square method and quadratic formula.

 

Method 3: How To Solve Quadratic Equations by Completing The Square

This method is advisable to use if a quadratic equation is non-factorable. 

To solve quadratic equations by completing the square, follow these steps:

1. Put the terms with variable x on the left-hand side of the equation while the constant term is on the right-hand side.
2. Divide both sides of the equation by a (or the coefficient of the quadratic term).
3. Divide the b (or the coefficient of the linear term) by 2 and square the result. Add the result to both sides of the equation.
4. Factor the left-hand side of the equation. Express the factors as a square of a binomial.
5. Take the square root of both sides of the equation.
6. Solve the resulting linear equations.

Don’t get intimidated by the steps above because we will discuss each in detail in our examples below.

Example 1: Solve for the roots of x² + 8x – 10 = 0

Solution:

A closer look will reveal that x² + 8x – 10 is non-factorable since there are no two integers whose product is – 10 and have a sum of 8. For this reason, we will solve x² + 8x – 10 = 0 by completing the square.

Step 1: Put the terms with variable x on the left-hand side of the equation while the constant term is on the right-hand side. In this case, transpose – 10 (i.e., the constant) to the right-hand side of the equation while all terms with x stay on the left-hand side.

x² + 8x – 10 = 0

x² + 8x = 10

Step 2: Divide both sides of the equation by a (or the coefficient of the quadratic term). The a in x² + 8x = 10 is the coefficient of x². The coefficient of x² is 1. If we divide x² + 8x = 10 by 1, the result will still be x² + 8x = 10.

Thus, we can skip this step.

Step 3: Divide the b (or the coefficient of the linear term) by 2 and square the result. Add the result to both sides of the equation. The b of x² + 8x = 10 is the coefficient of 8x which is 8. Thus, b = 8.

Divide 8 by 2 (8 ÷ 2 = 4)

Square the result (4² = 16)

The number we obtain is 16.

We add 16 to both sides of x² + 8x = 10:

x² + 8x = 10

x² + 8x + 16 = 10 + 16

x² + 8x + 16 = 26

We have obtained the equation x² + 8x + 16 = 26. After you apply this step, you will obtain a perfect square trinomial (i.e., x² + 8x + 16). As we have learned from a previous chapter, perfect square trinomials can be factored.

Step 4: Factor the left-hand side of the equation. Express the factors as a square of a binomial. The left-hand side of x² + 8x + 16 = 26  is x² + 8x + 16. This can be factored as (x + 4)(x + 4). We express (x + 4)(x + 4) as (x + 4)²

To summarize:

x² + 8x + 16 = 26

(x + 4)(x + 4) = 26

(x + 4)² = 26

Step 5: Take the square root of both sides of the equation.

Let us take the square root of both sides of the equation we have obtained from the previous step:

(x + 4)² = 26

√(x + 4)² = √26 Taking the square root of both sides

x + 4 = ±√26

Since 26 has two square roots (i.e., a positive and a negative square root), we have two linear equations:

• Equation 1: x + 4 = √26
• Equation 2:  x + 4 = -√26

Step 6: Solve the resulting linear equations.

Solving each linear equation:

Equation 1	Equation 2
x + 4 = √26	x + 4 = -√26
x = – 4 + √26	x = – 4  -√26

Therefore, the roots of the equation x² + 8x – 10 = 0  are x₁ = – 4 + √26   and x₂ = – 4  –√26

Here’s a quick review of what we have done above:

Example 2: Solve for the roots of 2x² + 12x + 14 = 0

Solution:

Since 2x² + 12x + 14 = 0 is not factorable, let us solve this quadratic equation by completing the square.

Step 1: Put the terms with variable x on the left-hand side of the equation while the constant term is on the right-hand side. By transposing 14 (i.e., the constant) to the right-hand side of the equation, all terms with x will remain on the left-hand side.

2x² + 12x + 14 = 0

2x² + 12x = – 14

Step 2: Divide both sides of the equation by a (or the coefficient of the quadratic term). The a in 2x² + 12x + 14 = 0  is the coefficient of x². The coefficient of 2x² is 2. Thus,

2x² + 12x = – 14

[2x² + 12x] ÷ 2 = -14 ÷ 2

x² + 6x = – 7

Step 3: Divide the b (or the coefficient of the linear term) by 2 and square the result. Add the result to both sides of the equation. The b of x² + 6x = – 7 is the coefficient of 6x which is 6. Thus, b = 6.

Divide 6 by 2 (6 ÷ 2 = 3)

Square the result (3² = 9)

The number we obtain is 9.

We add 9 to both sides of x² + 6x = -7:

x² + 6x = – 7

x² + 6x + 9 = – 7 + 9

x² + 6x + 9 = 2

We have obtained the equation x² + 6x + 9 = 2. After completing this step, you will obtain a perfect square trinomial. x² + 6x + 9 is a perfect square trinomial. As we learned from a previous chapter, perfect square trinomials can be factored.

Step 4: Factor the left-hand side of the equation. Express the factors as a square of a binomial. The left-hand side of the equation is x² + 6x + 9. This can be factored as (x + 3)(x + 3). We express (x + 3)(x + 3) as (x + 3)²

x² + 6x + 9= 2

(x + 3)(x + 3) = 2

(x + 3)² = 2 Expressing as a square of a binomial

Step 5: Take the square root of both sides of the equation.

Let us take the square root of both sides of the equation we have obtained from the previous step:

(x + 3)² = 2

√(x + 3)² = √2

x + 3 = ±√2

Since 2 have two square roots (i.e., a positive and a negative square root), we have two linear equations:

• Equation 1: x + 3 = √2
• Equation 2:  x + 3 = -√2

Step 6: Solve the resulting linear equations.

Solving each linear equation:

Equation 1	Equation 2
x + 3 = √2	x + 3 = -√2
x = – 3 + √2	x = – 3  -√2

Therefore, the roots of the equation 2x² + 12x + 14 = 0  are x₁ = -3  + √2   and x₂ = – 3  –√2

Here’s a quick review of what we have done above:

 

Method 4: How To Solve Quadratic Equations Using Quadratic Formula

The quadratic formula is a formula that will give you the roots of a quadratic equation. You can use this formula for any type or form of a quadratic equation.

The Quadratic Formula

The quadratic formula is:

Where:

• a is the numerical coefficient of the quadratic term
• b is the numerical coefficient of the linear term
• c is the constant term

The quadratic formula was derived by completing the square (see the previous method). If you are curious about how the quadratic formula was derived, kindly read the BONUS part of this review.

To use the quadratic formula, determine the values of a, b, and c first. Afterward, substitute these values to the formula and compute. You will arrive at two values because of the ± sign.

Example 1: Use the quadratic formula to solve for the values of x in 3x² – 2x – 1 = 0

Solution:

The values of a, b, and c are:

• a = 3
• b = – 2
• c = – 1

Let us substitute these values to the quadratic formula:

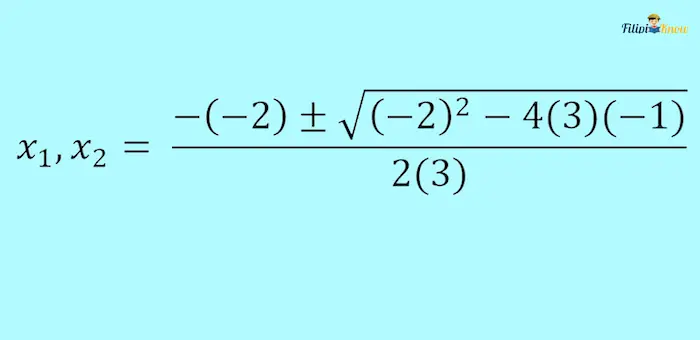
Computing for the values of x:

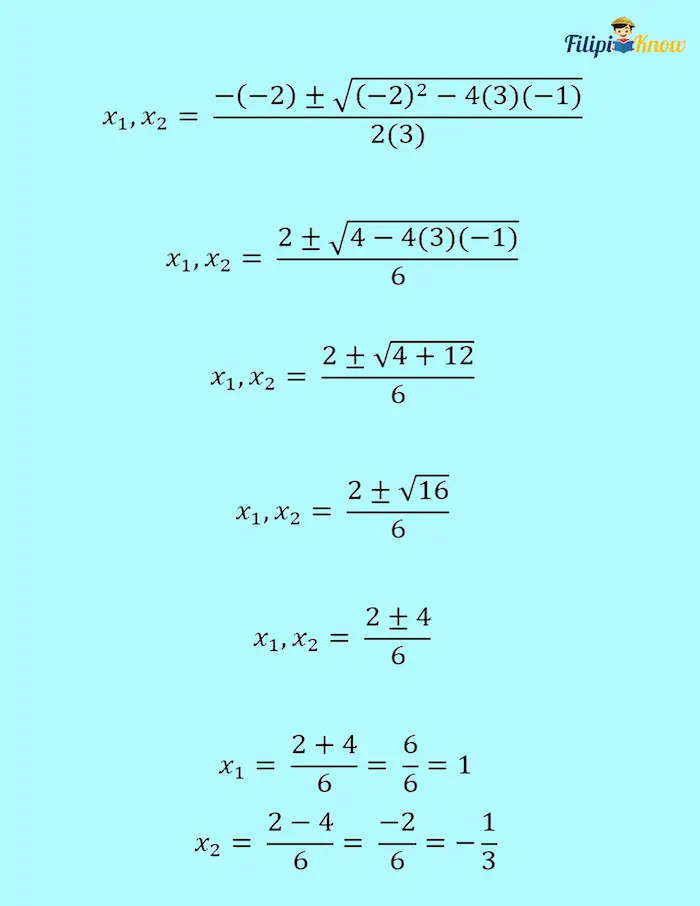
Hence, the roots of the equation are x₁ = 1 and x₂ = -⅓

Example 2: Use the quadratic formula to solve for the values of x in x² + 3x – 5 = 0

The values of a, b, and c are:

• a = 1
• b = 3
• c = – 5

Let us substitute these values to the quadratic formula:

Computing for the values of x:

 

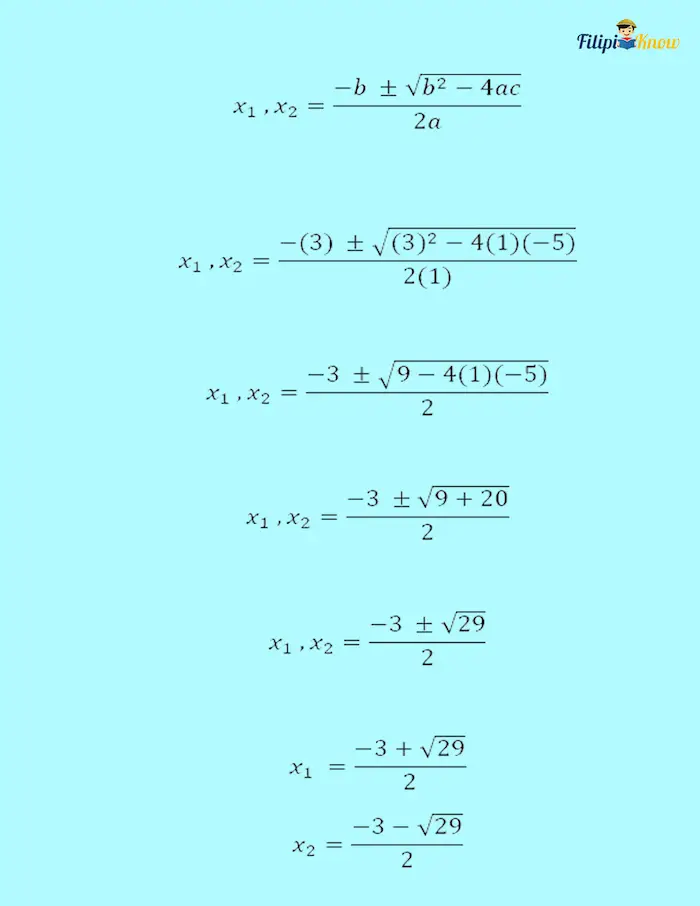
Discriminant of a Quadratic Equation

The discriminant of a quadratic equation allows you to determine the “nature of the roots” of a quadratic equation without actually solving it.

When we say “nature of the roots,” we are referring to three things:

1. The signs of the roots;
2. Whether the roots are real or complex numbers; and
3. Whether the roots are identical or not.

Through the discriminant, we can determine if a quadratic equation will give us roots that are real numbers or complex numbers, as well as if they are positive or negative numbers. We can also determine if that equation’s roots are identical.

The discriminant is the part of the quadratic formula under the radical sign (or the square root symbol).

What does the discriminant tell us?

• If the computed value of the discriminant is positive (D > 0), then the quadratic equation has two real distinct roots (or two real different roots).
• If the computed value of the discriminant is 0 (D = 0), then the quadratic equation has two identical real roots (or has only one repeated root).
• If the computed value of the discriminant is negative (D < 0), then the quadratic equation has no real roots. This means that the roots of the quadratic equation are complex numbers.

Let us have some examples:

Example 1: Using the discriminant, determine the nature of the roots of x² + 4x + 4 = 0

Solution:

We have a = 1, b = 4, and c = 4

Using the discriminant:

D = b² – 4ac

D = (4)² – 4(1)(4)

D = 16 – 16

D = 0

The value of the discriminant is 0. This means that the x² + 4x + 4 = 0 roots are identical (or one root is just being repeated).

If we try to solve x² + 4x + 4 = 0 using factoring:

x^2.+ 4x + 4 = 0

(x + 2)(x + 2) = 0

x₁ = – 2    x₂ = – 2

The roots of x² + 4x + 4 = 0 are both – 2. Indeed, the roots of the equation are identical and real numbers. The discriminant is correct.

Example 2: What is the nature of the roots of 2x² + 5x – 1 = 0?

Solution:

We have a = 2, b = 5, and c = – 1

Using the discriminant:

D = b² – 4ac

D = (5)² – 4(2)(-1)

D = 25 + 8

D = 33

The discriminant is positive. This means that the nature of the 2x² + 5x – 1 = 0 roots is real and distinct.

Try to verify using any method that 2x² + 5x – 1 = 0 roots are distinct and real.

Example 3: The quadratic equation x² – (k + 2)x + 49 = 0 has two identical roots. What must be the value of k?

Solution:

If the quadratic equation has two identical roots, its discriminant is equal to 0.

Thus, we set the following:

D = b² – 4ac

0 = b² – 4ac

We have a = 1, b = k + 2, and c = 49. Substituting these values:

0 = b² – 4ac

0 = (k + 2)² – 4(1)(49)

Now, let us solve for the value of k:

0 = k² + 4k + 4 – 196

0 = k² + 4k – 192

k² + 4k – 192 = 0

(k + 16)(k – 12) = 0

Equation 1	Equation 2
k + 16 = 0	k – 12 = 0
k = -16	k = 12

Therefore, the values of k should be k₁ = – 16 and k₂ = 12

 

Sum and Product of the Roots of a Quadratic Equation

There’s another fun thing about quadratic equations. We can determine their roots’ sum and product without actually computing for them. All you have to do is to use the formulas below.

The formula for the sum of the roots of a quadratic equation is:

x₁ + x₂ = -b⁄a

The formula for the product of the roots of a quadratic equation is:

x₁ ⋅ x₂ = c⁄a

The formulas above were derived using the quadratic formula, but this review will not show the derivation. You may refer here if you’re interested in the formulas’ derivation.

Example 1: What is the sum and product of the roots of x² + 8x + 2 = 0?

Solution:

Using the formulas for the sum and product of the roots:

Thus, the sum and product of the roots are – 8 and 2, respectively.

 

Using Quadratic Equations to Solve Word Problems

A lot of word problems can be described using quadratic equations. In this section, we will solve some word problems using quadratic equations.

Here are the steps that you may follow to solve word problems involving quadratic equations:

1. Read and understand the problem. Identify what is being asked.
2. Represent unknown quantities using a variable.
3. Construct a quadratic equation that represents the given situation or problem.
4. Solve the quadratic equation.

Example 1: The sum of two numbers is 8, while their product is 15. What are the numbers?

Solution:

Step 1: Read and understand the problem. Identify what is being asked. The problem asks us to determine two numbers whose sum is 8 and whose product is 15.

Step 2: Represent unknown quantities using a variable. Let x be one of the numbers. Since the sum of the numbers is 8, we can represent the second number as 8 – x.

• x = first number
• 8 – x = second number

Step 3: Construct a quadratic equation representing the given situation or problem. The problem states that the product of the numbers is 15. We can express it as:

(first number)(second number) = 15

Using the variables we set in Step 2:

x (8 – x) = 15

By the distributive property, we have:

8x – x² = 15

The equation above can be expressed in standard form as:

-x² + 8x = 15

Multiplying both sides by – 1, we obtain:

x² – 8x = – 15

x² – 8x + 15 = 0

Step 4: Solve the quadratic equation.

Let us solve for the values of x in x² – 8x + 15 = 0.  We can solve this quadratic equation by factoring:

x² – 8x + 15 = 0

(x – 3)(x – 5) = 0

x₁ = 3 x₂ = 5

Based on the solution of our quadratic equation, the numbers are 3 and 5.

Example 2: A small rectangular garden has a perimeter of 12 meters and an area of 8 square meters. Determine the length and width of the rectangular garden.

Solution:

Step 1: Read and understand the problem. Identify what is being asked. The problem asks us to determine the length and the width of the small rectangular garden given that its perimeter is 12 meters and its area is 8 square meters.

Step 2: Represent unknown quantities using a variable. Let l be the length of the small rectangular garden while let w represent its width.

Step 3: Construct a quadratic equation representing the given situation or problem. The perimeter of a rectangle is defined as P = 2l + 2w. Since the small rectangular garden has a perimeter of 12 meters, we have:

12 = 2l + 2w (Equation 1)

Meanwhile, the area of a rectangle is defined as A = l ⋅ w. Since the small rectangular garden has an area of 8 square meters, we have the following:

8 = l ⋅ w (Equation 2)

Using Equation 1, we can solve for the value of w in terms of l:

12 = 2l + 2w

12 = 2(l + w) Distributive Property

6 = l + w Division Property of Equality

w = 6 – l Transposition Method

Now, we substitute the value of w in terms of l in our second equation:

8 = l ⋅ w

8 = l (6 – l) Substituting w = 6 – l

8 = 6l – l²

We have obtained the quadratic equation 8 = 6l – l²

Note that we can write it in standard form:

8 = 6l – l²

l² – 6l + 8 = 0 Transposition Method

Step 4: Solve the quadratic equation.

Let us solve for l in l² – 6l + 8 = 0 by factoring:

l² – 6l + 8 = 0

(l – 4)(l – 2) = 0 

l₁ = 4 l₂ = 2

Thus, according to our solution, we have two values for the length of the small rectangular garden, which are 4 meters and 2 meters.

Let us substitute this value of l to w = 6 – l to determine the possible values of the width:

Using l₁ = 4:

w = 6 – 4

w₁ = 2

Using l₂ = 2

w = 6 – 2

w₂ = 4

Thus, the possible width values are 2 meters and 4 meters.

Hence the values of the length and width of the rectangle are 4 meters and 2 meters, respectively.

 

BONUS: How Was the Quadratic Formula Derived?

The quadratic formula was derived using the completing the square method:

 

Next topic: Rational Expressions

Previous topic: Linear Equations

Return to the main article: The Ultimate Basic Math Reviewer

 

Download Printable Summary/Review Notes

Download Printable Flashcards

Test Yourself!

1. Practice Questions [Free PDF Download]

2. Answer Key [Free PDF Download]

3. Math Mock Exam + Answer Key