We know that a fraction is a rational number that consists of integers as its numerator and denominator. But what if instead of integers, we replace them with polynomials?

Let me introduce you to the concept of rational expressions – the ratio of two polynomials. In this reviewer, we are going to review its definition and mathematical operations.

Click below to go to the main reviewers:

Ultimate UPCAT Reviewer

Ultimate NMAT Reviewer

Ultimate PMA Entrance Exam Reviewer

Ultimate PNP Entrance Exam Reviewer

Ultimate LET Reviewer

What Is a Rational Expression?

A rational expression (or rational algebraic expression) is a ratio of two polynomials. Think of it as a fraction but instead of whole numbers, its numerator and denominator are polynomials.

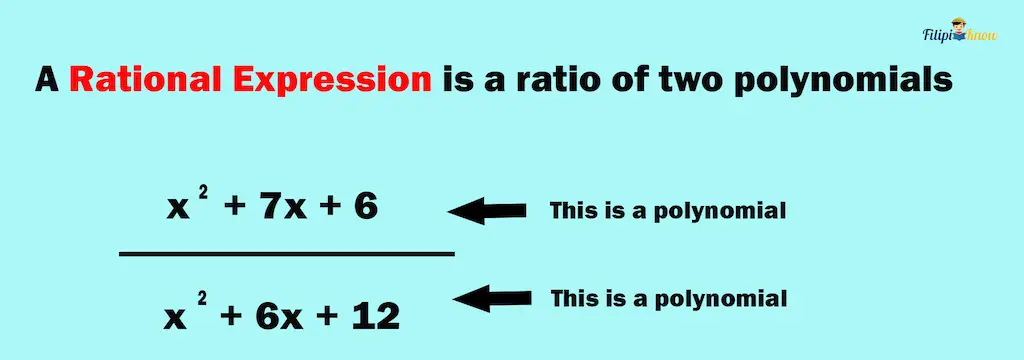
Formally, a rational expression R(x) is the ratio of two polynomials P(x) and Q(x), such that the value of the polynomial Q(x) is not equal to 0 (because division by 0 is undefined).

R(x) = P(x)∕Q(x), where Q(x) ≠ 0

Example: Which of the following is/are rational expressions?

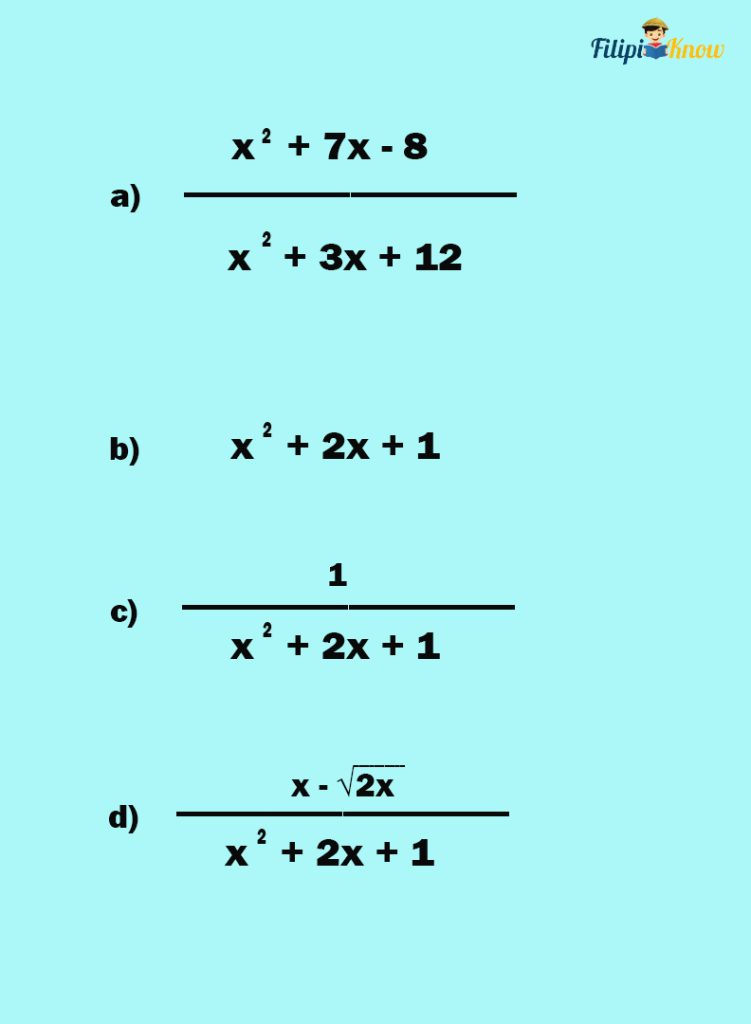
Solution:

The expression in a) is a rational expression since both its numerator and denominator are polynomials.

The expression in b) is also a rational expression because x² + 2x + 1 can be expressed as:

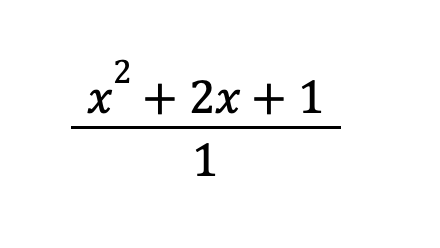
Take note that a constant can be considered a polynomial. Thus, b) has a numerator and denominator that are both polynomials.

The expression in c) is also a rational expression since its numerator (which is 1) is a polynomial while its denominator is also a polynomial.

The expression in d) is not a rational expression since its numerator is not a polynomial. Recall that if a variable is under the radical sign, then the expression is not a polynomial.

Simplifying Rational Expressions

Just like fractions, we can also reduce rational expressions into their simplest form. A rational expression is said to be in its simplest form if and only if its numerator and denominator have no common factor except 1.

For instance, let us take a look at the following rational expression:

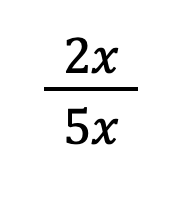
If we factor both the numerator and denominator, you will notice that there’s a common factor between them. That common factor is x:

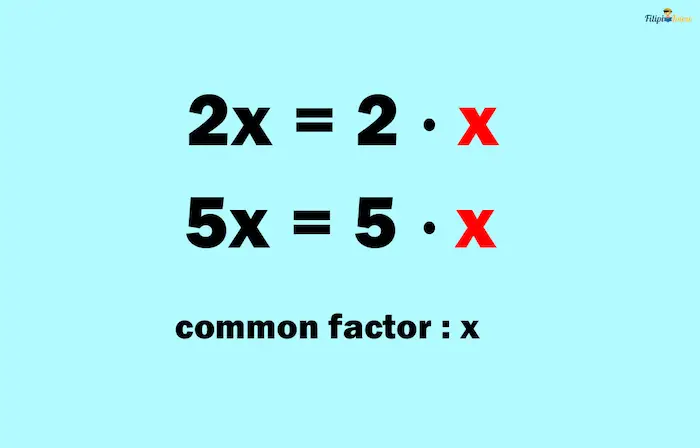
We can cancel out the common factor:

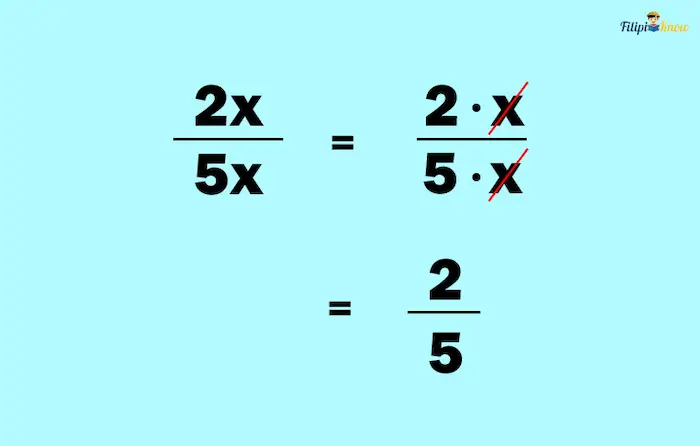
What’s left with us is ⅖. Both 2 and 5 are prime and have no common factor except 1. Therefore, the simplified form of the rational expression in this example is ⅖.

How To Simplify Rational Expressions: 3 Steps

Here are the steps to simplify a rational expression:

1. Factor the numerator and the denominator.
2. Look for the common factors between the numerator and the denominator.
3. Cancel out the common factors between the numerator and the denominator.

Example 1: Simplify the following rational expression:

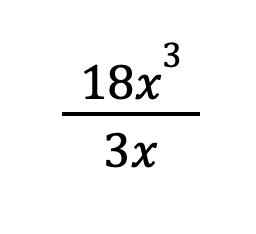
Solution:

1. Factor the numerator and the denominator.

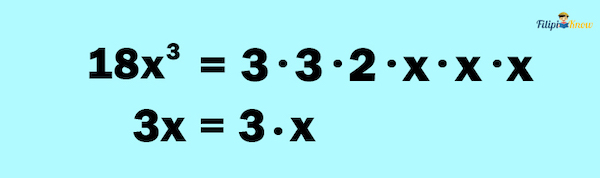
2. Look for the common factors between the numerator and the denominator.

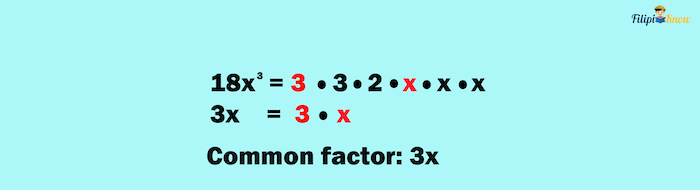
3. Cancel out the common factors between the numerator and the denominator.

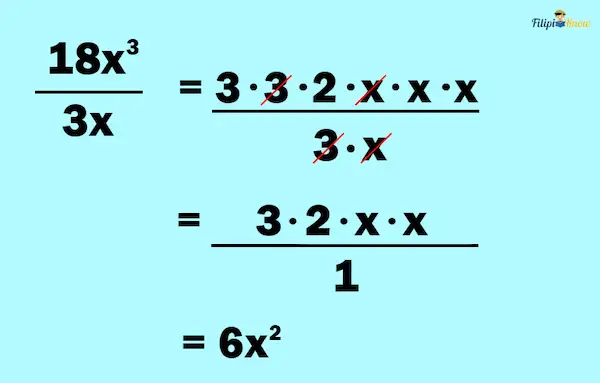
Thus, the simplified form of the rational expression is 6x².

Example 2: Simplify the following rational expression:

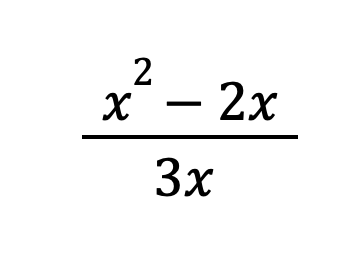
Solution:

1. Factor the numerator and the denominator

We can factor out x² – 2x as x(x – 2) by factoring using the Greatest Common Factor (GCF).

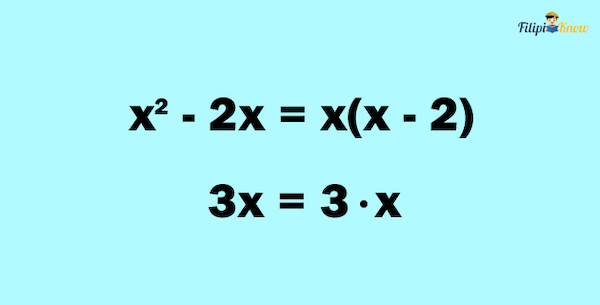
2. Look for the common factors between the numerator and the denominator

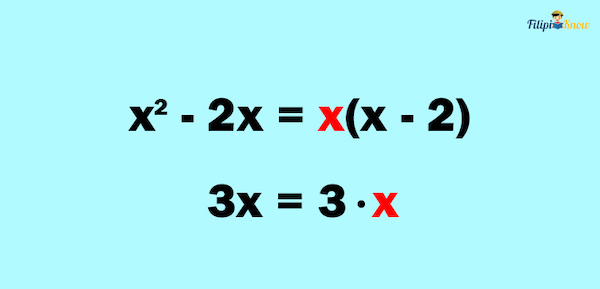
3. Cancel out the common factors between the numerator and the denominator

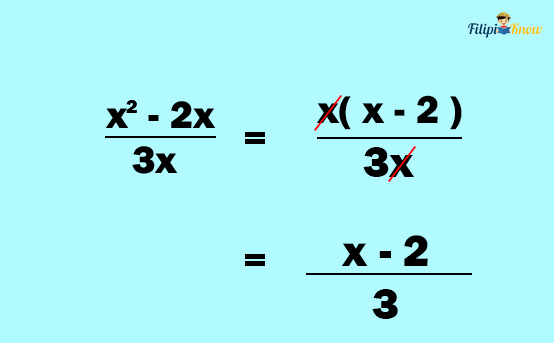
Example 3: Simplify the following rational expression:

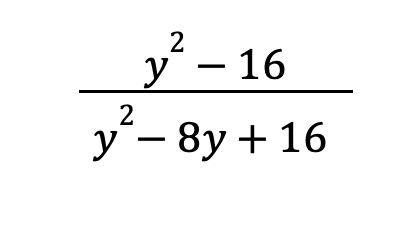
Solution:

1. Factor the numerator and the denominator

Since y² – 16 is a difference of the two squares, we can factor it as (y + 4)(y – 4). On the other hand, y² – 8y + 16 is a perfect square trinomial that we can factor as (y – 4)(y – 4).

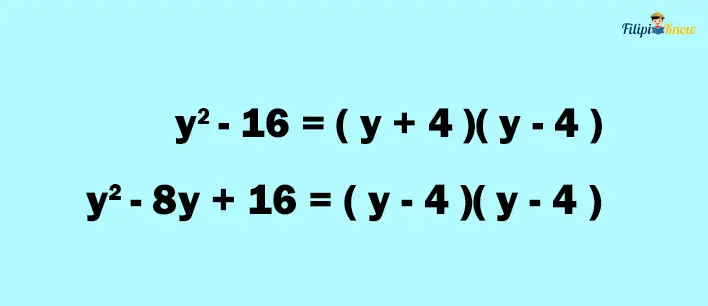
2. Look for the common factors between the numerator and the denominator

3. Cancel out the common factors between the numerator and the denominator

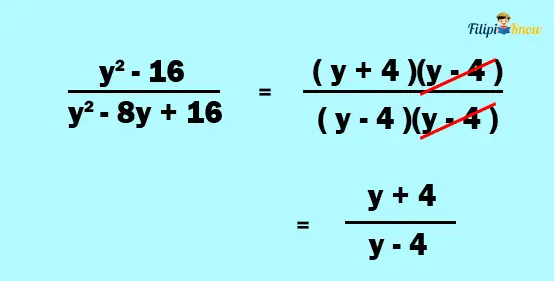
Example 4: Simplify the following rational expression:

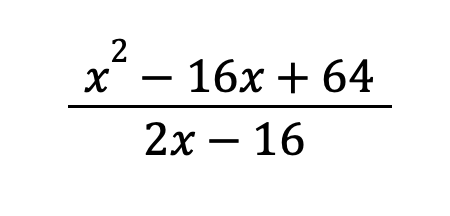
Solution:

1. Factor the numerator and the denominator

Since x² – 16x + 64 is a perfect square trinomial, we can factor it as (x – 8)(x – 8). Meanwhile, we can factor 2x – 16 as 2(x – 8) using its GCF.

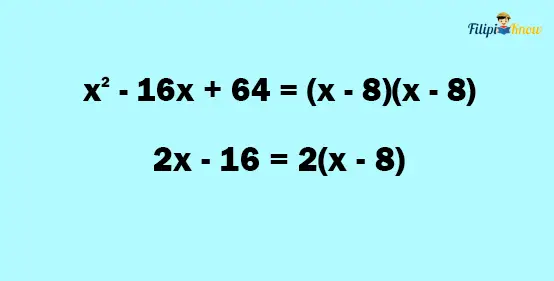
2. Look for the common factors between the numerator and the denominator

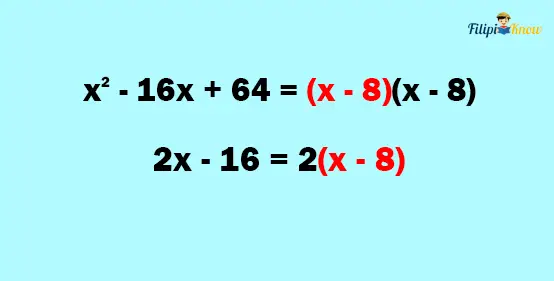
3. Cancel out the common factors between the numerator and the denominator

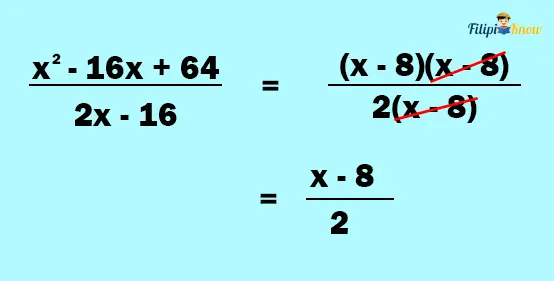
Example 5: Simplify the following rational expression:

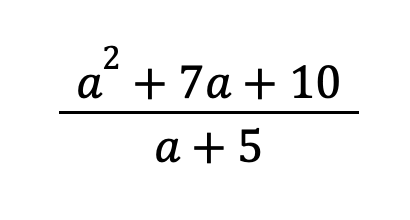
Solution:

1. Factor the numerator and the denominator

We can factor a² + 7a + 10 as (a + 5)(a + 2).

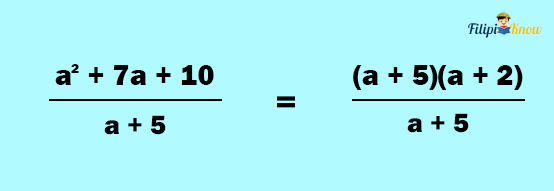
2. Look for the common factors between the numerator and the denominator

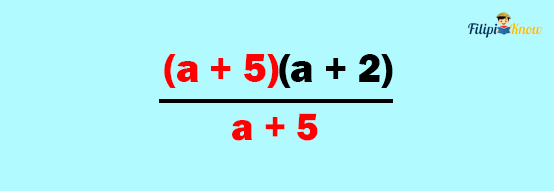
3. Cancel out the common factors between the numerator and the denominator

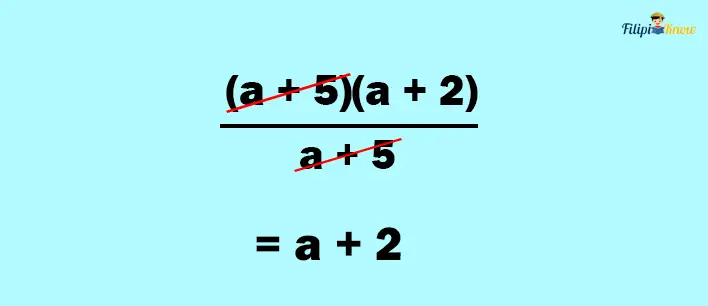
Therefore, the simplified form of the rational expression is a + 2.

Example 6: Simplify the following rational expression:

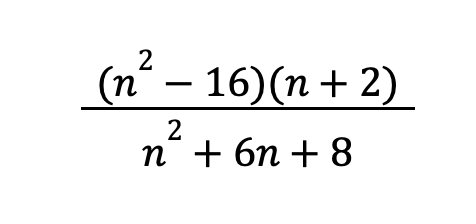
Solution:

1. Factor the numerator and the denominator

We can factor n² – 16 as (n + 4)(n – 4). Meanwhile, we can factor n² + 6n + 8 as (n + 4)(n + 2).

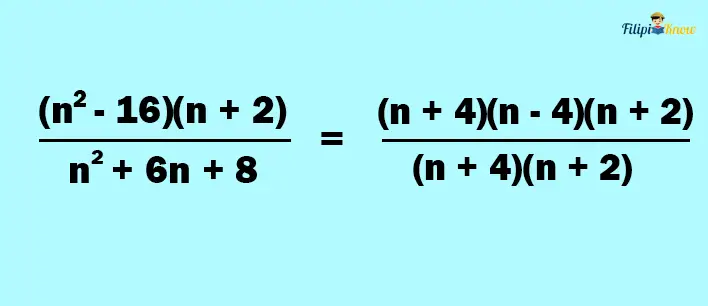
2. Look for the common factors between the numerator and the denominator

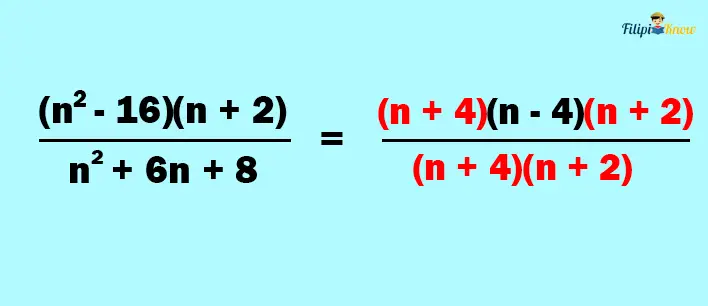
3. Cancel out the common factors between the numerator and the denominator

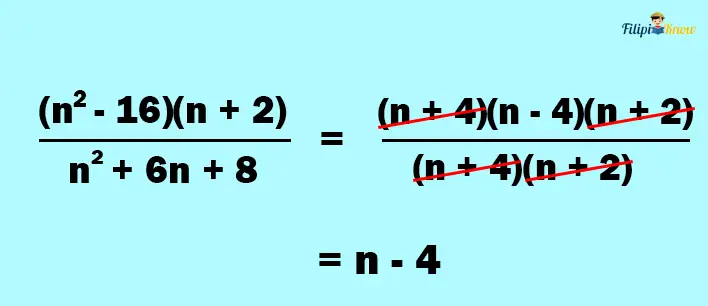
Thus, the answer to this example is n – 4.

How To Find the Least Common Denominator (LCD) of Rational Expressions

Before we study how to apply basic operations to rational expressions, you must learn first how to find the Least Common Denominator (LCD) of rational expressions.

To find the LCD of rational expressions, follow these steps:

1. Factor the denominators of the rational expressions.
2. Write the factors of the denominators. Match the common factors in columns.
3. Bring down each factor in every column. Common factors in the column must be brought down also.
4. Multiply the factors you brought down. The resulting expression is the LCD.

Example 1:

Solution:

The denominators of the given expressions are x – 1 and x² – 1. Our task is to determine their Least Common Denominator using the steps above:

1. Factor the denominators of the rational expressions.

x – 1 cannot be factored further. Meanwhile, since x² – 1 is a difference of two squares, we can factor it as (x + 1)(x – 1).

2. Write the factors of the denominators. Match the common factors in columns

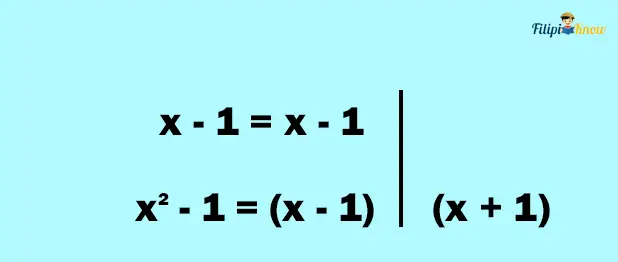
3. Bring down each factor in every column. Common factors in the column must be brought down also

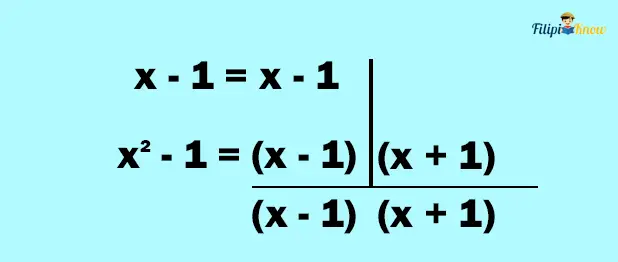
4. Multiply the factors you brought down. The resulting expression is the LCD

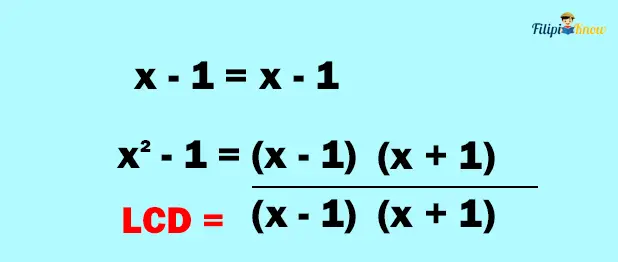
Thus, the LCD is (x + 1)(x – 1) or x² – 1.

Example 2:

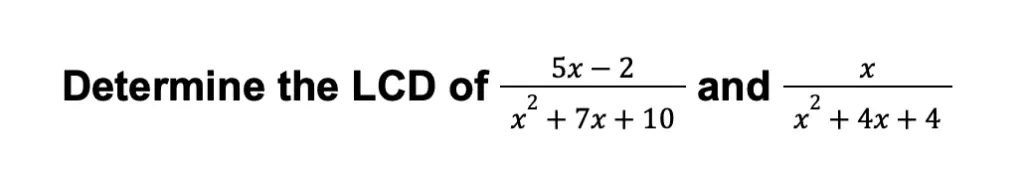
Solution:

1. Factor the denominators of the rational expressions.

x² + 7x + 10 can be factored as (x + 5)(x + 2). Meanwhile, x² + 4x + 4 can be factored as (x + 2)(x + 2).

2. Write the factors of the denominators. Match the common factors in columns

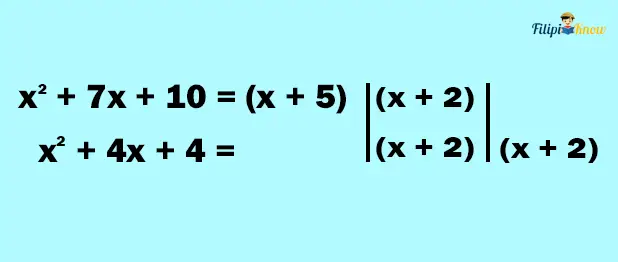
3. Bring down each factor in every column. Common factors in the column must be brought down also

4. Multiply the factors you brought down. The resulting expression is the LCD

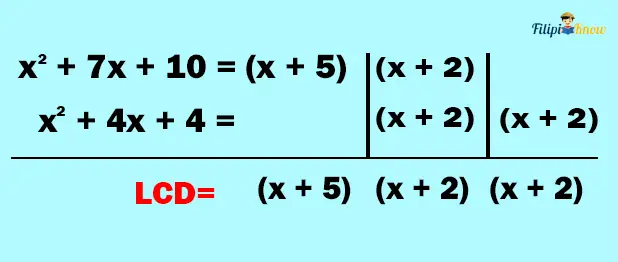
Based on our computations above, the LCD of x² + 7x + 10 and x² + 4x + 4 is (x + 2)(x + 2)(x + 5).

Note: When we are determining the LCD of two rational expressions, it is advisable to write the obtained LCD in factored form since expressions are much easier to multiply and divide if they are in factored form.

Make sure that you already mastered the skill of determining the LCD of rational expressions before proceeding to the actual process of adding and subtracting them.

Operations on Rational Expressions

In this section, we’ll discuss how to add, subtract, multiply, and divide rational expressions.

1. Addition and Subtraction of Rational Expressions

The process of adding and subtracting rational expressions is actually similar to the process of adding and subtracting fractions. Thus, if you know how to add or subtract fractions, then adding and subtracting rational expressions will not be so strange to you.

The first thing you have to do when adding or subtracting rational expressions is to look at their denominators. If the denominators are the same, then we can just add the numerators of the rational expressions and then copy the denominator. 

a. Addition and Subtraction of Rational Expressions With the Same Denominator

Here are the steps in adding rational expressions with the same denominator:

1. Add the numerators of the rational expressions. The resulting expression is the numerator of the answer.
2. Copy the common denominator and use it as the denominator of your answer.
3. Simplify the resulting rational expression, if possible.

Formally,

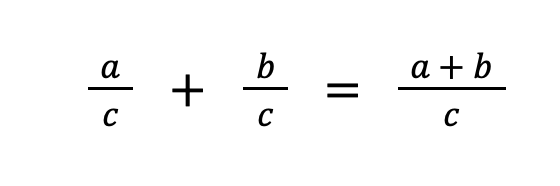
Example 1:

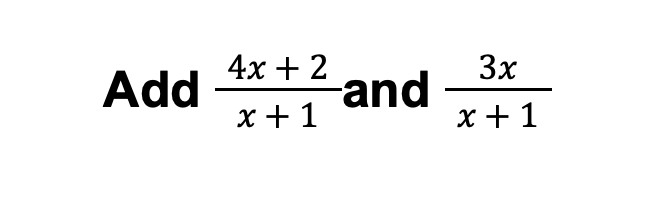
Solution:

1. Add the numerators of the rational expressions. The resulting expression is the numerator of the answer

2. Copy the common denominator and use it as the denominator of your answer

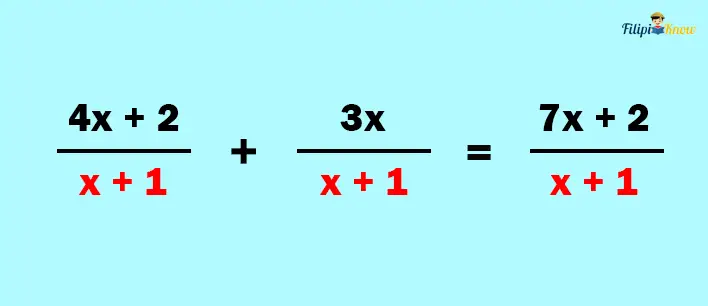
3. Simplify the resulting rational expression, if possible

In this case, we can’t simplify the resulting rational expression further so it automatically becomes the final answer.

Example 2:

Solution:

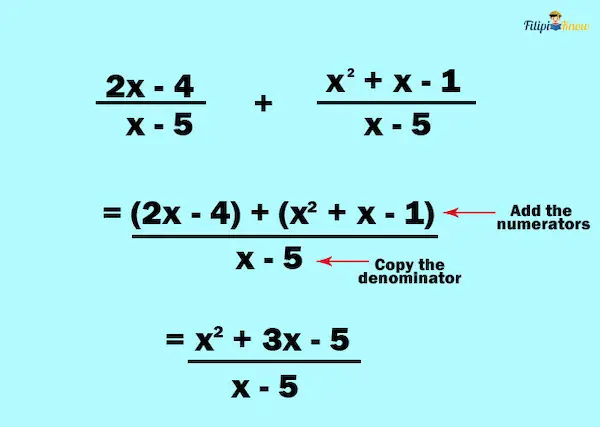
Example 3:

Solution:

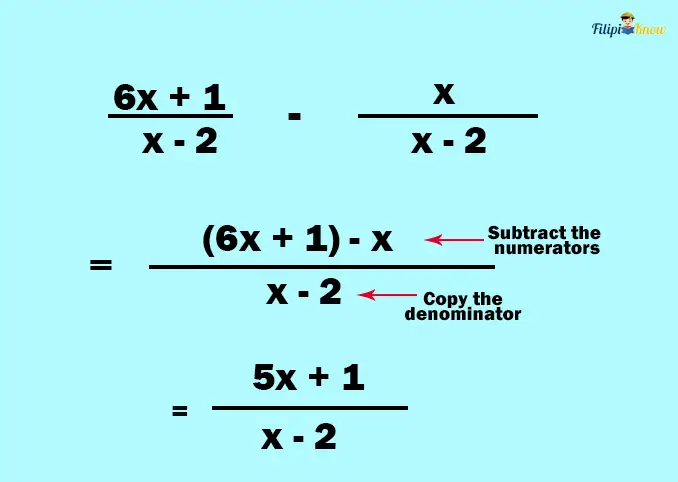
Example 4:

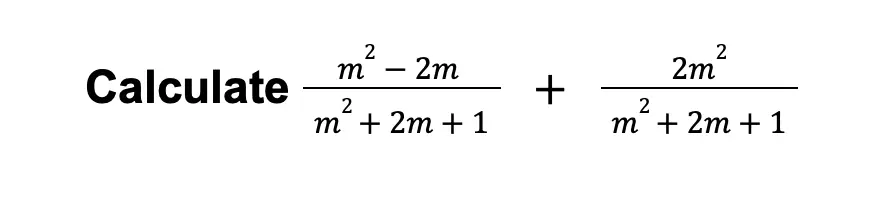
Solution:

Example 5:

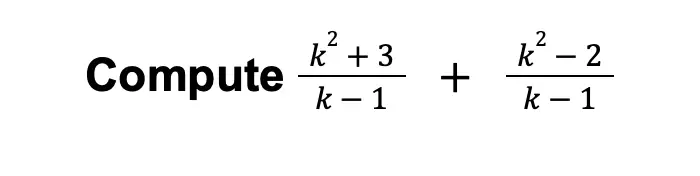
Solution:

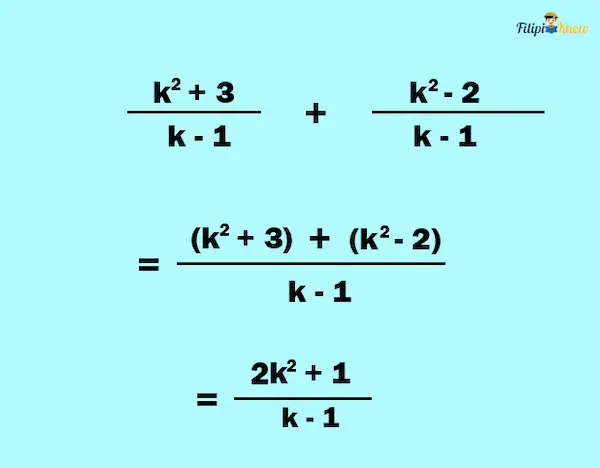
Now that you know how to add and subtract rational expressions with the same denominators, our next goal is to learn how to add and subtract rational expressions with different denominators.

b. Addition and Subtraction of Rational Expressions With Different Denominators.

To add or subtract rational expressions with different denominators, follow these steps:

1. Determine the LCD of the rational expressions.
2. Express the given rational expressions using the LCD you have obtained by dividing the LCD by the denominator of the rational expression and then multiplying the result to the numerator of the rational expression. The results will be the new numerators of the rational expressions.
3. Add or subtract the rational expressions you have obtained from the second step. Simplify the resulting expression, if possible.

Let us try to apply these steps to our examples below:

Example 1:

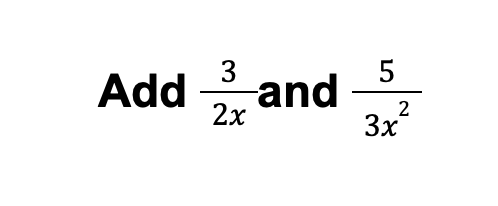
Solution:

Using the steps we have mentioned above on adding and subtracting rational expressions with different denominators, we’ll be able to obtain the answer.

1. Determine the LCD of the rational expressions.

2. Express the given rational expressions using the LCD you have obtained by dividing the LCD by the denominator of the rational expression and then multiplying the result to the numerator of the rational expression. The results will be the new numerators of rational expressions.

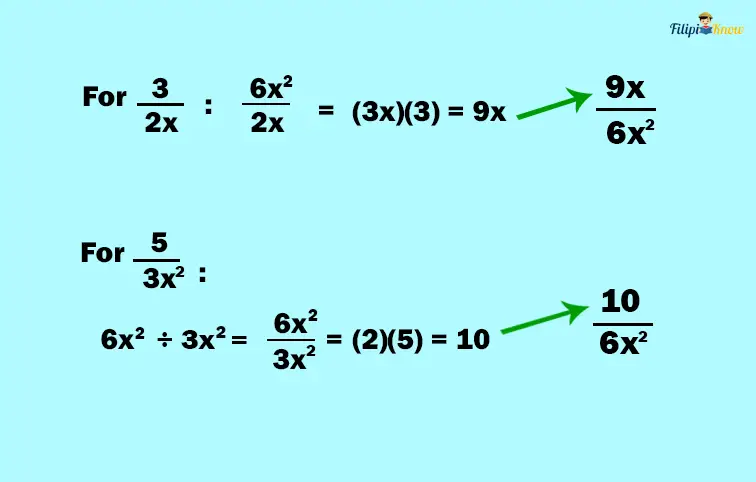
3. Add or subtract the rational expressions you have obtained from the second step. Simplify the resulting expression, if possible.

Example 2:

Solution:

1. Determine the LCD of the rational expressions.

The LCD is (x – 1)(x + 1).

2. Express the given rational expressions using the LCD you have obtained by dividing the LCD by the denominator of the rational expression and then multiplying the result to the numerator of the rational expression. The results will be the new numerators of rational expressions.

3. Add or subtract the rational expressions you have obtained from the second step. Simplify the resulting expression, if possible.

Example 3:

Solution:

1. Determine the LCD of the rational expressions

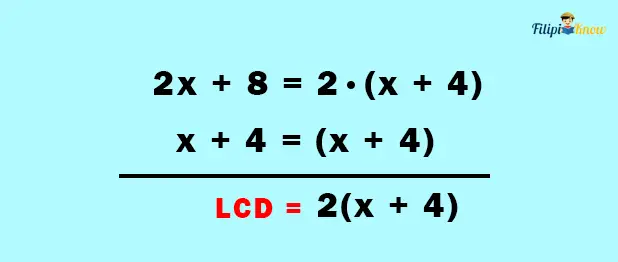
2. Express the given rational expressions using the LCD you have obtained by dividing the LCD by the denominator of the rational expression and then multiplying the result to the numerator of the rational expression. The results will be the new numerators of the rational expressions.

3. Add or subtract the rational expressions you have obtained from the second step. Simplify the resulting expression, if possible.

2. Multiplication of Rational Expressions

The steps in multiplying rational expressions are actually similar to the steps in multiplying fractions. Here are the steps:

1. Multiply the numerators of the rational expressions. Write the answer as the numerator of the resulting expression.
2. Multiply the denominators of the rational expressions. Write the answer as the denominator of the resulting expression.
3. Simplify the resulting expression, if possible.

Example:

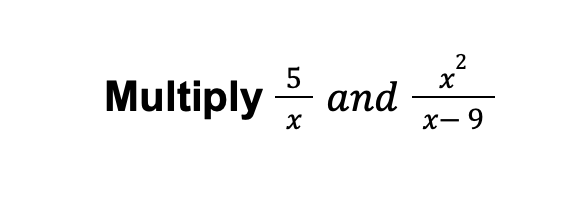
Solution:

Using the steps in multiplying rational expressions:

1. Multiply the numerators of the rational expressions. Write the answer as the numerator of the resulting expression.

2. Multiply the denominators of the rational expressions. Write the answer as the denominator of the resulting expression.

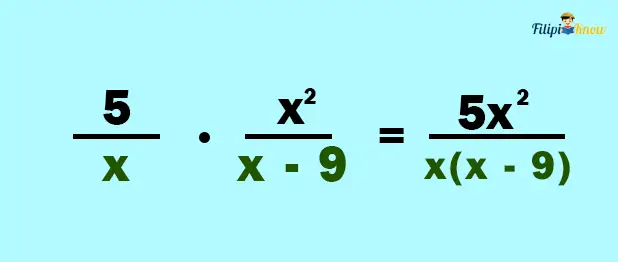
We will not perform distributive property in this case since we are simplifying the expression in the next step.

3. Simplify the resulting expression, if possible.

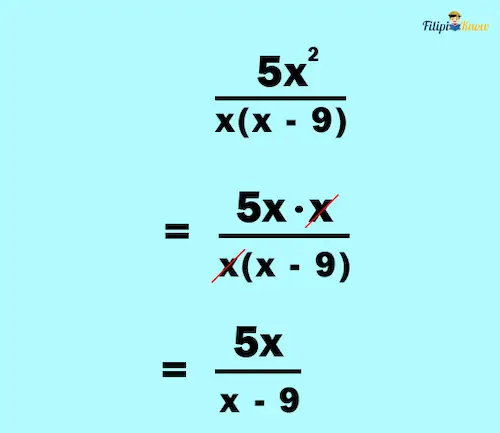
Using Cancellation Method in Multiplying Rational Expressions

Just like fractions, we can also apply the cancellation method to cancel out common factors among the given expressions to make our computation much easier. Let us try to apply this technique in our next examples.

Example 1: Apply the cancellation method to calculate the product of

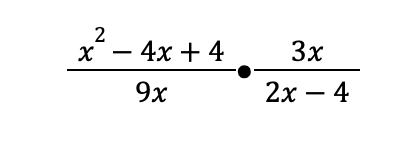
Solution:

Example 2:

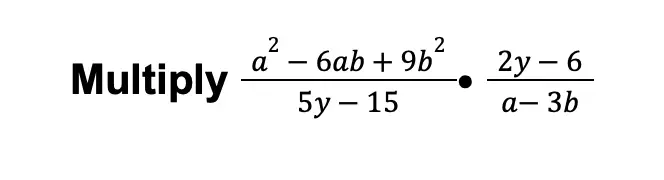
Solution:

3. Division of Rational Expressions

If you still remember how to divide fractions, dividing rational expressions will be easier because the steps are actually similar. Otherwise, here are the steps you need to remember when dividing rational expressions:

1. Get the reciprocal of the divisor or the second rational expression.
2. Multiply the rational expression you have obtained in Step 1 by the first rational expression.
3. Simplify the result, if possible.

Example 1:

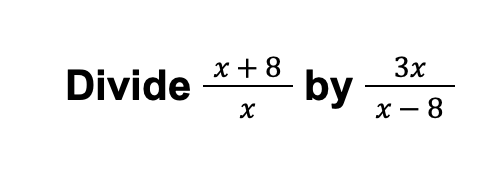
Solution:

1. Get the reciprocal of the divisor or the second rational expression.

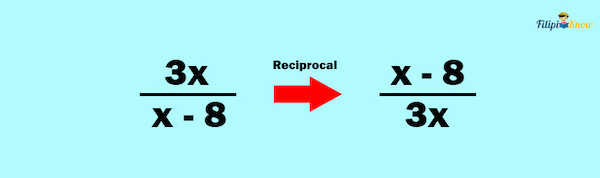
2. Multiply the rational expression you have obtained in Step 1 by the first rational expression.

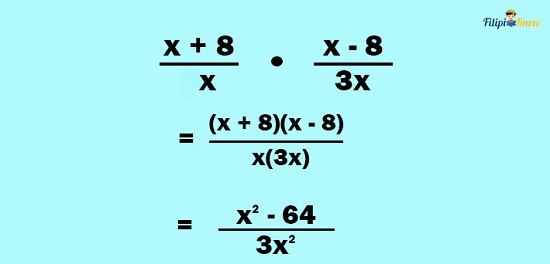
3. Simplify the result, if possible.

The result is already in simplified form, so we can skip this step.

Example 2:

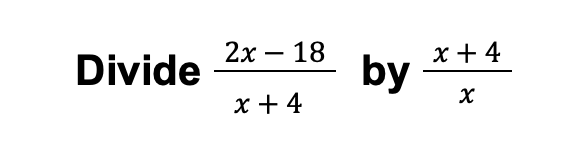
Solution:

Next topic: Radical Expressions

Previous topic: Quadratic Equations

Return to the main article: The Ultimate Basic Math Reviewer

Download Printable Summary/Review Notes

Download Printable Flashcards

Test Yourself!

1. Practice Questions [Free PDF Download]

2. Answer Key [Free PDF Download]

3. Math Mock Exam + Answer Key