How To Solve Linear Equations
Algebra is like solving a puzzle that challenges you to find a missing piece. In the case of algebra, that missing piece comes as an unknown value.
The previous chapters of this algebra review focused on how to compute algebraic expressions, but we haven’t started the “puzzle-solving” part yet.
Solving equations is the “puzzle-solving” part of algebra. In this chapter, you’ll learn how to find the value of an unknown variable of a linear equation, just like looking for a missing piece in a puzzle.
Click below to go to the main reviewers:
Ultimate Civil Service Exam Reviewer
Ultimate PMA Entrance Exam Reviewer
Ultimate PNP Entrance Exam Reviewer
Table of Contents
What Is an Equation?
An equation is a mathematical statement that tells you that two quantities are equal in value.
To determine whether a mathematical statement is an equation, look for the equal sign (=). If there’s a presence of an equal sign, then the mathematical statement is an equation.
For instance, 3 + 3 = 6 is an equation because it has an equal sign. 3 + 3 = 6 tells us that the value of 3 + 3 is equivalent to the value of 6.
Example: Which of the following are equations?
a. 2x + 3 = – 9
b. x = – 7
c. x – 5
Solution: The mathematical statements in a and b are equations because they have an equal sign. On the other hand, c is not an equation because of the absence of an equal sign.
In an equation, it is essential to recognize its left and right sides.
- The left-hand side of the equation – quantities on the left of the equal sign.
- The right-hand side of the equation – quantities on the right of the equal sign.
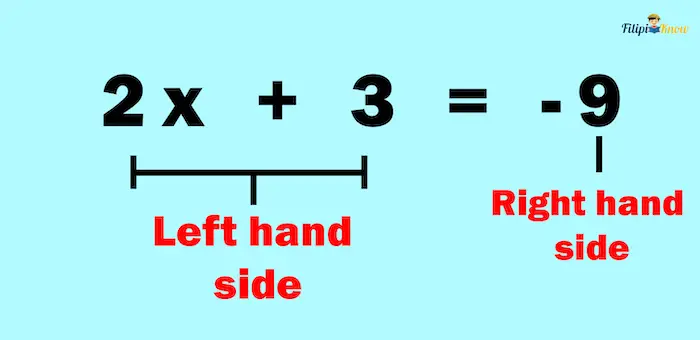
In the above example, the left-hand side of the equation 2x + 3 = -9 is 2x + 3, while its right-hand side is -9.
The Solution to an Equation
An equation involves a variable or a value that is unknown or not determined yet. When we say “solve an equation,” we mean to determine the value that unknown variable represents to make the equation hold.
For example, x + 9 = 10 is an equation telling us that x + 9 must be equivalent to 10.
x is the unknown variable in the equation. When we solve for x + 9 = 10, we determine the value of x so that x + 9 equals 10.
If x = 1, the left-hand side of the equation and the right-hand side of the equation will be of the same value.
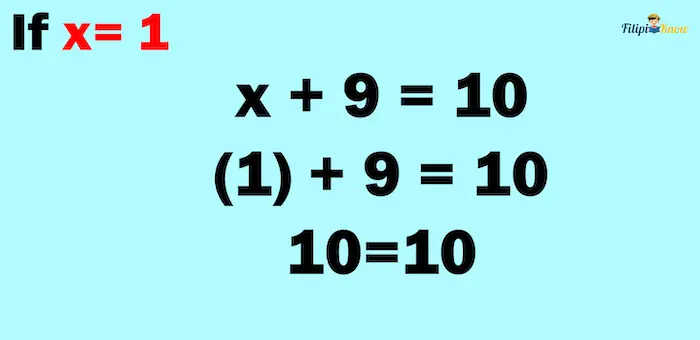
Once we have shown that the equation’s left-hand and right-hand sides are equal, the value of the variable we used is the solution to the equation. Therefore, the solution to the equation x + 9 = 10 is x = 1.
On the other hand, let’s say we use x = 2 for x + 9 = 10
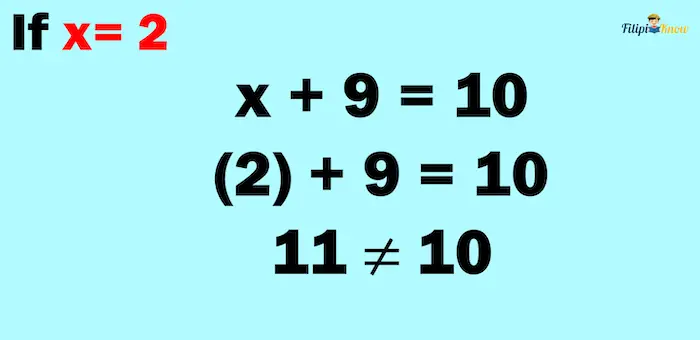
In this case, the left and right sides are not equal. Thus, x = 2 is not the solution to the equation x + 9 = 10.
Therefore, the solution to an equation is the value of the unknown variable that will make the equation true. When we say that the equation is true, it means that the left-hand side and the right-hand side of it are equal in value.
Example: Is x = 5 the solution to x + 2 = 7?
Solution: Yes, because if we substitute x = 5 to x + 2 = 7:
x + 2 = 7
(5) + 2 = 7
7 = 7
The left-hand side and the right-hand side of the equation are equal. Indeed, x = 5 is the solution to x + 2 = 7.
An equation is a puzzle with a missing piece. That missing piece is the unknown variable. When you solve for the value of the unknown variable, you are looking for the missing piece that will complete the puzzle or the equation.
But how do we find that missing piece? How do we find the solution to the equation?
The answer is we apply the properties of equality to solve an equation. In this reviewer’s next section, we will discuss these properties.
Properties of Equality
The properties of equality are rules or principles that allow us to manipulate equations to determine the values of the unknown variable. We can use the properties of equality as the logical explanation for why we manipulate an equation in a certain way.
Here are the properties of equality:
1. Reflexive Property of Equality
For any real number p:
p = p
This property is pretty evident and logical. The value of a number is always equal to itself.
For instance, 1020 will always be equal to 1020. If someone tells you that 1020 = 1100, he is logically false since 1020 is always equal to 1020 by the reflexive property.
2. Symmetric Property of Equality
For any real numbers p and q:
If p = q, then q = p
This property tells us that if we switch the positions of the quantities on the left-hand side and the right-hand side of the equation, the equation will still hold. This also implies that both sides of the equation are of the same value.
For example, 3 + 4 = 1 + 6 is true. By the symmetric property of equality, 1 + 6 = 3 + 4 must also be true.
3. Transitive Property of Equality
For any real numbers p, q, and r:
If p = q and q = r, then p = r
The transitive property of equality tells us that if a quantity is equal to a second quantity, and if the second quantity is equal to a third quantity, then we can conclude that the first quantity is equal to the third quantity.
For example, if we assume that x = y and y = w, then by the transitive property, we can conclude that x = w.
Another example: We know that 10 – 5 = 2 + 3 is true. We also know that 2 + 3 = 9 – 4. By the transitive property, we can conclude that 10 – 5 = 9 – 4.
4. Addition Property of Equality (APE)
For any real numbers p, q, and r:
If p = q, then p + r = q + r
APE tells us that the result will still be equal if we add a specific number to two equal quantities.
For example, 5 + 2 = 6 + 1 is true. Suppose that we add 8 to both sides of the equation:
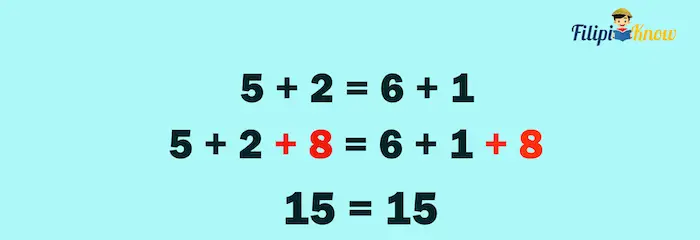
Notice that the resulting quantities are still equal even after adding the same number to both quantities.
APE implies that adding the same number to two equal quantities retains their equality.
5. Subtraction Property of Equality (SPE)
For any real numbers p, q, and r:
If p = q, then p – r = q – r
What if we subtract the same number from two equal quantities? Will equality be retained?
The equality will remain if we subtract a number from two equal quantities.
For instance, 5 + 2 = 6 + 1 is true. Suppose that we subtract two from both sides of the equation:
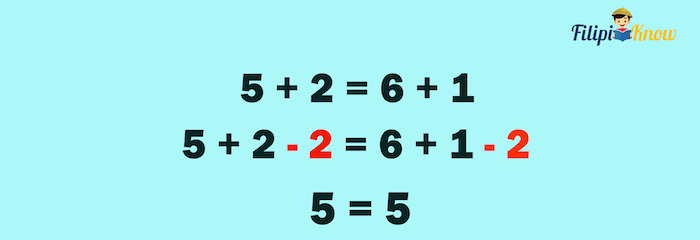
As we can see above, equality is retained.
SPE tells us that if we subtract two equal quantities by the same number, the results will still be equal.
6. Multiplication Property of Equality (MPE)
For any real numbers p, q, and r:
If p = q, then pr = qr
MPE tells us that the results will still be equal if we multiply two equal quantities by the same number.
For example, we know that 2 + 2 = 3 + 1. Suppose that we multiply both sides of this equation by 5:
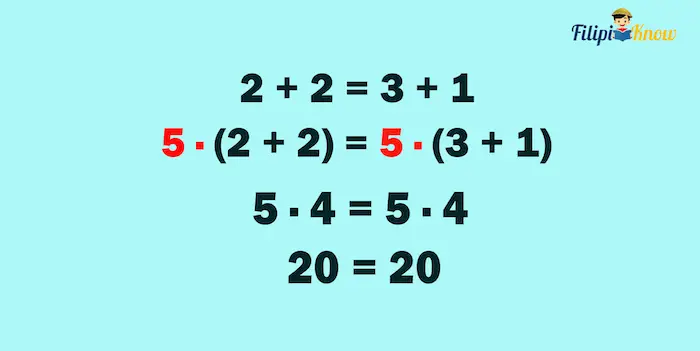
As shown above, the results will still be equal even after multiplying both sides by the same number.
7. Division Property of Equality
For any real numbers p, q, and r where r ≠ 0:
If p = q, then p/r = q/r
This property tells us that the results will still be equal if we divide two equal quantities by the same number (that number can be any number but must not be equal to 0).
For example, we know that 9 = 8 + 1. Suppose that we divide both sides of this equation by 3:
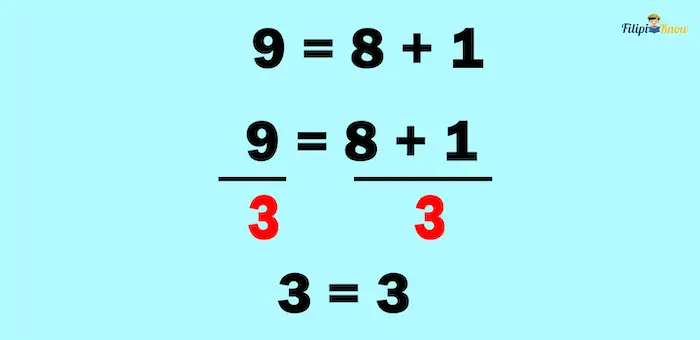
As per the division property of equality, the results are still equal.
8. Distributive Property of Equality
For any real numbers p, q, and r:
p(q + r) = pq + pr
You most likely remember learning about this in the previous reviewer (i.e., multiplication of polynomials). This property tells us that multiplying the sum of two or more addends equals the result when we multiply the addends by that number and add them.
For example, suppose we want to double the sum of 3 and 5. We can express it as:
2(3 + 5)
By the distributive property, we can distribute 2 to each addend and preserve equality.
2(3) + 2(5)
Now, 2(3) + 2(5) = 16. Hence, 2(3 + 5) = 2(3) + 2(5) = 16
9. Substitution Property of Equality
If x = y, then either x or y can be substituted into any equation for the other.
Suppose that x + y = 12. Assuming that x = y, we can replace y with x, and the equation will still hold.
Thus, if x = y, then x + y = 12 can be x + x = 12 or y + y = 12.
Here’s a table that summarizes the properties of equality:
| Property of Equality (Suppose that p, q, and r are real numbers) | Summary |
| Reflexive Property | p = p |
| Symmetric Property | If p = q, then q = p |
| Transitive Property | If p = q and q = r, then p = r |
| Addition Property of Equality | If p = q, then p + r = q + r |
| Subtraction Property of Equality | If p = q, then p – r = q – r |
| Multiplication Property of Equality | If p = q, then pr = qr |
| Division Property of Equality | If p = q, then p/r = q/r where r 0 |
| Distributive Property of Equality | p(q + r) = pq + pr |
| Substitution Property of Equality | If x = y and ax + by = c, then ax + bx = c or ay + by = c |
We will use the properties above to manipulate equations and determine the value of an unknown variable. In other words, these properties will be used to find the solution to an equation.
Linear Equations in One Variable
The first type of equation that we will learn how to solve is linear equations in one variable. These equations are the simplest type of equations and the easiest ones to answer.
Linear equations are equations such that the highest exponent of its variable is 1. The type of linear equations we will solve in this section is those with one variable only (linear equations with more than one variable will be discussed in the later sections).
For example, x + 3 = 9 is a linear equation since the highest exponent of its variable is 1. As you can notice, x + 3 = 9 has only one variable involved (which is x). Thus, x + 3 = 9 is a linear equation in one variable.
In other words, linear equations in one variable are in ax + b = c form, where a, b, and c are real numbers and a ≠ 0.
Example: Which of the following are linear equations in one variable?
a. 2x + 7 = 19
b. x2 + 6x + 9 = 0
c. x + y = 2
Solution: The equation in a is the only linear equation in one variable among the given equations since the highest exponent of its variable is one, and it has only one variable. The equation in b is not linear since the highest exponent of its variable is 2 (it is a quadratic equation). Meanwhile, the equation in c, although the highest exponent of its variable is 1, is not linear in one variable because two variables are involved (i.e., x and y).
Furthermore, note that the equation in a is the only equation in the form ax + b = c form.
In the next section, you will learn how to solve linear equations in one variable by applying the equality properties discussed above.
How To Solve Linear Equations in One Variable
Example 1: Let us try to solve for the value of x in x – 9 = 10.
Solution: To find the value of x, we aim to isolate the variable from the constants. If we want to solve for x, then x must be the only quantity on the left side of the equation, and the other quantities must be on the right side. But how can we achieve that?
x will be the only quantity on the left if we eliminate -9 on the left side. How can we then remove -9 on the left side?
The addition property of equality (APE) states that we can add the same number to both sides of the equation.
Applying the APE, we can add 9 to both sides of the equation so we can cancel -9 on the left side:
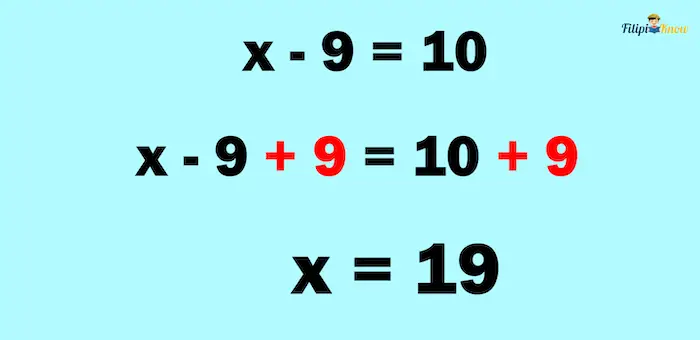
Now, it is seen that x = 19.
That’s it! We have solved the value of x in x – 9 = 10. The answer is x = 19.
Example 2: Solve for x in x – 12 = 22
Solution:
x – 12 = 22
x – 12 + 12 = 22 + 12 (Adding 12 to both sides of the equation)
x = 34
Hence, x = 34.
Note that the explanation for why it is valid to add 12 to both sides of the equation is that we apply the addition property of equality.
Example 3: Solve for x in x + 10 = 52
Solution: To isolate x from the constants, we must eliminate 10 by subtracting 10 from both sides of the equation. Subtracting the same number from both sides of the equation is valid because of the subtraction property of equality (SPE) discussed earlier.
x + 10 = 52
x + 10 – 10 = 52 – 10 (Subtracting 10 from both sides of the equation)
x = 42
Thus, the answer is x = 42
Transposition Method
We can use a “shortcut” method instead of applying the APE or SPE. To isolate x from the constants, we can transpose the constant to the right-hand side of the equation so that x will be the only quantity that will remain on the left side.
Example 1: Let us solve x + 9 = 10 using the transposition method.
Solution:
We aim to isolate x from other constants by transposing 9 to the right-hand side of the equation. Once a quantity “crosses” the equality sign, its sign reverses (i.e., from positive 9 to -9).
After transposing 9 to the right-hand side and reversing its sign, we add it to the quantity on the right-hand side (10).
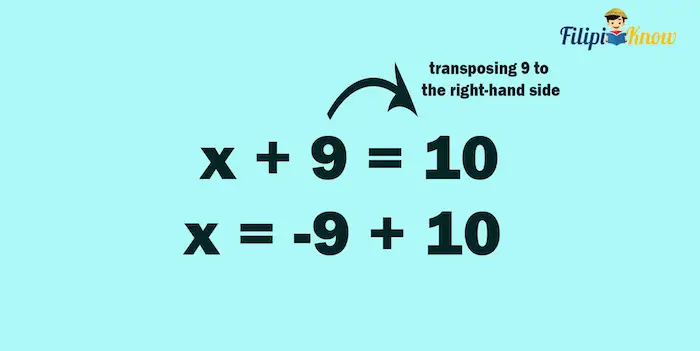
Then, we perform some arithmetic:
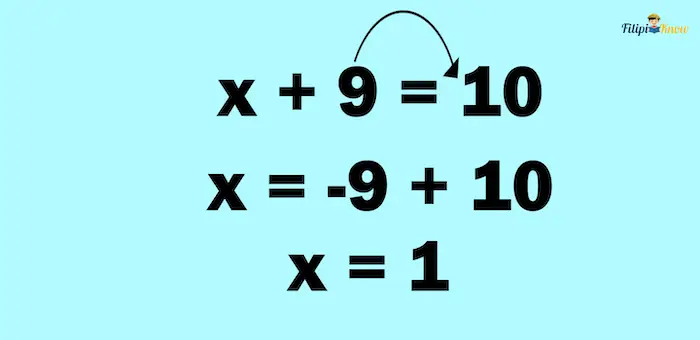
Thus, the answer is x = 1.
Example 2: Use the transposition method to solve for x in x – 9 = 12.
Solution: Transposing -9 to the right-hand side will reverse its sign (i.e., from negative to positive):
x = 9 + 12
x = 21
Thus, the answer is x = 21.
Example 3: Solve for x in x + 6 = 5 using the transposition method.
Solution: Transposing 6 to the right-hand side will reverse its sign (i.e., from positive to negative):
x = – 6 + 5
x = – 1
Thus, the answer is x = -1.
Example 4: Solve for x in x – 4 = – 9 using the transposition method.
Solution:
x – 4 = -9
x = 4 + (- 9) (Transposing -4 to the right-hand side will change its sign to positive)
x = -5
Thus, the answer is x = -5.
Note: In this review, we will use the transposition method more frequently to isolate x from other quantities. The transposition method is more convenient than adding numbers to or subtracting numbers from both sides of the equation.
Applying the Division Property of Equality to Solve Linear Equations in One Variable
Most of the linear equations in one variable we have solved above are in ax + b = c form where a = 1 (the coefficient of x is 1) But what if a is not equal to 1 like in 2x + 4 = 6? If this is the case, we can solve for x by applying the division property of equality.
Example 1: Let us try to solve for x in 2x + 4 = 6.
Solution: Again, to solve for x in an equation, it must be isolated from the constants, or x should be the only quantity on the left-hand side of the equation.
Let us start by getting rid of 4 on the left-hand side by using the transposition method:
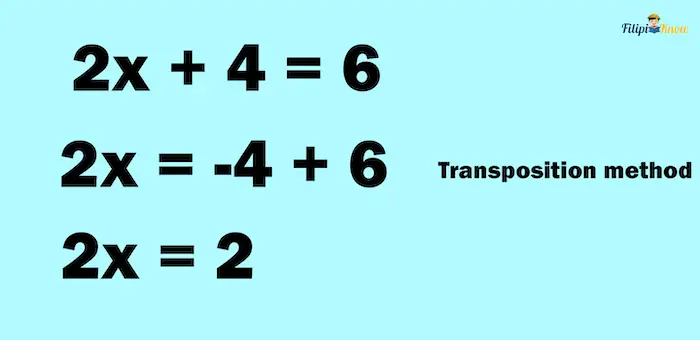
What is left is 2x = 2. Again, we aim to make x the only quantity on the left-hand side. This means that we need to cancel out 2 in 2x. But how do we cancel it?
We can divide both sides of the equation by two to cancel two in 2x. This is valid because equality’s division property guarantees that dividing both sides of the equation by the same number will preserve equality.

As we can see, the answer is x = 1.
Here’s a quick preview of what we have done above:
2x + 4 = 6
2x = -4 + 6 (Transposing 4 to the right-hand side will turn it into -4)
2x = 2
2x⁄2 = 2⁄2 (Dividing both sides of the equation by 2)
x = 1
Thus, the solution to 2x + 4 = 6 is x = 1
You can verify that x = 1 is the solution by substituting it back to 2x + 4 = 6. Notice that the equation will be true if x = 1:
2(1) + 4 = 6
2 + 4 = 6
6 = 6
Example 2: Solve for x in 3x – 18 = 27
Solution: To solve for x, x should be the only quantity on the left-hand side.
We start by transposing -18 to the right-hand side. If we transpose it, it will have a positive sign.
3x = 18 + 27
3x = 45
To cancel out 3 in 3x, we divide both sides of the equation by 3:
3x⁄3= 45⁄3
x = 15
Therefore, the answer is x = 15
Example 3: Solve for x in 4x – 18 = 2
Solution: To solve for x, x should be the only quantity on the left-hand side.
We start by transposing -18 to the right-hand side. If we transpose it, it will change its sign from negative to positive.
4x = 18 + 2
4x = 20
To cancel out 4 in 4x, we divide both sides of the equation by 4:
4x⁄4= 20⁄4
x = 5
Therefore, the answer is x = 5.
Example 4: Solve for x in 7x + 2 = 16
Solution:
7x + 2 = 16
7x = -2 + 16 Transposition Method (we transpose 2 to the right-hand side)
7x⁄7= 14⁄7 Division Property of Equality (divide both sides of the equation by 7)
x = 2
More Examples of Solving Linear Equations in One Variable
This section contains more linear equations in one variable to solve. However, these equations are trickier than we have solved since they appear in different forms. Just remember three things so you can solve them: the properties of equality, the transposition method, and our goal to isolate x from other constants (or x should be the only quantity on the left-hand side).
Example 1: Solve for x in 3x – 3 = x + 5
Solution: Let us put all x first on the left-hand side. We can do this by transposing the x on the right-hand side to the left-hand side. Like numbers, variables will also reverse their sign once they cross the equality sign.
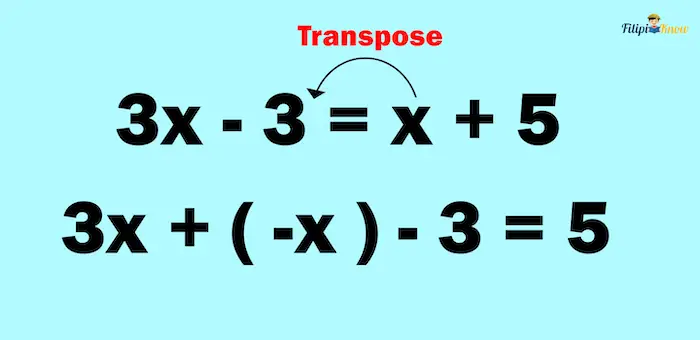
We can then combine 3x and -x to obtain 2x:
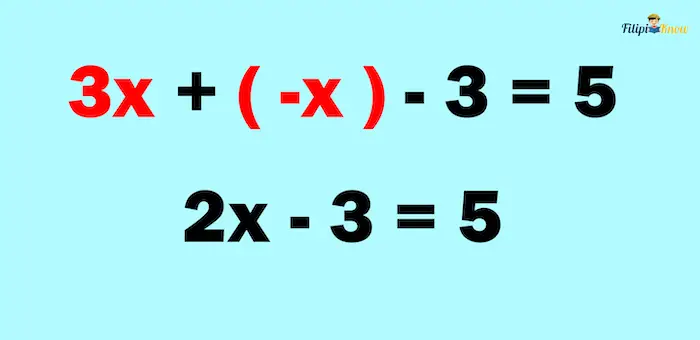
Now, we have 2x – 3 = 5. We can apply the techniques we have learned above to solve this one:
2x – 3 = 5
2x = 3 + 5 Transposition Method
2x = 8
2x⁄2= 8⁄2 Division Property of Equality
x = 4
Example 2: Solve for 9 – x = 2x – 3
Solution: We start by putting all x on the left-hand side of the equation using the transposition method.
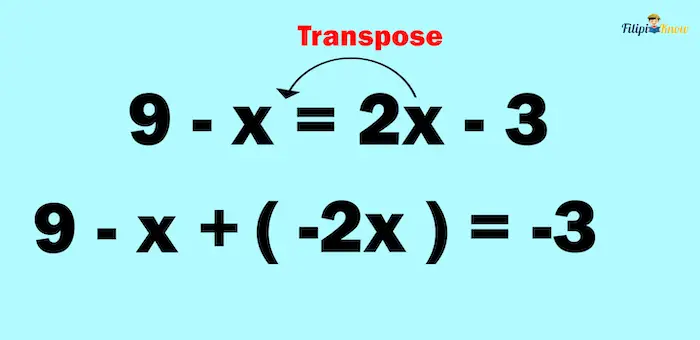
We can then combine -2x and -x to obtain -3x:
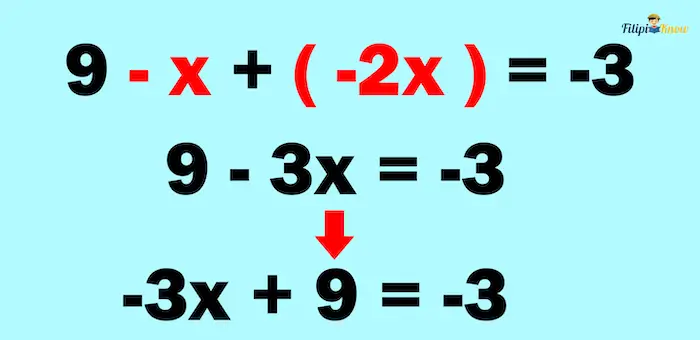
Thus, we have –3x + 9 = – 3. Let us now use the techniques we have learned to solve for x:
-3x + 9 = -3
-3x = -9 + (-3) Transposition Method
-3x = -12
–3x⁄-3= -12⁄-3 Division Property of Equality
x = 4
Example 3: Solve for 3(2x + 1) = 15
Solution: Since 3 is multiplied by the sum of addends, we can apply the distributive property so that our equation will be in ax + b = c form.
3(2x + 1) = 15
3(2x) + 3(1) = 15 Distribute 3 to 3(2x + 1)
6x + 3 = 15
Now, let us continue the process using the techniques we have learned in the previous sections:
6x = -3 + 15 Transposition Method
6x = 12
6x⁄6= 12⁄6 Division Property of Equality
x = 2
Therefore, the answer is x = 2
Example 4: Solve for x in
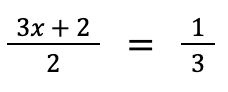
Solution: If a linear equation in one variable is fractional in form, we “remove” the denominator by multiplying both sides of the equation by the Least Common Denominator (this method is valid because of the multiplication property of equality).
The Least Common Denominator (LCD) is the lowest common multiple of the denominators 3 and 2. Therefore, the LCD should be 6.
We then multiply both sides of the equation by the LCD (which is 6):
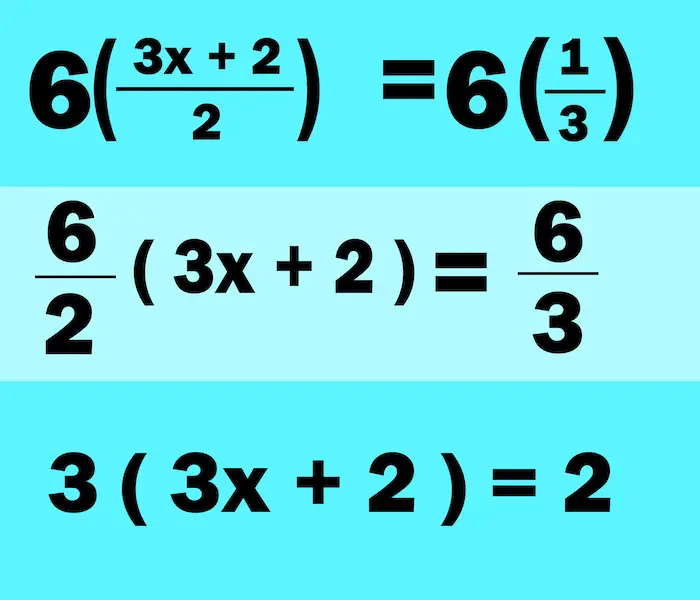
Now, our equation becomes 3(3x + 2) = 2
Let us continue solving for x:

x = -4/9
Therefore, the answer is x = -4/9
Example 5: Solve for x in
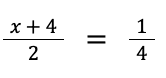
Solution:

x = -7⁄2
Solving Word Problems Using Linear Equations in One Variable
Now that you have learned the essential techniques and principles to solve linear equations in one variable, we can apply this skill to solve some word problems.
To solve word problems using linear equations, follow these steps:
- Read and understand the given problem and determine what is being asked.
- Represent the unknown in the problem using a variable.
- Construct a linear equation that will describe the problem.
- Solve for the value of the unknown variable in the linear equation.
Example 1: The sum of a number and 5 is – 3. What is the number?
Solution:
Step 1: Read and understand the problem and determine what is being asked. The problem asks us to determine the number such that the sum of that number and 5 is – 3.
Step 2: Represent the unknown in the problem using a variable. Let x represent the number we are looking for.
Step 3: Construct a linear equation that will describe the problem. The problem states that the sum of the unknown number (represented by x) and 5 is – 3. Therefore, we construct the linear equation below:
x + 5 = – 3
Step 4: Solve for the value of the unknown variable in the linear equation. Using the equation, we have derived from Step 3, we solve for the value of x:
x + 5 = – 3
x = – 5 + (-3) Transposition Method
x = -8
Thus, the number is -8.
Example 2: Fred has 52 books in his collection. He gave some of these books to Claude. Fred also gave books to Franz. The number of books that Fred gave to Franz is twice the number of books that he gave to Claude. The number of books left to Fred after he gave some to Claude and Franz is 22. How many books did Claude receive?
Solution:
Step 1: Read and understand the problem and determine what is being asked. The problem is asking us to determine the number of books Claude received from Fred.
Step 2: Represent the unknown in the problem using a variable. Let x be the number of books that Claude received. Since Franz received twice the number of books Claude received, we let 2x be the number Franz received.
To summarize:
- x = number of books that Claude received
- 2x = number of books that Franz received
Step 3: Construct a linear equation that will describe the problem. It’s stated that after Fred gave some books to Claude and Franz, there were only 22 books left.
We can express this statement this way:
52 – (number of books that Claude received) – (number of books that Franz received) = 22
Using the variables we have set in Step 2:
52 – x – 2x = 22
Step 4: Solve for the value of the unknown variable in the linear equation.
52 – x – 2x = 22
52 – 3x = 22 Combining like terms
-3x = -52 + 22 Transposition Method
-3x = -30
-3x⁄-3= -30⁄-3 Division Property of Equality
x = 10
Since x represents the number of books Claude received from Fred, then Claude received ten books from Fred.
Using the value of x we obtained in the problem, can you determine how many books Franz received from Fred?
The answer is 20 since Franz received twice the number of books Claude received.
Example 3: The total number of participants in a mini-concert by a local band is 300. The number of female participants in the mini-concert is half the number of male participants in the event. How many male participants are there in the mini-concert?
Solution:
Step 1: Read and understand the problem and determine what is being asked. The problem is asking us to determine the number of male participants in the mini-concert.
Step 2: Represent the unknown in the problem using a variable. Let x be the number of male participants in the mini-concert. Since the number of female participants in the mini-concert is half the number of male participants, we let ½ x represent the number of female participants in the event.
Step 3: Construct a linear equation that will describe the problem. The total number of participants in the mini-concert is 300. We can express this as:
(Number of Male Participants) + (Number of Female Participants) = 300
Using the variables we have set in Step 2:
x + ½ x = 300
Step 4: Solve for the value of the unknown variable in the linear equation.
Let us solve for x in x + ½ x = 300
x + ½ x = 300
2(x + ½ x) = 2(300) Multiplying both sides of the equation by the LCD
2(x) + 2(½ x) = 600 Distributive Property
2x + x = 600
3x = 600
3x⁄3= 600⁄3 Division Property of Equality
x = 200
Since x represents the number of male participants in the mini-concert, there are 200 male participants.
Linear Equations in Two Variables (Systems of Linear Equations)
As the name suggests, linear equations in two variables are linear equations with two variables involved. For instance, x + y = 5 is an example of a linear equation in two variables because two variables are involved (i.e., x and y).
Formally, linear equations in two variables are in ax + by = c form, where a, b, and c are real numbers and a and b are nonzero.
Solutions of Linear Equations in Two Variables
Linear equations in two variables have two solutions: one for x and one for y. For example, one possible solution for x + y = 5 is x = 2 and y = 3.
However, note that other x and y pairs will satisfy x + y = 5. For instance, the equation will be true if x = 0 and y = 5. Also, if x = 1 and y = 4, the equation will also be true. In other words, there are infinite values of x and y that will satisfy x + y = 5!
A linear equation with two variables has infinite possible x and y values. For this reason, we need another two or more linear equations in two variables that will provide us with a single pair of values of x and y only.
Let us add x – y = 1 in the discussion. For instance, if we solve for the values of x and y that satisfy x + y = 5 and x – y = 1 simultaneously, we obtain x = 3 and y = 2. Note that these x and y values are the only ones satisfying both x + y = 5 and x – y = 1.

The pair of equations x + y = 5 and x – y = 1 is called a system of linear equations.
A system of linear equations is composed of two or more linear equations. The solution of a system of linear equations will satisfy all of the equations in the system.
Again, the pair x + y = 5 and x – y = 1 is an example of a system of linear equations.
At x = 3 and y = 2, the equations are both satisfied:
x + y = 5
(3) + (2) = 5 at x = 3 and y = 2
5 = 5
x – y = 1
(3) – (2) = 1 at x = 3 and y = 2
1 = 1
Therefore, x = 3 and y = 2 is the solution of the system of linear equations x + y = 5 and x – y = 1.
How To Solve a System of Linear Equations
There are different ways of solving a system of linear equations. In this section, we will discuss two methods: the substitution method and the elimination method.
1. How To Solve a System of Linear Equations by Substitution
To solve a system of linear equations using the substitution method, follow these steps:
- Solve for the value of one variable in one of the linear equations in terms of the other variable.
- Substitute the expression for the variable you have obtained in Step 1 in the other linear equation.
- Solve for the value of the other variable in the equation you have obtained from Step 2.
- Plug in the value of the unknown variable you have computed in Step 3 in the expression you have obtained in Step 1 to find the value of the other variable.
The steps might be too abstract now, but they are easy to follow. Let us use these steps in our example below:
Example 1: Solve for the values of x and y that will satisfy x + y = 9 and x – y = 3
Solution:
Let us write first the given equations:
Equation 1: x + y = 9
Equation 2: x – y = 3
Step 1: Solve the value of one variable in one of the linear equations in terms of the other variable. Using Equation 1, we solve for the value of y in terms of x. This means we let y be the only quantity on the left side while the other quantities must be on the right side, including x. To make this possible, we transpose x to the right side:
x + y = 9 ⟶ y = – x + 9
Step 2: Substitute the expression for the variable you have obtained in Step 1 in the other linear equation. We have obtained y = -x + 9 in Step 1. What we are going to do is to substitute this value of y into the y in Equation 2:
x – y = 3 (Equation 2)
x – (-x + 9) = 3 (We substitute y = -x + 9)
Notice that once we substitute y = -x + 9 in Equation 2, Equation 2 will be a linear equation in one variable.
Step 3: Solve for the value of the other variable in the equation you have obtained from Step 2. The equation obtained in Step 2 is x – (-x + 9) = 3. Our goal now is to solve for x.
We use the techniques in solving linear equations in one variable:
x – (-x + 9) = 3
x + x – 9 = 3 Distributive Property
2x – 9 = 3
2x = 9 + 3 Transposition Method
2x = 12
2x⁄2= 12⁄2 Division Property of Equality
x = 6
Now that we have obtained the value for x, which is x = 6, let us solve for y.
Step 4: Plug in the value of the unknown variable you have computed in Step 3 in the expression you have obtained in Step 1 to find the value of the other variable. From Step 3, we have obtained x = 6. We substitute x to the equation obtained in Step 1, y = -x + 9.
y = -x + 9 (The expression we have obtained in Step 1)
y = -(6) + 9 (Substitute x = 6 which we have obtained in Step 3)
y = 3
That’s it! The solution for our system of linear equations is x = 6 and y = 3.
2. How To Solve a System of Linear Equations by Elimination
To solve a system of linear equations using the elimination method, follow these steps:
- Write the given equations in standard form.
- Add or subtract the given equations so that one variable will be eliminated. If no variable can be eliminated by adding or subtracting the equations, you may multiply an equation by a constant to allow the elimination of a variable.
- Solve for the value of the remaining variable.
- Substitute the value of the variable you have computed in Step 3 to any of the given equations, then solve for the value of the other variable.
Let us follow the above steps in our example below:
Example 1: Solve for the values of x and y that will satisfy x + y = 10 and x – y = 12
Solution:
Step 1: Write the given equations in standard form. If you recall, the standard linear equation in two variables is ax + by = c. Both x + y = 10 and x – y = 12 are already in standard form so we can skip this step.
Step 2: Add or subtract the given equations to eliminate one variable. If no variable can be eliminated by adding or subtracting the equations, you may multiply an equation by a constant to allow the elimination of a variable.
If we add the equations x + y = 10 and x – y = 12, the y variable will be eliminated. There’s no need to multiply the equations with a constant since we can immediately cancel a variable by adding the equations.
After adding the equations, the resulting equation will be 2x = 22
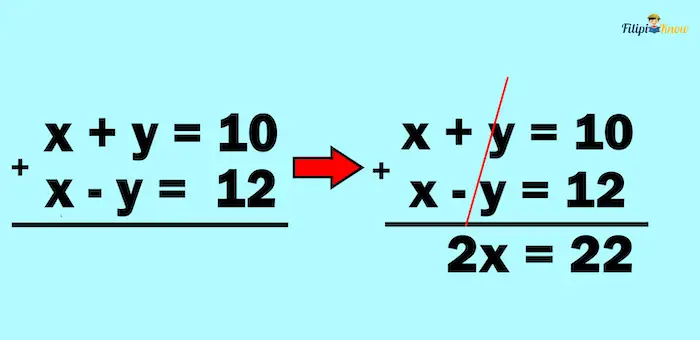
Step 3: Solve for the value of the remaining variable. The remaining variable in 2x = 22 is x. We solve for x in this step by dividing both sides of 2x = 22 by 2:
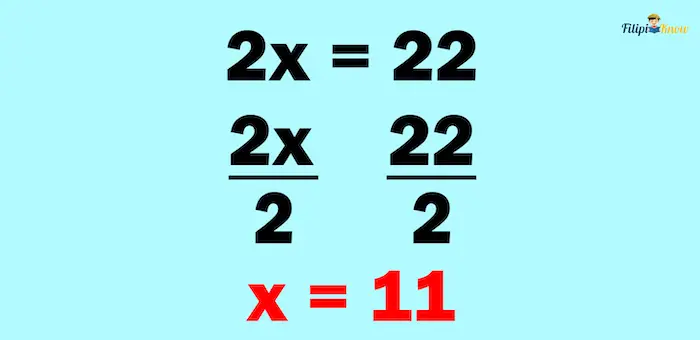
Thus, x = 11
Step 4: Substitute the value of the variable you have computed in Step 3 to any of the given equations, then solve for the value of the other variable. We substitute x = 11 into one of the given equations. Let us use x + y = 10:
x + y = 10
(11) + y = 10 Substituting x = 11
y = -11 + 10 Transposition Method
y = -1
Therefore, the solution for the system of linear equations is x = 11 and y = -1.
Next topic: Quadratic Equations
Previous topic: Special Products and Factoring
Return to the main article: The Ultimate Basic Math Reviewer
Download Printable Summary/Review Notes
Download Printable Flashcards
Test Yourself!
1. Practice Questions [Free PDF Download]
2. Answer Key [Free PDF Download]
3. Math Mock Exam + Answer Key
Written by Jewel Kyle Fabula
in Civil Service Exam, College Entrance Exam, LET, NAPOLCOM Exam, NMAT, PMA Entrance Exam, Reviewers, UPCAT
Jewel Kyle Fabula
Jewel Kyle Fabula graduated Cum Laude with a degree of Bachelor of Science in Economics from the University of the Philippines Diliman. He is also a nominee for the 2023 Gerardo Sicat Award for Best Undergraduate Thesis in Economics. He is currently a freelance content writer with writing experience related to technology, artificial intelligence, ergonomic products, and education. Kyle loves cats, mathematics, playing video games, and listening to music.
Copyright Notice
All materials contained on this site are protected by the Republic of the Philippines copyright law and may not be reproduced, distributed, transmitted, displayed, published, or broadcast without the prior written permission of filipiknow.net or in the case of third party materials, the owner of that content. You may not alter or remove any trademark, copyright, or other notice from copies of the content. Be warned that we have already reported and helped terminate several websites and YouTube channels for blatantly stealing our content. If you wish to use filipiknow.net content for commercial purposes, such as for content syndication, etc., please contact us at legal(at)filipiknow(dot)net
