Area and Perimeter Formulas

If you want to determine how many meters of fencing materials you need to enclose your backyard, you are asking for the perimeter of your backyard. On the other hand, if you want to determine how much a particular land property is, you need to know how many square meters it is; in this case, you are asking for that property’s area.
These are just a few examples of how significant the geometric concepts of area and perimeter are. These concepts are always involved in plane figures such as triangles, squares, rectangles, trapezoids, etc. Area and perimeter are the concepts we use to describe a particular plane figure quantitatively.
What does “perimeter” mean?? How about “area”? How do you compute the perimeter and area of plane figures? What are the area and perimeter formulas? These are the questions we are going to answer in this review.
Click below to go to the main reviewers:
Ultimate Civil Service Exam Reviewer
Ultimate PNP Entrance Exam Reviewer
Ultimate PMA Entrance Exam Reviewer
Table of Contents
Part I: Perimeter of a Plane Figure
The perimeter of a plane figure (a two-dimensional geometric figure) is the distance around it.
Take a look at Mang Berto’s rectangular garden:
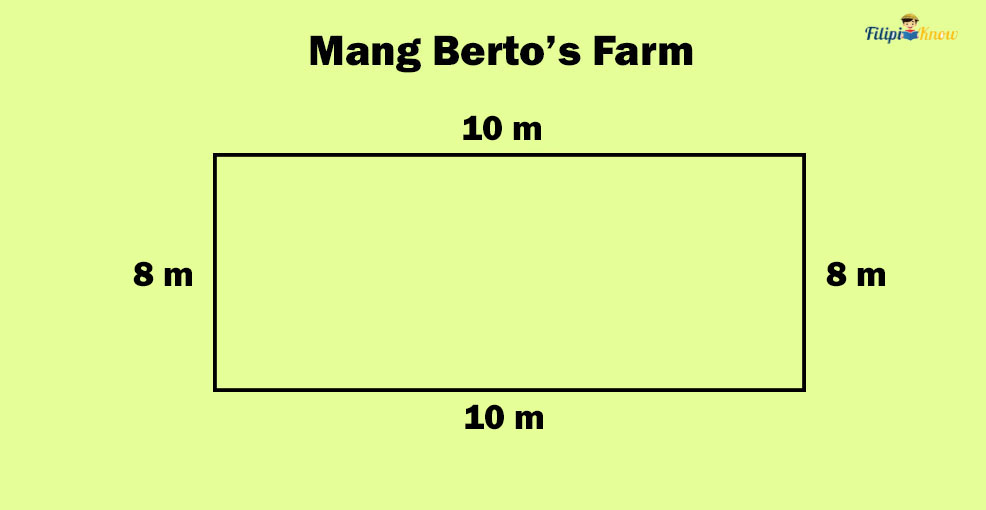
The total distance around Mang Berto’s rectangular farm can be calculated by adding all of the lengths of the sides of the rectangular farm.
Thus, the perimeter of Mang Berto’s rectangular farm is 8 m + 10 m + 8 m + 10 m = 36 m.
Based on our example above, the perimeter of a plane figure is just the sum of the lengths of its sides.
Sample Problems: Determine the perimeter of the following:
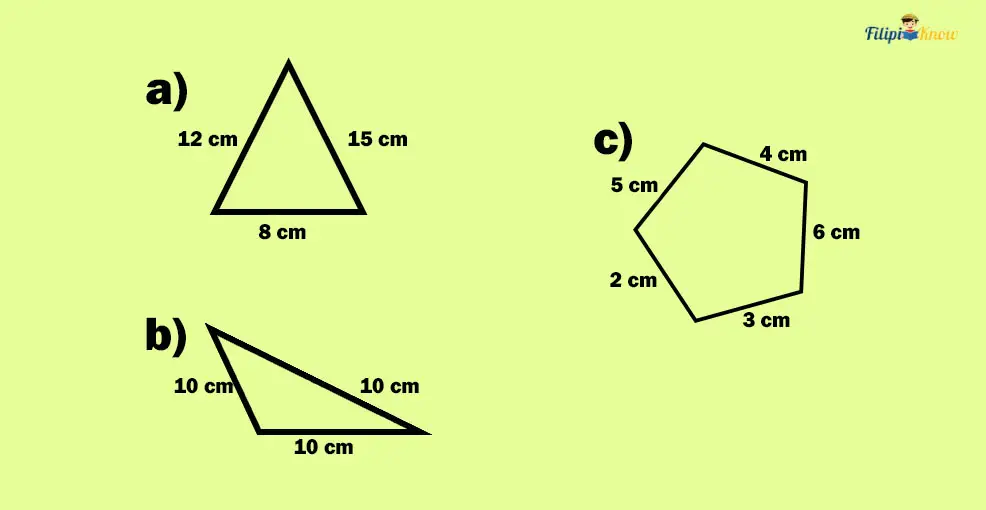
Solution:
a. 12 cm + 15 cm + 8 cm = 35 cm
b. 10 cm + 10 cm + 10 cm = 30 cm
c. 4 cm + 5 cm + 6 cm + 3 cm + 2 cm = 20 cm
Let us now discuss how to find the perimeter of the most common geometric plane figures.
Summary of Formulas for the Perimeter of Plane Figures
The table below provides an overview of how to find the perimeter of common geometric figures such as triangles, squares, or rectangles.
| Plane Figure | Formula for Perimeter |
| Triangle | P = a + b + c where a, b, and c are sides of the triangle P = 3s (if equilateral triangle) where s is a side of the equilateral triangle |
| Square | P = 4s where s is a side of the square |
| Rectangle | P = 2l + 2w or P = 2(l + w) where l and w are the length and the width of the rectangle, respectively |
Perimeter of a Triangle
The perimeter of a triangle is just the sum of its three sides:
Ptriangle = a + b + c
Where a, b, and c are sides of the triangle.

Now, if the given triangle is equilateral (which means that all of its sides are congruent or equal in measurement), then its perimeter can be calculated as:
Pequilateral triangle = 3s
Where s is a side of the equilateral triangle.
Sample Problem 1: Calculate the perimeter of a triangle whose sides have lengths of 10 cm, 12 cm, and 15 cm.
Solution:
Using the formula for the perimeter of a triangle:
P = a + b + c
P = 10 cm + 12 cm + 15 cm
P = 37 cm
Sample Problem 2: Mela cut a triangle from a cartolina paper. Mela wants her triangle to have sides that are all equal in length. A side of Mela’s triangle is 15 cm in length. Determine the perimeter of the triangle.
Solution: Mela’s triangle is equilateral since its sides are equal in length. To find the perimeter of an equilateral triangle, you can multiply the measurement of a side of a triangle by 3. A side of Mela’s triangle is 15 cm long. Thus, P = 3(15) = 45 cm.
Sample Problem 3: A car drove 1200 meters from Main Park to the Heritage Museum. After a 3-hour visit to the museum, the car went another 600 meters from Heritage Museum to the “All Around” Supermarket. Finally, the “All Around” Supermarket car returned to Main Park. Determine the total distance traveled by car throughout its trip, assuming that the distance from Main Park to the Heritage Museum and “All Around” Supermarket to Main Park is equal. Refer to the figure below for the map:
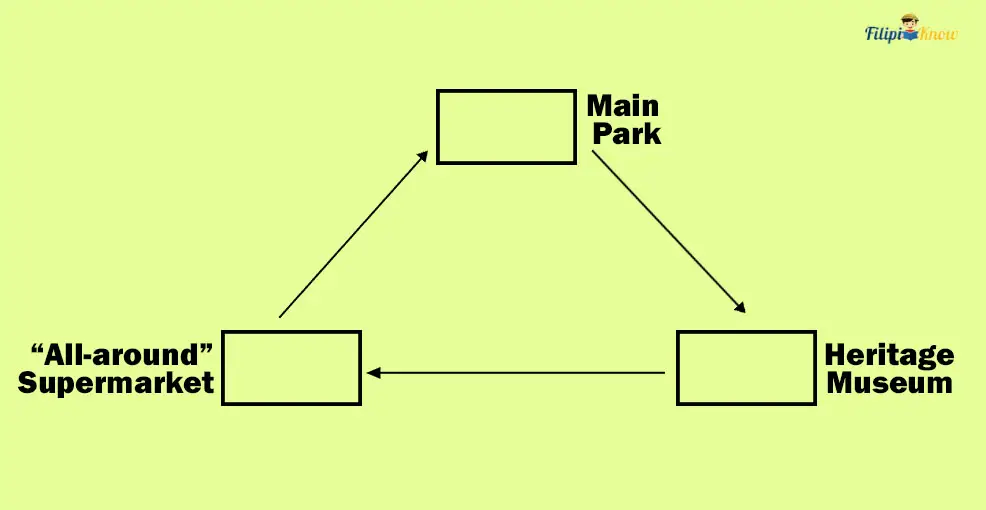
Solution: From the figure above, notice that the entire distance the car covers throughout its trip forms a triangle. Furthermore, since the distance from Main Park to Heritage Museum and “All Around” Supermarket to Main Park are equal, we can conclude that the triangle formed is isosceles.
To find the car’s total distance, we need to compute the perimeter of the isosceles triangle. In an isosceles triangle, two sides are congruent. In our problem, the one with a 1200 m side is congruent to the other side. So, we have two sides with lengths of 1200 m.
Thus, our isosceles triangle above has sides of 1200 m, 1200 m, and 600 m:
To find the perimeter of the triangle, let us add these sides:
P = a + b + c = 1200 + 1200 + 600 = 3000 m
Hence, the perimeter of the triangle formed by Main Park, Heritage Museum, and “All Around” Supermarket is 3000 m. Therefore, the car covered 3000 m throughout its trip.
Perimeter of a Square
A square is a quadrilateral (four-sided polygon) with all four sides congruent. This means that all sides of a square have equal lengths. Furthermore, note that the interior angles of a square are all right angles.
We know that the perimeter of a plane figure is just the sum of the lengths of the side of the plane figure. So, to find the perimeter of a square with side s (given that all of the sides of the square will have a measurement of s), we are just going to add these sides:
Psquare = s + s + s + s
We can rewrite the formula above more concisely:
Psquare = 4s
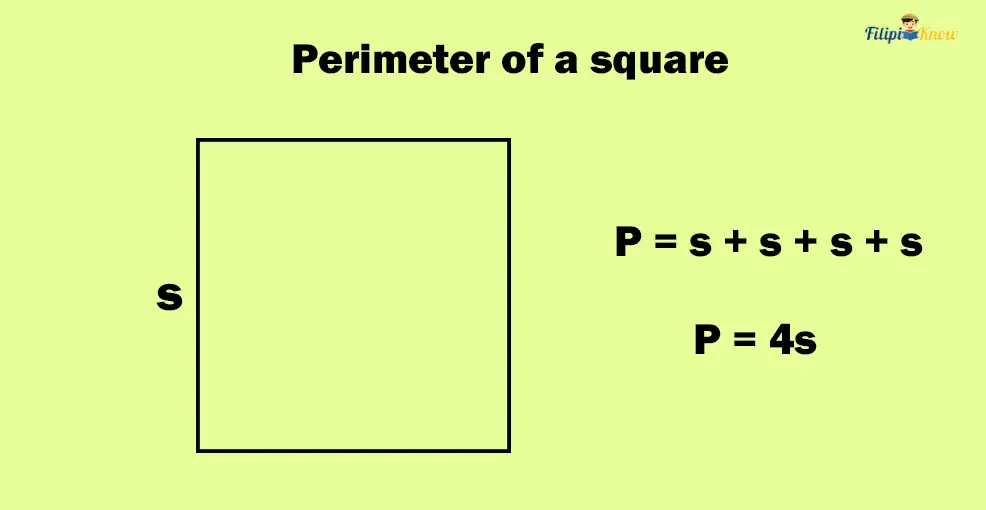
Therefore, the perimeter of a square is just four times the measurement of its side.
Sample Problem 1: A square has a side that measures 10 cm. Determine its perimeter.
Solution: Using the formula for the perimeter of a square: Psquare = 4s = 4(10) = 40 cm
Sample Problem 2: A square piece of wood has sides that are 2 meters long. Suppose that the side lengths of the same piece of wood were reduced by 50%. By how much percent does the perimeter of the square piece of wood change?
Solution: Let us start by calculating the perimeter of the square piece of wood without the 50% reduction of the length of its sides. The original length of the square piece of wood is 2 meters long, so the original perimeter would be calculated as follows:
Using the original length of the sides (s = 2 cm)
Poriginal square = 4s
Poriginal square = 4(2) = 8 m
So, the original perimeter of the square is 8m.
Now, let us consider the 50% reduction of the side lengths of the square. The problem stated that the sides of the square were reduced by 50%. It was given that the sides of the original square are 2 meters. 50% of 2 meters is 1 meter (0.50 x 2 = 1). So, the new sides of the square will be 1 m.
Let us compute the new perimeter of the square piece of wood with sides = 1 meter.
Pnew square = 4s
Pnew square = 4(1) = 4 m
Hence, the new perimeter of the square, after reducing the length of its sides by 50%, is 4 meters.
However, we are not done yet. We are interested in finding the percent change in the perimeter of the square. To find this percent change, we subtract the perimeter of the new square from the perimeter of the original square, divide the result by the perimeter of the original square, and multiply the result by 100:
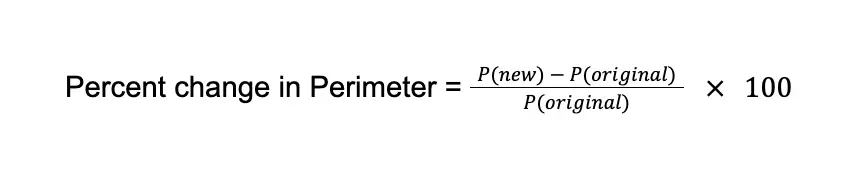
Recall that the perimeter of the original square is 8 meters while the perimeter of the new square is 4 m. Therefore:

The computed percent change in the perimeter is -50%. The negative sign means that the perimeter of the square was reduced by 50%. Hence, the percent change in the perimeter is -50%.
Perimeter of a Rectangle
A rectangle is a quadrilateral (four-sided polygon), where all its interior angles are right angles with opposite sides parallel and congruent.
A rectangle has a pair of equal sides called the length of the rectangle. There is also another pair of equal sides called the width of the rectangle. The length of a rectangle is always longer than its width.
It is important to note that all squares are rectangles, but not all rectangles are squares.
Since the perimeter is just the sum of the sides of a plane figure, then the perimeter of a rectangle is just the sum of its sides or lengths and widths:
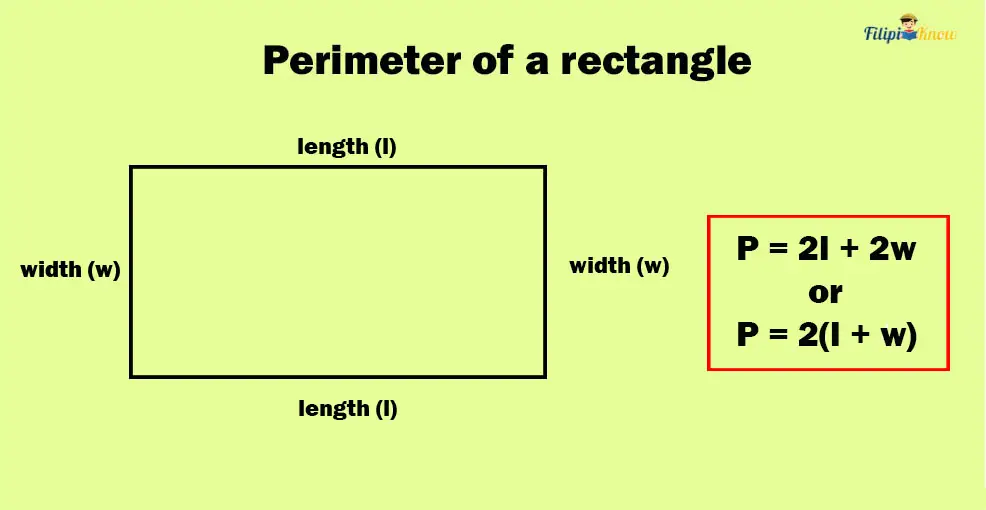
Prectangle = l + l + w + w
We can rewrite the formula above as
Prectangle = 2l + 2w
By the distributive property, we can write the formula above as
Prectangle = 2(l + w)
Sample Problem: A rectangular swimming pool is 45 ft long and 30 ft wide. Determine the perimeter of the swimming pool.
Solution: The length of the rectangular swimming pool is 45 ft, while its width is 30 ft. Hence, we have l = 45 and w = 30.
Let us calculate the perimeter of the rectangle:
P = 2(l + w)
P = 2(45 + 30)
P = 2(75)
P = 150 ft
Perimeter of Other Plane Figures
Generally, to find the perimeter of any plane figure, we have to add the measurements of all of its sides. This means that as long as the measure of all sides of a plane figure is given, you can easily find its perimeter.
Sample Problem 1: A regular hexagon has a side of 120 cm. Determine its perimeter.
Solution: A regular hexagon is a polygon with six sides, all of which are congruent. This means that the given hexagon in this problem has sides that are all 120 cm long. Therefore, we can find the perimeter of the regular hexagon by just adding 120 cm to itself six times or by just multiplying 120 cm by 6:
P = 120(6) = 720 cm
Hence, the perimeter of the hexagon is 720 cm.
Sample Problem 2: The figure below is a trapezoid. Determine its perimeter.
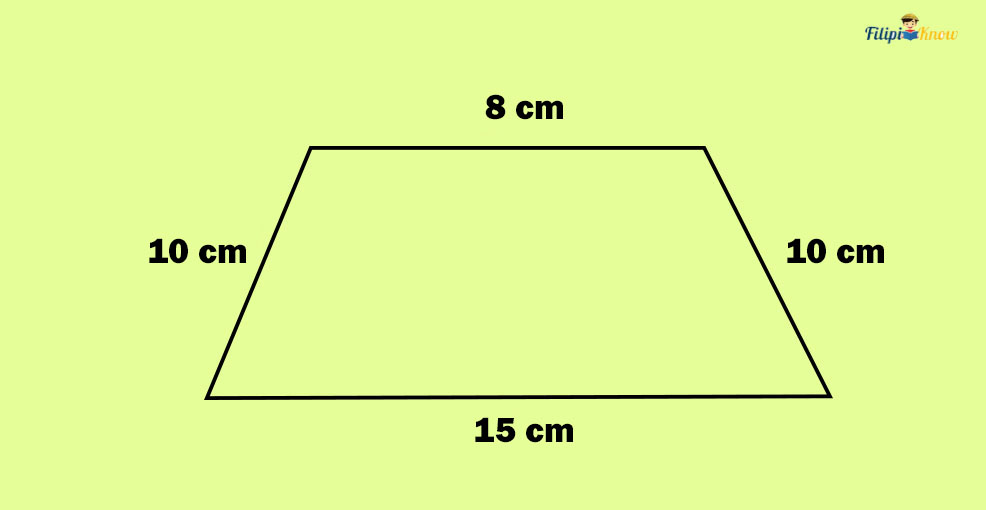
Solution: A trapezoid is a quadrilateral with one pair of parallel and another pair of non-parallel sides. The figure you see above is an example of a trapezoid. Since all of the sides of the trapezoid have indicated measurements, we can determine its perimeter just by simply adding these sides:
P = a + b + c + d
P = 10 cm + 15 cm + 10 cm + 8 cm = 43 cm
The perimeter of the trapezoid is 43 cm.
Sample Problem 3: Identify the perimeter of the given figure below if Triangle PQR is an equilateral triangle and QSVR is a square. The perimeter of Triangle PQR is 27 cm.
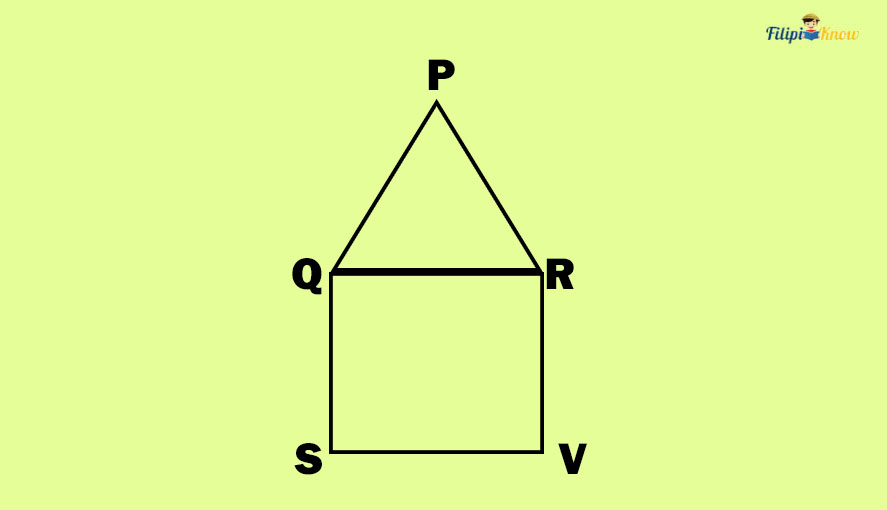
Solution: The figure above has no sides with indicated length or measurement. Does it mean that we cannot find the perimeter of the figure?
No, we can derive the measurement of the sides by analyzing the given figure and the given conditions in the problem.
First, triangle PQR is an equilateral triangle with a perimeter of 27 cm. Hence, a side of the triangle PQR is 27 ÷ 3 = 9 cm long.
This means that the side QR of the triangle is 9 cm long. Note that side QR is not just a side of triangle PQR but also a side of the square QSVR. Hence, all sides of QSVR must be 9 cm also since one of its sides, QR, is already 9 cm long.
Now, we have derived all the measurements of the sides of the given figure:

Hence, to find the perimeter of the figure above, we will add the sides PQ, QS, SV, VR, and RP, which are all 9 cm long. Side QR is omitted since it is not part of the sides surrounding the entire figure.
Perimeter = PQ + QS + SV + VR + RP = 9 + 9 + 9 + 9 + 9 = 45 cm.
Hence, the perimeter of the figure above is 45 cm.
Does a Circle Have a Perimeter?
Like any other plane figure, we can determine the total distance around a circle. However, we do not call this distance “perimeter” since it refers to the sum of the sides of a plane figure (a circle has no sides). Instead, circumference is the name we use to refer to the distance around a circle.
Part II: Area of a Plane Figure
We have learned that the perimeter of a plane figure refers to the total distance around that figure. This time, let us talk about the area of a plane figure.
Area refers to the entire space occupied by a plane figure.
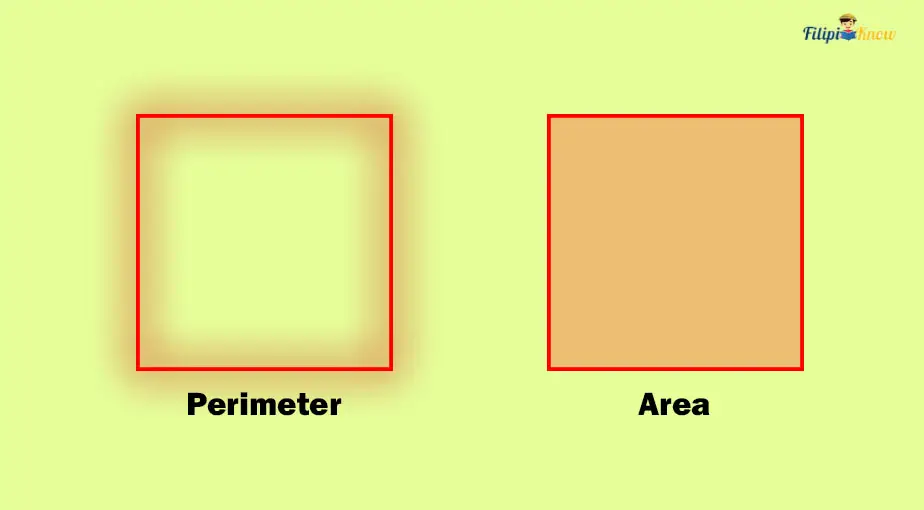
In other words, area refers to the space inside the given plane figure.
Imagine a picture frame with a picture inside it. You can think of the frame as the perimeter, while the space occupied by the picture inside the frame is the area.
We use square units to determine this “amount of space” inside a plane figure. In the figure below, the rectangle has 30 square units (try manually counting the square units inside the rectangle). Hence, the “amount of space” occupied by the rectangle below is 30 square units. The area of the rectangle is 30 square units.

Summary of Formulas for the Area of Plane Figures
Counting the number of square units inside a plane figure is a great way to find its area. However, plane figures in the real world will not appear with square units inside them. For this reason, we have to use formulas derived by mathematicians and geometers throughout the centuries to determine the area of a plane figure. These formulas are what we are going to discuss in the succeeding sections.
| Plane Figure | Formula for Area |
| Triangle | A = ½ bh where b and h are the base and height of the triangle If equilateral triangle: A = s²(√3/4) where s is a side of the equilateral triangle |
| Square | A = s2 where s is a side of the square |
| Rectangle | A = l x w where l and w are the length and width of the rectangle, respectively |
| Parallelogram | A = b x h where b and h are the base and height of the parallelogram |
| Trapezoid | A = ½ (b1 + b2)h where b1 and b2 are the bases of the trapezoid and h is the height |
| Rhombus | A = ½ (d1d2) where d1 and d2 are the diagonals of the rhombus |
Let’s now discuss these formulas one by one.
Area of a Triangle
The formula below gives the area of a triangle:
Atriangle = ½ (b x h)
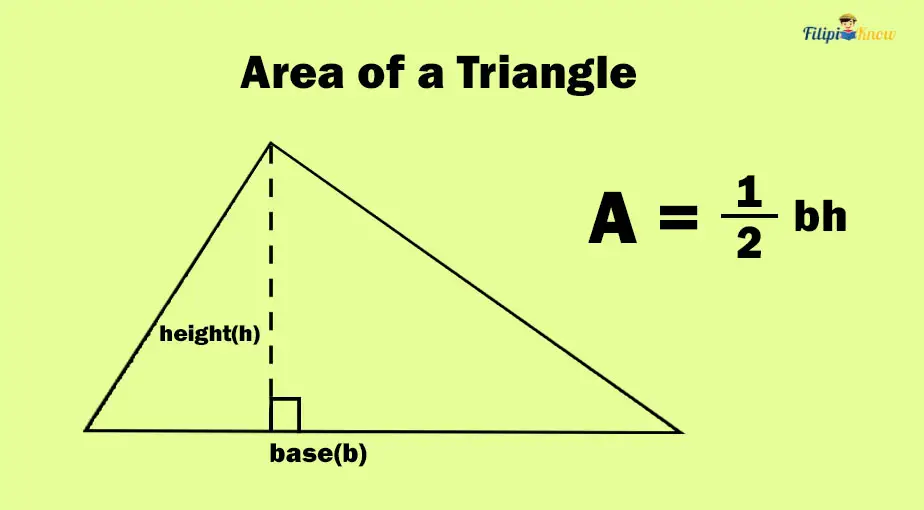
Where b is the triangle’s base, and h is the triangle’s height. The triangle’s height is the distance from the base to the vertex of the triangle opposite the base. Note that the base and the height of the triangle are perpendicular.
The formula above tells us that the area of a triangle is equal to half of the product of its base and height.
Sample Problem 1: Compute the area of the triangle below.
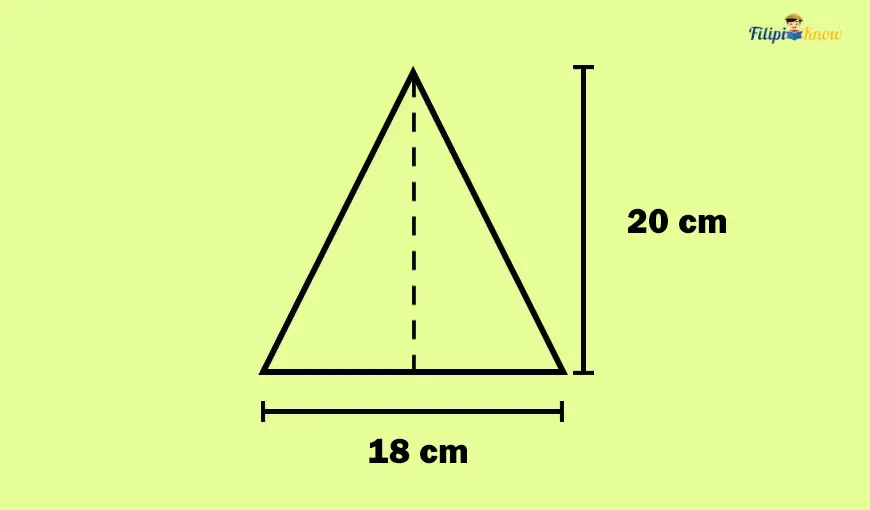
Solution: The height of the given triangle is 20 cm, while its base is 18 cm. So, we have h = 20 and b = 18. Using the formula for the area of a triangle:
A = ½ (b x h)
A = ½ (18 x 20)
A = 180
Thus, the area of the triangle is 180 cm2.
Note that a plane figure’s area is always given in square units. This means that if the dimensions of a plane figure are in centimeters (cm), then the area of the plane figure must be in square centimeters (cm2). Likewise, if the dimensions of a plane figure are in feet (ft), then its area must be given in square feet (ft2).
If a triangle is equilateral (all sides are congruent), we can determine its area using only one of its sides. The formula for the area of an equilateral triangle given one of its sides is defined by the “not so” complex formula below:

Unfortunately, the only way to remember this formula for the area of an equilateral triangle is by just memorizing it unless you can derive it using deductive reasoning (which is beyond the scope of this reviewer).
In the formula above, s represents the side of the equilateral triangle. Hence, the area of an equilateral triangle is the square of its side times the square root of three over four.
Sample Problem 2: The side of an equilateral triangle is 4 cm long. Determine its area.
Solution: Since the given triangle is equilateral and one of its sides has a measurement, we can use the formula above for the area of an equilateral triangle.
We have s = 4. By substitution:
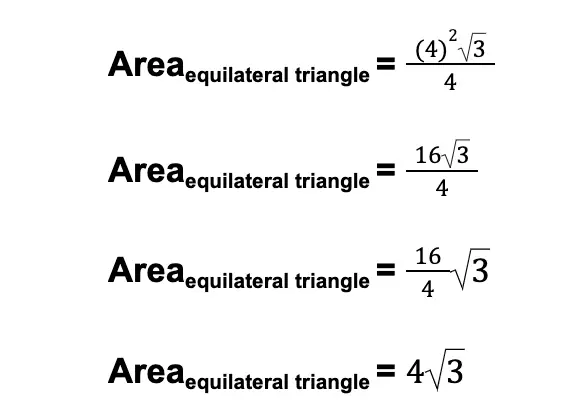
Therefore, the area of the equilateral triangle in the problem is 4√3 cm2.
Area of a Square
The area of a square is just the measurement of its side raised to the power of 2 (or square of the side).
Asquare = s2

Sample Problem 1: A square has a side that measures 2.5 cm. Determine its area.
Solution: Using the formula for the area of a square:
Asquare = s2
Asquare = (2.5)2
Asquare = 2. 5 x 2.5 (recall that a2 = a x a)
Asquare = 6.25
Therefore, the area of the square is 6.25 cm2.
Sample Problem 2: The perimeter of a square is 20 cm. Determine its area.
Solution: From the given perimeter of the square, we can derive its side. Recall that the formula P = 4s gives the perimeter of a square.
The perimeter of the square is 20 cm. Let us find the measurement of its side:
P = 4s
20 = 4s
4s = 20 Symmetric property of equality
4s⁄4 = 20⁄4 Dividing both sides of the equation by 4
s = 5
Thus, a side of the square measures 5 cm.
Now that we know one of its sides, we can determine the area of the square:
A = s2
A = (5)2
A = 25
Thus, the area of the square is 25 cm².
Area of a Rectangle
The area of a rectangle is just the product of its length (l) and width (w).
A = l x w
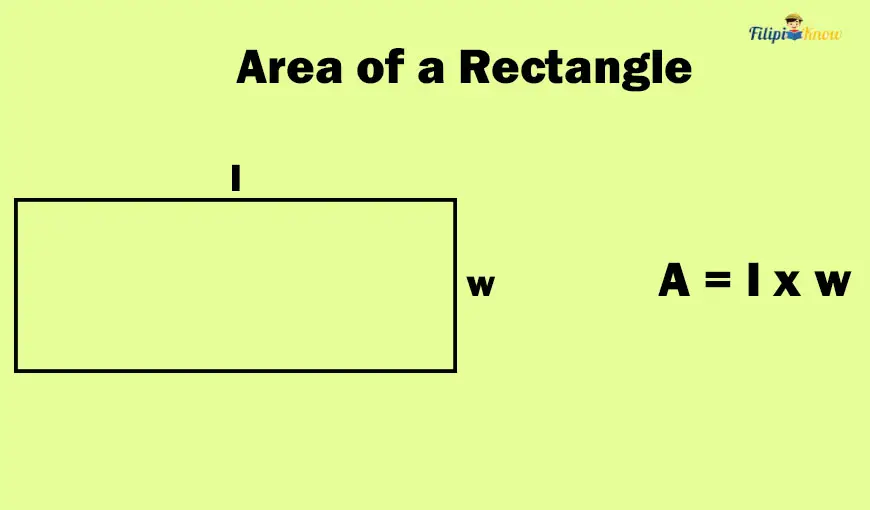
Sample Problem 1: A rectangular garden is 15 meters long and 12 meters wide. Calculate the area covered by the rectangular garden.
Solution: Since the garden is rectangular, we can multiply its length and its width to determine its area:
A = 15 x 12
A = 180
Hence, the area of the rectangular garden is 180 square meters (m2).
Sample Problem 2: Mang Pedring plans to sell his lot in the village. The length of his lot is about 15 meters, and its width is about 12.5 meters. He plans to sell his lot for about ₱1500 for every square meter. If Mang Pedring successfully sold his lot, how much would he probably receive?
Solution: The pricing of the lot depends on how many square meters it occupies. Thus, to determine the amount of money Mang Pedring might receive from successfully selling it, we must first determine the area of the lot.
We are given the length and width of the lot. This means that we can compute its area using the formula for the area of a rectangle:
A = l x w
We have l = 15 and w = 12.5
A = 15 x 12.5
A = 187.5
Hence, Mang Pedring’s lot has an area of 187.5 square meters (m2).
Recall that each square kilometer of the lot will cost ₱1500, so a 187.5 square kilometer lot will cost:
1500 x 187.5 = ₱281,250
Hence, Mang Pedring will receive ₱281,250 if he successfully sells his lot.
Area of a Parallelogram
A parallelogram is a quadrilateral with two pairs of parallel sides.
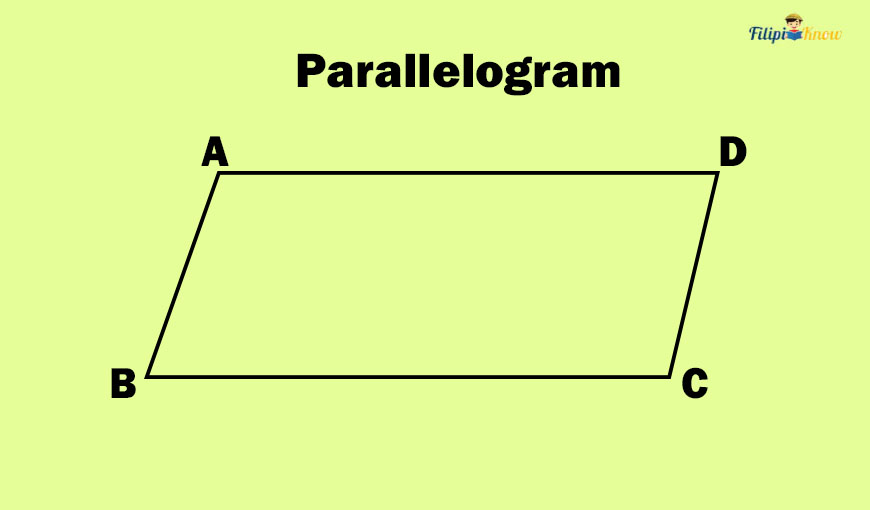
In the figure above, ABCD is a parallelogram since it is four-sided and has two pairs of parallel sides (AD || BC and AB || CD).
What is the difference between a parallelogram and a rectangle?
A rectangle is a parallelogram since it has four sides and two pairs of parallel sides. However, a rectangle has four right angles as interior angles, while in a parallelogram, the interior angles cannot be right angles.
This means that all rectangles are parallelograms, but not all parallelograms are rectangles.
Anyway, the image above provides a visual illustration of how the parallelogram looks and how it differs from a rectangle.
The area of a parallelogram is the product of its base and its height:
Aparallelogram = b x h
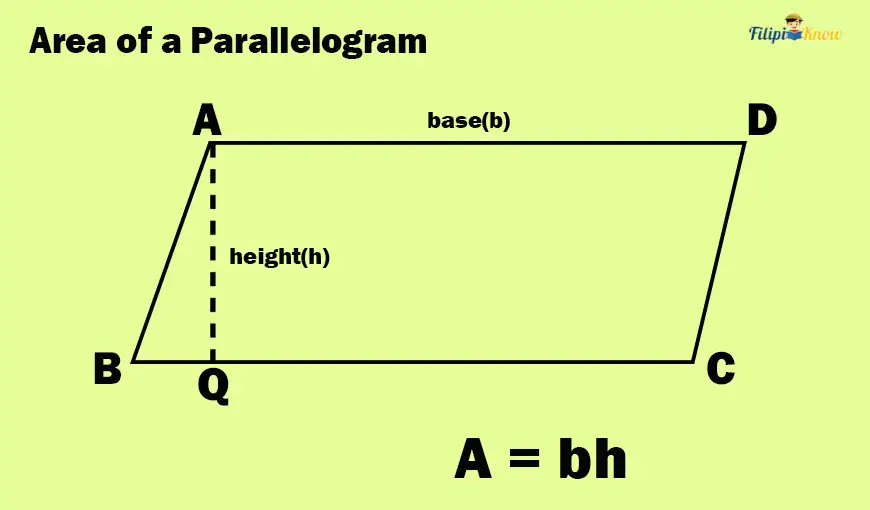
The base of the parallelogram can be any of its sides. Meanwhile, its height is the vertical distance from its base to the side parallel to the base.
In the figure above, we use BC as the base of the parallelogram. Line segment AQ is its height since it is the vertical distance from the base BC to the side parallel to BC, which is AD (recall that AD || BC).
Sample Problem 1: Determine the area of the parallelogram below:
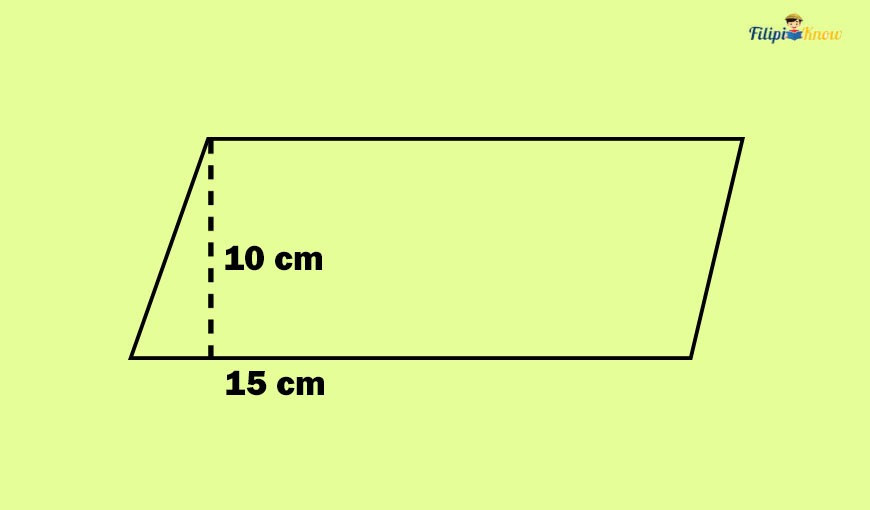
Solution: The base of the parallelogram is 15 cm long, while its height is 10 cm long. The area of a parallelogram is simply the product of its base and height. Therefore,
A = b x h
A = 15 x 10
A = 150 cm2
The area of the parallelogram is 150 cm2.
Area of a Trapezoid
A trapezoid is a quadrilateral with one pair of sides parallel and one pair of sides that are not parallel.
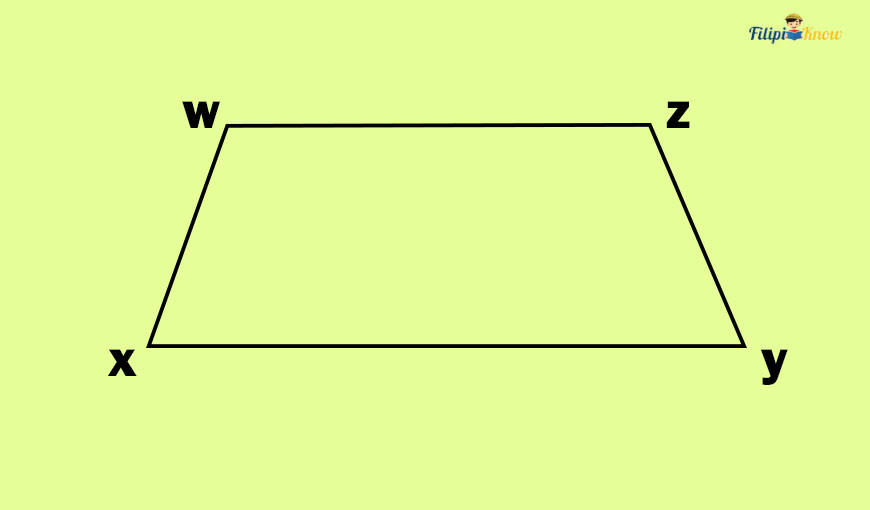
Quadrilateral WXYZ is a trapezoid since it has one pair of parallel sides (WZ || XY) and one pair of non-parallel sides (WX and YZ are not parallel because when you extend both of these sides, they will intersect).
The parallel sides of the trapezoid are called the bases of the trapezoid. Thus, a trapezoid has two bases. The vertical distance from one base to another is called the height of the trapezoid.
In our figure above, WZ and XY are the bases of the trapezoid since they are parallel sides. If you draw a vertical line connecting WZ and XY, you will have the height of the trapezoid.
The area of a trapezoid is equal to half the product of the sum of the bases and the height. We state it mathematically in the formula below.
Atrapezoid = ½ (b1 + b2)h
Where b1 and b2 are the bases or the parallel sides of the trapezoid, and h is the height or the vertical distance between these bases.
Sample Problem: Calculate the area of the trapezoid PQRS below.
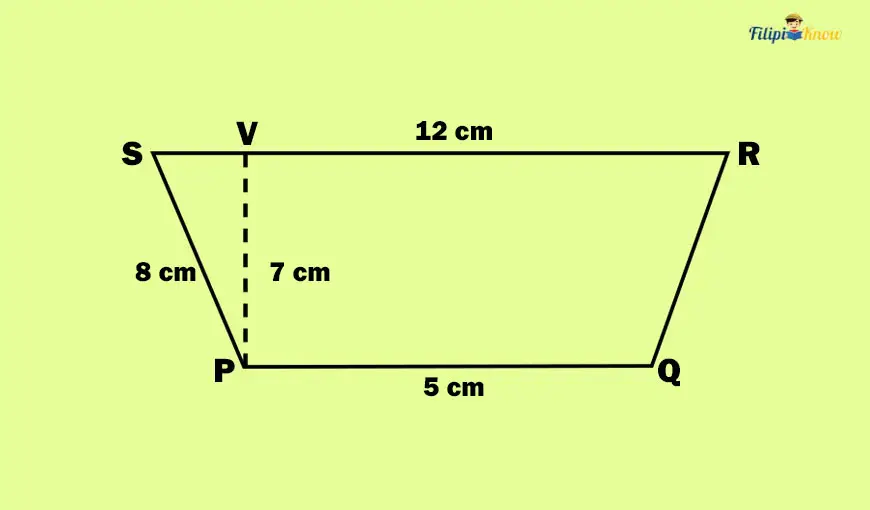
Solution: The bases of the trapezoid above are PQ and RS. Meanwhile, the line segment PV is the height. Side PS with a measurement of 8 cm is irrelevant to this problem.
So we have b1 = 5 cm, b2 = 12 cm, and h = 7 cm.
Using the formula for the area of a trapezoid:
A = ½ (b1 + b2)h
A = ½ (5 + 12)7
A = ½ (17)7
A = 59.5
Thus, the area of the trapezoid PQRS is 59.5 cm2.
Area of a Rhombus
So far, we have learned how to find the areas of some common quadrilaterals, such as squares, rectangles, parallelograms, and trapezoids. Now, let us discuss how to find the area of a rhombus which is also a common quadrilateral.
A rhombus is a quadrilateral with all sides congruent. I know you will ask how a rhombus is different from a square. Here’s the difference – a square is a quadrilateral with all sides congruent, and all interior angles are right angles. However, a rhombus is a quadrilateral with all sides congruent, and its interior angles can be acute or obtuse.
In a square, the sides are perpendicular since they form right angles, but in a rhombus, the sides may not be perpendicular since interior angles can be acute or obtuse.
In the image below, you can see Square ABCD and rhombus DEFG. Can you spot their differences?

To determine the area of a rhombus, we do not use its sides. Instead, we use its so-called diagonals.
A diagonal is a line segment that connects two opposite vertices of a polygon. Take note that the vertices of a polygon are its corners where the sides meet. Hence, the diagonal connects two opposite corners of a polygon.
Take a look at rhombus DEFG. E and G are opposite corners of the rhombus. If we connect these corners, we form the line segment EG. Segment EG is a diagonal of rhombus DEFG.
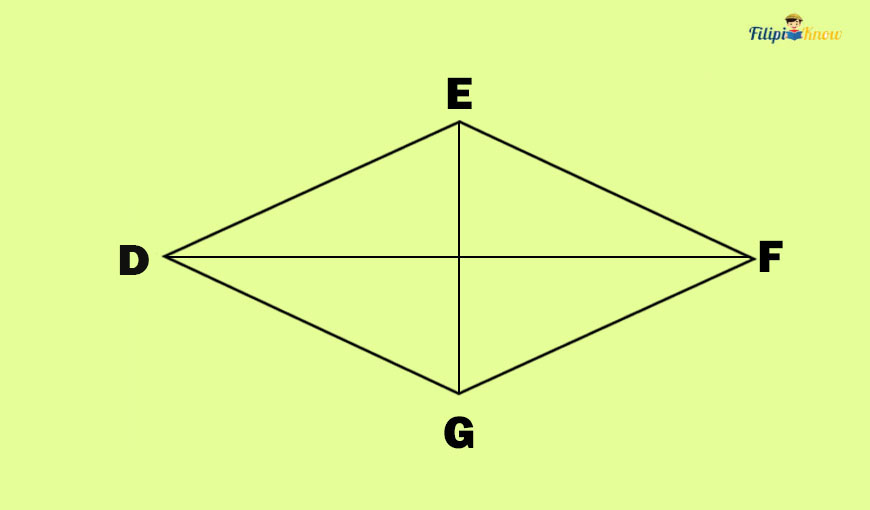
Same as with E and G, D and F are opposite corners of rhombus DEFG. We will form the line segment DF if we connect D and F. Therefore, segment DF is a diagonal of rhombus DEFG.
If you have the measurements of the diagonals of a rhombus, you can determine its area. The formula for the area of a rhombus given its diagonals is:
Arhombus = ½ (d1 x d2)
Where d1 and d2 are the measurements of the diagonals of the rhombus.
Sample Problem: What is the area of the rhombus below?
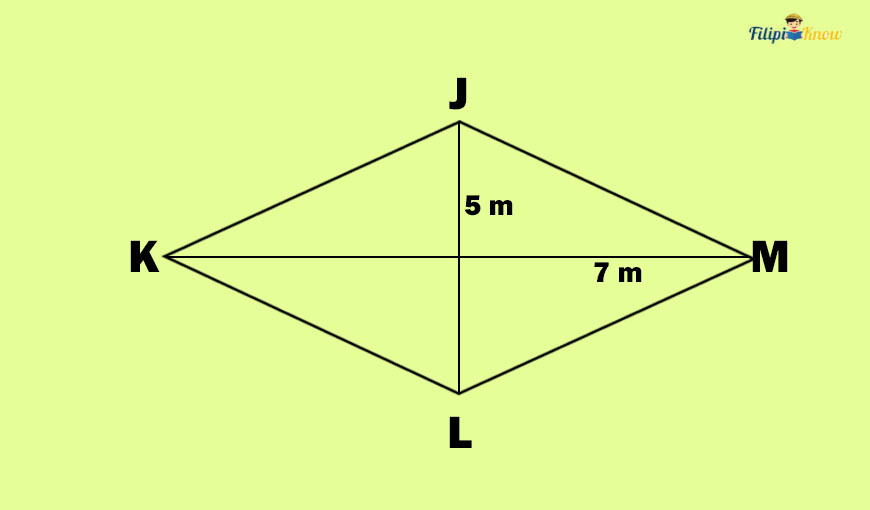
Solution: We have the measurements of the diagonals of rhombus JKLM. In particular, we have JL = 5 meters and KM = 7 meters. So we have d1 = 5 and d2 = 7. To find the area of the rhombus, we can just use the formula above:
Arhombus = ½ (d1 x d2)
Arhombus = ½ (5 x 7)
Arhombus = ½ (35)
Arhombus = 17.5
Hence, the area of the rhombus is 17.5 square meters.
Applying the Concepts of Perimeter and Area
Now that you have learned how to compute several plane figures’ perimeter and area, you are ready to solve some more complicated problems involving them. Make sure you know which formula must be used to determine the perimeter or area of a plane figure to ensure that you will accurately obtain the answer.
Sample Problem 1: Main Park is rectangular. The Local Government Unit that manages the Main Park reported that its perimeter is 200 ft, and its width is 40 ft. Can you determine how long the Main Park is?
Solution: It was reported that the perimeter of Main Park is 200 ft, and its width is 40 ft. We also know that Main Park is rectangular. The formula for the perimeter of a rectangle is given by:
P = 2l + 2w
Since the Main Park has a perimeter of 200 ft and a width of 40 ft:
200 = 2l + 2(40)
To find the length of Main Park, we must solve for the value of l in the equation above:
200 = 2l + 2(40)
200 = 2l + 80 Simplifying the equation
2l + 80 = 200 Symmetric property of equality
2l = -80 + 200 Transposition method
2l = 120
2l⁄2 = 120⁄2
L = 60
The computed value of l is 60. Since l represents the length of Main Park, then the Main Park is 60 ft long.
Sample Problem 2: Marvin plans to cut some 25 cm2 squares out of cartolina paper with a length of 25 cm and a width of 20 cm. How many squares can Marvin cut from the cartolina paper?
Solution: The number of squares Marvin can cut from the cartolina paper depends on how many 25 cm2 squares fit inside it. Thus, we need to find the area of the cartolina paper first before we’ll be able to determine how many 25 cm2 squares can fit into it.
We are given the length and the width of the cartolina paper, which are 25 cm and 20 cm, respectively. Thus, we can use the formula for the area of a rectangle:
Arectangle = l x w
We have l = 25 and w = 20:
A = 25 x 20
A = 500
Hence, the area of the cartolina paper is 500 cm2.
Our next step is to find how many 25 cm2 squares can fit inside this cartolina paper, which we have discovered has an area of 500 cm2. We can determine this by dividing the area of the cartolina paper (which is 500 cm2) by 25 cm2:
Number of 25 cm² that can be cut = 500 ÷ 25 = 20
Thus, Marvin can cut twenty (20) 25 cm2 squares from the cartolina paper.
Sample Problem 3: Suppose that the length of the sides of the square was doubled. What will happen to the area of the square?
Solution: We can solve this problem using two methods.
Method 1:
The problem didn’t provide us with any measurement of the sides of the square. Hence, we will assume an arbitrary value for the side.
Let’s say the side of that square is 10 cm.
The area of a square with 10 cm side is A = s2 = (10)2 = 100 cm
Now, if we double the side of the square from 10 cm to 20 cm, the new area will be A = s2 = (20)2 = 400.
So, what have you noticed?
The area of the original square quadrupled (increased by four times) from 100 cm to 400 cm.
Hence, if we double the sides of a square, its area will quadruple (increased by four times).
Method 2:
Recall that the area of a square is A = s2 such that s is the length of a side of the square.
If we double the side of the square, then its size will be 2 x s = 2s.
Hence, the new area of the square will be A = s2 = (2s)2 = 4s2
So, the old area of the square is A = s2, and its new area is now A = 4s2. What have you noticed?
Yes, the area of the square quadrupled (increased by four times) after we doubled the length of its side.
Next topic: Volume of Solid Figures
Previous topic: Conversion of Units of Measurement
Return to the main article: The Ultimate Basic Math Reviewer
Download Printable Summary/Review Notes
Download Printable Flashcards
Test Yourself!
1. Practice Questions [Free PDF Download]
2. Answer Key [Free PDF Download]
3. Math Mock Exam + Answer Key
Written by Jewel Kyle Fabula
in Civil Service Exam, College Entrance Exam, LET, NAPOLCOM Exam, NMAT, PMA Entrance Exam, Reviewers, UPCAT
Jewel Kyle Fabula
Jewel Kyle Fabula graduated Cum Laude with a degree of Bachelor of Science in Economics from the University of the Philippines Diliman. He is also a nominee for the 2023 Gerardo Sicat Award for Best Undergraduate Thesis in Economics. He is currently a freelance content writer with writing experience related to technology, artificial intelligence, ergonomic products, and education. Kyle loves cats, mathematics, playing video games, and listening to music.
Copyright Notice
All materials contained on this site are protected by the Republic of the Philippines copyright law and may not be reproduced, distributed, transmitted, displayed, published, or broadcast without the prior written permission of filipiknow.net or in the case of third party materials, the owner of that content. You may not alter or remove any trademark, copyright, or other notice from copies of the content. Be warned that we have already reported and helped terminate several websites and YouTube channels for blatantly stealing our content. If you wish to use filipiknow.net content for commercial purposes, such as for content syndication, etc., please contact us at legal(at)filipiknow(dot)net
