How To Solve Geometry Problems Involving Angles

Have you ever used a protractor?

If we want to draw an angle, we need a protractor and use it as a guide. Through the protractor, we can visually depict the concept of angles. 

But what exactly is an angle? Why do we have to draw them using protractors? What is their practical significance?

Angles are of particular importance in the study of geometry. They possess potent characteristics that enable us to understand geometric figures better. 

In this module, you will learn everything you must remember about angles, including their definition, classification, and properties.

Click below to go to the main reviewers:

Ultimate UPCAT Reviewer

Ultimate PMA Entrance Exam Reviewer

Ultimate NAPOLCOM Exam Reviewer

Ultimate LET Reviewer

What Is an Angle?

An angle consists of two rays that have the same endpoint. The endpoint where the rays intersect is called the vertex. Meanwhile, the rays are called the sides.

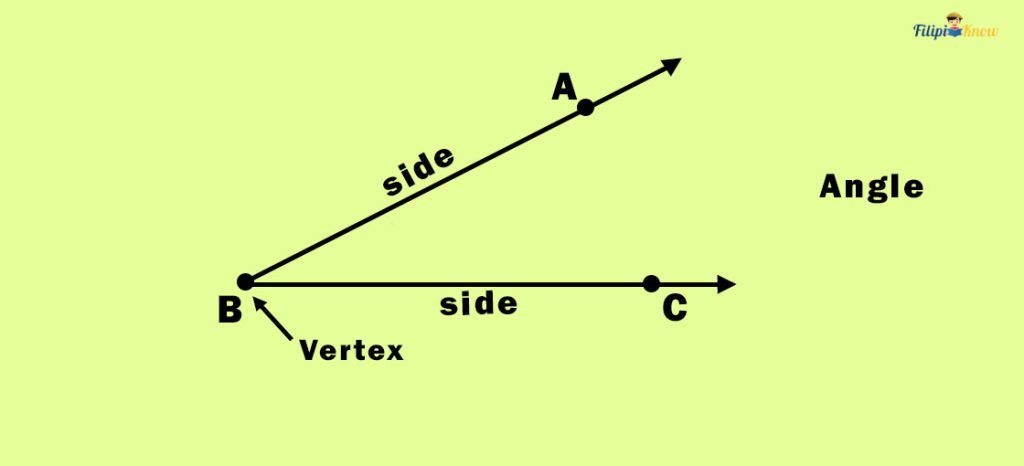
We use the points of the sides of the angles to name the angle. In the figure above, we call the angle ∠ABC where B is the angle’s vertex (since it is the common endpoint of the rays). We can also name the angle ∠CBA. 

Note that we must put the letter representing the vertex in the middle when naming an angle. 

Be careful when naming an angle. In the figure above, we can call it ∠ABC or ∠CBA but not ∠BAC or ∠CAB since the vertex (point B) must always be in the middle of the angle’s name.  

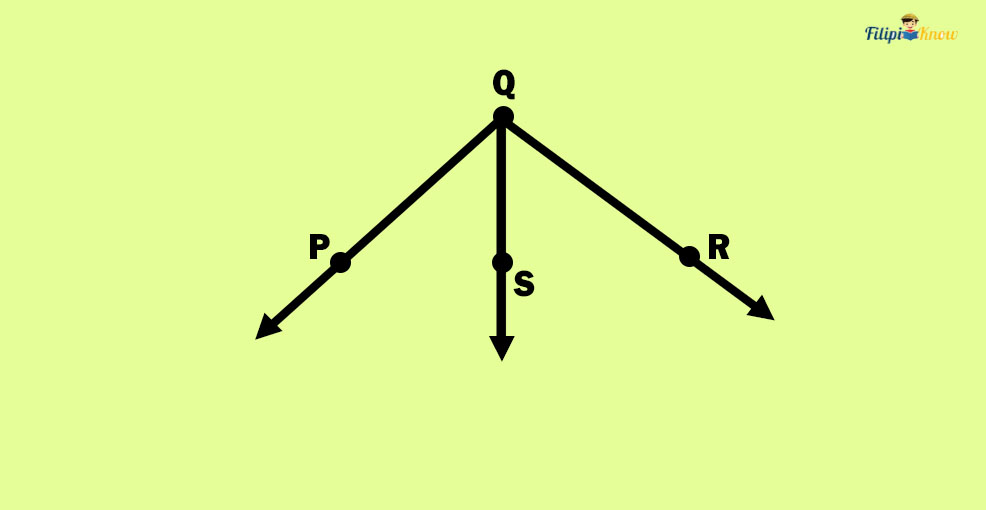
Sample Problem 1: Determine the angles you can see in the given figure below.

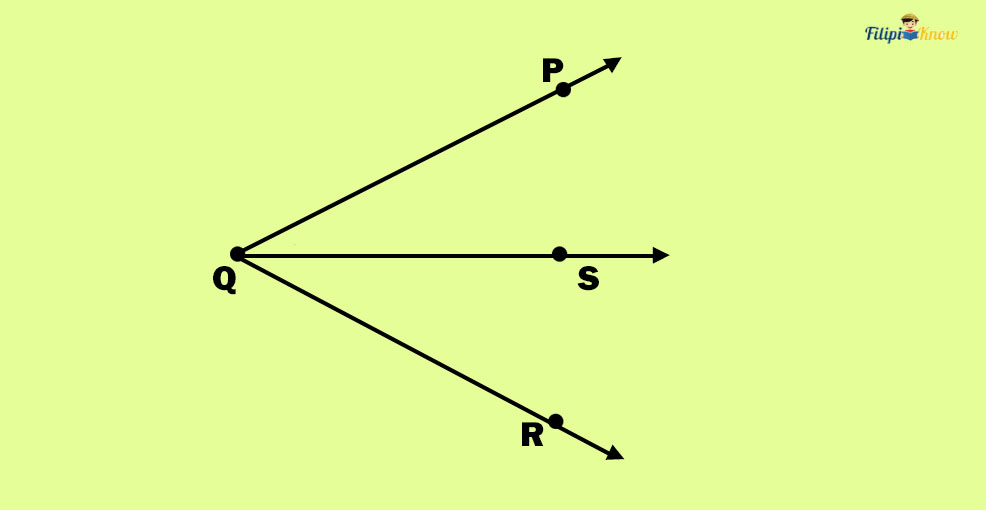
Answer: The angles are ∠PQR, ∠PQS, and ∠SQR.

Sample Problem 2: Using the exact figure above, is SRQ an angle?

Answer: No, because there are no two rays with R as their common endpoint.

Angle Measurement

Just like any geometric figure, we can also measure an angle.

To understand the “measurement of an angle,” we must learn the Protractor Postulate.

Protractor Postulate

“The measurement of an angle refers to the measurement between two rays which  can be designated as a real number from 0 to 180 degrees.”

The protractor postulate assumes that every angle can measure 0 to 180 degrees. Degrees (°) is the unit of measure we use for angles.

How exactly do we measure an angle?

We measure an angle using a protractor. Suppose a protractor was placed against the angle ∠ABC below. We put the ABC vertex in the protractor’s lower middle part. It is clearly seen that ray AB is pointed to 120° while point BC is pointed to 0°. The measurement of ∠ABC is the absolute value of the difference between the numbers the rays are pointed to. Thus, the measure of ∠ABC is 120°

It’s nice to learn how to measure angles using protractors. However, since you are preparing for a college entrance exam (or civil service exam), it is most likely that the measurement of the angles is already given in the questions, so you don’t have to use a protractor to determine the measure of an angle. We just have provided you with an idea of the measurement of the angle. 

We use the symbol m∠ABC to refer to the measurement of angle ∠ABC. Hence, if ∠ABC measures 120°, then m∠ABC = 120°.

Classification of Angles

We can classify angles according to their measurement. An angle can be an acute angle, a right angle, an obtuse angle, or a straight angle.

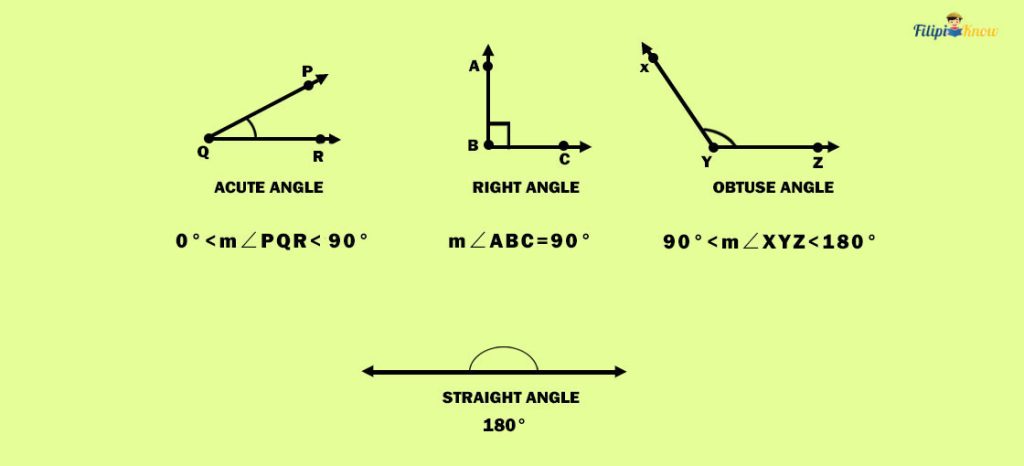
1. Acute Angle

An acute angle is an angle whose measure is between 0° and 90°.

For instance, if m∠PQR = 45°, ∠PQR is an acute angle.

2. Right Angle

A right angle is an angle whose measure is exactly  90°. Notice how the right angle looks like the letter “L.” 

Take note of the word “exactly” in the definition of right angles. The term “exactly” implies that the measure of a right angle must be strictly 90 degrees. If the angle measure is 90.5°, we cannot consider it a right angle.

3. Obtuse Angle

An obtuse angle is an angle whose measure is between 90° to 180°.

For instance, if m∠XYZ = 105°, ∠XYZ is an obtuse angle.

4. Straight Angle

If an angle has a measurement of exactly 180°, we call that angle a straight angle (which is a straight line).

Sample Problem 1: Determine if the following angles are acute, right, obtuse, or straight.

1. m∠ABC = 125°
2. m∠COR = 90.5°
3. m∠RAW = 0.01°
4. m∠CDO = 179.12°

Answer:

1. Obtuse, since 125 is between 90 to 180
2. Obtuse, since 90.5 is between 90 to 180 (the angle is not a right angle)
3. Acute, since 0.01 is between 0 to 90
4. Obtuse, since 179.12 is between 90 to 180

Sample Problem 2: What type of angle is formed by the hands of the clock when it’s three o’clock?

Answer: It is evident that the angle formed by the hands of the clock at three o’clock is a 90° angle since it resembles the letter “L.” Thus, the angle formed is a right angle.

Sample Problem 3: What type of angle is formed by the hands of the clock when it’s two o’clock?

Answer: When the hands of the clock are at three o’clock, they form a right triangle. Since the angle formed when it’s two o’clock is shorter than the angle formed when it’s three o’clock, the angle must be an acute angle.

Angle Addition Postulate

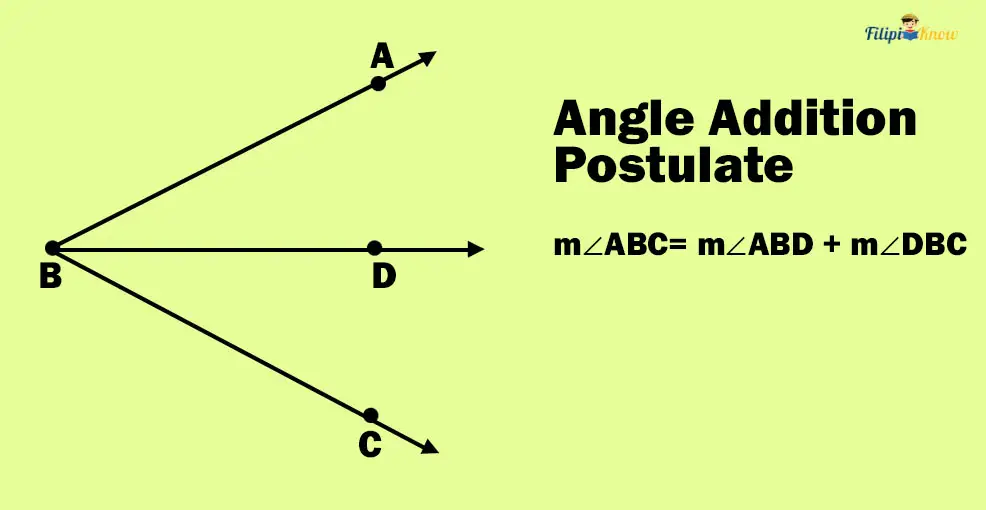
“If D is in the interior of ∠ABC, then the measure of ∠ABC is equal to the sum of the measures of ∠ABD and ∠DBC”

In symbols, m∠ABC = m∠ABD + m∠DBC

The angle addition postulate is very intuitive and self-explanatory. The concept of the angle addition postulate is analogous to the idea of the segment addition postulate discussed previously. To find the measure of the entire angle ∠ABC in the figure above, we can just add the angles that composed it, which are ∠ABD and ∠DBC.

Sample Problem 1: If ∠PQR = 25, ∠PQS = 3x + 10, and ∠SQR = 2x, determine the value of x.

Solution: 

The angle addition postulate tells us that the measure of the entire angle ∠PQR is equal to the sum of the measurements of the angles it contains ( ∠PQS and ∠SQR).

Hence: m∠PQR = m∠PQS + m∠SQR

Using the values given in the problem:

m∠PQR = m∠PQS + m∠SQR

25 = (3x + 10) + 2x

We can now solve the value of x in the given equation above:

25 = (3x + 10) + 2x

25 = 5x + 10 Combining like terms

-10 + 25 = 5x Transposition method

15 = 5x

15/5 = 5x/5 Dividing both sides by 5

3 = x

x = 3 Symmetric property of equality

Thus, the value of x must be 3. 

Sample Problem 2: Using the figure below, determine the measure of ∠ABD.

Solution:

The only given value is the measure of ∠DBC, which is 52 degrees. 

Notice that the angles ∠ABD and ∠DBC form a straight angle ∠ABC. We know that a straight angle has a measure of 180 degrees. Therefore, using the angle addition postulate:

m∠ABC = m∠ABD + m∠DBC

Since ∠ABC  is a straight angle:

180 = m∠ABD + m∠DBC

Using the given value of m∠DBC which is 52:

180 =   m∠ABD + 52

Solving for the equation above:

-52 + 180 = m∠ABD 

128 = m∠ABD 

m∠ABD  = 128

Thus, the measure of ∠ABD is 128°.

Congruent Angles

Angles are congruent if they have the exact measurement. This means that congruent angles have the same form and size. 

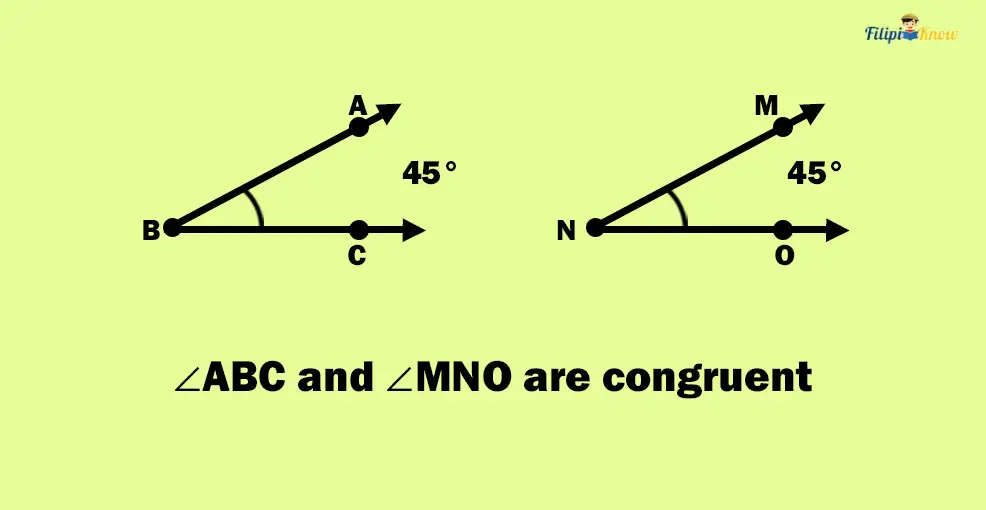
Do you still remember one of Euclid’s postulates that states that all right angles are congruent?

It is pretty apparent why the postulate is true. We defined earlier that right angles have a degree measure that is exactly 90°. Thus, all right angles you create will always have a degree measurement of 90°. Hence, concluding that all right angles are congruent is logically sound. 

Angle Bisector

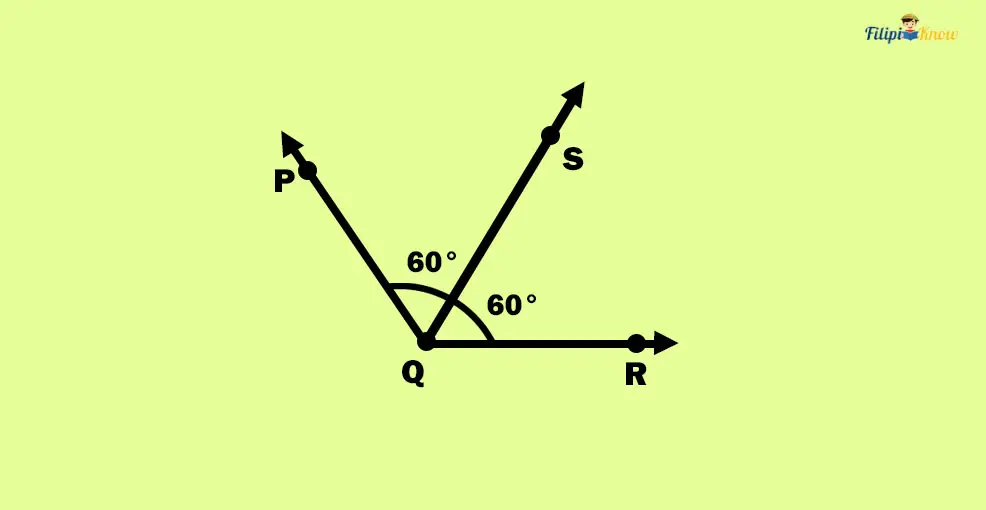
In the figure above, ray QS divides ∠PQR into two congruent angles: PQS and ∠SQR. Ray QS is an example of an angle bisector.

An angle bisector is a ray that divides an angle into two congruent angles.

Sample Problem: In the figure below, ∠MNO is 60°. If ray PN bisects angle ∠MNO, what is the measure of ∠ONP?

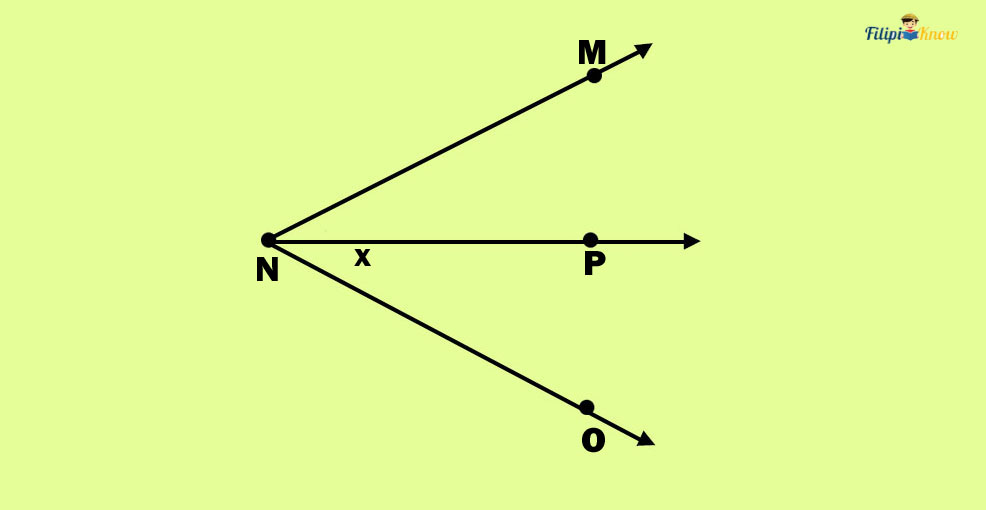
Solution: 

Method 1

Since ray PN bisects ∠MNO, we can conclude that ∠MNO is divided into congruent angles, ∠MNP and ∠ONP. This implies that the measurement of angles ∠MNP and ∠ONP are equal. 

Since the angles ∠MNP and ∠ONP have equal measurements, we can determine the measurement of ∠ONP by dividing the measurement of ∠MNO (60 degrees) by 2.

60 ÷ 2 = 30

Thus, m∠ONP is 30 degrees.

Method 2

Let x represent the measure of ∠ONP. 

Since ray PN bisects ∠MNO, then ∠ONP and ∠MNP have equal measures.

Thus, the measure of ∠MNP is also x

By the angle addition postulates:

m∠ONP + m∠MNP = m∠MNO

x + x = 60 Recall that we let x be the measure of angles ∠ONP and ∠MNP

2x = 60

2x∕2 = 60/2 Dividing both sides by 2

x = 30

Since x represents the measure of ∠ONP, then m∠ONP = 30°.

Angle Pairs

As the name suggests, an angle pair consists of two angles that are related in a certain way. In this section, let us discuss each of these angle pairs.

1. Vertical Angles

Vertical angles are formed when two lines intersect. Vertical angles create two pairs of opposite rays.

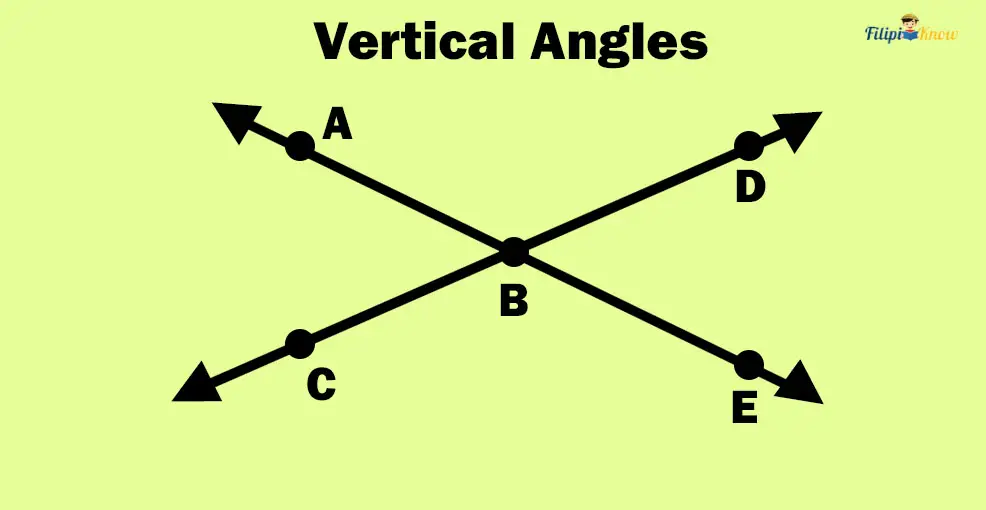
In the given figure above, ∠ABC and ∠DBE are vertical angles. Notice that this angle pair has two pairs of opposite rays: AB and BC (pair 1) and DB and BE (pair 2).

 ∠ABD and ∠CBE are also vertical angles (Can you identify the opposite pair of rays?).

However, ∠ABC and ∠ABD are not vertical angles since they do not form two pairs of opposite rays.

Here’s an “informal” way to detect vertical angles quicker. You can imagine the vertical angles as the opposite openings of the letter “X.” For instance, in the figure above, we can imagine the figure above as the letter X. Notice that angles ∠ABC and ∠DBE are opposite openings of this letter “X,” so they are opposite angles. Same as with ∠ABD and ∠CBE; these angles are also opposite since they are opposite openings of the letter “X.”

Sometimes, vertical angles are also called opposite angles.

Here’s an essential property of vertical angles that you must always keep in mind:

Vertical Angle Theorem

“Vertical angles formed by intersecting lines are always congruent.”

This means that any vertical angle will always have equal degree measurement. 

Retake a look at our previous image:

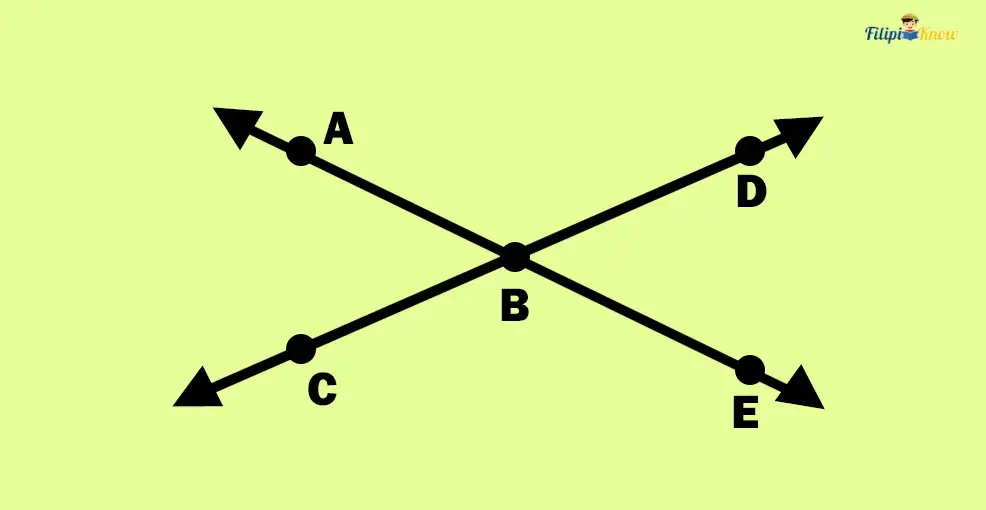
∠ABC and  ∠DBE are vertical angles. As per the vertical angle theorem, we can conclude that they are congruent. For instance, if the measure of ∠ABC is 45 degrees, m∠DBE is also 45 degrees.

Sample Problem: Using the same figure above, if ∠CBE = 2x + 20 and ∠ABD = 120°. What is the value of x?

Solution: We know that angles ∠ABD and ∠CBE are vertical angles. Thus, they are congruent or have equal measures:

m∠ABD = m∠CBE

120 = 2x + 20

2x + 20 = 120 Symmetric property

2x = -20 + 120                      Transposition method

2x = 100

2x/2 = 100/2 

x = 50

Thus, the value of x is 50.

2. Complementary Angles

If the measurements of two angles have a sum of 90 degrees, the angles are complementary.

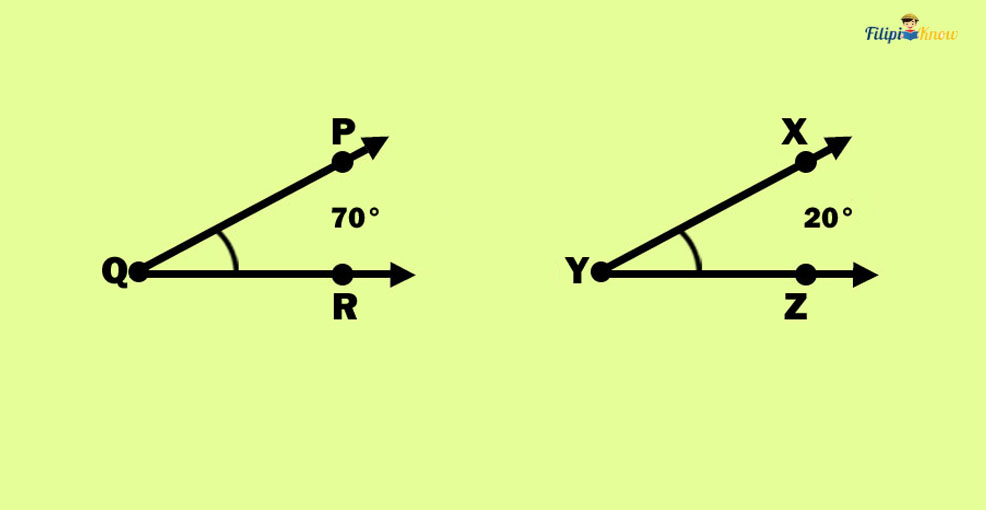
∠PQR and ∠XYZ are complementary angles since the sum of their measurements is 90 degrees.

3. Supplementary Angles

Supplementary angles are almost similar to complementary angles, except that the sum of their measures must equal 180 degrees. Thus, we can define supplementary angles as a pair of angles whose sum of measurements is 180 degrees. 

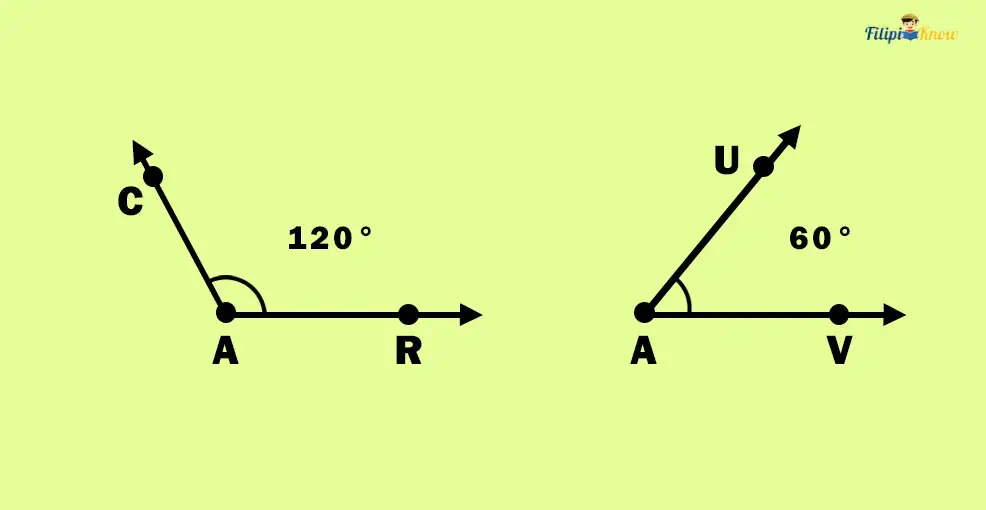
In the image above, angles ∠CAR and ∠UAV are supplementary angles since the sum of their measurements is 180 degrees. 

Let us solve some problems involving complementary and supplementary angles.

Sample Problem 1: An angle is a complement of another angle. If the measure of one of these angles is twice the measure of the other angle, what is the measure of the shorter angle?

Solution: 

The problem does not provide us with any measurement of the angles. The only thing that we know is that they complement each other. Thus, we can state that the sum of these two angles is 90°.

First angle + Second angle = 90°.

The problem stated that the measure of one angle is twice the other, meaning that one angle is larger in measure than the other. To make our equation above more detailed:

Smaller angle + Larger angle = 90°.

Let x be the measure of the smaller angle. The measure of the larger angle is twice, or two times, the smaller, so we let 2x be the measure of the larger angle:

x + 2x = 90

We can now solve the value of x above:

x + 2x = 90 

3x = 90 Combining like terms

3x∕3 = 90∕3 Dividing both sides of the equation by 3

x = 30

Since x represents the measure of the smaller angle, the smaller angle has a degree measure of 30 degrees. 

Sample Problem 2: Angles 1 and 2 are supplementary. Angle 1 measures 60 degrees larger than twice the measure of angle 2. What is the measure of an angle that is complementary to angle 2?

Solution: 

The first thing we have to do is determine the measurements of angles 1 and 2.

It states that angles 1 and 2 are supplementary. Hence, the sum of their measurements must be 180:

Angle 1 + Angle 2 = 180 

The measurement of angle 1 is 60 degrees larger than twice the measurement of angle 2. Thus, angle 1 is larger than angle 2 (keep this in mind!)

Let x be the measure of angle 2.

Again, the measurement of angle 1 is 60 degrees larger than twice the measurement of angle 2. We can express the measurement of the angle as 2x + 60 (2x is twice the measure of the other angle while the “plus 60 degrees” is for the “60 degrees larger” part of angle 1’s description).

Again, x is the measurement of angle 2. 2x + 60 is the measurement of angle 1:

Going back to the earlier equation we established:

angle 1 + angle 2 = 180 

(2x + 60) + x = 180

Let’s solve for x in the equation we formed above:

(2x + 60) + x = 180

3x + 60 = 180 Combining like terms

3x = -60 + 180           Transposition method

3x = 120

3x∕3 = 120∕3 Dividing both sides by 3

x = 40

Therefore, angle 2 measures 40°.

However, we are not done yet. The problem is not asking us to find the measurement of angle 2; instead, it’s asking us to find the measurement of its complement. The complement of angle 2 is just the angle such that when it is added to the measure of angle 2, the result will be 90°.

So, to find the measurement of the complement of angle 2, we subtract 40° from 90°:

90° – 40° = 50°

So, the final answer for this problem is 50°.

4. Adjacent Angles and Linear Pairs

The angles are adjacent if two angles have a common vertex and a common side (or ray).

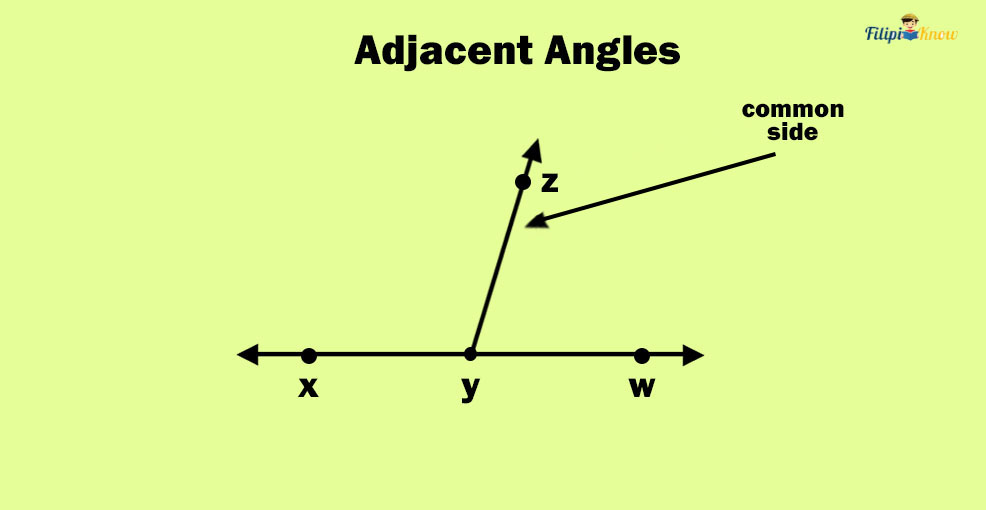
In the figure above, ∠XYZ and ∠WYZ share a common vertex, point Y, and a side, ray YZ. Thus, ∠XYZ and ∠WYZ are adjacent angles.

Now, if two adjacent angles are supplementary, then these angles are called linear pairs. Linear pairs will form a side which is a straight line. 

In the previous figure, ∠XYZ and ∠WYZ form a side that is a straight line (line XW). Thus, ∠XYZ and ∠WYZ are linear pairs, and they are supplementary. 

Sample Problem: ∠ABC and ∠CBE are linear pairs. Determine the measure of ∠ABC if m∠CBE = 70 degrees. 

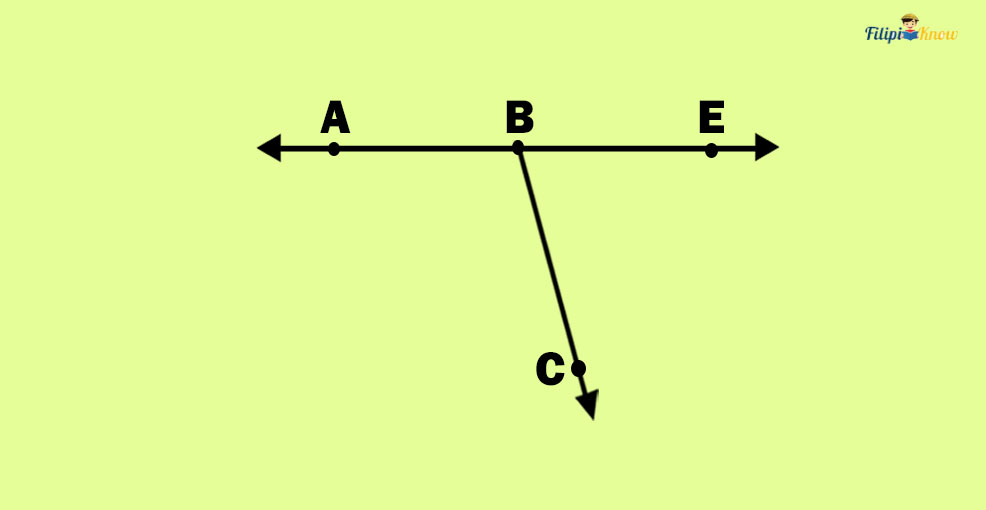
Since ∠ABC and ∠CBE are linear pairs, then they are supplementary. We know that the measurements of supplementary angles have a sum of 180 degrees.

To find the measure of ∠CBE:

m∠ABC = 180 – 70 = 110

Thus, the answer is 110 degrees.

Angles Formed by Transversal Intersecting Parallel Lines

As a review, parallel lines do not meet or intersect.

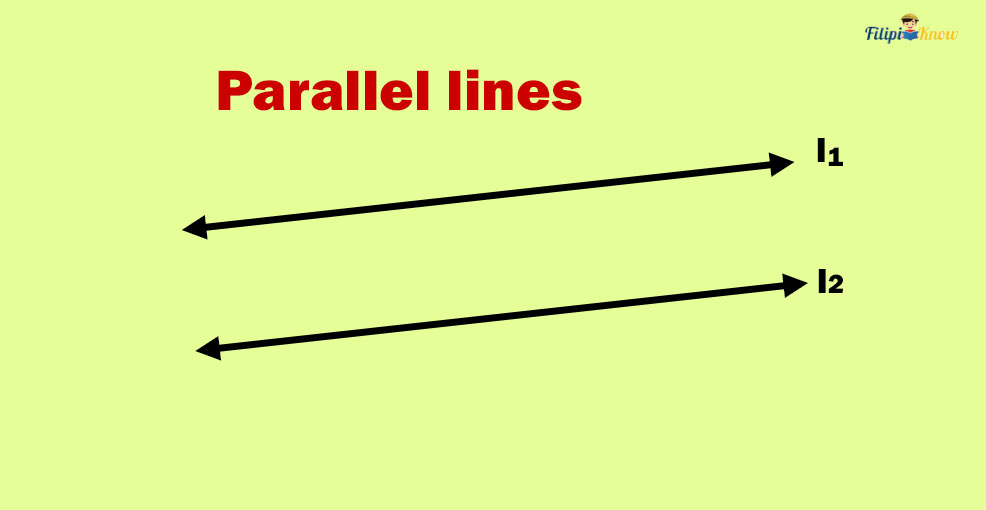
As you can see, lines l₁ and l₂ are parallel since they do not meet. Even if we extend the length of lines infinitely, certainly, they will never intersect.

We use the symbol || to indicate that two lines are parallel. Hence, we can state “line l₁ and l₂ are parallel” in symbols as l₁ || l₂

Now, if a line intersects two parallel lines (refer to the figure below), that line is called a transversal line.

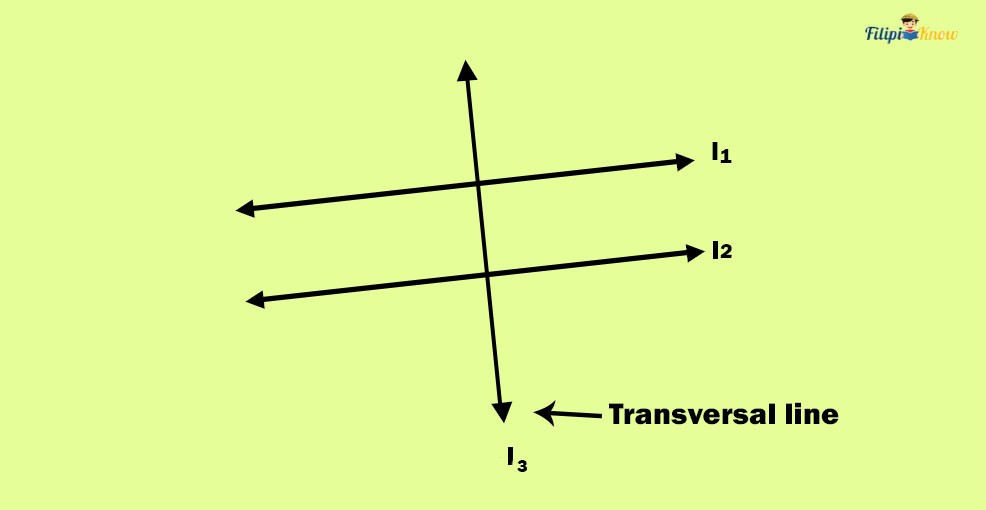
In the figure above, l₃ is a transversal line since it intersects two parallel lines, l₁ and l₂.

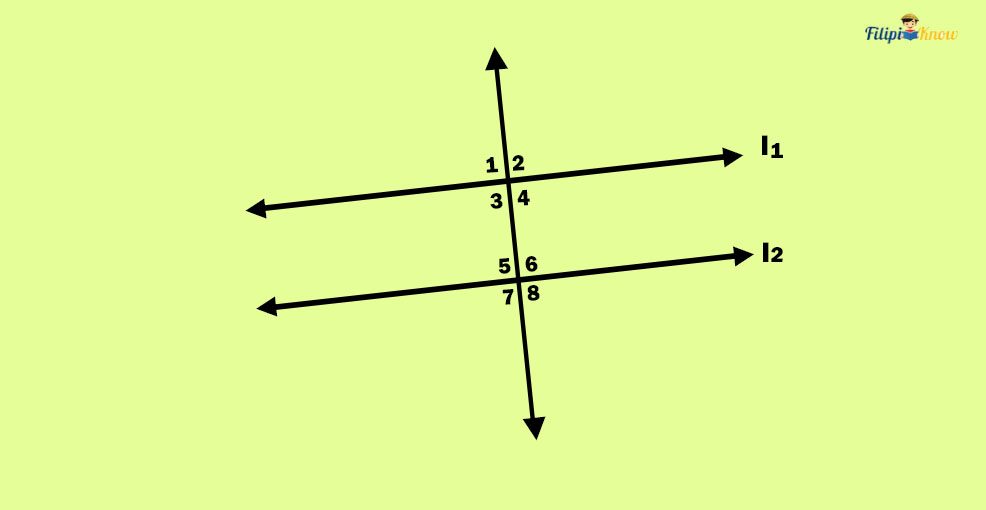
When a transversal line intersects parallel lines, it is noticeable that various angles are formed. Throughout this review, we will use numbers to identify the angles formed by transversal intersecting parallel lines. As you can see, eight angles were created, called transversal angles. The following section will discuss how these transversal angles are related.

1. Corresponding Angles

Corresponding angles are transversal angles on the same side of the transversal and have sides on the transversal going in the same direction. Their other sides go in parallel directions.

 

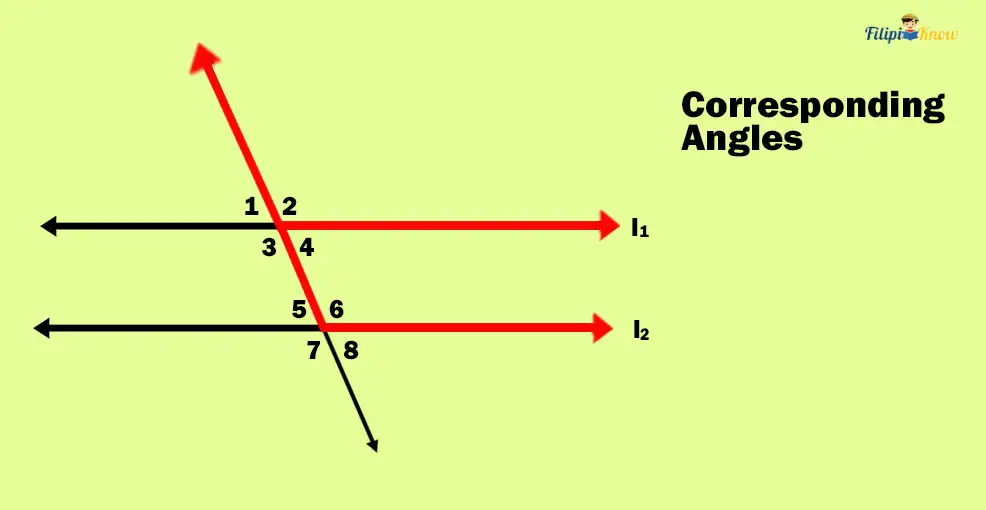
In the figure above, angles ∠2 and ∠6 are on the same side of the transversal, with sides on the transversal going in the same direction and their other sides in parallel directions. Likewise, ∠3 and ∠7 are corresponding angles because they exhibit the same properties.

On the other hand, ∠2 and ∠8 are not corresponding angles because although they are on the same side, their figures are not matching.

Here’s an important theorem about corresponding angles.

Corresponding Angle Theorem

“If two parallel lines are cut by a transversal, then the pairs of corresponding angles are congruent.”

So, in the figure above, corresponding angles ∠2 and ∠6 have the exact measurement. So, if m∠2 = 30°, m∠6 should be 30° also. 

Sample Problem 1: In the figure below l₁ || l₂, if m∠6 = 70°, determine m∠8.

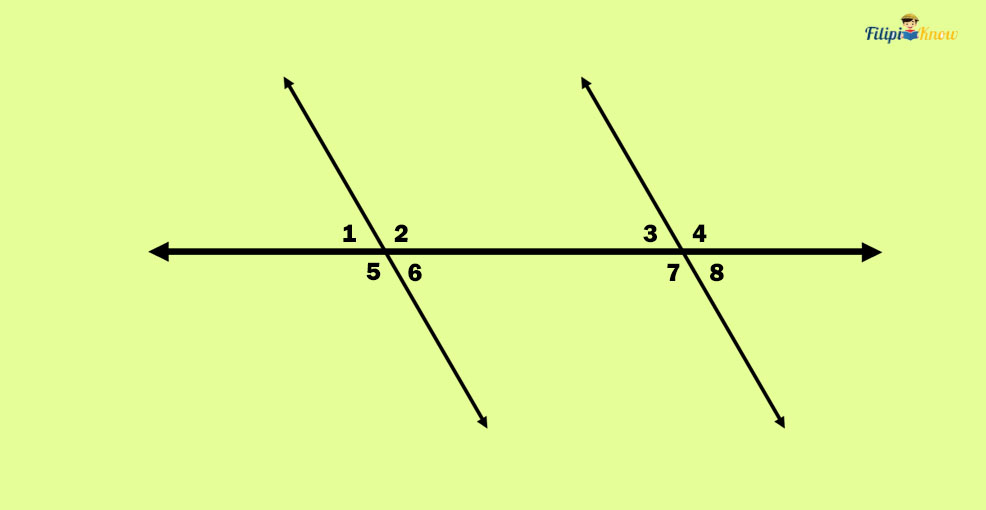
Solution: In the figure above, angles 6 and 8 are corresponding angles since they are on the same “side” (below the transversal) and have matching figures. Therefore, we can state that angles 6 and 8 are congruent. If m∠6 = 70°, then m∠8 = 70°.

Sample Problem 2: Using the exact figure in the previous example, if m∠8 = 70°, determine m∠3.

Solution: If you retake a look at the figure, you will notice that angles ∠3 and ∠8 are vertical since they create two pairs of opposite rays. We know that vertical angles are congruent, so if m∠8 = 70°, then m∠3 = 70°

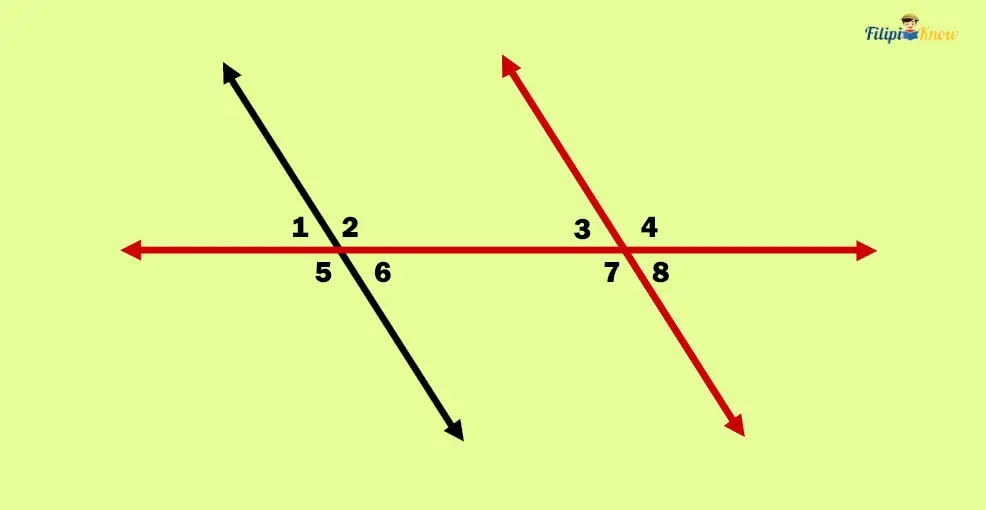
Sample Problem 3: Using the exact figure in the previous example, if m∠8 = 70°, determine m∠7.

Solution: Notice that angles 7 and 8 are linear pairs since they share a common side, and their sides form a straight line. From our previous discussion about linear pairs, we have learned that linear pairs are supplementary. So, angles 8 and 7 are supplementary angles:

Supplementary angles have a sum of measures of 180 degrees:

 m∠7 +  m∠8 = 180

We know that m∠8 is 70 degrees:

 m∠7 +  70 = 180

Solving for m m∠7:

m∠7 = 180 – 70 = 110°

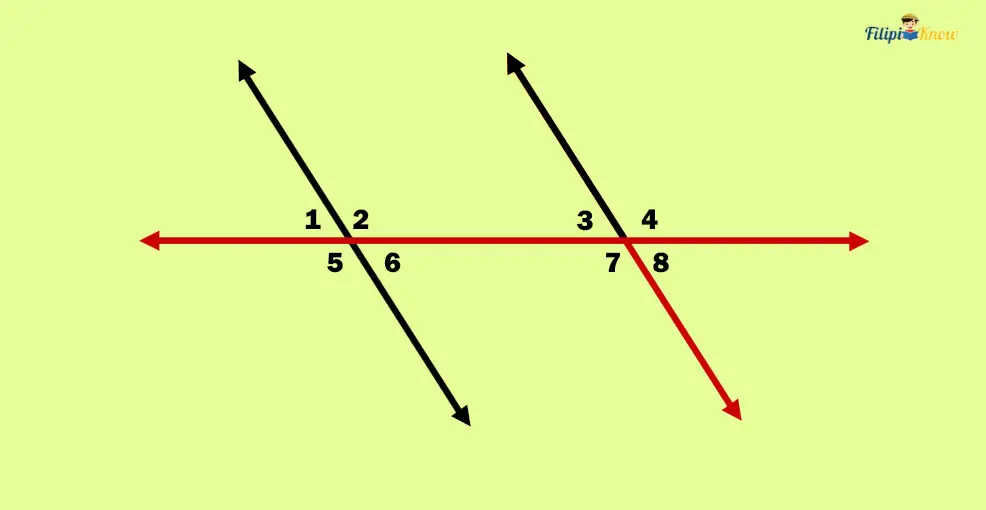
2. Alternate Interior Angles

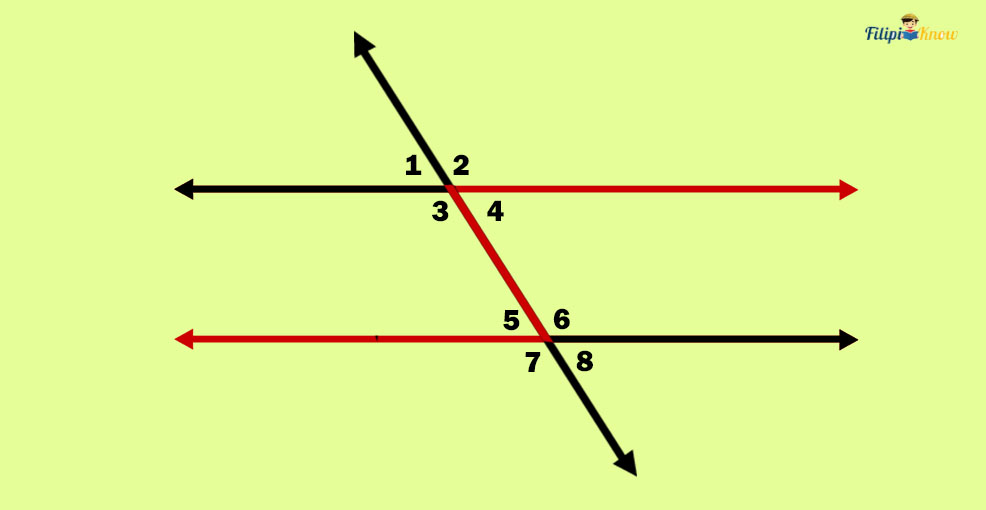
Alternate interior angles are transversal angles in the inner portion of the parallel lines but on the opposite side of the transversal.

In the figure above, angles 4 and 5 are alternate interior angles since they are in the interior portion of the parallel lines and on the opposite sides of the transversal (angle 4 is on the right side, angle 5 is on the left side). 

Angles 3 and 6 are also alternate interior angles.

If you have noticed, alternate interior angles form this weird letter “S” shape. If you look again at angles 4 and 5, they form a letter “S”-like figure. Angles 3 and 6 also form the inverse of this letter “S”-like figure. Look at the figure below to better visualize alternate interior angles. 

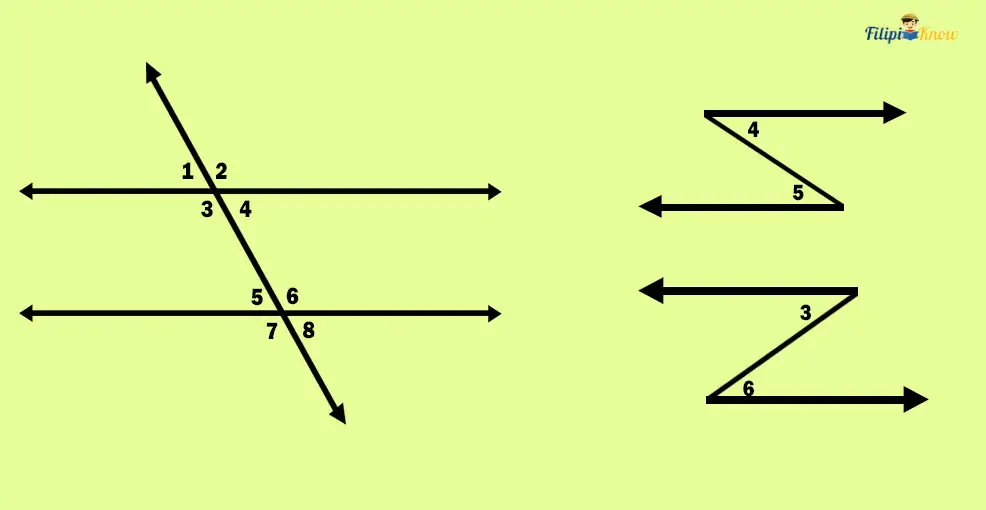
Here’s an essential theorem about alternate interior angles:

Alternate Interior Angle Theorem

“If two parallel lines are cut by a transversal, the alternate interior angles formed are congruent.”

The theorem above tells us that alternate interior angles have the exact measurement.

Looking at the figure above, we can state that angles 4 and 5 are congruent since they are alternate interior angles. Moreover, we can also say that angles 3 and 6 are congruent since they are alternate interior angles.

3. Alternate Exterior Angles

Alternate exterior angles are the opposite of the alternate interior angles. Alternate exterior angles are a pair of angles in the outer portion of the parallel lines and on the opposite sides of the transversal line.

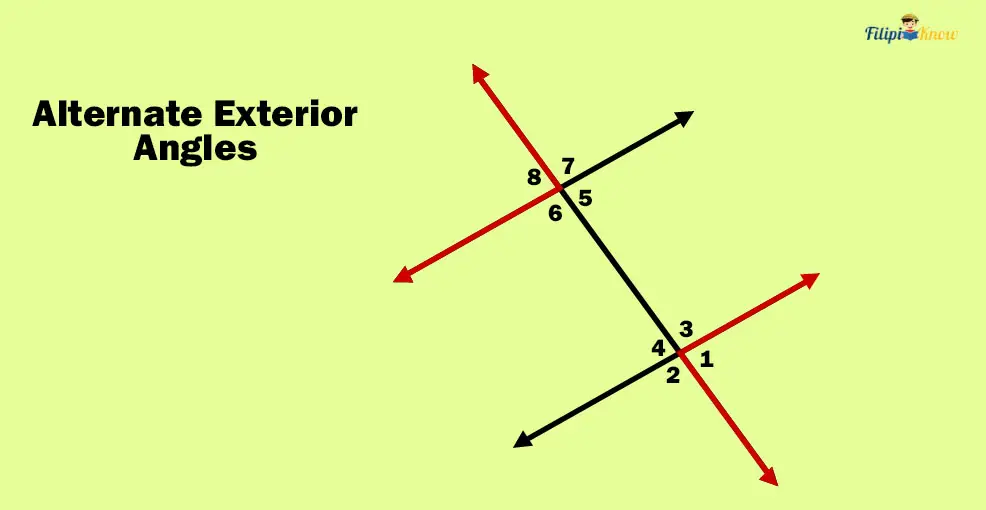
In the figure above, ∠1 and ∠8 are alternate exterior angles since they are both on the exterior of the parallel lines and the opposite sides of the transversal (∠1 is on the right side of the transversal, and ∠8 is on the left side). 

There’s an important theorem regarding alternate exterior angles. It is stated below.

Alternate Exterior Angle Theorem

“If two parallel lines are cut by a transversal, the alternate exterior angles formed are congruent.”

The theorem above tells us that if two angles are alternate exterior angles, then these angles have an equal measurement or are congruent.

Hence, in the figure above, we can conclude using the theorem that angles 1 and 8 are congruent or have the exact measurement since they are alternate exterior angles.

Sample Problem: Using the given figure below, determine the measurements of angles ∠2, ∠3, ∠6, and ∠8 if m∠1 = 80°

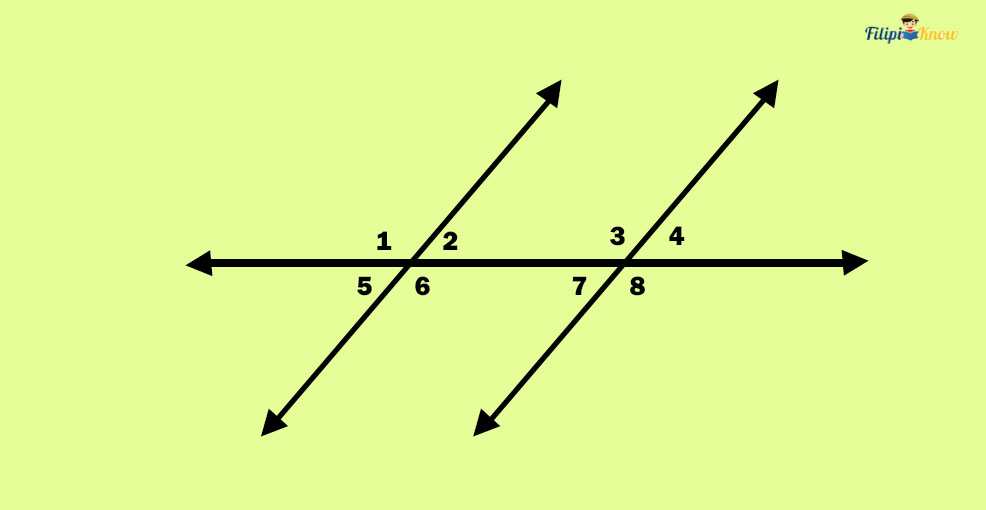
Solution:

Let us start determining the degree measure of ∠2. Looking at the figure above, you will notice that angles ∠1 and ∠2 are linear pairs since they share a common side, and their remaining sides form a straight line. We know that linear pairs are supplements of each other, so the sum of measures of ∠1 and ∠2 should be 180°:

m∠1 + m∠2 = 180°

It is given that m∠1 = 80°, so let’s plug it into the equation above:

80 + m∠2 = 180° 

m∠2 = 180 – 80 

m∠2 = 100° 

As we can see, the computed measure of ∠2 is 100° or m∠2 = 100°.  

Now, let us determine the measure of ∠3. Retake a look at the given figure. What can you say about ∠1 and ∠3? Yes, they are corresponding angles.

As per the previous theorem we have discussed, corresponding angles are congruent. Since ∠1 and ∠3 are congruent, these angles have the exact measurement. So, if m∠1 = 80°, m∠3 should also equal 80°. Thus, m∠3 = 80°.

This time, let us determine the measure of ∠6. Which angle do you think we can use to determine the measurement of ∠6?? Well, you can use either angle 1 or angle 2.

If you use ∠1, then ∠1 and ∠6 are vertical angles. Since vertical angles are congruent (per the vertical angle theorem), if m∠1 = 80°, then m∠6 = 80°.

On the other hand, if you use ∠2 instead, ∠2 and ∠6 are linear pairs. Since linear pairs are supplements of each other, then the sum of their measurement is 180°. We have computed earlier that m∠2 = 100°, so to find the measure of ∠6:

m∠6 = 180 –  m∠2 

m∠6 = 180 – 100

m∠6 = 80° 

Hence, m∠6 = 80° 

Note that whether you use angle 1 or 2, you can still derive the exact measurement for angle 6. 

Lastly, to find the measurement of ∠8, we can use the measurement of ∠1. ∠1 and ∠8 are alternate exterior angles since they are both located in the exterior portion of the parallel lines and are on the opposite sides of the transversal line (look at the given figure above). We know that alternate exterior angles are congruent based on a previous theorem. Hence, if m∠1 = 80°, then m∠8 = 80°.

Interior Angles of a Polygon

Angles that are located inside a polygon are called interior angles. As you may recall, a polygon is a plane figure composed of sides and vertices where these sides meet. Take a look at the triangle ABC (or △ABC) below: 

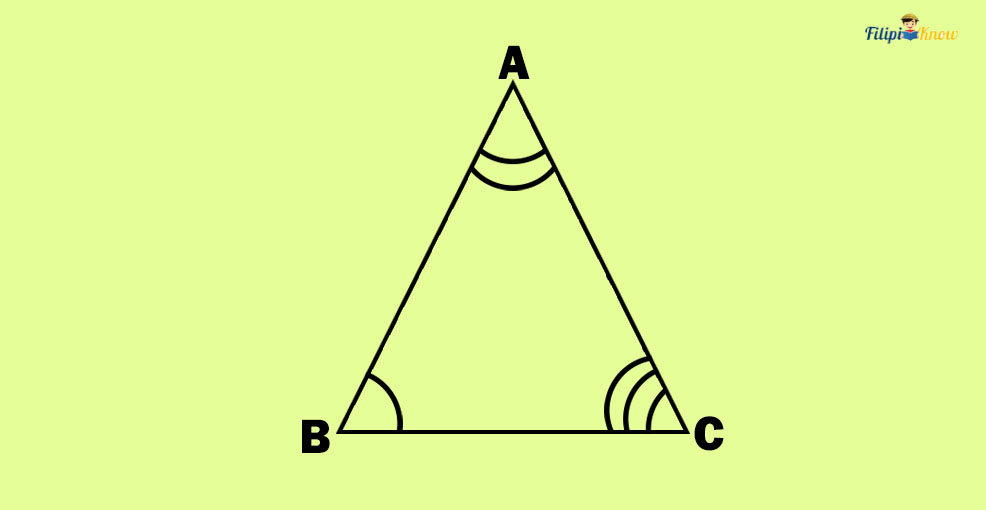
The triangle above has three interior angles: ∠ABC, ∠ACB, and ∠BAC. We put arcs in the triangle to indicate these interior angles. 

Did you know that if you draw any triangle, the total measurement of its interior angles will always be 180°?

Yes, the sum of the interior angles of any triangle indeed is 180°. We state this concept formally in the theorem below:

Triangle Sum Theorem

“The sum of the measurements of all the interior angles of any triangle is 180°.”

So, whether you, your friend, or a stranger draws a triangle, the sum of the interior angles of that triangle will always be precisely 180°. 

Sample Problem: If m∠ABC = 3x + 15, m∠ACB = x + 20, and m∠BAC = x, determine the value of x (refer to the figure below).

Solution: 

Since the given angles are interior angles of the triangle above, we are sure that the sum of the measurements of these angles is 180° because of the triangle sum theorem.

m∠ABC + m∠ACB + m∠BAC = 180°

(3x + 15) + (x + 20) + x = 180° Input the given values in the problem

5x + 35 = 180° Combining like terms

5x = -35 + 180 Transposition method

5x = 145

5x∕5 = 145∕5 Dividing both sides of the equation by 5

x = 29

Thus, the value of x is 29.

General Formula for the Sum of Interior Angles of a Polygon

A polygon with n sides has n interior angles. So, if a triangle has three sides, then it has three interior angles also. Meanwhile, a square has four sides, so it has four interior angles as well. A pentagon has five sides, so it has five interior angles also.

We have learned in the previous section that the sum of the interior angles of a triangle is always 180°. How about quadrilaterals, pentagons, hexagons, or decagons? How do we find the sum of their interior angles?

We can use a general formula to determine the sum of the interior angles of a polygon with n sides. This formula is presented below:

The formula gives the sum of the interior angles of a polygon with n sides:

Sum of interior angles = 180(n – 2)

So, a quadrilateral that has n = 4 sides has a sum of interior angles:

Sum of interior angles = 180(4 – 2) = 180(2) = 360°

Any quadrilateral (four-sided polygon) such as square, rectangle, parallelogram, trapezoid, etc., will always have a sum of measurements of interior angles equal to 360°

Sample Problem: A polygon has 12 sides (i.e., dodecagon). What is the sum of its interior angles?

Solution: 

Using our formula and n = 12:

Sum of interior angles = 180(n – 2)

Sum of interior angles = 180(12 – 2) 

Sum of interior angles = 180(10) = 1800°

Hence, the sum of the measurements of the interior angles of a dodecagon is 1800°.

Measure of an Interior Angle of a Regular Polygon

As a consequence of the formula above, if a polygon is a regular polygon (which means that all of its sides and angles are congruent), then the measurement of an interior angle of a regular polygon with n sides can be computed as:

Suppose an equilateral and equiangular triangle where all of its sides and angles are congruent. Now, the measure of one of its angles can be calculated using the formula above. 

Using n = 3:

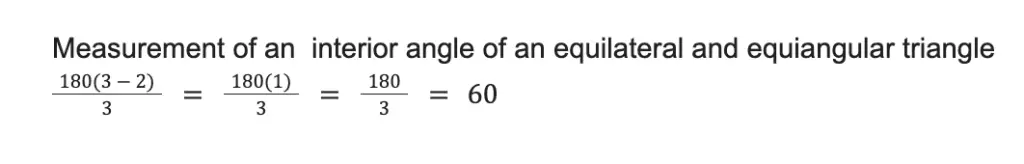
Thus, the measure of an interior angle of an equilateral and equiangular triangle is 60°.

Sample Problem: A regular polygon has n = 10 sides (decagon). Determine the measurement of one of its interior angles.

Solution: 

Using the formula for the measurement of an interior angle of a regular polygon:

Using n = 10:

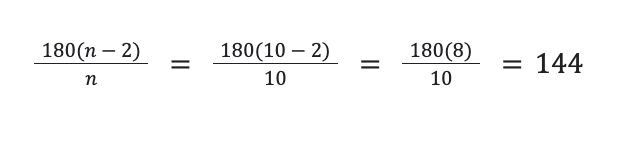
Thus, the measure of an interior angle of a regular polygon with ten sides (decagon) is 144°.

Perpendicularity

If two lines intersect and form right angles, these lines are perpendicular. In other words, perpendicular lines form right angles.

An informal way to detect perpendicular lines is by looking at the “T shape” formed by these lines. Notice that perpendicular lines form a letter “T” or an inverted letter “T.”

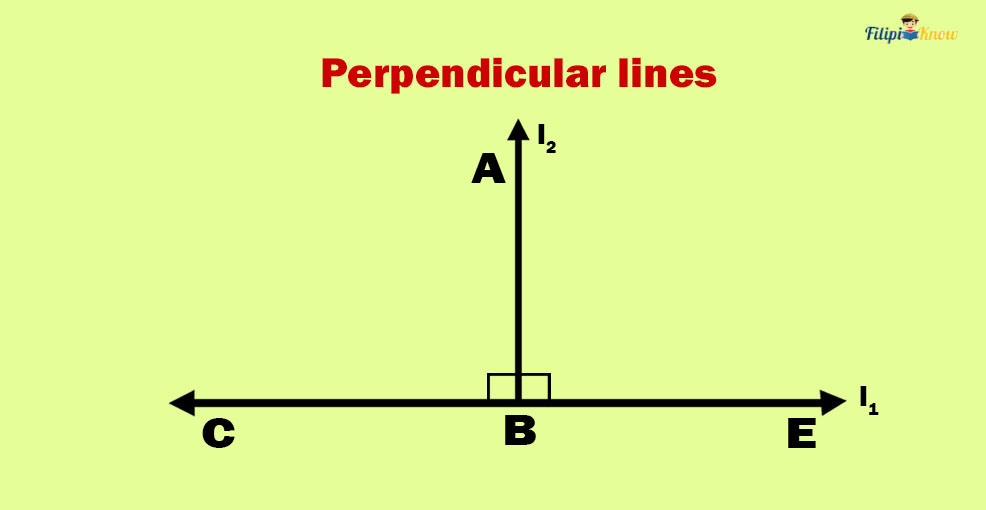
In the figure above, lines l₁ and l₂ are perpendicular. We use the symbol ⊥ to indicate that two lines are perpendicular. Hence, l₁ ⊥ l₂. Since these lines are perpendicular, ∠ABC and ∠ABE are right angles with m∠ABC and m∠ABE equal 90 degrees.

In addition to this, as you can see above, the angles formed by perpendicular lines are also linear pairs since they share a common side (in the figure above, ray AB) and their remaining sides form a straight line, 

Sample Problem: Lines l₁ and l₂ are perpendicular. If angle 1 measures x degrees and angle 2 measures x + 40 degrees, what is the value of x?

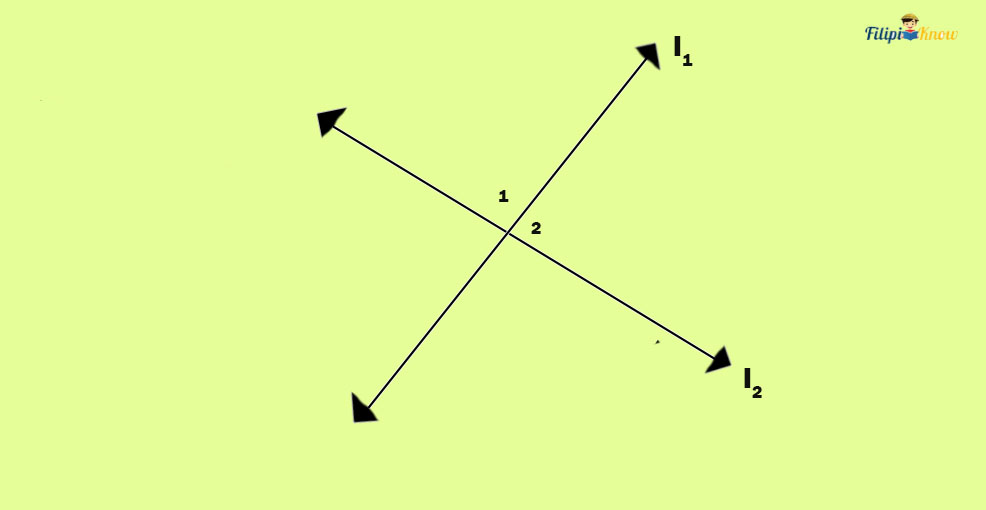
Solution: Since l₁ and l₂ are perpendicular lines, angles 1 and 2 are linear pairs. If two angles are linear pairs, they are supplementary, or the sum of their degree measurements equals 180°.

Thus, we have:

Measurement of angle 1 + Measurement of angle 2 = 180°

(x) + (x + 40) = 180°

Combining like terms:

2x + 40 = 180

By transposition:

2x = -40 + 180

2x = 140

Dividing both sides of the equation by 2:

2x/2 = 140/2

x = 70

Thus, the value of x is 70. 

Next topic: Triangles

Previous topic: Introduction to Geometry: Undefined Terms, Definition, Postulates, and Theorems

Return to the main article: The Ultimate Basic Math Reviewer

Download Printable Summary/Review Notes

Download Printable Flashcards

Test Yourself!

1. Practice Questions [Free PDF Download]

2. Answer Key [Free PDF Download]

3. Math Mock Exam + Answer Key