To determine a person’s location, we usually refer to that person’s address. We use a mathematical coordinate system to locate a specific point through numerical coordinates.

In this review, we’ll study the Cartesian coordinate system used to solve geometric problems algebraically, which has paved the way for creating different modern technologies such as GPS navigation. In particular, we will learn how to plot a point in the coordinate system; graph a line based on a given equation and compute its slope; analyze parallel and perpendicular lines in the coordinate plane, and graph some common mathematical functions. 

Click below to go to the main reviewer:

Ultimate UPCAT Reviewer

Ultimate PMA Entrance Exam Reviewer

Ultimate LET Reviewer

Introduction to the Cartesian Coordinate System

French mathematician and philosopher Rene Descartes developed the Cartesian coordinate system. One day, while watching a fly on the ceiling from his bed, Descartes tried to describe the insect’s location mathematically. And this is how the coordinate system was supposedly born.

The coordinate system that Descartes developed eventually bridged the gap between algebra and geometry. We can provide visual representations of different mathematical expressions or functions through the coordinate system. Furthermore, using the coordinate system, we can describe geometric figures and prove some of their properties through algebraic expressions.

For instance, when you graph a linear equation in the coordinate system, you will have a straight line formed using two points. On the other hand, if you plot a quadratic equation in the coordinate system, you will derive a curve known as a parabola. Meanwhile, plotting x² + y² = c where c is some real number will obtain a circle.

 

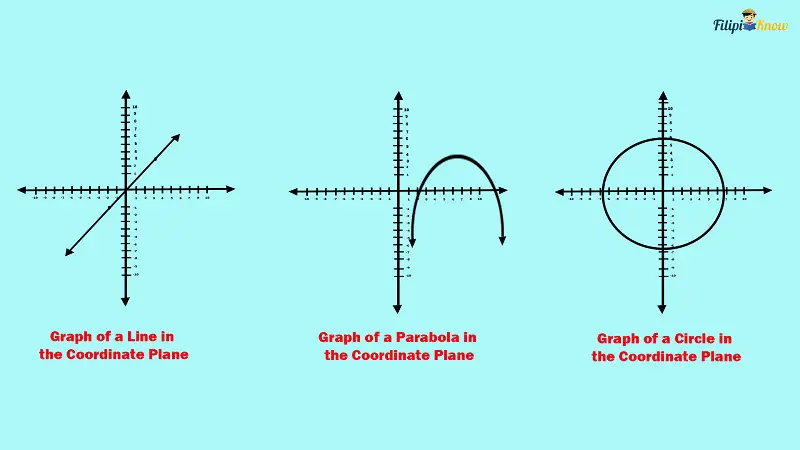
The Cartesian Coordinate System

The Cartesian coordinate system comprises two axes intersecting and perpendicular to each other. Note that when we say “perpendicular,” the lines form right or  L-shaped angles. The horizontal axis (i.e., the horizontal line) that you see is called the X-axis. On the other hand, the vertical axis (i.e., the vertical line) is called the Y-axis.

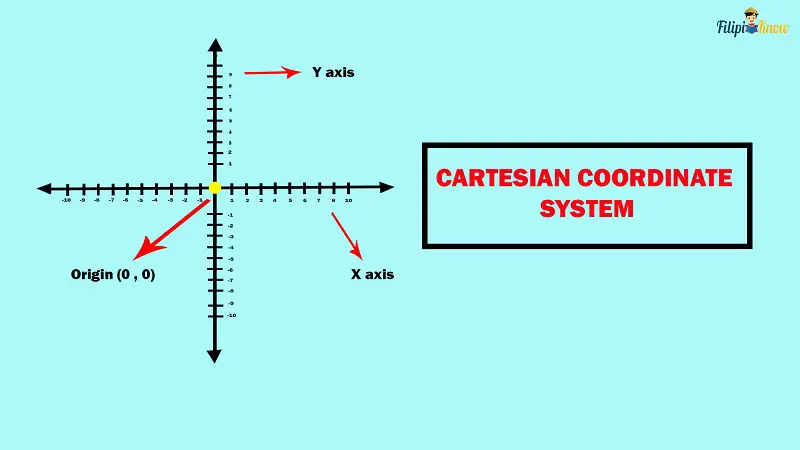
As you can see above, both the X-axis and the Y-axis are number lines. The X-axis has positive numbers on the right and negative numbers on the left. On the other hand, the Y-axis has positive numbers in the upper portion while it has negative numbers in the lower portion.

The X-axis and Y-axis intersect at the point (0, 0). This point is known as the origin.

There are different ways to call the Cartesian coordinate system. Sometimes it is referred to as the rectangular coordinate system, coordinate system, or simply the coordinate plane.

Plotting a Point in the Coordinate Plane

When we say “plot a point” in the coordinate plane, we mean to mark a point in the coordinate plane using the numbers on the X-axis and Y-axis as references. 

Let’s say we want to plot the point (5, 7) in the coordinate plane. To plot this point, you need to count five units on the right of the origin and then seven units upward.

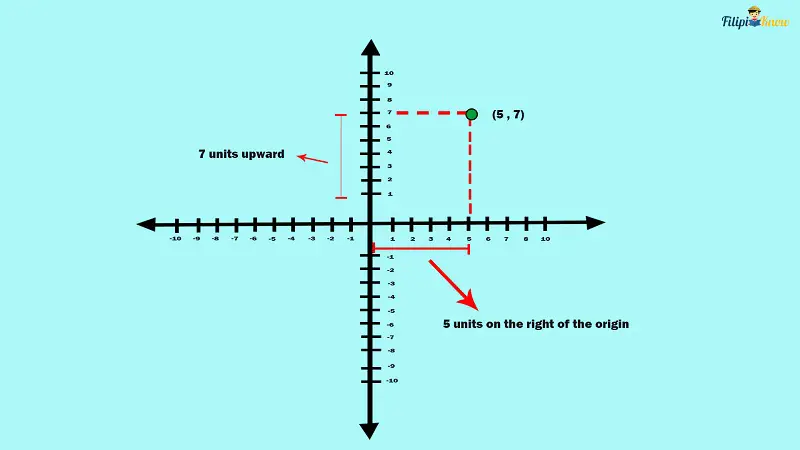
There you go! You have plotted the point (5, 7) in the coordinate plane.

A point in the coordinate plane is also called a coordinate or an ordered pair.  As you have seen, a coordinate is composed of two numbers or components. For instance, the coordinate we have plotted above, which is (5, 7), consists of two numbers, 5 and 7. The first number, 5, is called the x-coordinate or the abscissa. On the other hand, the second number, which is 7, is called the y-coordinate or the ordinate.

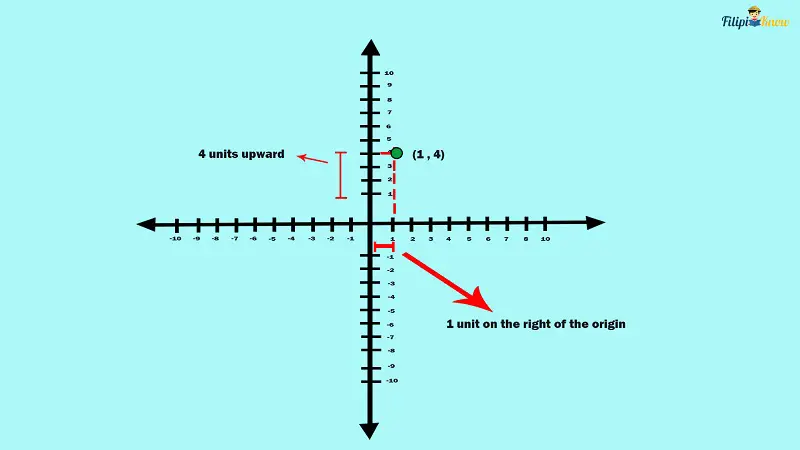
Example 1: Determine the abscissa and ordinate of (1, 4). Afterward, plot the point in the coordinate plane.

Solution: The abscissa is the x-coordinate of (1, 4) which is 1. On the other hand, the ordinate is the y-coordinate of (1, 4) which is 4. To plot (1, 4) in the coordinate plane, we count 1 unit to the right of the origin and move 4 units upward.

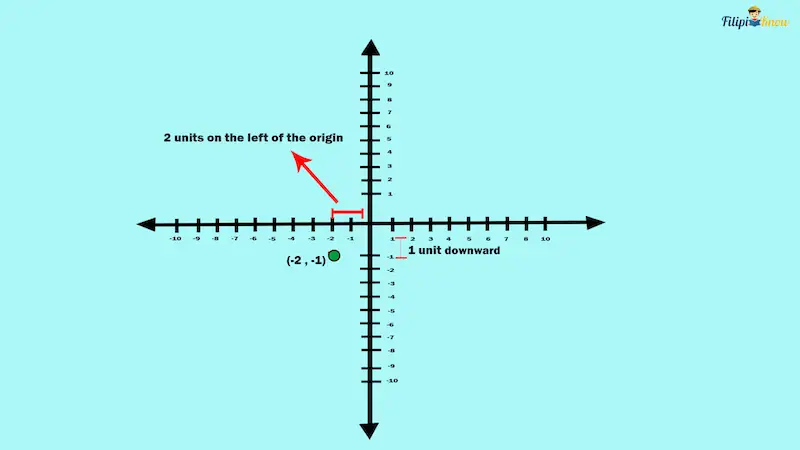
Example 2: Plot (-2, -1) in the coordinate plane.

Solution: To plot (-2, -1) in the coordinate plane, we count two units on the left of the origin and move one unit downward.

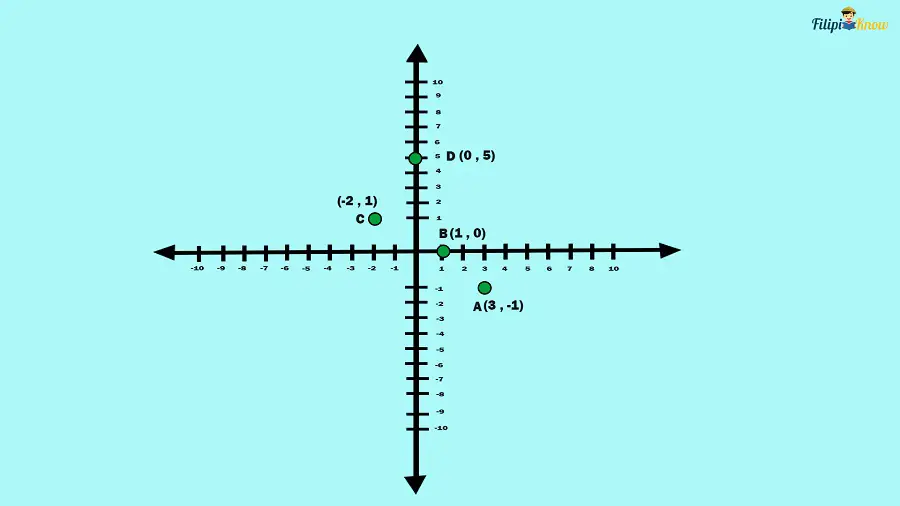
Example 3: Try to plot the following points by yourself:

A. (3, -1)

B. (1, 0)

C. (-2, 1)

D. (0, 5)

Solution:

Here are the answers:

The Four Quadrants of the Cartesian Coordinate System

Looking closely at the coordinate plane, you will notice that the entire rectangular plane is divided into four sections. These sections are called the quadrants of the coordinate plane.

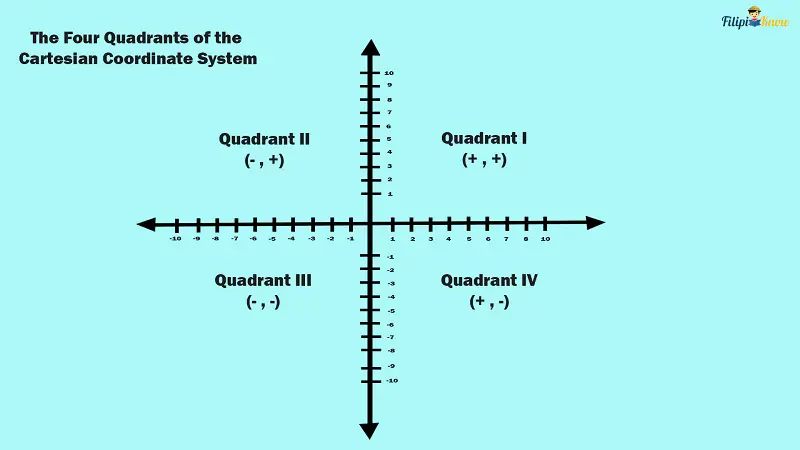
The quadrants of the coordinate plane are arranged in a counter-clockwise manner. The first quadrant is the quadrant where the positive portions of the X-axis and Y-axis are located. The following list provides an overview of all four quadrants:

• All coordinates with positive first and second components are in the first quadrant.
• All coordinates with a negative first component and a positive second component are in the second quadrant.
• All coordinates with negative first and second components are in the third quadrant.
• All coordinates with a positive first component and a negative second component are in the fourth quadrant.

Example: In which quadrant can you locate (-2, 1)?

Solution: (-2, 1) has a negative first component and a positive second component. Therefore, we can locate (-2, 1) in the second quadrant of the coordinate plane.

 

Straight Lines in the Coordinate Plane

According to Euclidean geometry, two points determine a straight line. Hence, you can connect two points to form a straight line in a coordinate plane.

Example: Form a straight line using the points (2, 3) and (5, 1).

Solution: We start by plotting the points in the coordinate plane.

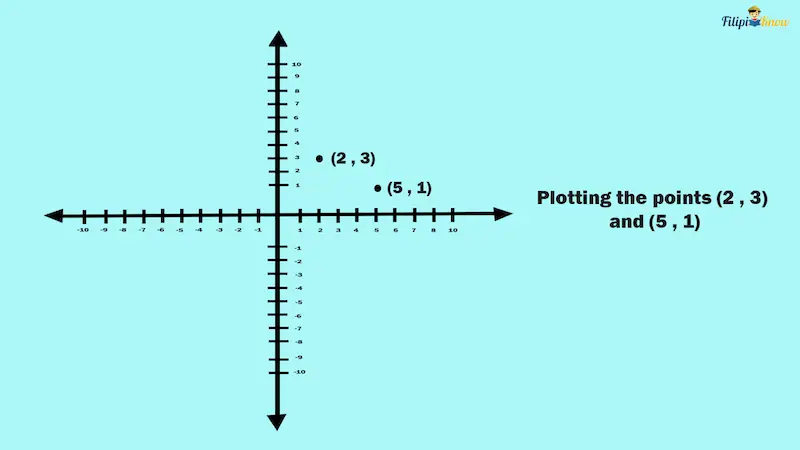
Afterward, we connect the points to form a straight line.

There you go! We have just graphed a line that passes through the points (2, 3) and (5, 1).

 

Linear Equations in the Coordinate Plane

In the previous section, I showed you how to graph a straight line in the coordinate plane using two given points. But what if the given problem is a linear equation?

We will graph the type of linear equation in the ax + by = c form. In other words, linear equations in two variables, x, and y.

Let’s use the linear equation x + y = 10 as an example. If you graph it in the coordinate plane, it will look like this:

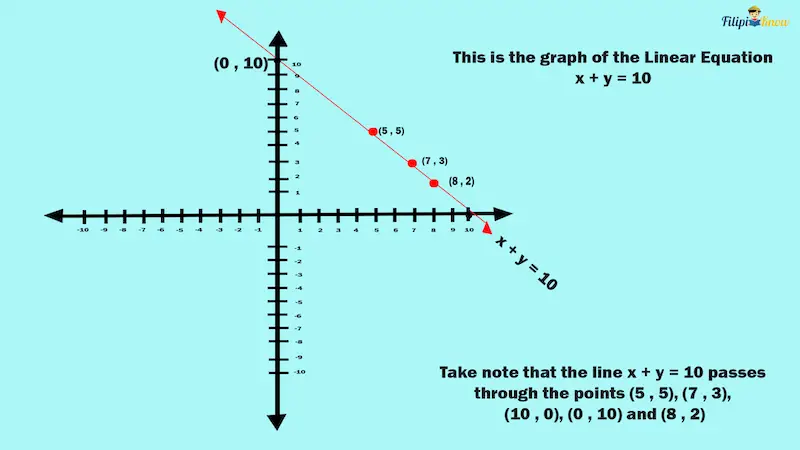
The red line above is the graph of x + y = 10. All points within the red line will provide the values of x and y that will satisfy the linear equation x + y = 10.

For instance, (8, 2) is a point within the red line. This means that x = 8 and y = 2 will satisfy the x + y = 10 equation. 

x + y = 10

(8) + (2) = 10 at (8, 2) or x = 8 and y = 2

10 = 10

Notice also that the points (7, 3), (5, 5), and (10, 0) are within the line. If you try to verify these points individually, you will see that they all satisfy the equation. 

On the other hand, (1, 6) is not in the line; this point doesn’t satisfy the linear equation x + y = 10.

Therefore, the points on the graph of a linear equation are the set of points or values of x and y that satisfy the linear equation.

Intercepts of a Linear Equation

The intercepts of a linear equation are the part of the line that touches the X-axis and Y-axis. For instance, look at the graph of x + y = 10 again:

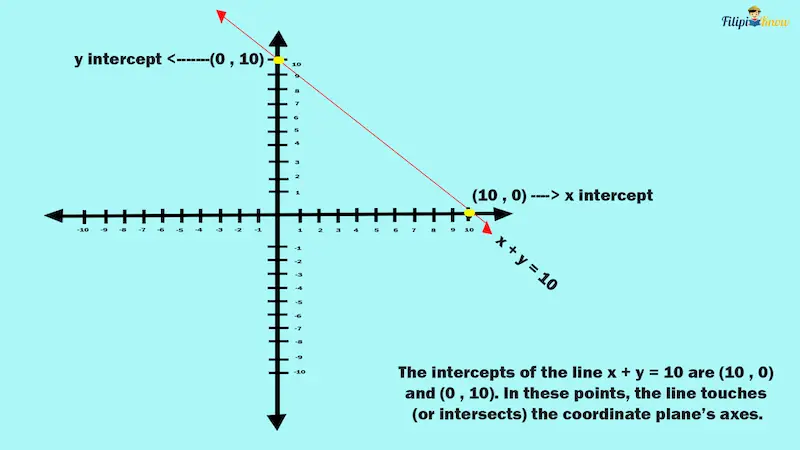
Notice that the line touches the X-axis at the point (10, 0). Hence, the point (10, 0) is called the x-intercept of the line. On the other hand, at the point (0, 10), the line touches the Y-axis. Hence, the point (0, 10) is called the y-intercept of the line.

Therefore, the x-intercept of the line is where the line touches the x-axis, while the y-intercept is where the line touches the y-axis.

How to Determine the Intercepts of a Linear Equation.

The x-intercept can be calculated by setting the value of the y variable of the linear equation to zero. Afterward, solve for the value of x. 

On the other hand, the y-intercept can be calculated by setting the value of the x variable of the linear equation to zero. Afterward, solve for the value of y.

Example: Solve for the intercepts of the line x + 2y = 8.

Solution: To solve for the x-intercept of the line, set y = 0

x + 2y = 8

x + 2(0) = 8 Set y = 0

x = 8

Hence, the x-intercept is (8, 0).

On the other hand, to find the y-intercept, we let x = 0

x + 2y = 12

(0) + 2y = 8 Set x = 0

2y = 8

2y⁄2 = 8⁄2 Divide both sides by 2

y = 4

Hence, the y-intercept is (0, 4).

Graphing a Linear Equation Using Its Intercepts

You can graph a linear equation once you have identified its x and y intercepts.

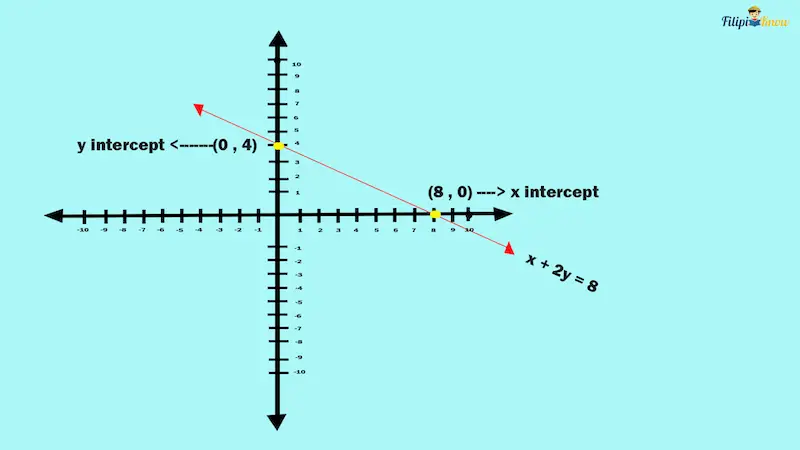
In our previous example above, we calculated the x-intercept and y-intercept of the line x + 2y = 8 as (8, 0) and (0, 4), respectively. Using the same example, we can plot the x and y intercepts of the line x + 2y = 8 in the coordinate plane and connect them using a straight line.

That’s it! We have just graphed x + 2y = 8 using its intercepts.

Let us use another example.

Example: Graph the line 2x + 5y = 10 using its intercepts.

Solution: Let us start by solving for the x and y-intercepts:

The computation above shows that the intercepts are (5, 0) and (0, 2).

We then plot these intercepts in the coordinate plane and connect them to form a straight line:

The Slope of a Line

You’ve learned from the previous section how to graph a line in a coordinate plane. This time, let us describe the steepness and direction of the line using its slope.

The slope of a line (or a linear equation) tells us the direction and steepness of the line. Let’s use the previous linear equation x + 2y = 8 as an example:

Based on the graph shown above, we can state that the graph of the line x + 2y = 8  is rising to the left. 

In this case, we can easily describe the direction of the line since we have already drawn its graph. But what if you are only given two points of the line or a linear equation? Can you describe the direction of its graph without actually graphing it in the plane?

Yes, if you know how to compute the slope of the line, you can determine the line’s direction without graphing it.

How To Determine the Slope of the Line Given Two of Its Points

If two points of the line are given, we can determine its slope using the formula:

Where:

•  y₁ is the ordinate of the first coordinate, and y₂ is the ordinate of the second coordinate.
• x₁ is the abscissa of the first coordinate, and x₂ is the abscissa of the second coordinate.

We use the letter m in this reviewer to represent the slope of the line.

When determining the slope of a line, remember the following:

• If the value of m is positive (i.e., m > 0): This means that the graph of the line is rising to the right.
• If the value of m is negative (i.e., m < 0): This means that the graph of the line is rising to the left.
• If the value of m is zero (i.e., m = 0): This means that the graph of the line is horizontal.
• If the value of m is undefined (this happens when the denominator turns out to be zero), the line’s graph is vertical.
• The larger the absolute value of m, the steeper the line is.

Let us have some examples.

Example 1: What is the slope of the line containing the points (1, 2) and (3, 5)?

Solution:

We have y₁ = 2, y₂ = 5, x₁ = 1, and x₂ = 3.

Using the slope formula:

Therefore, the slope is 3/2. 

Note that 3/2 is positive. This means that the graph of the line will rise to the right. You may try to graph the line using the given points and verify that the line is indeed rising to the right.

Example 2: Compute the slope of the line containing the points (-1, 5) and (0, 1).

Solution:

We have y₁ = 5 , x₁ = -1, y₂ = 1, and x₂ = 0

Using the slope formula:

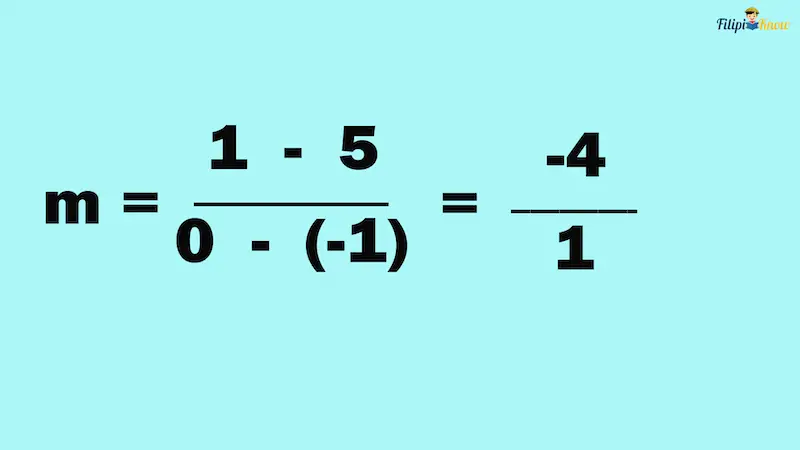
Therefore, the slope is -4/1 or -4.

Since we have a negative slope, this implies that the graph of the line will rise to the left.

Example 3: Compute the slope of the line containing the points (5, 1) and (5, 5).

Solution:

Using the slope formula:

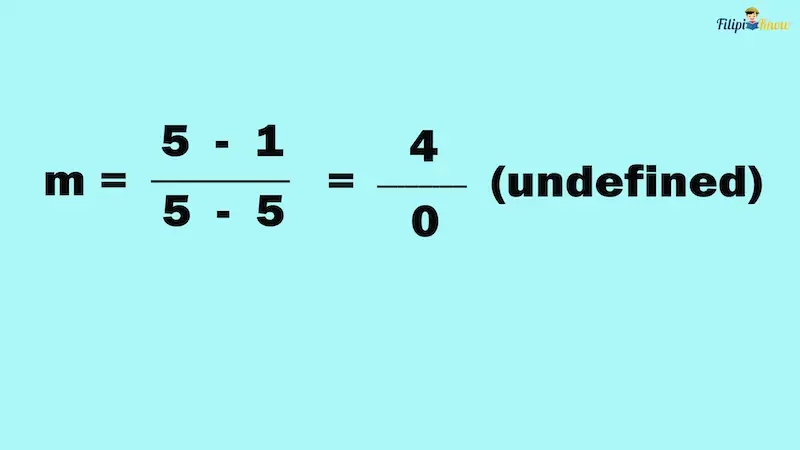
Since the slope we have computed is undefined, the graph of the line will be a vertical line.

Note: If the given points of the line have the same abscissa or first coordinate, the graph of that line is a vertical line, and its slope is undefined. On the other hand, if the given points have the same ordinate or second coordinate, the graph of that line is a horizontal line, and its slope is 0.

Example 4: Identify the slope of the line that contains the points (3, 4) and (7, 4).

Solution: Notice that the given points of the line have the same ordinate or second coordinate (both are 4). This implies that the slope of the line containing these points equals 0.

To verify, let’s use the slope formula:

Here, we have x₁ = 3, x₂ = 7, y₁ = 4, and y₂ = 4.

Substituting these values in the slope formula:

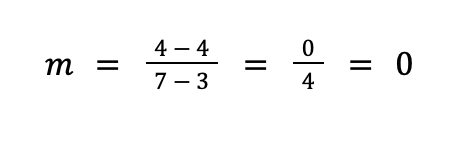
Indeed, the slope of the line in the given problem is 0. 

How To Determine the Slope of a Linear Equation

If the given problem is a linear equation, we can determine its slope by writing it in its slope-intercept form (i.e., y = mx + b), where m is the slope and b is the y-intercept of the line.

To write a linear equation in its slope-intercept form, we isolate y from other quantities. Afterward, we take the numerical coefficient of the x term. The numerical coefficient is the slope of that linear equation.

Example 1: Determine the slope of the linear equation 2x + y = 10.

Solution:

The first step is to isolate y from other quantities. This means that y should be the only variable on the left-hand side of the equation. This is possible by transposing 2x to the right-hand side of the equation:

2x + y = 10

y = -2x + 10 Transposing 2x to the right-hand side

By having y as the only quantity remaining on the left-hand side, we can successfully write the equation in its slope-intercept form. For the given equation, y = -2x + 10 is its slope-intercept form.

To find the slope, we take the coefficient of the x term in the slope-intercept form of the given equation. The x term in y = -2x + 10 is -2x, and the numerical coefficient is –2.

Therefore the slope is -2 or m = -2.

Since the slope is negative, it is expected that if we graph 2x + y = 10 in the coordinate plane, the graph will be a line rising to the left.

Example 2: What is the slope of the linear equation 3x – y = 11?

Solution:

We start by isolating y from other quantities by transposing 3x to the right-hand side of the equation:

We have now written the given linear equation in its slope-intercept form. Now, we can take the numerical coefficient of the x term, which would be our line’s slope.

Since the x term of y = 3x – 11 is 3x, and its numerical coefficient is 3, our slope must be 3.

Thus, the slope of the given linear equation is 3.

Now that you’ve learned the slope and how to determine the slope of a linear equation, let us explore its other mathematical uses. In the next section, we will explore what it means when two lines have the same or equal slopes or when two lines have negative reciprocal slopes.

 

Parallel and Perpendicular Lines in the Coordinate Plane

1. Parallel Lines in the Coordinate Plane

Suppose you have two linear equations with the same slope. What will these lines look like?

If two linear equations have the same slope, then the graph of these lines will show parallel lines.

Let us first define what parallel lines are. In geometry, parallel lines are lines that do not intersect. Even if you extend them infinitely in length, these lines will never cross each other. In other words, parallel lines will never meet forever.

If you have two linear equations with the same or equal slope, the graph of these linear equations in the coordinate plane will never meet or intersect.

Suppose we have two linear equations, x + 3y = 6 and x + 3y = 12.

First, let us transform both of these equations into their slope-intercept form so we can determine their respective slopes:

x + 3y = 6

3y = -x + 6 Transposing x to the right-hand side

y = -⅓x + 6 Dividing both sides by 3

Slope is -⅓

x + 3y = 12

3y = -x + 12 Transposing x to the right-hand side

y = -⅓x + 12 Dividing both sides by 3

Slope is -⅓

Based on our computations above, the linear equations x + 3y = 6 and x + 3y = 12 have the same or equal slopes (which is -⅓).

Since these linear equations have the same slope, their graphs are parallel lines or lines that will not intersect.

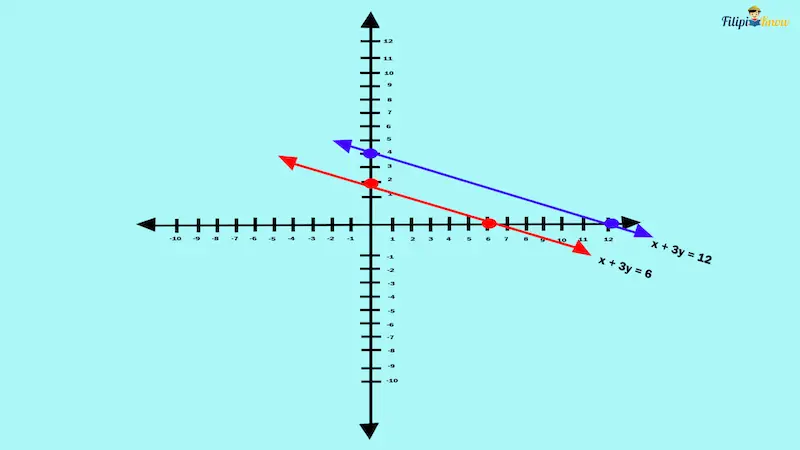
Indeed, the graphs of the linear equations x + 3y = 6 and x + 3y = 12 are parallel lines, as shown in our illustration above.

Again, if two lines have the same or equal slopes, then the lines are parallel.

Sample Problem: The equation of line A is x – 2y = 10. On the other hand, the slope of line B is (k + 1)x + y = 15. What must be the value of k so that the lines A and B are parallel?

Solution:

Lines A and B will be parallel if their slopes are equal. 

Let us take the respective slopes of each line.

Computing for the slope of line A:

x – 2y = 10

y = ½x – 5

Thus, the slope of Line A is ½.

Computing for the slope of line B:

(k + 1)x + y = 15

y = -(k + 1)x + 15

Thus, the slope of line B is -(k + 1).

Now, the slope of lines A and B must be equal. Hence, we have the following:

½ = -(k + 1)

We can express the equation above as:

½ = -k – 1 Using the distributive property

Let us now solve for the value of k:

½ = -k – 1

2(½ ) = 2(-k – 1) Multiplying both sides of the equation by the LCD (which is 2)

1 = 2(-k – 1)

1 = -2k – 2 Distributive property

2k = -1 – 2 Transposition method

2k = -3

k = -3/2 Division property of equality

Therefore, the value of k must be -3/2 

2. Perpendicular Lines in the Coordinate Plane

If two linear equations have slopes that are negative reciprocal of each other, then the graph of these linear equations would show perpendicular lines.

Here’s what perpendicular lines look like:

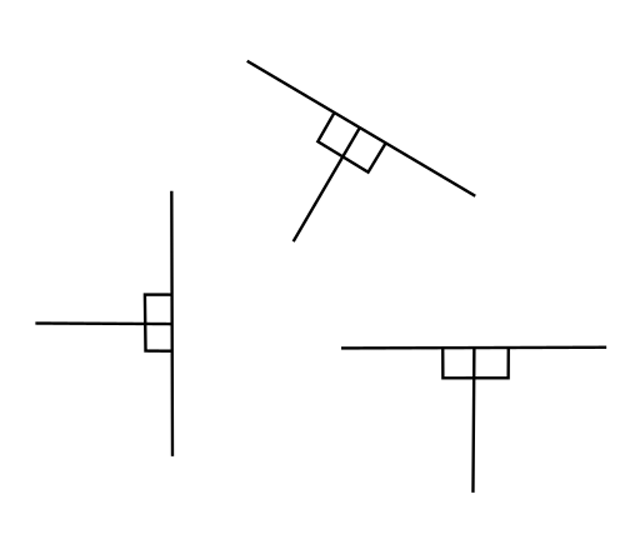
Two lines are perpendicular if they intersect and form 90-degree (or right) angles which look like a “T-shape” figure.

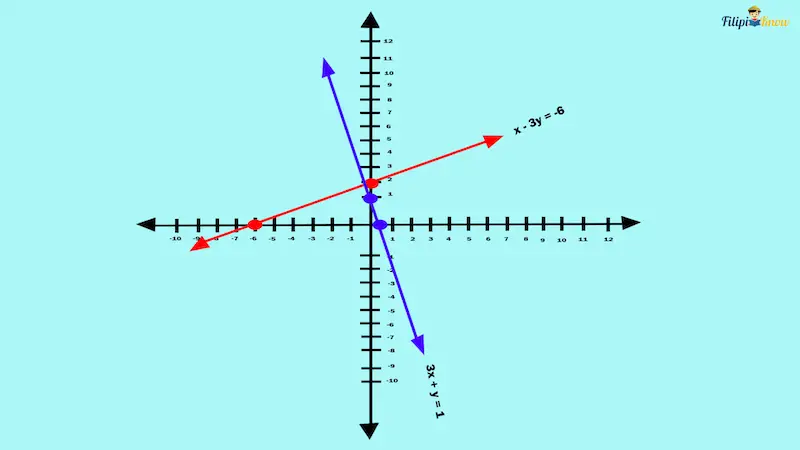
Suppose we have two linear equations, x – 3y = -6 and 3x + y = 1.

Let us first transform these equations into their slope-intercept form and then solve for their respective slopes:

x – 3y = -6

As we can see, the slope of the line x – 3y = -6 is ⅓.

3x + y = 1

y = -3x + 1 Transposing 3x to the right-hand side

As we can see, the slope of the line 3x + y = 1 is -3.

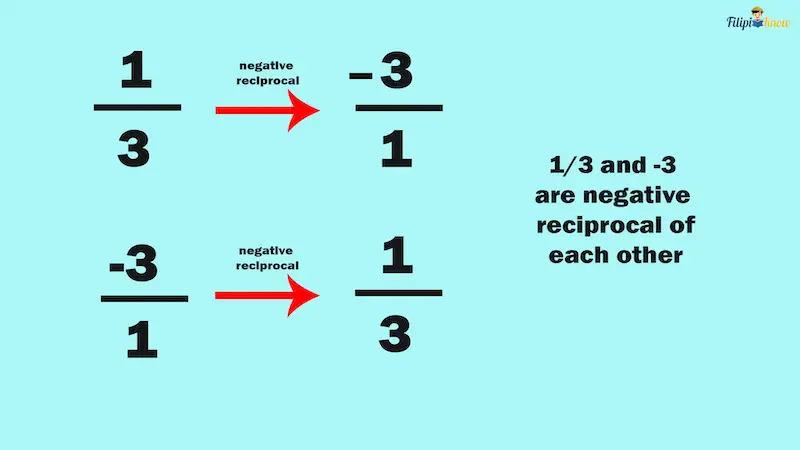
Notice that the slope of x – 3y = -6 is ⅓ while the slope of 3x + y = 1 is -3. ⅓ and -3 are negative reciprocals of each other.

Indeed, if we graph these equations in the coordinate plane, the lines are perpendicular to each other. 

Again, if two lines are perpendicular, then their slopes are negative reciprocal of each other.

Sample Problem: Line Z is perpendicular to a line whose equation is 3x – 5y = 15. Determine the slope of Line Z.

Solution:

Recall that if two lines are perpendicular, their slopes are negative reciprocals of each other.

Thus, the slope of line Z must be a negative reciprocal of the slope of 3x – 5y = 15.

Let us compute the slope of 3x – 5y = 15:

3x – 5y = 15

y = ⅗x – 3

As we can see, the slope of 3x – 5y = 15 is ⅗. The negative reciprocal of ⅗ is -5/3.

Thus, the slope of line Z is -5/3.

 

Graphs of Some Mathematical Functions in the Coordinate Plane

The previous module introduced you to basic mathematical functions, such as linear and quadratic functions. In this section, however, we’ll see what these functions will look like once we graph them in the coordinate plane. We will also explore the mathematical properties of their graphs.

1. Linear Functions in the Coordinate Plane

Recall that a linear function is a function in f(x) = mx + b form wherein the domain and range are the set of real numbers.

For instance, f(x) = ½x + 5 is an example of a linear function. Since  y = f(x), then we can rewrite f(x) = ½x + 5  as y = ½x + 5.

Notice that y = ½x + 5 is a linear equation in slope-intercept form. Therefore, we can state that f(x) = ½ x + 5 is also in the slope-intercept form. Furthermore, we can state that the slope of this function is ½, and its y-intercept is 5. 

From our discussion above, we can conclude that the graph of the function f(x) = ½x + 5 is a line with a slope of ½ and a y-intercept of 5.

Therefore, a linear function is a function wherein the graph is a line with a slope m and y-intercept b.

How To Graph a Linear Function by Plotting Two Points

Suppose you have a linear function. If you substitute or input a value of x into the function, the function will provide you a value for f(x) or y (since y = f(x)). Therefore, once you input a value of x, you will obtain a value of y, giving you a pair of values for x and y, making up a coordinate.

The points obtained through this method are what we are going to use to graph the linear function.

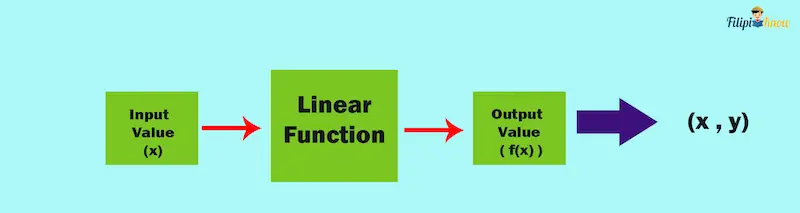
If we input a value of x into the function, we can obtain a value for f(x). Since f(x) = y, we can develop a coordinate (x, y).

Let us have some examples.

Example 1: Graph the linear function f(x) = ½ x + 5.

Solution: If we input a value of x into the function, we will obtain an output value for f(x). Since y = f(x) in a function, we can develop a coordinate (x, y). Note that we can input any real number value for x since the domain of a linear function is the set of real numbers.

Let us try to input x = 2:

f(x) = ½ x + 5

f(2) = ½ (2) + 5 We input x = 2 to the function

f(2) = 1 + 5

f(2) = 6

At x = 2, the value of f(x) is 6. Since, y = f(x), then y = 6. Therefore, we have two values: x = 2 and y = 6. This means that we have the coordinate (2, 6).

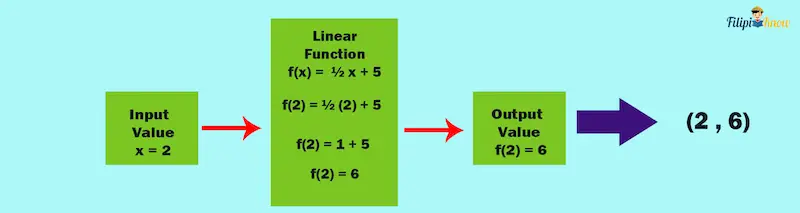
We already have one coordinate for f(x) = ½ x + 5. Now, let us look for another coordinate by inputting another value of x into the function.

Let us try to input x = 4:

f(x) = ½ x + 5

f(4) = ½ (4) + 5 We input x = 4 to the function

f(4) = 2 + 5

f(4) = 7

At x = 4, the value of f(x) is 7. Since y = f(x), then y = 7. Therefore, we have two values: x = 4 and y = 7. This means that we have the coordinate (4, 7).

Now, we have two coordinates: (2, 6) and (4, 7). We can finally plot these points in the coordinate plane and form a straight line. This straight line is the linear function f(x) = ½ x + 5.

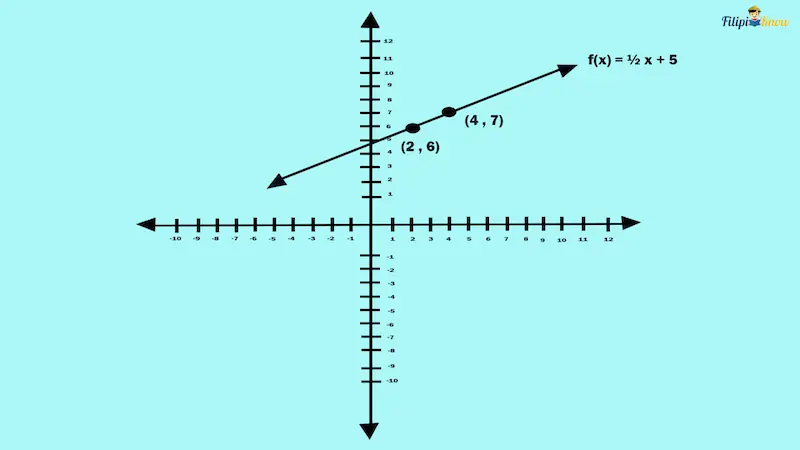
Example 2: The graph of the linear function f(x) = 3x – 9 passes through the points (3, a) and (b, 15). What are the values of a and b?

Solution: If f(x) = 3x – 9 passes through the point (3, a), then this means that if we input x = 3 to the function, we will obtain a value of f(x), which is equal to a. Thus, to find the value of a, we substitute x = 3 to the given linear function:

f(x) = 3x – 9

f(3) = 3(3) – 9 We input x = 3 to the function

f(3) = 9 – 9

f(3) = 0

Thus, the value of a must be 0. The point should be (3, 0).

On the other hand, if f(x) = 3x – 9 passes through the point (b, 15), then this means that if we input x = b to the function, we will obtain a value of f(x) which is equal to 15. Thus, to find the value of b, we substitute x = b and f(x) = 15 to the given linear function.

f(x) = 3x – 9

15 = 3b – 9 We substitute f(x) = 15 and x = b.

-3b = -15 – 9 Transposition method

-3b = -24

-3b⁄-3 = -24⁄-3 Dividing both sides by -3

b = 8

Hence, the value of b must be 8, and the point should be (8, 15).

 

2. Quadratic Functions in the Coordinate Plane

To recall, quadratic functions are functions wherein the highest exponent of the variable is 2. It is in the form f(x) = ax² + bx + c where a, b, and c are real numbers, and a is not equal to 0. The form f(x) = ax² + bx + c is the general form of a quadratic function.

Also, recall that the domain of a quadratic function is the set of all real numbers while its range is defined as R = {y | y ≥ k} if a is positive or R = {y | y ≤ k} if a is negative such that

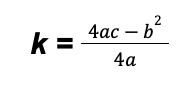
(k is the minimum value of the quadratic function when a > 0 while k is the maximum value of the quadratic function when a < 0).

When you graph a quadratic function in the coordinate plane, the shape of its graph will be a U-shaped or inverted U-shaped curve. This curve is known as the parabola. 

a. The Parabola and Its Properties

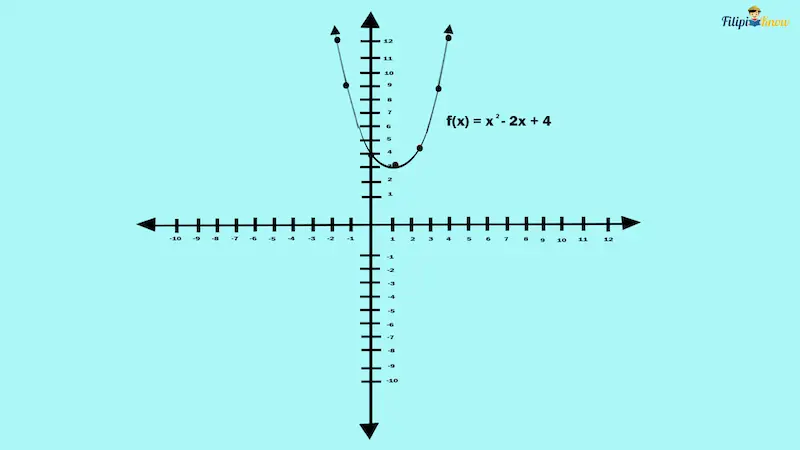
Let us take a look at the graph of f(x) = x² – 2x + 4 below:

i. Opening of the Parabola: Upward or Downward

The f(x) = x² – 2x + 4 graph is a parabola that opens upward (U-shaped). This upward opening of the graph is because the coefficient of the leading or quadratic term of the function is positive (a > 0). The leading term of f(x) = x² – 2x + 4 is x² and its coefficient is positive; thus, the parabola opens upward.

Remember, if the coefficient of the leading term of a quadratic function is positive (a > 0), then its graph is a parabola that opens upward. On the other hand, if the coefficient of the leading term of a quadratic function is negative (a < 0), then its graph is a parabola that opens downward.

The table below summarizes our conclusion about the opening of a parabola.

Sign of the Coefficient of the Leading or Quadratic Term	Opening of the Graph
Positive (a > 0)	Upward
Negative (a < 0)	Downward

Example: Determine whether the graph of the function f(x) = x – 3x – x² opens upward or downward.

Solution: The leading term of the given quadratic function is -x² and the sign of its coefficient is negative. Thus, its graph opens downward.

ii. The Vertex of a Parabola

Take a closer look at the f(x) = x² – 2x + 4 graph. Can you see the red-colored point of the graph? That point is (1, 3) and apparently the parabola’s extreme or lowest point. The extreme point of the parabola is called its vertex.

The vertex of the parabola is either the highest or lowest point of parabola. If the parabola opens upward, then the vertex is the lowest point. On the other hand, if the parabola opens downward, then the vertex is the highest point.

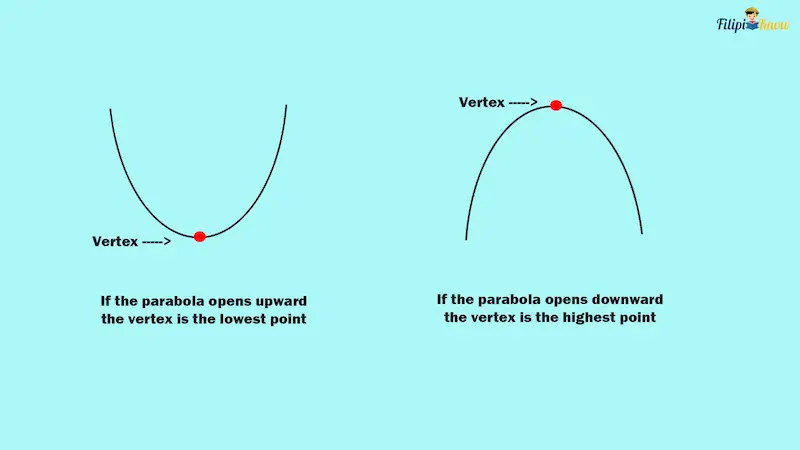
Going back to f(x) = x² – 2x + 4. Since its graph is a parabola that opens upward, its vertex is its lowest point. By contrast, the vertex of the function f(x) = -x² + 5x – 6 is its highest point since its graph is a parabola that opens downward.

The vertex’s ordinate (or y-coordinate) also tells us the maximum or minimum value of the function. For instance, the vertex of f(x) = x² – 2x + 4 is (1, 3). The ordinate (or y-coordinate) of (1, 3) is 3.

Since the vertex of f(x) = x² – 2x + 4 is its lowest point, then it means that 3 is the minimum or smallest value of the function f(x) = x² – 2x + 4. This implies that whatever number you input for x in the function, the result you will obtain will always be greater than or equal to 3. 

Look again at the f(x) = x² – 2x + 4 graph. You can verify from that graph that all values of y of the function are greater than or equal to 3. The function will never attain a value that is less than 3 since 3 is the minimum value of the function.

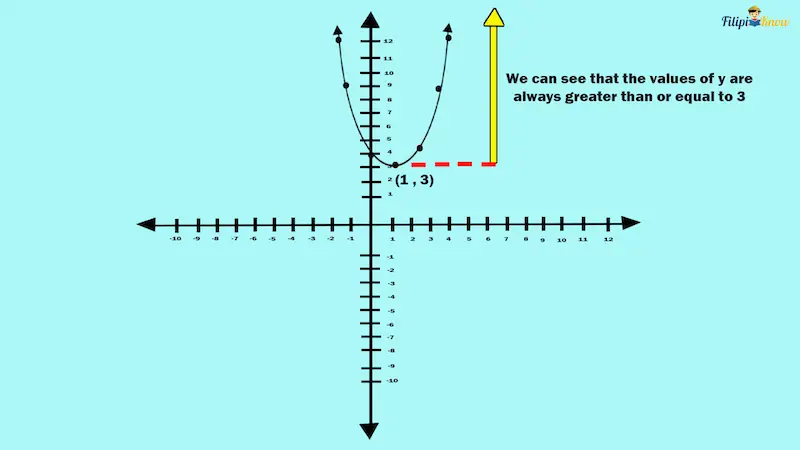
In other words, if the parabola opens upward, the y-coordinate of its vertex is the minimum value of the function. Meanwhile, if the parabola opens downward, the y-coordinate of its vertex is the maximum value of the function.

Example: The vertex of the function f(x) = -x² – 2x + 4 is (-1, 5). Determine the minimum or maximum value of the function.

Solution: The given function has a leading term that is negative. This means that its graph is a parabola that opens downward. This implies that the y-coordinate of its vertex is the maximum value of the function.

The y-coordinate of the vertex of the function f(x) = -x² – 2x + 4 is 5. This means that the maximum value of the function is 5.

This implies that the value of the function, whatever you will substitute for x, will never exceed 5.

How To Determine the Vertex of a Parabola

There are two ways to find the vertex of a parabola:

Method 1: Calculate the vertex using the formulas for its coordinates. If the given quadratic function is in general form, we can calculate its vertex using the formula below:

We use h to refer to the x coordinate of the vertex while k to refer to the y coordinate of the vertex.

If the k in the formula looks familiar, that’s because it’s the same thing we use to determine the range of the quadratic function. The y-coordinate of the vertex tells us the maximum or minimum value of the function. It sets the boundary for which y values are included in the function.

Example: Determine the vertex of f(x) = x² – 2x + 4 using the formula for the coordinates of the vertex.

The vertex of the parabola is (1, 3).

We can also identify the range of f(x) = x² – 2x + 4 from the vertex.

Based on the computation above, we have obtained k = 3. Since the function has a positive leading term, then the range of the function is the set of all real numbers greater than or equal to 3 or R = {y | y ≥ 3}.

Method 2: Using the vertex form of a quadratic function

We can transform a quadratic function in general form into its vertex form to obtain its vertex. The vertex form of a quadratic function is shown below:

For instance, f(x) = (x – 1)² + 3 is a quadratic function in vertex form. We have h = 1 and k = 3. Thus, the vertex of this function is (1, 3).

f(x) = (x + 1)² – 10 is another example of a quadratic function in vertex form. We have h = -1 and k = -10. Thus, the vertex of this function is  (-1, -10). 

If the given quadratic function is in its vertex form, we can quickly identify the values of h and k, enabling us to determine the function’s vertex quickly. 

However, if the function is in general form, we must first transform it into its vertex form.

How To Transform a Quadratic Function in General Form Into Its Vertex Form.

We use the completing square method to transform a quadratic function in general form into its vertex form. Here’s how to do it:

1. Isolate the constant term from the terms with x variable.
2. Make the coefficient of the quadratic term equal to 1 by factoring.
3. Add to both sides of the equation the square of half of the coefficient of the linear term.
4. Express the perfect quadratic trinomial formed into a square of a binomial.
5. Isolate f(x) from other quantities.

Example: Transform the quadratic function f(x) = x² – 2x + 4 into its vertex form and determine its vertex.

Thus, the vertex form of the given quadratic function is f(x) = (x – 1)²  + 3.

iii. The Axis of Symmetry of a Parabola

The parabola’s axis of symmetry is a vertical line that divides the parabola into two mirror parts. 

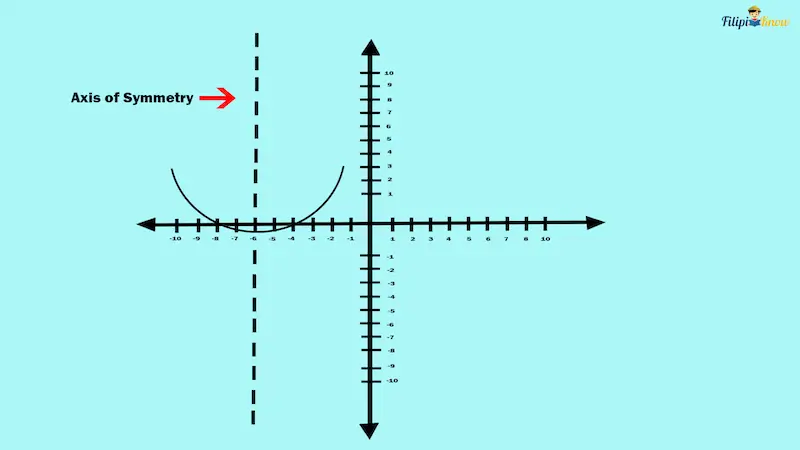
The axis of symmetry of a quadratic function is simply the vertical line that passes through h or the x-coordinate of the vertex.

Axis of Symmetry: line x = h or line x = -b⁄2a

Example: Determine the axis of symmetry of the quadratic function f(x) = -x² – 2x + 4.

Solution:

Using the formula for h of the vertex:

Therefore, the axis of symmetry of the given function is the line x = -1. 

iv. X-intercepts of the Parabola

The x-intercepts of a quadratic function are points in the graph of the quadratic function that touches the x-axis.

The x-intercepts of a quadratic function can be calculated if we set f(x) = 0 and then solve for the values of x. This means that the x-intercepts of the parabola are also the zeros of the quadratic function.

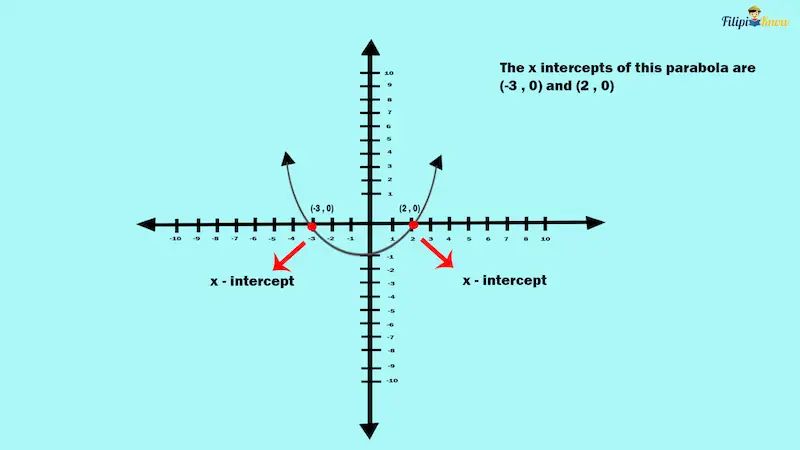
Example: Determine the x-intercepts of the graph of f(x) = x² – 7x + 6.

Solution:

Set f(x) = 0:

0 = x² – 7x + 6

We can rewrite the equation above using the symmetric property of equality:

x² – 7x + 6 = 0

We can solve the equation above by factoring:

x² – 7x + 6 = 0

(x – 6)(x – 1) = 0 By factoring

x – 6 = 0         x – 1 = 0 Equate each factor to 0

x₁ = 6 , x₂ = 1

The x-intercepts of the quadratic function are (6, 0) and (1, 0).

b. Graphing a Quadratic Function in the Coordinate Plane

Using the parabola properties we discussed above, we are now ready to graph a quadratic function. 

To graph a quadratic function, we first identify how the parabola will open. Then, we identify the vertex, x-intercepts, and other parabola points. Afterward, we’ll connect these points to create a parabola.

Example: Graph f(x) = x² – 7x + 6.

Solution: Since the coefficient of the leading term of the given quadratic function is positive, we expect that the graph of this function is a parabola that opens upward.

Now, let us determine the vertex of this function:

From our computation, the vertex of this parabola is (7/2, -25/4).

Meanwhile, the x-intercepts of this function were already calculated in our example above. We have obtained (6, 0) and (1, 0) as the x-intercepts.

We look for other points of the parabola by substituting some arbitrary values of x to the function:

From our computation above, we will use points (-1, 14) and (7, 6) to help us graph the functions.

Plot the vertex, x-intercepts, and other points of the parabola. Finally, connect them to form a parabola.

The parabola above is the graph of f(x) = x² – 7x + 6.

 

Circles in the Coordinate Plane

Aside from lines and parabolas, circles can also be analytically described in the coordinate plane. 

A circle is a geometric shape consisting of equidistant points or the same distance from a certain point. That point is called the center of the circle. On the other hand, the distance of the points in the circle from the center is called the radius.

Equation of a Circle

To graph a circle in the coordinate plane, there must be a corresponding equation describing that circle so that all points in the circle satisfy that equation.

If a circle has the origin as its center, the standard form of the equation of the circle is:

x² + y² = r² 

Where r is the radius of the circle.

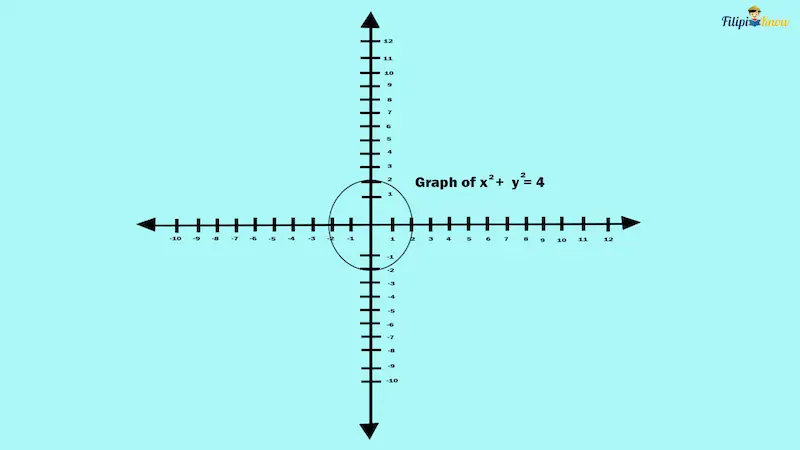
For instance, shown below is the graph of the circle x² + y² = 4. The center of this equation is at the origin or (0, 0), and its radius is equal to the square root of 4 (which is 2).

Example 1: Determine the center and radius of the circle x² + y² = 25.

Solution: The center of this circle is at (0, 0), and its radius is √25 = 5.

Example 2: What are the center and the radius of the circle x² + y² = 32?

Solution: The center of this circle is at (0, 0), and its radius is √32  or 4√2.

Meanwhile, if the center of the circle is not located in the origin and instead at a point in the coordinate plane, then the equation of the circle becomes:

(x – h)² + (y – k)² = r² 

Where h is the x-coordinate of the center,  k is the y-coordinate of the center, and r is the radius.

Example 1: What is the center of the circle (x – 8)² + (y – 1)² = 12?

Solution: We have h = 8 and k = 1. Thus, the center is (8, 1). On the other hand, the radius is √12 or 2√3.

Example 2: Determine the center and the radius of (x + 4)² + (y + 3)² = 49.

Solution: We have h = -4 and k = 3. Thus, the center is (-4, 3). On the other hand, the radius is √49  = 7.

Next topic: Sequence and Series

Previous topic: Functions

Return to the main article: The Ultimate Basic Math Reviewer

Download Printable Summary/Review Notes

Download Printable Flashcards

Test Yourself!

1. Practice Questions [Free PDF Download]

2. Answer Key [Free PDF Download]

3. Math Mock Exam + Answer Key