Patterns and rules surround us. 

For instance, the dry and wet seasons are alternating throughout the year; the stripes in the petals of a flower are arranged systematically; funds in a regular savings account earn interest monthly, and even your daily morning routine follows a well-defined pattern. 

Quantities and numbers also follow the rules and patterns. For instance, counting by 2s is one of the ways to define a pattern for numbers. 

This review will focus on sequence – a set of numbers following a certain pattern. Once we’ve unraveled its essential concepts, we will deal with series or the sum of these patterned numbers.

Click below to go to the main reviewer:

Ultimate UPCAT Reviewer

Ultimate NMAT Reviewer

Ultimate PMA Entrance Exam Reviewer

Ultimate LET Reviewer

What is a Sequence?

Look at this given set of numbers:

5, 10, 15, 20, 25, 30, ____.

What number must be placed in the blank? 

Yes, it should be 35.

It’s pretty easy to guess the missing number. By observing the numbers above, you can deduce that the next number can be obtained by adding 5 to 30. I’m sure you can do this because you know that the numbers follow a particular pattern (i.e., adding 5 to the previous number to get the next one). 

The numbers above (5, 10, 15, 20, 25, 30, 35) exemplify a sequence.  

A sequence of real numbers is an ordered list of real numbers. We will be most interested in sequences of numbers with a specific pattern. As we have mentioned earlier, the pattern of the sequence above is that it adds 5 to the previous number to get the succeeding one (5 + 5 = 10; 10 + 5 = 15; 15 + 5 = 20 …)

Sample Problem: What is the missing number in 72, 63, 54, 45, ______?

Solution: The sequence above follows a specific pattern. It subtracts 9 from the previous number to obtain the succeeding one (72 – 9 = 63; 63 – 9 = 54 …). Therefore, to get the missing number: 45 – 9 = 36. 

Hence, the answer is 36.

Terms of a Sequence

Each element in a sequence is called a term. Thus, in the sequence 5, 10, 15, 20, 25, 30, 35, each number is a sequence term. Moreover, 5 is the first term, 10 is the second term, 15 is the third term, and so on.

Notations in Sequence

Generally, the first term of a sequence can be expressed as a₁. The subscript “1” indicates that it is the first term of a particular sequence.

For example, in the sequence 5, 10, 15, 20, 25, 30, 35, the first term is 5. Therefore, a₁ = 5.

Now, if the first term of a sequence is expressed as a₁, the second term must be a₂, the third term must be a₃, the fourth term must be a₄, and so on. Thus, the nth term of a sequence is written as a_n. 

Hence, in general, a sequence can be written as:

a₁, a₂, a₃, a₄ …, a_n 

Sample Problem: Determine a₂ and a₃ of 2, 5, 8, 11, 14, 17.

Solution: a₂ and a₃ refer to the sequence’s second and third terms, respectively.  Since the second term of the sequence is 5 while the third term is 8, then a₂ = 5 and a₃ = 8. 

Rule of a Sequence

Please return to our first example: 5, 10, 15, 20, 25, 30, 35,… 

We have mentioned earlier that the pattern or rule of this sequence is that it adds 5 to a previous term to obtain the next one:

Using a formula or an equation, we can provide a more precise description of the sequence rule.

For instance, the rule of the sequence 5, 10, 15, 20, 25, 30, 35 can be expressed as a_n = 5n where a_n is the nth term of the sequence. Note that the nth term means any term of the given sequence. 

If we let n = 1, then by substitution:  a₍₁₎ = 5(1) = 5. This means that the first term of the sequence defined by the rule a_n = 5n is 5. 

If n = 2, then a₍₂₎ = 5(2) = 10. This means that the second term of the sequence defined by the rule a_n = 5n is 10. 

Similarly, if n = 5, then a₍₅₎ = 5(5) = 25. This means that the fifth term of the sequence defined by the rule a_n = 5n is 25. 

Sample Problem 1: The sequence 5, 10, 15, 20, 25, 30, 35 is defined by the equation a_n = 5n. What is the 100th term of the sequence?

Solution: To find the 100th term of the sequence, which is defined by the equation a_n = 5n, we let n = 100:

a₁₀₀ = 5(100) = 500

Therefore, the 100th term of the sequence is 500. 

Sample Problem 2: A sequence is defined by the rule a_n = 7n – 1. What is the first term of this sequence? How about its 20th term?

Solution: To find the first term of the sequence defined by the rule a_n = 7n – 1, we let n = 1:

a₁ = 7(1) – 1 = 6

Therefore, the first term of the sequence is 6.

On the other hand, to find the 20th term, we let n = 20:

a₂₀ = 7(20) – 1 = 140 – 1 = 139

Thus, the 20th term of the sequence is 139.

Sample Problem 3: Given the sequence with a rule defined by the equation a_n = 5 – 2n, what is the 15th term?

Solution: To find the 15th term, we let n = 15:

a₁₅ = 5 – 2(15) = 5 – 30 = -25

Thus, the 15th term of the sequence is -25.

Types of Sequence

1. Arithmetic Sequence

An arithmetic sequence is a sequence wherein every succeeding term is obtained by adding a fixed number to the previous term. 

Our previous example (i.e., 5, 10, 15, 20, 25, 30, 35) is an example of an arithmetic sequence because its succeeding term is derived by adding a fixed number (5) to the previous term. 

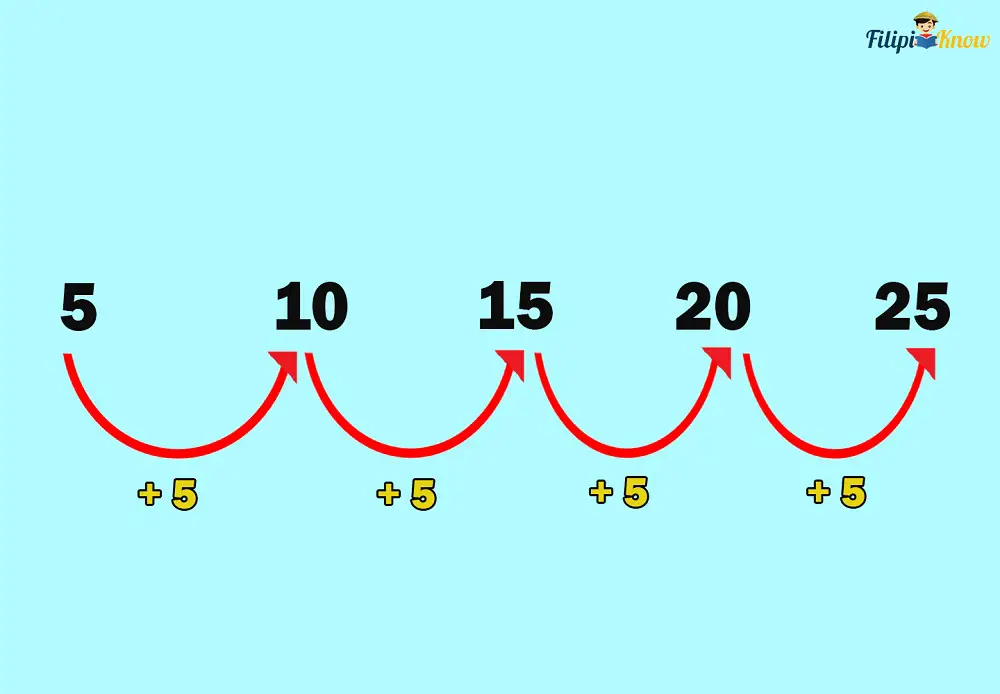
The common difference is the fixed number added to every term to get the succeeding one.

For instance, the sequence 5, 10, 15, 20, 25, 30, and 35 has a common difference of 5.

Sample Problem 1: Which of the following is/are arithmetic sequence(s)?

a. 8, 10, 12, 14, 16, 18,…

b. 15, 12, 9, 6, 3,…

c. 2, 4, 8, 16, 32, …

Solution:

a. Every succeeding sequence term is obtained by adding 2 to the previous term. 

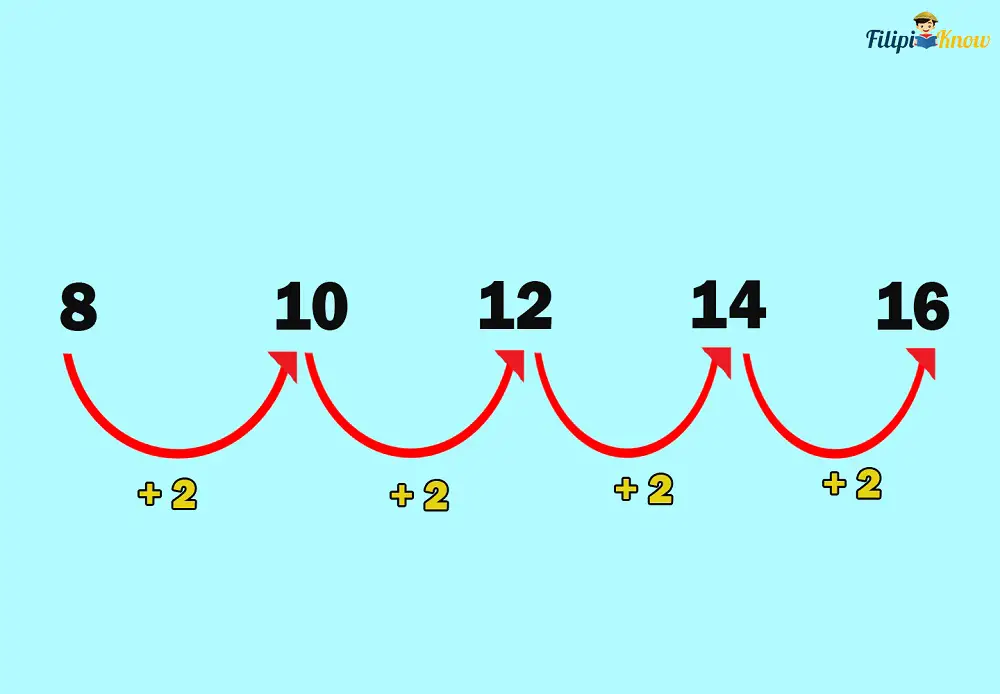
Therefore, this sequence is an arithmetic sequence with a common difference of 2.

b. This sequence works this way: subtracting 3 from the previous term to obtain the next one. Subtracting 3 from a number also means adding -3 to a number. 

Since we are still adding a fixed number (-3) to every term in the sequence, this is an arithmetic sequence. Thus, this is an example of an arithmetic sequence with a common difference of -3.

c. This is not an arithmetic sequence because the number added to each term to obtain the next one is not fixed or constant. 

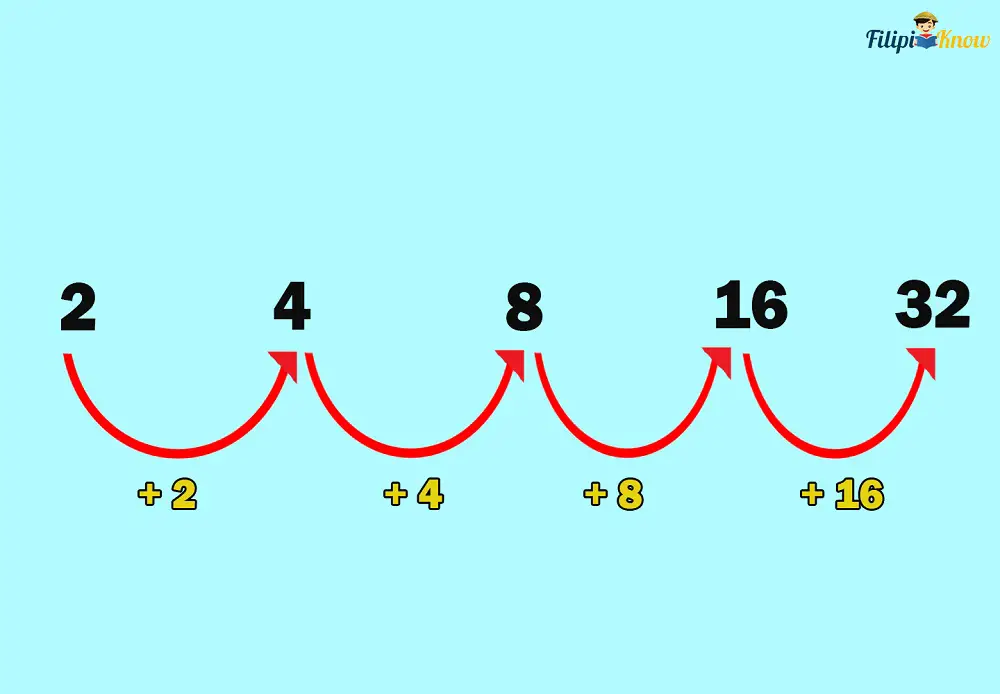
Therefore, only sequences in a and b are arithmetic. 

Sample Problem 2: Determine the common difference of the following arithmetic sequence.

a. 11, 22, 33, 44, 55,…

b. -8, -5, -2, 1, 4,…

c. ⅔, 1, 4/3, 5/3,…

Solution: To find the common difference (d) of an arithmetic sequence, we pick any term in the given sequence and subtract from it the term that precedes it. Mathematically,

d  = a_n – a_{n – 1}

Where d is a common difference, a_n is any term of the sequence (nth term), and a_{n – 1} is the term that precedes a_n. 

a. To identify the common difference in this arithmetic sequence, we can subtract from any of its terms the term that precedes it

Let’s try 33; the term preceding it is 22. Hence, the common difference is: 

d = 33 – 22 = 11

We can still get a common difference if we try another term. Let’s try 44; the term preceding it is 33:

d = 44 – 33 = 11

Hence, the common difference is 11.

b. Using the same method we used in the previous item, we can pick any term and subtract from it the term preceding it:

d = -2 – (-5) = -2 + 5 = 3

Hence, the common difference is 3.

c. To find the common difference, we pick any term and subtract from it the term that precedes it:

d = 5/3 – 4/3 = ⅓ 

Therefore, the common difference is ⅓. 

Finding the nth Term of an Arithmetic Sequence

Suppose we have this arithmetic sequence: 6, 9, 12, 15, 18,… and want to find its 25th term. What will you do to find this term?

If you’re planning to add 3 to each previous term until you reach the 25th term, then you’ll waste a lot of your precious time. Perhaps you’re good at arithmetic and can reach the 25th term in a few seconds. However, what if you’re looking for the 100th, 250th, or 500th term? Enumerating the terms one by one becomes inconvenient and time-consuming in this case. 

Luckily, mathematicians have done the heavy work and given us a general formula that we can use to find any term of an arithmetic sequence without listing each term manually. This formula is presented in the image below:

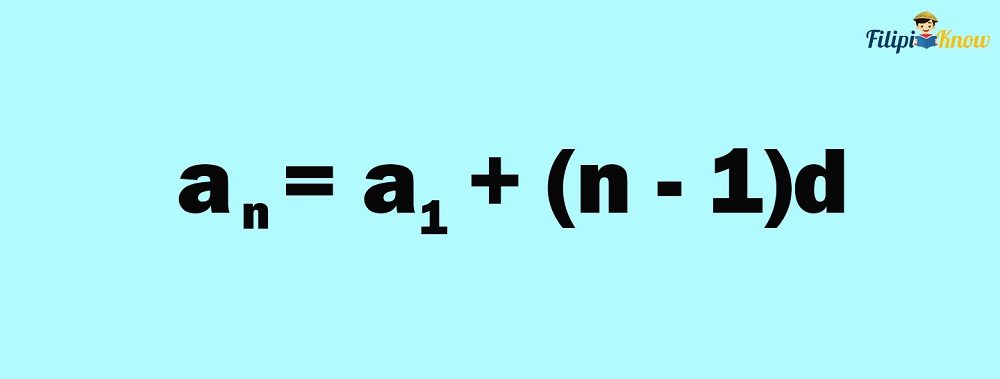
Here is the meaning of the variables in the formula above

• a_n is any term of the sequence; this is the term you’re looking for
• a₁ is the first term of the given sequence
• n is the number of the term you’re looking for (e.g., if you’re looking for the 25th term, then n = 25). If the last term of an arithmetic sequence is specified, n also represents the total number of terms in the sequence.
• d is the common difference of the arithmetic sequence

We will not discuss how this formula is derived because it’s quite long and complex. 

For now, let’s answer some examples to understand better how to use this formula.

Sample Problem 1: Determine the 25th term of the sequence 6, 9, 12, 15, 18,…

Solution: The formula to find any term of an arithmetic sequence is defined as:

a_n = a₁ + (n – 1)d

• The first term of the sequence is 6, so we have a₁ = 6
• Since we are looking for the 25th term, then we have n = 25
• The common difference (d) of the given sequence is 3 (e.g., 9 – 6 = 3)

Substituting the values we have derived:

a_n = a₁ + (n – 1)d

a₂₅ = 6 + (25 – 1)3

a₂₅ = 6 + (24)3

a₂₅ = 6 + 72

a₂₅ = 78

Thus, the 25th term of the sequence is 78.

Let us verify if the formula works by listing each term of the given sequence manually until the 25th term:

6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78

The list above shows that 78 is the 25th term of the given sequence. 

Sample Problem 2: Identify the 54th term of the sequence 17, 28, 39, 40, 51, 62,…

Solution: The formula to find any term of an arithmetic sequence is defined as:

a_n = a₁ + (n – 1)d

• The first term of the sequence is 17, so we have a₁ = 17
• Since we are looking for the 54th term, then we have n = 54
• The common difference (d) of the given sequence is 11 (28 – 17 = 11)

Substituting the values we have derived:

a₅₄ = a₁ + (n – 1)d

a₅₄ = 17 + (54 – 1)11

a₅₄ = 17 + (53)11

a₅₄ = 17 + 583

a₅₄ = 600

Thus, the 54th term of the sequence is 600.

Sample Problem 3: Selena plans to save money for 30 days. On the first day, she saved ₱20. On the second day, she saved ₱22. On the third day, she saved ₱24. On the fourth day, she saved ₱26. How much will Selena save on the 30th day?

Solution: How Selena saves money follows an arithmetic sequence of

20, 22, 24, 26,… This sequence has a common difference of 2 (d = 22 – 20 = 2).

To find how much Selena will save on the 30th day, we need to find the 30th term of the given sequence. The formula to find any term of an arithmetic sequence is defined as:

a_n = a₁ + (n – 1)d

• The first term of the sequence is 20,  so we have a₁ = 20
• Since we are looking for the 30th term, we have n = 30
• The common difference (d) of the given sequence is 2

Substituting the values we have derived:

a₃₀ = a₁ + (n – 1)d

a₃₀ = 20 + (30 – 1)2

a₃₀ = 20 + (29)2

a₃₀ = 20 + 58

a₃₀ = 78

Thus, the 30th term of the sequence is 78; Selena will save ₱78 on the 30th day. 

Sample Problem 4: How many numbers from 1 to 100 are divisible by 4?

Solution: At first glance, the given problem seems unrelated to the concept of the arithmetic sequence. However, this problem is solvable by applying what we have learned about this type of sequence.

If a number is divisible by 4, it is also a multiple of 4. For instance, 16 is a multiple of 4, so it also means that it is also divisible by 4.

To identify the numbers that are multiple (and divisible) by four between 1 to 100, we count by 4s:

4, 8, 12, 16, 20, 24, …

Note that the list of numbers above is an arithmetic sequence with a common difference of 4.

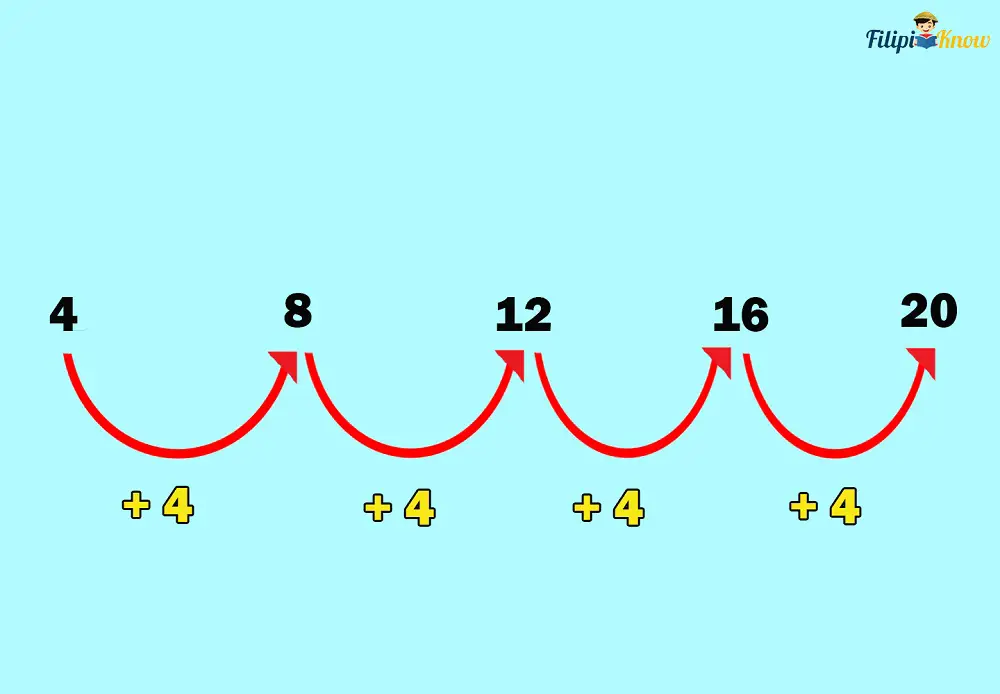
Thus, to find how many numbers from 1 – 100 are divisible by 4, we need to identify how many terms there are in the sequence.

However, we cannot identify the number of terms in the sequence without figuring out its last term. Note that the last number between 1 to 100 that is divisible by 4 is 96. This also means that the last term of our sequence should be 96.

Hence, the arithmetic sequence corresponding to all numbers between 1 to 100 divisible by 4 is 4, 8, 12, 16, 20, 24, …, 96. We can now identify how many terms there are in this sequence:

The formula for identifying any term of a given arithmetic sequence is

a_n = a₁ + (n – 1)d

However, this time we are not looking for a_n but n. Note that if the last term of a sequence is specified, then n may represent the total number of terms in a sequence. Since the sequence 4, 8, 12, 16, 20, 24, …, 96 ends with 96, we have a sequence with a specified last term. So, n in this problem serves as the total number of terms in the sequence (the total number of numbers from 1 – 100 that are divisible by 4). 

• Since 4 is the first number in the sequence, then we have a₁ = 4
• Since we are interested in finding the number of terms in 4, 8, 12, 16, 20, …, 96 or the value of “n,” the value of a_n should be the last term which is 96. 
• The common difference (d) is 4 

Substituting these values in the formula, we can now solve for n:

a_n = a₁ + (n – 1)d

96 = 4 + (n – 1)4

Let us now do some algebra to solve the value of n:

96 = 4 + (n – 1)4
96 = 4 + 4n – 4	Distributive Property
96 = 4n	Combining like terms
96/4 = 4n/4	Dividing both sides of the equation by 4
24 = n
n = 24

Since n represents the number of terms in the sequence 4, 8, 12, 16, 20, 24, … 96, there are 24 terms in this sequence. This also implies that 24 numbers between 1 to 100 are divisible by 4. 

Sample Problem 5: The first term of an arithmetic sequence is -9, while its 12th term is 1. What is the common difference between this arithmetic sequence?

Solution: We have a₁ = -9 since -9 is the first term of the sequence. On the other hand, a₁₂ (the a_n in this case) is 1. Furthermore, we have n = 12. Our goal is to solve for the common difference or d.

an = a1 + (n – 1)d
1 = -9 + (12 – 1)d	By substitution
1 = -9 + 11d
1 + 9 = 11d	Transposition method
10 = 11d
10/11 = 11d/11	Dividing both sides of the equation by 11
d = 10/11

Thus, the common difference in the sequence in this problem is 10/11.

2. Geometric Sequence

In an arithmetic sequence, there’s a fixed number added to each term to obtain the succeeding term (called the common difference). Meanwhile, a geometric sequence has each term multiplied by a fixed number to obtain the next one. 

Look at this sequence: 3, 6, 12, 24, 48, … 

Unlike in an arithmetic sequence, there is no common difference. Instead, each term is multiplied by 2 to obtain the next one. 

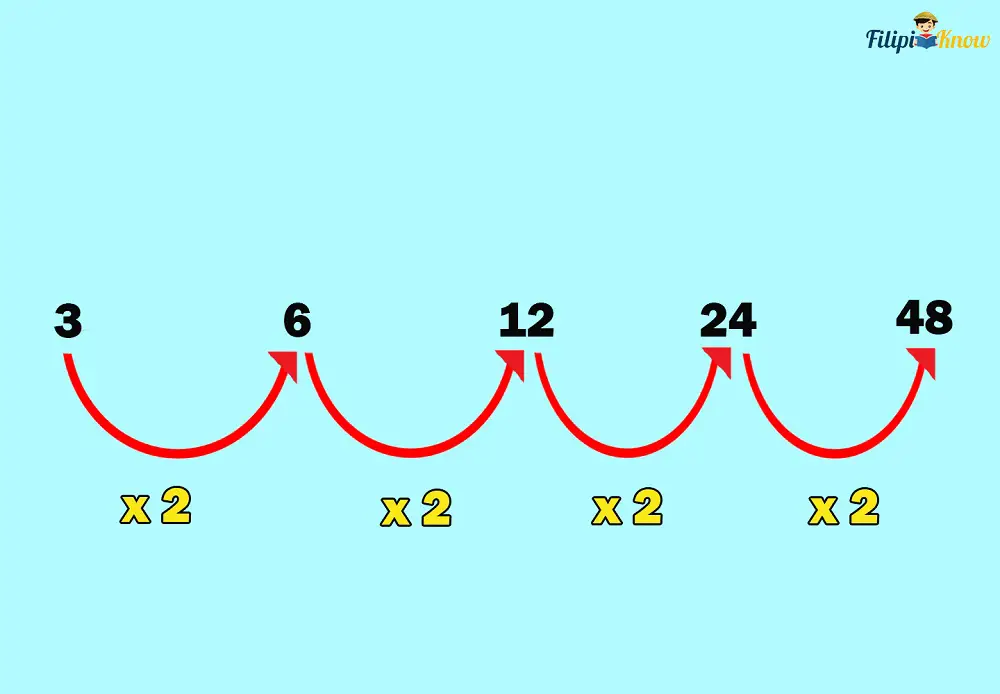
Since this sequence is characterized by multiplying a term by 2 to get the next one, this is an example of a geometric sequence. 

In a geometric sequence, each term is multiplied by a fixed number to get the next term; the fixed number is called the common ratio (denoted by the letter r).

This means that the common ratio of the sequence 3, 6, 12, 24, 48, … is 2.

Sample Problem 1: Which of the following is/are geometric sequence(s)?

a. 1, 4, 7, 10, 13, …

b. 2, 6, 18, 54, …

c. 9, 11, 14, 18, …

Solution:

a. This sequence has a common difference of 3. Thus, it is not a geometric sequence.

b. This sequence has a common ratio of 3. This means we multiply the previous term by 3 (e.g., 2 x 3 = 6; 6 x 3 = 18) to obtain the next term. Hence, this is a geometric sequence.

c. This sequence is neither arithmetic nor geometric sequence. It has no common difference or common ratio. 

Sample Problem 2: Identify the common ratio of the following sequence.

a. 1, 5, 25, 125, 625, …

b. 3, -6, 12, -24, 48, …

Solution:

Here’s a simple trick to identify the common ratio of a geometric sequence. Pick any term from the sequence, then divide it by the preceding term. Let us apply this trick to find the common ratio of the sequence:

a. Let us pick 25. The term that precedes it is 5. Hence, the common ratio is:

r = 25/5 = 5

b. Let us pick -24. The term that precedes it is 12. Thus, the common ratio is:

r = -24/12 = -2

Again, we can find the common ratio of a geometric sequence by picking any term from the sequence (except the first term), then dividing it by the term that precedes it. Mathematically,

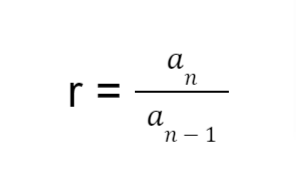
Where r is the common ratio, a_n is the nth term (any sequence term), and a_n-1 is the term that precedes a_n. 

Finding the nth Term of a Geometric Sequence

Like in an arithmetic sequence, we can also determine any term of a geometric sequence using a formula. Suppose we want to identify the 10th term of 3, 6, 12, 24, … we can use the formula below to find it without listing the terms.

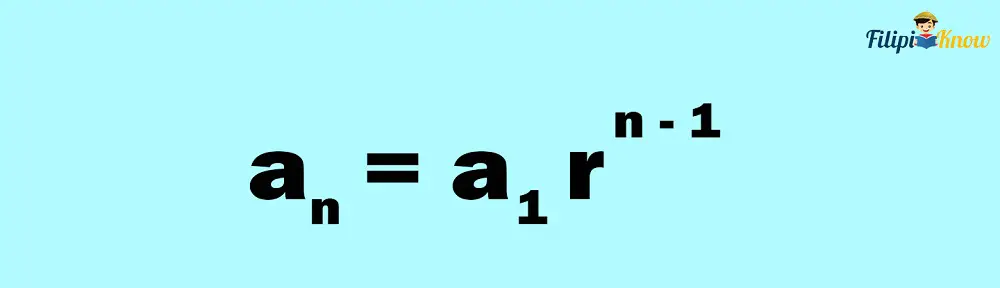
Where:

• a_n is any term of the sequence; this is the term you’re looking for
• a₁ is the first term of the given sequence
• n is the number of the term you’re looking for (For example, if you’re looking for the 25th term, n = 25)
• r is the common ratio of the geometric sequence

Sample Problem 1: Find the 10th term of the geometric sequence 3, 6, 12, 24, …

Solution: The first term of the sequence is 3. Thus, we have a₁ = 3. Since we are looking for the 10th term or a₁₀, we have n = 10. 

The common ratio of the sequence is r = 6/3 = 2. 

Using the formula for the nth term of a geometric sequence: a_n = a₁r^{n – 1}

an = a1rn – 1
a10 = 3(2)10-1	By substitution
a10 = 3(2)9
a10 = 3(512)	29 = 512
a10 = 1536

Therefore, the 10th term of the geometric sequence is 1,536.

Sample Problem 2: What is the 8th term of the geometric sequence 1/16, ⅛, ¼, ½, … 

Solution: The first term of the sequence is 1/16. Thus, we have a₁ = 1/16. Since we are looking for the 8th term or a₈, we have n = 8. 

The common ratio of the sequence is

You can review our module about how to divide fractions to learn how we can obtain the answer above. 

Using the formula for the nth term of a geometric sequence: a_n = a₁r^{n – 1}

an = a1rn – 1
a8 = 1/16(2)8-1	By substitution
a8 = 1/16(2)7
a8 = 1/16(128)	27 = 128
a8 = 128/16
a8 = 8

Therefore, the 8th term of the geometric sequence is 8.

3. Harmonic Sequence

Before discussing a harmonic sequence, look at this arithmetic sequence: 4, 7, 10, 13, 16, 19, … 

Let us take the reciprocal of each term of the arithmetic sequence above: 

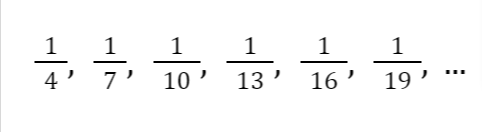
The set of fractions above is an example of a harmonic sequence. 

A harmonic sequence is derived from the reciprocals of the terms of an arithmetic sequence. This also means that the reciprocal of the terms of a harmonic sequence forms an arithmetic sequence. 

Going back to our example of a harmonic sequence above, taking the reciprocal of each term forms an arithmetic sequence with a common difference of 3:

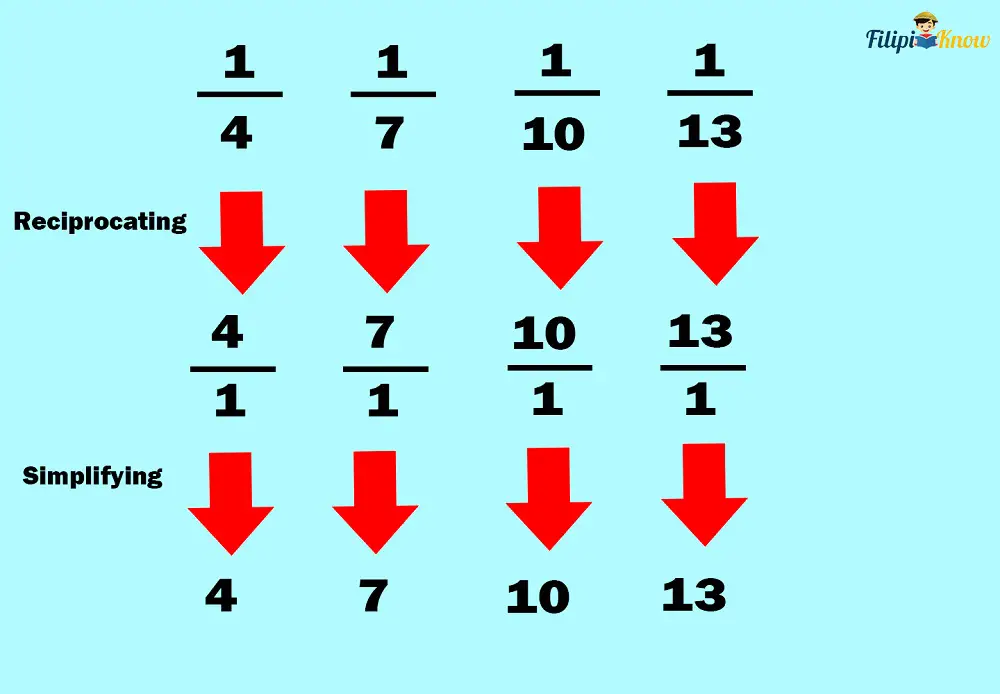
This type of sequence is called “harmonic” because it is said that ancient Greek mathematicians like Pythagoras used this particular type of numerical pattern to devise a “mathematical” theory that could explain musical harmony. 

Sample Problem: Is 1/9, 1/7, ⅕, ⅓, … a harmonic sequence?

Solution: If we take the reciprocal of each term of the sequence above, then:

9, 7, 5, 3, …

The sequence above is an arithmetic sequence because it has a common difference of -2. Therefore, the original sequence is a harmonic sequence. 

4. Fibonacci Sequence

A Fibonacci sequence is a sequence wherein the succeeding term is obtained by adding two previous terms. It’s named after Leonardo “Fibonacci” of Pisa, an Italian mathematician who first discussed it during the early 1200s. 

Here’s an example of a Fibonacci sequence: 1, 1, 2, 3, 5, 8, 13, …

In the sequence above, any term (except for the first and second terms) is obtained by adding two previous terms. For instance, to obtain 2, we add two terms preceding it which are 1 and 1 (i.e., 1 + 1 = 2). Similarly, to get 8, we add the two terms before it (i.e., 3 + 5 = 8).

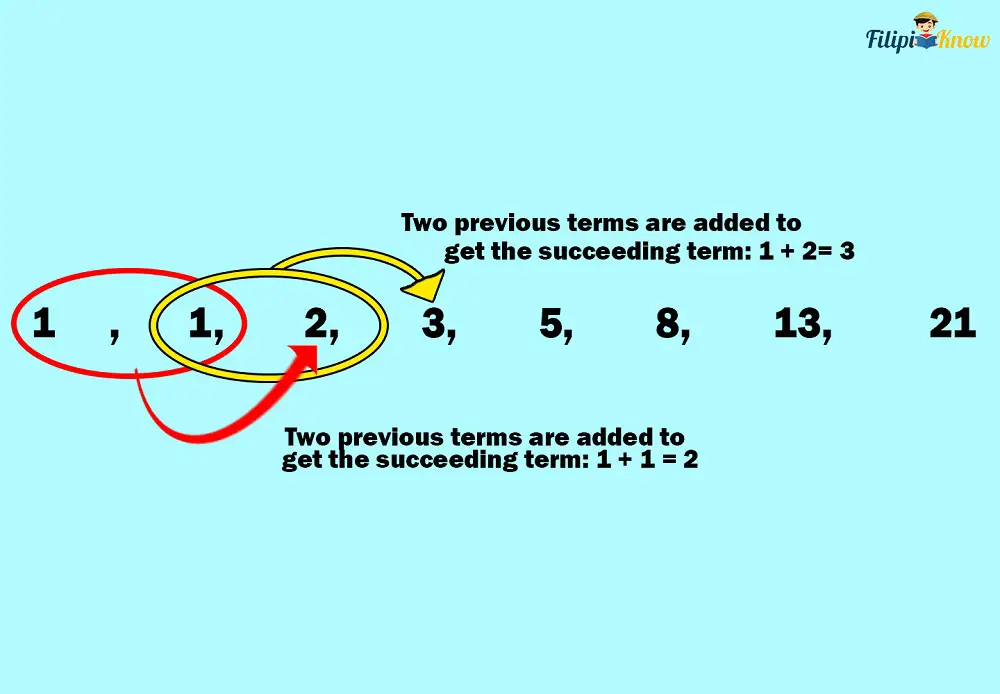
Therefore, the nth term of a Fibonacci sequence can be expressed mathematically as follows:

a_n = a_n-1 + a_{n – 2}

where a_n is any sequence term,  with a_{n – 1} and a_n-2 corresponding to the two terms that precede a_n. 

Sample Problem:  What is the missing number in this sequence: 3, 3, 6, 9, 15, 24, ____?

Solution: The sequence above is a Fibonacci sequence because each succeeding term is obtained by adding two previous terms.

Hence, we add 15 and 24: 15 + 24 = 39 to find the missing number.

Thus, the missing number is 39. 

What is a Series?

In mathematics, a series is a sum of all terms of a particular sequence. 

For instance, consider this sequence: 3, 5, 7, 9, 11, …

If we add all of the terms of the sequence above, then it becomes a series: 3 + 5 + 7 + 9 + 11 + …

Hence, if a₁, a₂, a₃, …, a_n represents the terms of a sequence, then a series S is defined as:

S = a₁ + a₂ + a₃ + … + a_n

Sample Problem: Transform the sequence -4, -2, 0, 2, 4, 6, … into a series.

Solution: To turn the sequence above into a series, we express it as a sum of its terms:

(-4) + (-2) + 0 + 2 + 4 + 6 + …

Finite Sum and Infinite Series

A mathematical series can be a finite or an infinite sum (series). 

For example, if we are just interested in adding the first ten terms of the sequence 3, 5, 7, 9, …., the series 3 + 5 + 7 + 9 … + 21 is a partial sum of the sequence (21 is the 10th term of the given sequence). 

Thus, a finite series refers to the sum of the first n terms of an arithmetic or geometric sequence.

On the other hand, if we are adding a limitless number of terms in a sequence, then we’re now dealing with an infinite series. For instance, adding all terms of the sequence 3, 5, 7, 9, … up to infinity is an example of an infinite series.

An infinite series is a series where an infinite number of terms of a sequence are added. 

You might find it ridiculous why someone would add the terms of a sequence like 3, 5, 7, 9, … up to infinity. We cannot estimate an exact sum because we are dealing with infinite addends. The sum will get larger and larger without reaching a definite end.

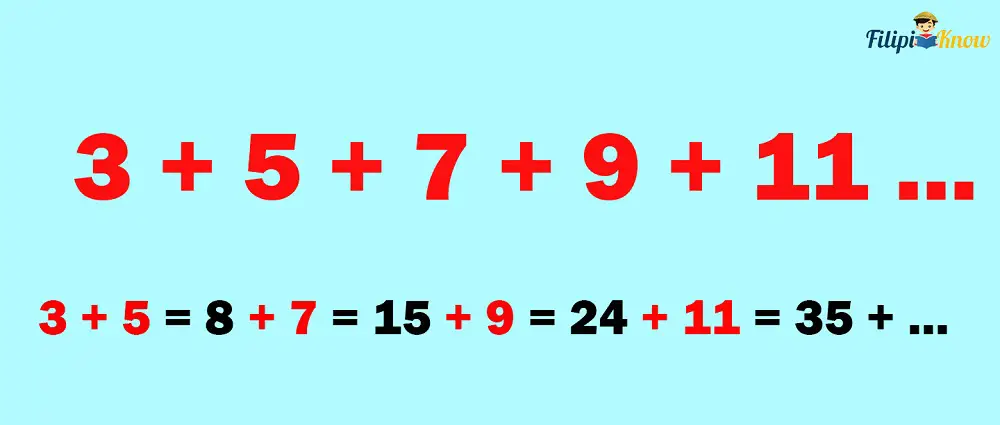
However, some infinite series “converge” to an exact result whether you believe it or not. That is,  it is possible to obtain an exact sum by adding an endless number of terms for some sequences. For instance, if you add all terms of the sequence ½, ¼, ⅛, 1/16, .. up to infinity, the sum will be 1.

I know this thing seems counterintuitive and mind-boggling. Don’t worry; we will shed light on this confusing thing later as we explain the type of infinite series with an “exact” sum.

Types of Series

1. Arithmetic Series

An arithmetic series is the sum of the terms in an arithmetic sequence. 

For instance, consider the arithmetic sequence: 4, 5, 7, 9, … 21. 

Let S be the sum of the terms of this arithmetic sequence. Therefore, we have 

S = 4 + 5 + 7 + 9 + … + 21

From here, we can see that S is an example of an arithmetic series. 

Note that an arithmetic series must have a definite number of terms. In other words, the addends must be finite. In our previous example, S = 4 + 5 + 7 + 9 + … + 21, we add the terms from 4 to 21. This allows us to have an “exact” value of S. 

If we don’t specify a definite number of terms, we add an infinite number. Suppose that instead of S = 4 + 5 + 7 + 9 + … + 21, we just write it as S₂ = 4 + 5 + 7 + 9 + … .

Since S₂ has no definite end, we’re adding an infinite number of terms, and the sum will be larger and larger without bounds. 

In short, an arithmetic series must have a definite number of addends.

So, to formally define an arithmetic series, we express it mathematically as follows:

S_n = a₁ + a₂ + a₃ + … + a_n

Such that a_1, a₂, a₃, …, a_n are terms of an arithmetic sequence and a_n represents the end of the sequence. 

Sample Problem: Which of the following is/are arithmetic serie(s)?

1. 7 + 11 + 16 + 22 + … + 320
2. 6 + 12 + 18 + 24 + … + 120
3. 9 + 8 + 7 + 6 + … + (-1)

Solution:

1. This is not an arithmetic series. Note that the addends do not satisfy the condition to become an arithmetic sequence because they have no common difference. 

• 11 – 7 = 4
• 16 – 11 = 5
• 22 – 16 = 6

2. This is an arithmetic series since the addends are terms of an arithmetic sequence with a common difference of 6.

3. This is an arithmetic series since the addends are terms of an arithmetic sequence with a common difference of -1.

Formula for the Sum of an Arithmetic Series

We can use two formulas depending on the given situation to find the sum of an arithmetic series.

Such that:

• a₁ is the first term
• n is the number of terms being added to the series
• a_n is the nth term of the sequence. If the sequence has a specified last term, then a_n is also the last term. 
• d is the common difference between the terms or addends in the series

We use the first formula when the sequence has no specified last term. For example, if we want to find the sum of the first 50 terms of 2 + 4 + 6 + 8 + …, then we use the first formula. On the other hand, the second formula is used when the last term of the sequence is specified. For example, we can use the second formula to compute the sum of 1 + 2 + 3 + … + 50.

It’s easy to derive the formulas above. However, we will not discuss this anymore because it is beyond the scope of our reviewer. 

Let us solve some sample questions to understand further how to use these formulas.

Sample Problem 1: What is the sum of all whole numbers from 1 to 100?

Solution: By writing the problem as a mathematical sentence, we’ll obtain the following:

1 + 2 + 3 + 4 + … + 100

It’s clear here that we are dealing with an arithmetic series since the terms have a common difference of 1. Since the sequence has a specified last term (which is 100), then it’s advisable to use the second formula: 

• Since the first term of the series is 1, we have a₁ = 1
• The last term of the series is 100, so a_n = 100
• There are 100 whole numbers from 1 to 100, so we have n = 100

Let us insert these values into the formula for the sum of an arithmetic series.

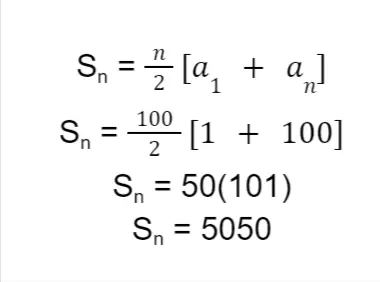
Therefore, the sum of numbers from 1 to 100 is 5050. If you have a lot of spare time, you can verify this manually by doing the addition process. 

Sample Problem 2: What is the sum of 4 + 6 + 8 + 10 + … + 32? 

Solution: Since the given arithmetic series above has a definite last term (which is 32), then we will use formula #2.

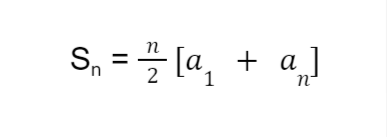
The first term of the given series is 4. So we have a₁ = 4. Meanwhile, the last term of the sequence is 32, so we have a_n = 32.

For the value of n, we need to determine the number of terms in the series 4 + 6 + 8 + 10 + … + 32. We can do this by returning to our formula for the nth term of an arithmetic sequence. You may manually count the number of terms if you don’t want to perform some algebra. 

Let us do the algebra stuff by using the formula:

a_n = a₁ + (n – 1)d

We have a₁ = 4, a_n = 32, and d = 2. Let us insert these values into the formula above and then solve for the value of n:

an = a1 + (n – 1)d
32 = 4 + (n – 1)2	By substitution
32 = 4 + 2n – 2	Distributive property
32 = 2 + 2n	Combining like terms
-2 + 32 = 2n	Transposition method
30 = 2n
30/2 = 2n/2	Dividing both sides by 2
n = 15

Since we have computed that n = 15, there are 15 terms from 4 to 32 in the series 4 + 6 + 8 + 10 + … + 32. 

Our variables for the formula to identify the sum of the arithmetic series are complete. 

We have a₁ = 4, a_n = 32, n = 15, and d = 2. Let us substitute these values in the formula:

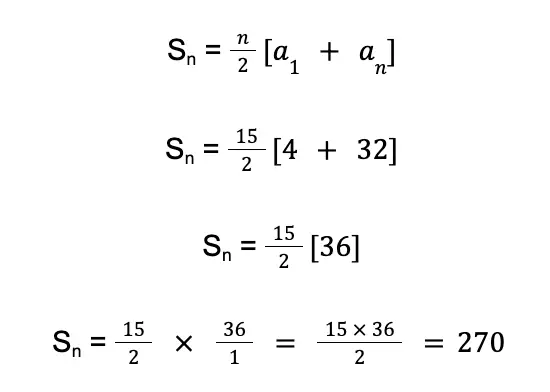
Hence, the sum of the arithmetic series 4 + 6 + 8 + 10 + … + 32 is 270.

Sample Problem 3: Bea saved ₱100 on February 1 in her savings account. On February 2, she saved ₱105. On February 3, she saved ₱110, and so on. How much money did Bea save at the end of February (assuming it is not a leap year)?

Solution: How Bea saved money during February follows an arithmetic sequence with a common difference of 5. 

• February 1 = 100
• February 2 = 105
• February 3 = 110

To determine the total amount of money that Bea saved for the entire month of February, add the daily amount of money saved:

Total amount that Bea saved in February = 100 + 105 + 110 + … 

The addition sentence above is an arithmetic series.  We shall use the first formula since the last term is not specified. 

Since 100 is the first term of the series, we have a₁ = 100

Note that we are looking for the total amount of money Bea saved in February. Since it is not a leap year, Bea saved money for 28 days. Therefore, we have n = 28.

Lastly, the common difference is 5. So we have d = 5.

Let us input these values into the formula for the sum of an arithmetic series.

Therefore, Bea saved a total amount of ₱4,690 for the entire month of February. 

2. Geometric Series

A geometric series is the sum of the terms of a geometric sequence. 

Consider this geometric sequence: 1, 3, 9, 27, … Suppose that S represents the sum of the terms of this sequence such that S = 1 + 3 + 9 + 27 + … Since S is the sum of the terms of a geometric sequence, then S is a geometric series.

Unlike with arithmetic series, the terms in a geometric series can be finite or infinite. A finite geometric series has a definite number of terms. This means that a finite geometric series has a “last” term.  It is also the sum of the first n terms of a geometric sequence.

For instance, the geometric series 2 + 4 + 8 + … + 256 is a finite geometric series because it has a definite number of terms. Note that there is the last term in this series which is 256. 

On the other hand, an infinite geometric series has an infinite number of terms being added. This means it has no “last” term because it has endless addends. 

However, not every infinite geometric series has an “exact” sum. For instance, the infinite geometric series 2 + 4 + 8 + 16 + … doesn’t have an exact sum. The sum that we will obtain will get larger and larger without bounds. 

An infinite geometric series will have an “exact” sum if it satisfies a special condition. That is, the absolute value of the common ratio (r) must be between 0 to 1:

0 < | r | < 1

For instance, the geometric series ½ + ¼ + ⅛ + … will have an “exact” sum since its common ratio is ½ (¼ ÷ ½ = ½). Note that the absolute value of ½ is between 0 to 1. 

Thus, in general, a finite geometric series can be expressed mathematically as:

S_n = a₁ + a₂ + a₃ + a₄ + … + a_n 

where a₁, a₂, a₃, …, a_n are terms of a geometric sequence and a_n is the “last” addend of the series.

If the absolute value of the common ratio of the terms is between 0 and 1 (0 < |r| < 1), then the infinite geometric series can be expressed as:

S = a₁ + a₂ + a₃ + a₄ + … 

where a₁, a₂, a₃, a₄, … are terms of a geometric sequence with no definite “last” term.  

Sample Problem 1: Which of the following is a geometric series?

a. 3 + (-6) + 12 + … + (-96)

b. 7 + 9 + 11 + … 25

c. 2 + 1 + 1/2 + …

Solution: The series in A and C are geometric series with a common ratio of -2 and ½, respectively. Meanwhile, the series in B is an arithmetic series with a common difference of 2. 

Sample Problem 2: Which of the following infinite geometric series satisfies the condition to have an exact sum?

a. 9 + 27 + 81 + …

b. -1 + 5 + (-25) + 125 + …

c. 16 + 4 + 1 + … 

Solution: A and B have a common ratio of 3 and -5, respectively. Note that the respective absolute values of these numbers don’t fall within the 0-1 range. Hence, they do not satisfy the condition of having an exact sum. On the other hand, the common ratio in C is ¼, which falls within the 0 -1 range. Therefore, this series will have an exact sum. 

Formula To Find the Sum of a Finite Geometric Series

Shown below is the formula for the sum of a finite geometric series:

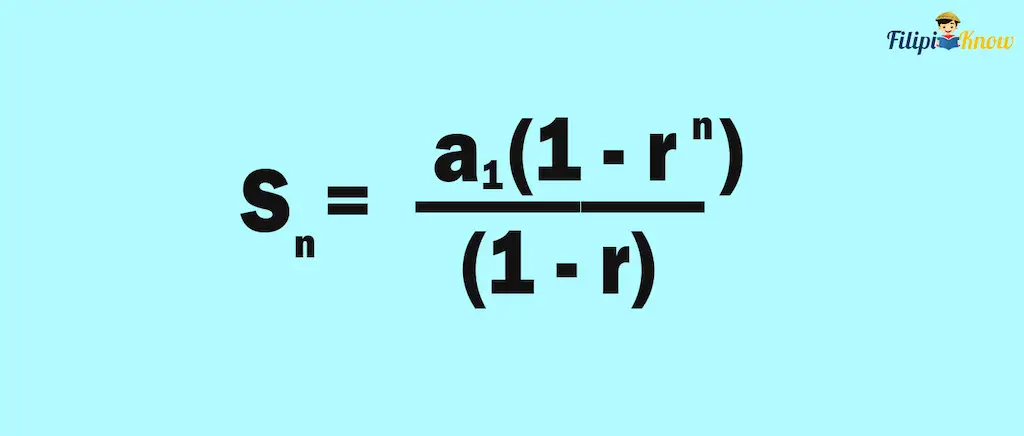
Such that:

• a₁ is the first term (or addend) of the geometric series
• r is the common ratio
• n is the number of terms being added

Sample Problem 1: Compute the sum of the first 15 terms of the geometric series 1 + 2 + 4 + 8 + …

Solution: 

• The first term of the sequence is 1. So we have a₁ = 1
• The common ratio is 2 (2 ÷ 1 = 2). So we have r = 2
• We are looking for the sum of the first 15 terms. Thus, we have n = 15.

Let us substitute these values for the formula for the sum of a finite geometric series.

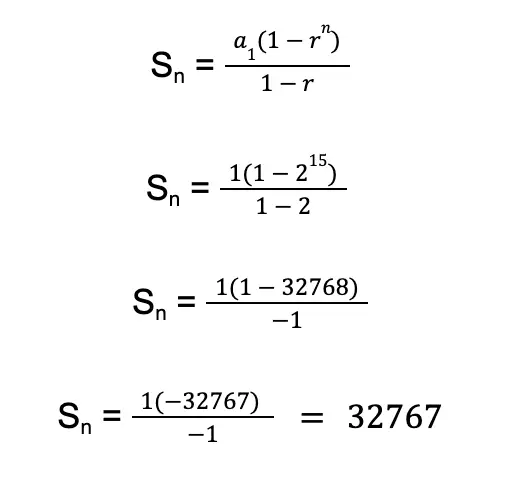
Based on our calculation above, the sum is 32,767. 

Sample Problem 2: Compute the sum of the first six terms of the sequence -3 + 12 + (-48) + …

Solution: 

• The first term of the sequence is -3. So we have a₁ = -3.
• The common ratio is -4 (12 (-3) = -4). So we have r = -4
• We are looking for the sum of the first 6 terms. Thus, we have n = 6.

Let us insert these values into the formula for a finite geometric series sum.

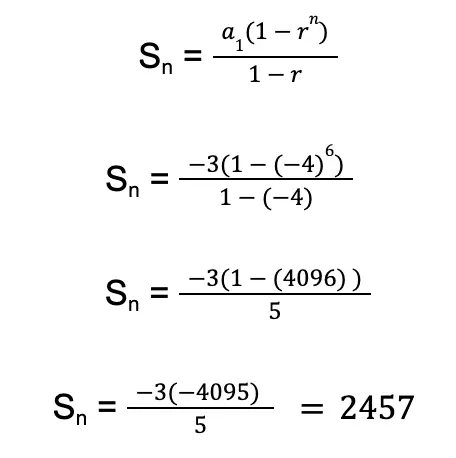
Based on our calculation above, the sum is 2,457.

Formula To Find the Sum of an Infinite Geometric Series

Shown below is the formula for the sum of an infinite geometric series.

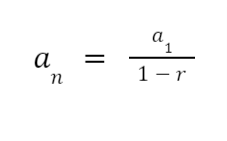
Such that:

• a₁ is the first term (or addend) of the geometric series
• r is the common ratio such that 0 < | r | < 1

Sample Problem: What is the value of ½ + ¼ + ⅛ + …?

Solution: The first term of the sequence is ½. So we have a₁ = ½.

Meanwhile, the common ratio is ½ (¼ ÷ ½ = ½)

By substitution:

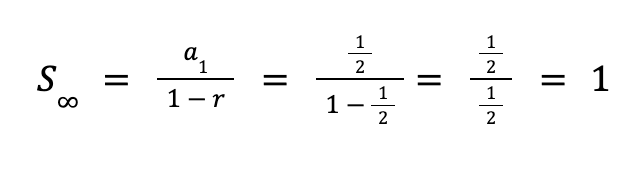
Thus, ½ + ¼ + ⅛ + … = 1

BONUS: A Geometric Interpretation on Infinite Geometric Series

We have learned earlier that using the formula for infinite geometric series, the sum of ½ + ¼ + ⅛ + 1/16 + .. is equal to 1. Although this formula is mathematically sound and valid, I know that this is still too abstract and difficult to grasp.

Using geometry, we can provide a more intuitive explanation of why ½ + ¼ + ⅛ + 1/16 + .. = 1.

Imagine we have a ½ sheet of colored paper placed on a table.

Now, let us place a ¼ sheet of colored paper near the ½ sheet of colored paper.

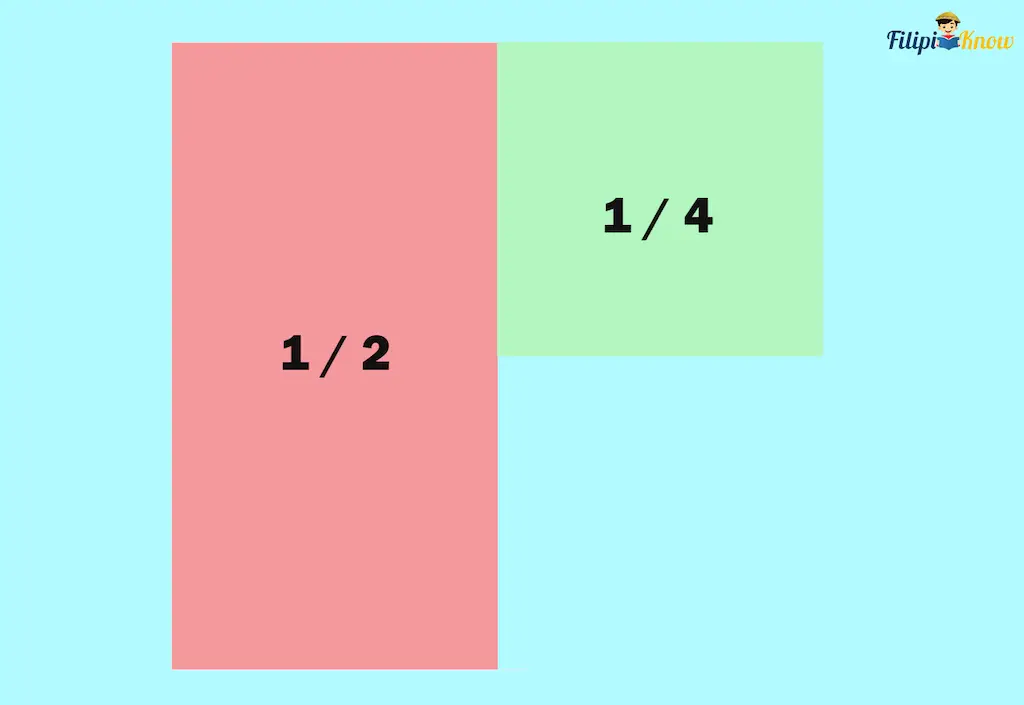
Add a ⅛ sheet of colored paper.

Add a 1/16 sheet of colored paper. We also perform this step for 1/32, 1/64, 1/128, etc. 

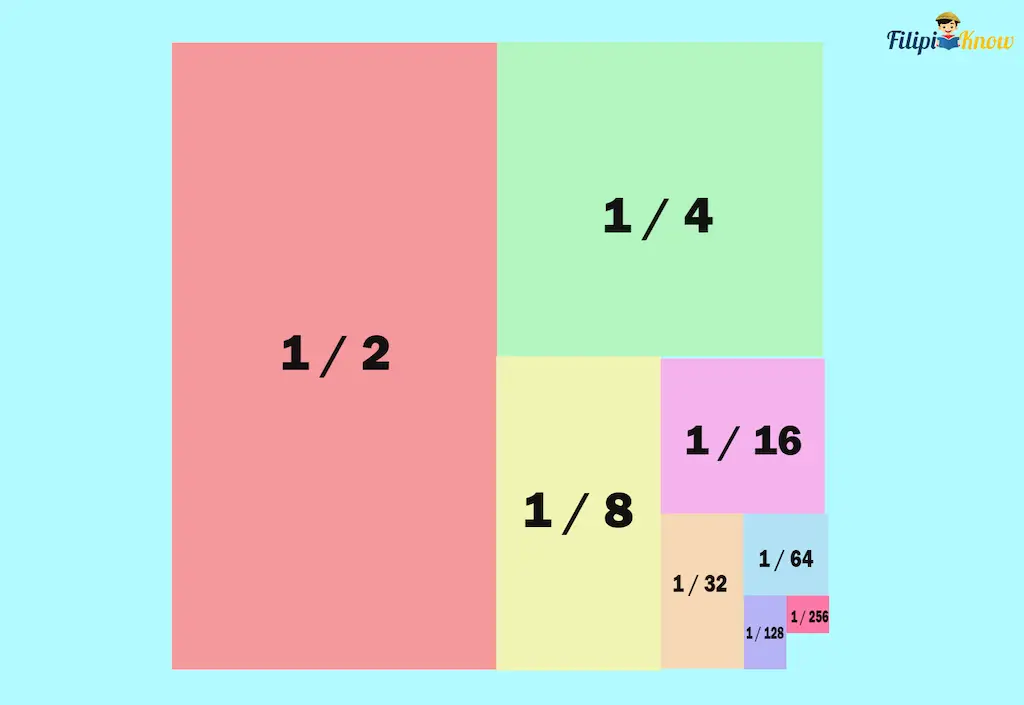
Doing this method multiple times allows us to obtain a total amount of paper equivalent to 1 whole sheet of colored paper. 

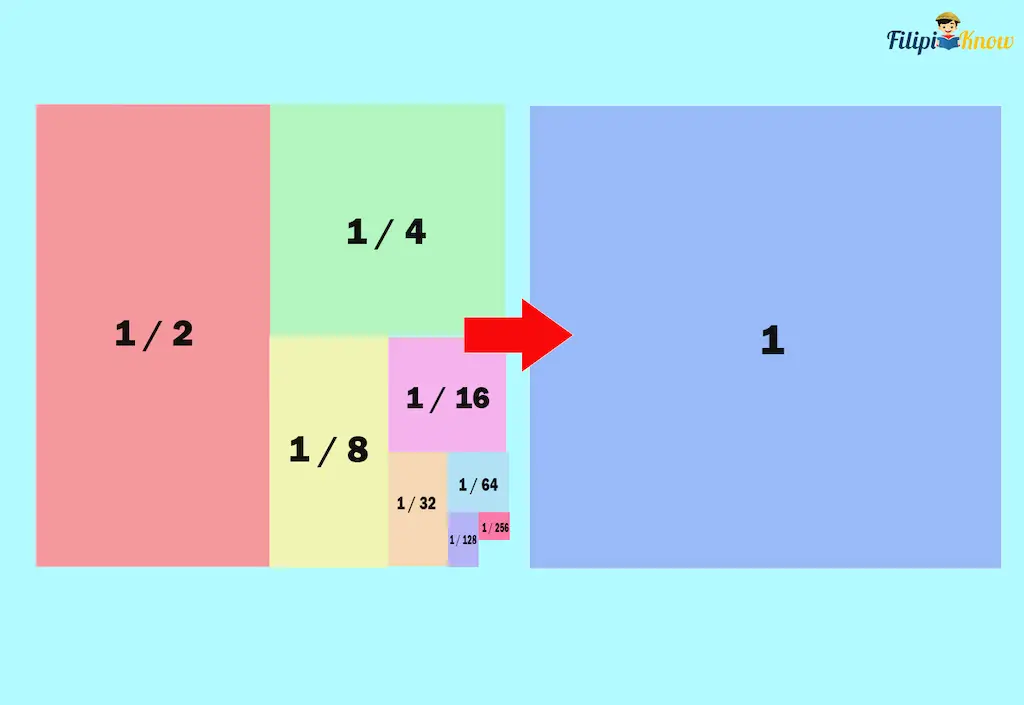
This shows that ½ + ¼ + ⅛ + 1/16 + .. = 1.

Next topic: Using Algebra to Solve Word Problems

Previous topic: Cartesian Coordinate System

Return to the main article: The Ultimate Basic Math Reviewer

Download Printable Summary/Review Notes

Download Printable Flashcards

Test Yourself!

1. Practice Questions [Free PDF Download]

2. Answer Key [Free PDF Download]

3. Math Mock Exam + Answer Key