Basic Geometry Concepts: Undefined Terms, Definitions, Postulates, and Theorems
The world consists of various objects in different forms and shapes. Humans have been fascinated with ways to measure these objects as early as the Egyptian and Greek civilizations. This fascination with measurement and shapes has led to the building of architectural marvels that prove human ingenuity throughout the ages–from the timeless pyramids to breathtaking skyscrapers.
Geometry is the branch of mathematics that deals with measurements, forms, and shapes. It comes from the Greek words geo, which means Earth, and metron, which means measure. The origin of the word itself already provides a clue to what geometry is all about and that is to measure everything we can see on this planet.
The geometry study starts with three undefined terms: point, line, and plane. Every other geometric concept is derived from these undefined terms. In this introduction to geometry, we will explore the undefined and defined terms in geometry and the concepts of postulates and theorems.
Click below to go to the main reviewers:
Ultimate PMA Entrance Exam Reviewer
Ultimate PNP Entrance Exam Reviewer
Table of Contents
4. Collinear and Coplanar Points
1. A straight line can be drawn by joining any two points
2. Any straight line segment can be extended infinitely in a straight line
3. A circle can be drawn with any center and any radius
4. All right angles are congruent
Convex and Non-convex Polygons
Types of Polygons According to the Number of Sides
Equilateral and Equiangular Polygons
Number of Diagonals of a Polygon
Download Printable Summary/Review Notes
1. Practice Questions [Free PDF Download]
2. Answer Key [Free PDF Download]
3. Math Mock Exam + Answer Key
Undefined Terms of Geometry
We use formal definitions in geometry to precisely refer to a particular concept.
For example, a triangle is a geometric concept defined as “a type of polygon with three sides and three vertices.” Using this formal definition, we know precisely what a triangle is; it tells us that a pizza is triangular, but a ball is not.

However, before we can provide a formal definition of geometric concepts, we must first recognize some concepts we cannot define precisely. These terms are known as undefined terms.
There are three undefined terms in geometry: point, line, and plane.
Why are these terms undefined?
The point, line, and plane cannot be defined easily because they are the building blocks of geometry. Exploring and combining these terms will provide us with other geometric concepts.
How can we define these terms if they are the “foundations” of our study?
Although we cannot formally define what a point, line, or plane is, we can develop an intuition on what these terms are. For instance, the tip of your ballpen is a representation of a point, the edge of your notebook is a line, and the surface of your table is a plane.
Let’s now provide descriptions of these undefined terms in geometry and look for their real-life representations.
1. Point
A point has no length or thickness. In other words, it has no dimension.
We use a dot to provide a visual representation of a point. Furthermore, we use capital letters to give a name to a certain point.
Some real-life representations of a point are the tip of a pencil or a certain coordinate in a map.

2. Line
A line is created by connecting at least two points. It has infinite length but no thickness. In other words, a line has only one dimension.
Shown below is a line connecting points A and B. We call this line AB. To name a line, we use any of the two points in the line. For instance, the line below, AB, can also be named line BC.
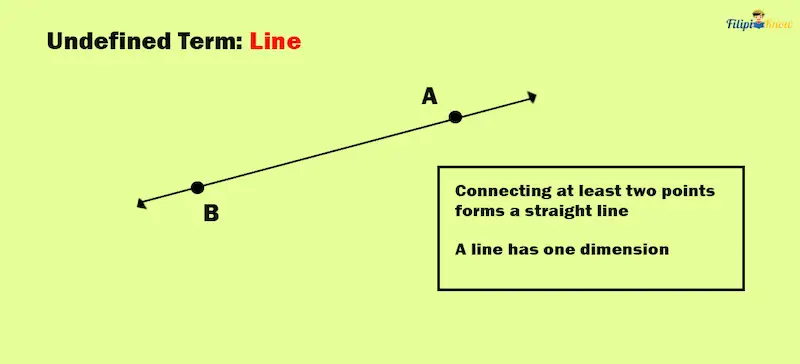
We can also put a two-way arrow sign (⟷) above AB to indicate that the AB geometric figure is a line.
The arrow signs you can see in a line tell us that it extends infinitely or without end.
Some real-life representations of a line are the edge of your ruler, book, or table.
3. Plane
A plane is a two-dimensional geometric figure. It has an infinite length and width. We usually use flat shapes such as squares, triangles, or parallelograms to represent a plane.

Using any three points that are not on the same line, we can create a plane. In the figure above, points A, B, and C form a plane.
Some real-life representations of a plane are the surface of your study table, a sheet of bond paper, or the floor of a house.
Example: Determine all the points, lines, and planes you can see below:
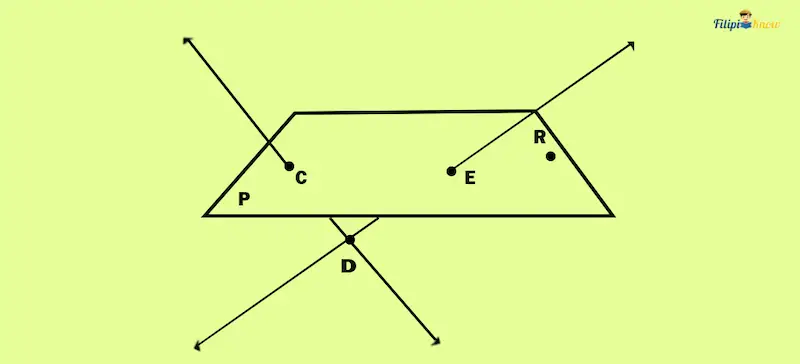
Solution:
- The points in the figure above are C, D, E, and R.
- The lines in the figure above are lines CD and DE.
- The plane in the figure above is plane P which contains points C, E, and R.
4. Collinear and Coplanar Points
If two or more points are located in the same line, then the points are collinear. On the other hand, if two or more points are located in the same plane, then the points are coplanar.
Example:
Please refer to the following illustration:
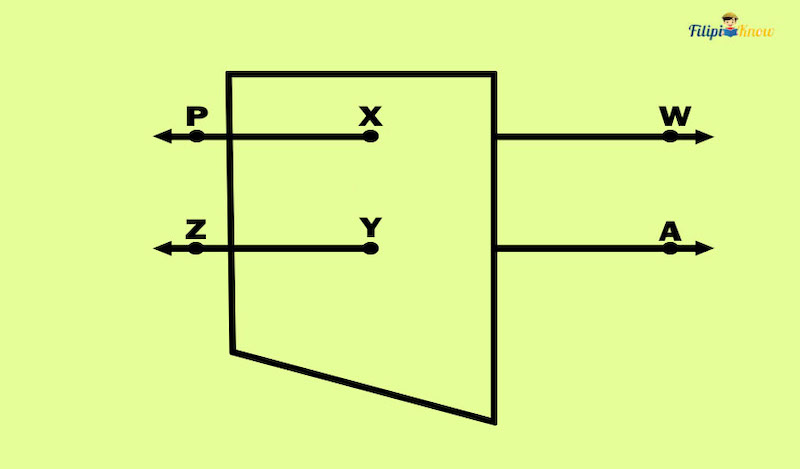
Using the given illustration above, determine:
- All points are collinear with point X.
- All points are coplanar with point Y.
Solution:
- Points P and W are collinear with point X since they are in the same line, particularly line PW.
- Point X is coplanar with point Y since they are in the same plane.
Using the undefined terms we have discussed here, we can now provide formal definitions for other essential geometric terminologies.
Definitions in Geometry
There are a lot of geometric concepts in geometry, and we must ensure that we are defining them precisely. If we fail to provide a precise definition of a particular concept, it can be hard to know what we are referring to.
For example, defining a square simply as “a polygon with four sides” lacks precision since rhombi (plural form of rhombus), rectangles, trapezoids, and parallelograms also have four sides.
We don’t want to give vague or ambiguous definitions of geometric concepts, hence the importance of knowing their exact or formal definitions.
In this section, we’ll provide precise definitions of different geometric terms you will encounter in your geometry study. Note how the undefined terms are used to define these “defined” terms.
1. Segment (or Line Segment)
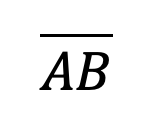
A line segment AB consists of the points A and B and all the points in line AB between A and B.
Look at line AB below:

Segment AB is the part of the line that is between A and B (points A and B are also included). All points in the line that is not in between A and B are not part of segment AB.
Points A and B in segment AB are called endpoints. Endpoints are the boundaries of a line segment.
This means that, unlike a line, a segment does not extend infinitely.
2. Ray
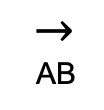
A ray AB consists of endpoint A and all points in line AB on the same side of A as B.
The formal definition of the ray written above seems too technical, but let us talk about it more descriptively.
A ray looks like a line with a fixed starting point but has no endpoint.
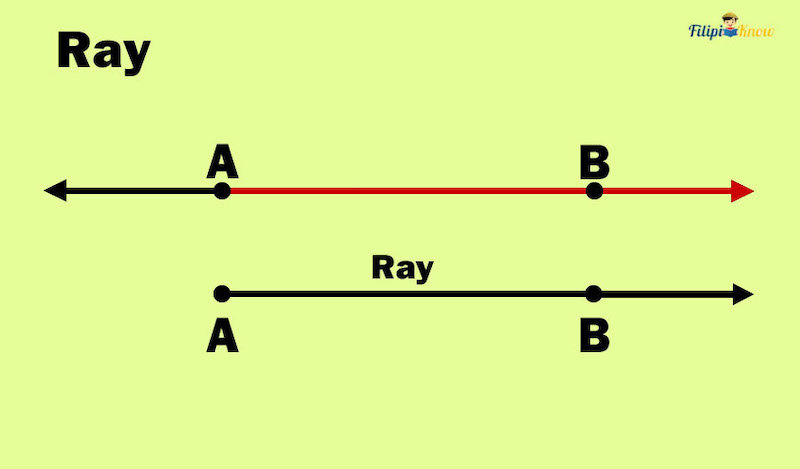
In the given illustration above, A is the starting point of the ray, but it extends infinitely beyond point B. Hence, we have the ray AB.
3. Intersection
Two or more geometric figures intersect if they have two or more common points.
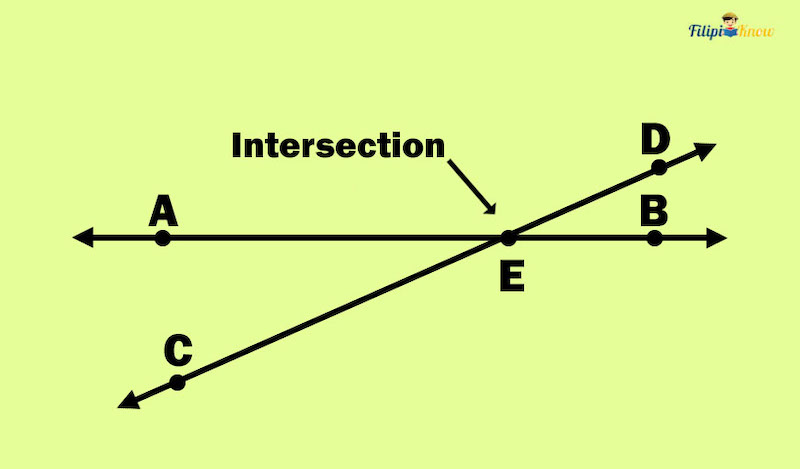
As you can see above, lines AB and CD intersect since they have a common point: point E.
An intersection is a point where two or more geometric figures meet.
If two or more lines intersect, then they intersect at a point. On the other hand, if two or more planes intersect, then their intersection is a line.
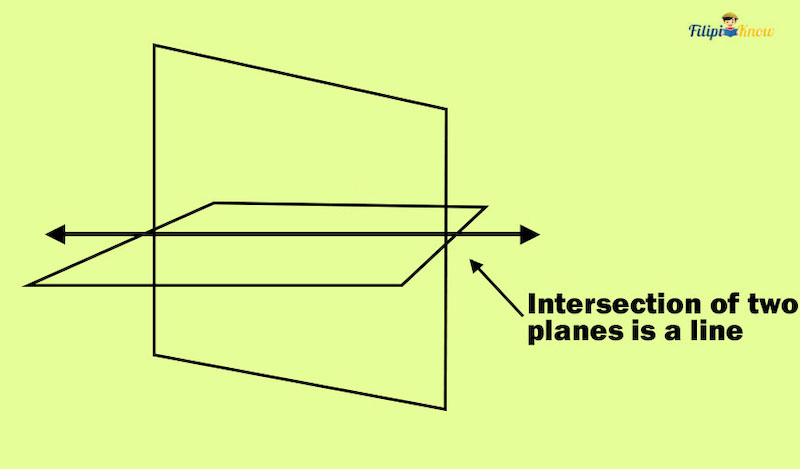
4. Parallel Lines
If two lines always have the same distance apart and will never intersect, the lines are called parallel lines.
As you can see below, lines l1 and l2 do not intersect. Even if you extend them infinitely, certainly, they will never intersect. Thus, we conclude that lines l1 and l2 are parallel lines.

5. Angles
An angle consists of two different rays that have the same endpoint.
If you have two rays with a common endpoint, you have formed an angle. Shown below is an example of an angle.
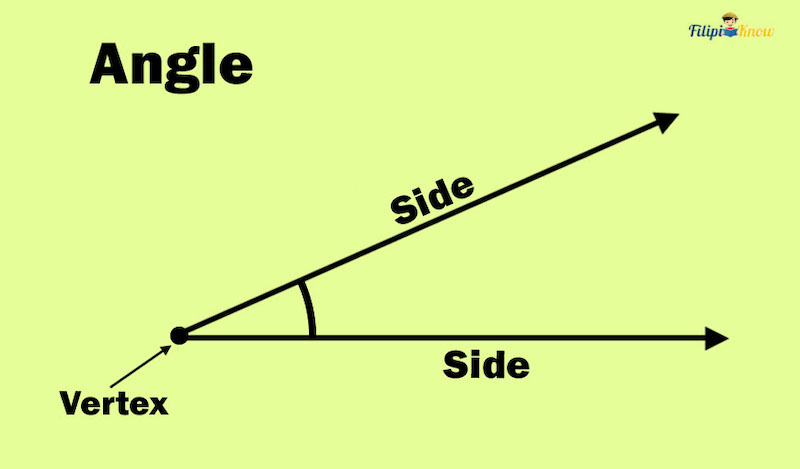
The common endpoint of the rays of an angle is called a vertex, while the rays are called the sides.
Note: The “endpoint,” as used in the context of angles, refers to a boundary that limits the rays from extending infinitely. Thus, the endpoint is not necessarily an “end” or a final destination of a ray but refers to a fixed point where a portion of the ray is not extending.
Angles have a lot of significant applications in geometry. For this reason, we will study them more rigorously in the next chapter.
At this point in our review, we have already defined some important geometric concepts. These terms will suffice for now as we explore the basic postulates of Euclidean geometry.
Euclidean Geometry
Geometry is a vast area of mathematical study. For this reason, we will narrow down the scope of this reviewer to one of the most essential geometric systems—Euclidean geometry.
Euclidean geometry has been attributed to Euclid, a Greek mathematician. Euclidean geometry focuses on geometric figures, shapes, and planes first discussed by Euclid in his famous book Elements.

In his book, Euclid introduced the five main postulates of geometry. Postulates are statements that we have accepted as true even without proof. These statements are the basic rules or principles in the study of geometry. We assume that these statements are true since they are intuitive and allow us to create more concepts that were derived from them.
Euclid’s Five Postulates
Euclid used the undefined and some defined terms in geometry to devise the following postulates:
1. A straight line can be drawn by joining any two points
We have previously mentioned that a line can be created by connecting at least two points.
2. Any straight line segment can be extended infinitely in a straight line
This means you can extend both sides to form a straight line if you have a line segment.
3. A circle can be drawn with any center and any radius
According to Euclid, if we draw a point and assume it is the center of the circle, we can draw a radius or a line segment with the center as one of its endpoints and create a circle out of it (more about circles in the succeeding chapters/modules).

4. All right angles are congruent
Right angles are angles measuring exactly 90°. Since all right angles measure 90 degrees, it is logical to say that all right angles are congruent or have the exact measurement (more about the measurement of angles in the next reviewer).
5. For every line and a point that does not belong to that line, there is only one line that passes through that point parallel to the given line
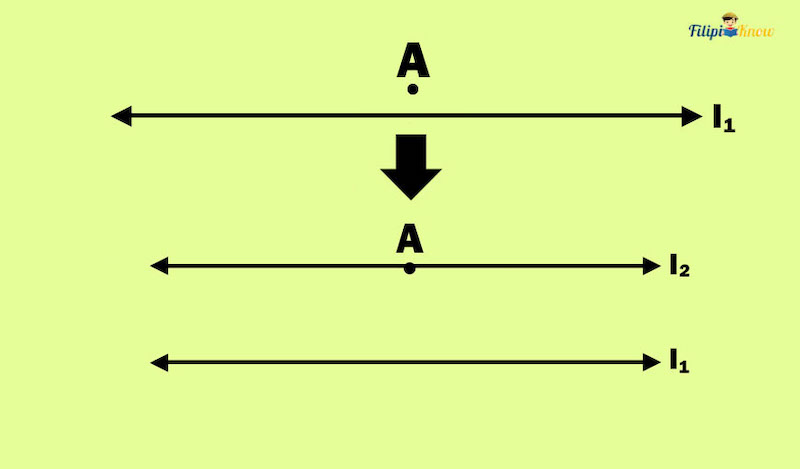
Euclid’s fifth postulate, more commonly known as the “parallel postulate,” states that given any line and a point that is not in that given line, you can only construct one line that passes through that point and that will never intersect with the given line even if you extend it infinitely.
In the image above, we have line l1 and point A, which is not in line l1. According to the postulate, we can draw only one line that passes through point A and is parallel to l1 (that line is l2).
The fifth postulate is one of the most popular postulates in geometry since many mathematicians have attempted to prove it using the first four postulates of Euclid. However, until recently, no one succeeded in proving it.
Furthermore, some mathematicians tried to drop the fifth postulate and create a new system of geometry known as non-Euclidean geometry (which is beyond the scope of this reviewer).
The postulates above are the foundations of the geometry we are studying nowadays. Again, remember that postulates are statements we agree with and assume as true without formal proof.
There are a lot of postulates in geometry, and we cannot cover them all in a single reviewer. For this reason, we will discuss only those important postulates for those who are just beginning to study geometry.
Ruler Postulate
The points in a line can be matched to the elements of the set of real numbers.
The ruler postulate allows us to match real numbers to the points in the line.

In the given line above, we assign point A to the real number 5 and point B to the real number 12.
Once we have assigned real numbers to specific points in a line, we can determine the distance between A and B.
The distance between A and B is given by |A – B| or the absolute value of the difference between the real numbers assigned to A and B.
Thus, in the given line above, the distance between A and B is |5 – 12| = |-7| = 7 units
The distance between points A and B can also be considered as the measure of the line segment AB. Since we have determined that the distance between A and B is seven units, the line segment AB is likewise seven units long.
Segment Addition Postulate
If points A, B, and C are collinear and point B is between A and C, then AB + BC = AC.

This postulate is very intuitive. If we want to determine the distance between A and C, we can add the distance between A and B and between B and C.
Example 1: How long is XZ if XY = 32 and YZ = 10?
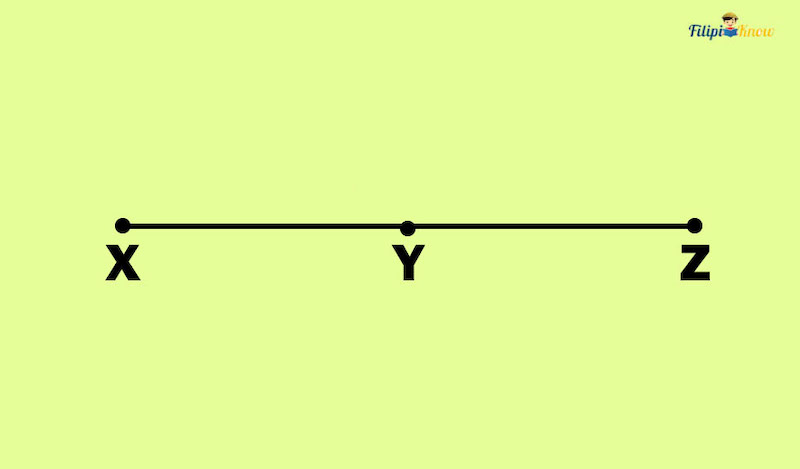
Solution:
Using the segment addition postulate:
XY + YZ = XZ
32 + 10 = 42 units
Example 2: Using the same figure in the previous example, determine the value of a if XZ = 12, XY = 2a, and YZ = 10 – a.
Solution:
The segment addition postulate tells us that XY + YZ = XZ. Given the respective values of each segment, we can set up the equation as follows:
XY + YZ = XZ
2a + (10 – a) = 12 Substituting the given values
We can simplify the given equation above as follows:
a + 10 = 12
a = 12 – 10 Transposition method
a = 2
Thus, the value of a is 2.
Given the value of a we have obtained above, we can substitute it for the original values of XY and YZ. The length of XY is 2(2) = 4 units and the length of YZ = 10 – (2) = 8 units. You can verify that by adding the lengths of XY and YZ, which will give you the sum of 12. This is equivalent to the length of XZ, which is also 12 units.
Midpoint of a Segment
The midpoint of a segment is the point that divides the segment into two equal parts.
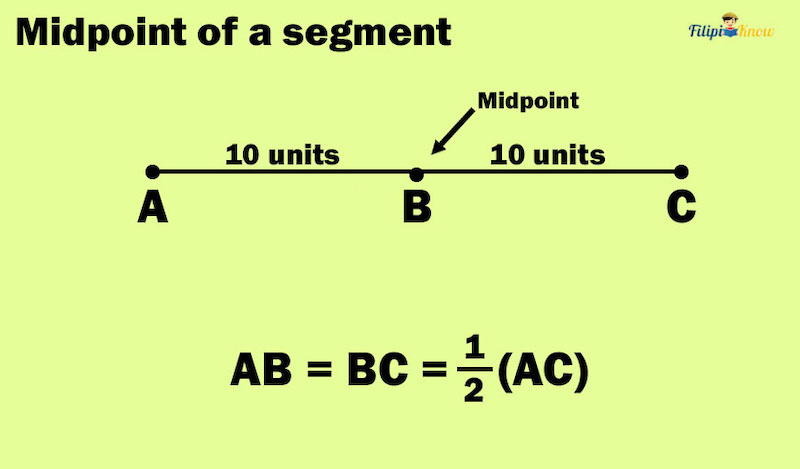
In the figure above, segments AB and BC are 10 units long. Thus, B is the midpoint of segment AC.
Since the segment addition postulate tells us that if B is between AB and BC, then AB + BC = AC. We can conclude that when B is the midpoint of AC, AB or BC can be derived if we divide AC by 2.
Example: Suppose that points P, Q, and R are collinear points such that Q is between P and R and PQ = QR. Determine the length of PR if QR = 12.
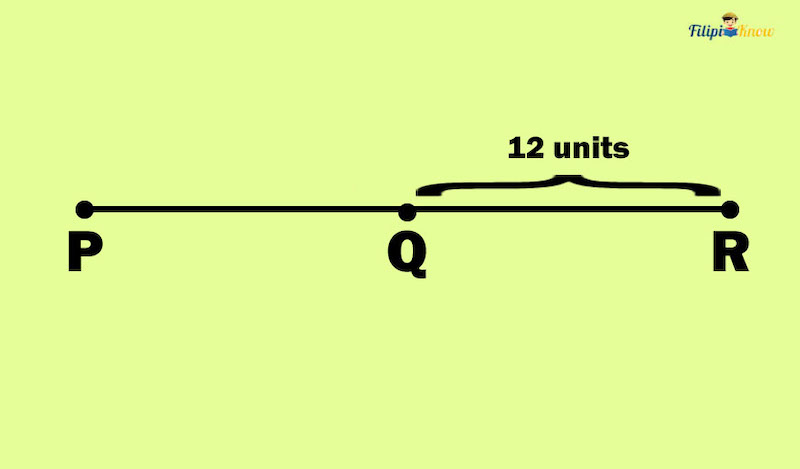
Solution:
Method 1
Since Q is between P and R and PQ = QR, we can conclude that Q is the midpoint of PR.
To obtain PR, we can double the QR value since PQ = QR.
PR = QR x 2
PR = 12 x 2
PR = 24
Thus, PR is 24 units long.
Method 2
Since Q is between P and R and PQ = QR, we can conclude that Q is the midpoint of PR.
Furthermore, since Q can be located between the points P and R, we can apply the segment addition postulate:
PQ + QR = PR
Using the given value of QR (which is 12):
PQ + 12 = PR
Since PQ = QR:
12 + 12 = PR
24 = PR
PR = 24
Hence, PR is 24 units long.
Bisecting a Line Segment
When we “bisect” a line segment, it simply means dividing a line into two equal parts using a line. The line that bisects a line segment is called the “bisector.”
The intersection of the bisector and the line segment is the midpoint of the line segment.
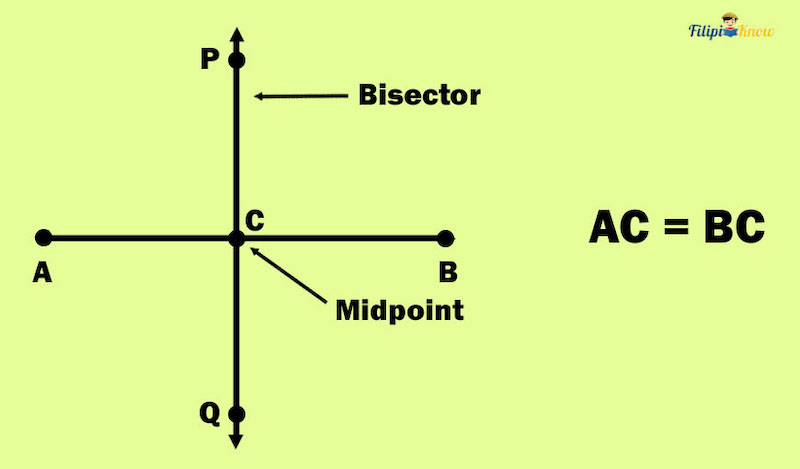
In the figure above, line PQ bisects segment AB. AB is divided or bisected into segments AC and CB. Note that segments AC and CB are equal in length, and C is the midpoint of AB.
In the succeeding reviewers, you will learn that we can also bisect angles and plane figures.
Theorems
Theorems are statements that are deduced or logically obtained from definitions and postulates. Unlike postulates, the truthfulness of a theorem can be proven mathematically using the postulates we have laid out.
There are a lot of theorems in geometry that various mathematicians and geometers have proved. One of the most famous theorems in geometry is the Pythagorean theorem, attributed to Pythagoras, a Greek philosopher who has provided proof for this theorem.
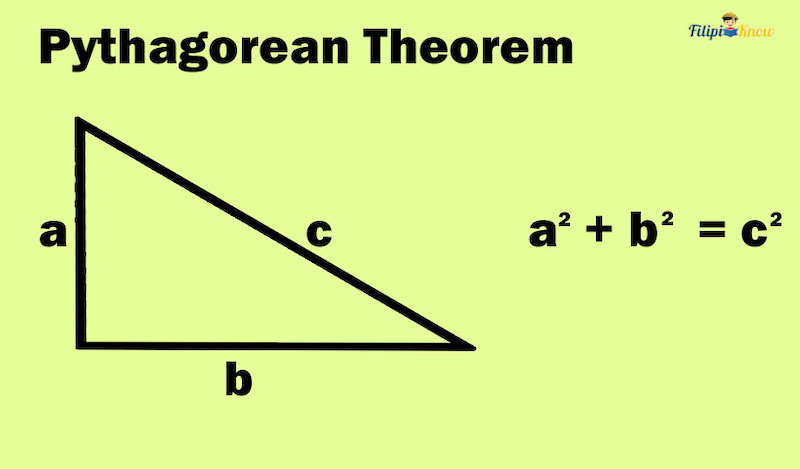
The Pythagorean theorem was also proven by Chinese mathematician Liu Hiu, US President James Garfield, and much more. All in all, there is a total of 300 proofs for this theorem.
The Pythagorean theorem states that in a right triangle, the sum of the squares of the lengths of the two shorter sides is equal to the square of the length of its longest side.
Congruence
In geometry, we are always interested in figures that have equal or the same values as they provide us with significant insights. If two geometric figures have the same shape and size, they are congruent.
Congruent Segments
Two segments are congruent if they have the same lengths.
Suppose line segments CD and EF have the same length and are both equivalent to 32 (i.e., CD = 32 and EF = 32). Thus, CD and EF are congruent segments. We use the symbol ≅ to show congruence, but we will use the equal sign “=” to show that the segments have equal measurements.
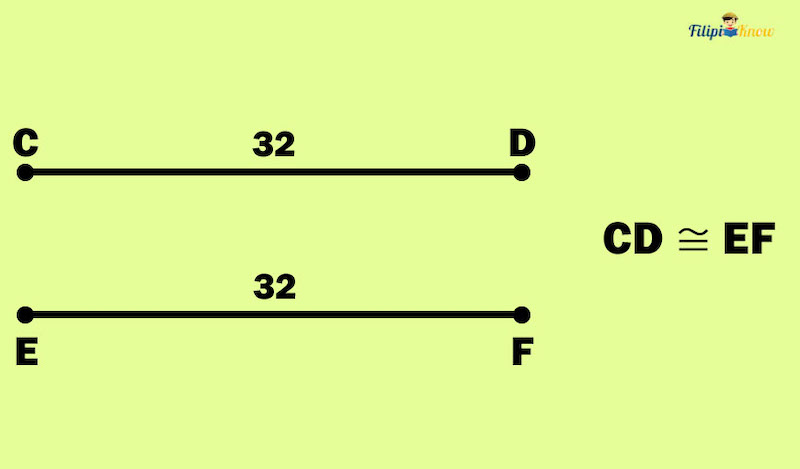
Note also that the midpoint or a bisector divides a line segment into two congruent segments.
Example: Line XY bisects segment OP at point S. If OP = 3x – 2 and PS = x, what is the value of x?
Solution:
It will be easier if we illustrate the given problem above.
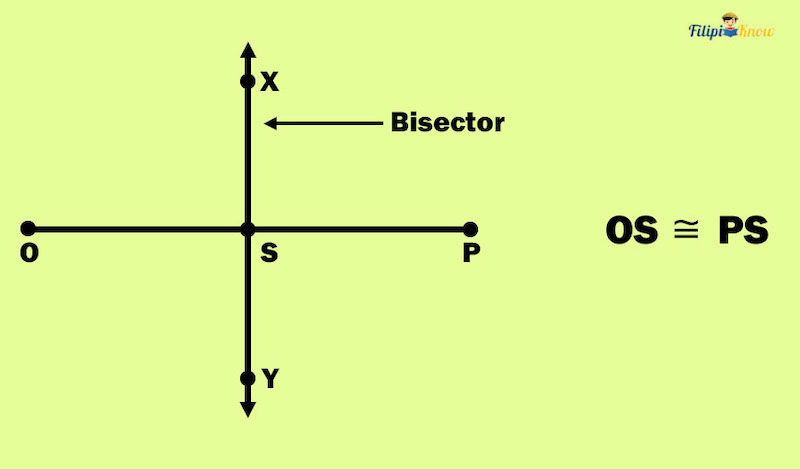
Since line XY bisects OP at point S, then S is the midpoint of OP. It means that S divides OP into congruent segments OS and PS.
Since PS = x, then OS is also equal to x.
Using the segment addition postulate:
OP = PS + OS
3x – 2 = x + x Using the given lengths of OP and PS
3x – 2 = 2x
3x – 2x = 2 Transposition method
x = 2
Thus, the value of x must be 2.
Congruent Angles
Like congruent segments, congruent angles have the same measure (we use degrees to measure an angle).
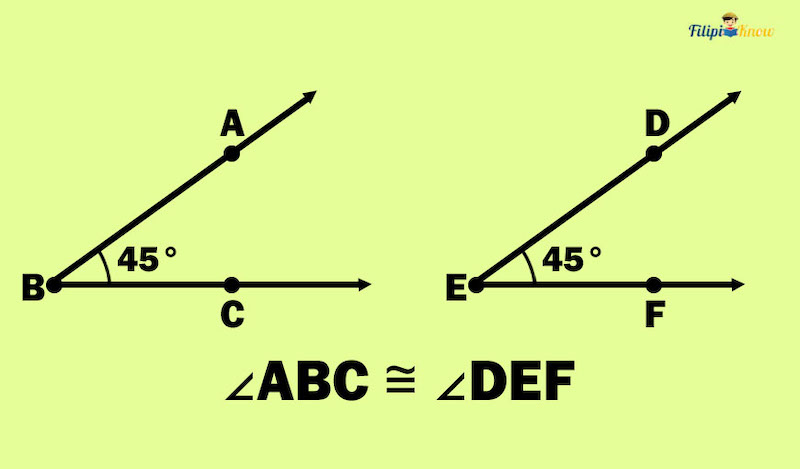
You’ll learn more about angles and congruent angles in the next chapter.
Polygons
We have already discussed some geometric figures in one dimension (i.e., lines, line segments, and rays). In this section, we’re now covering two-dimensional figures, also known as planes.
A plane figure is a geometric figure that is on a plane. If a particular shape or object lies on a plane, it is considered a plane figure.
A polygon is a closed-plane figure formed by three or more line segments.
Take note of the word “closed”; this means that all endpoints of the line segments must touch an endpoint of another segment. The points where these line segments touch the endpoint of another line segment are called the vertices or the corners of the polygon.
Examples of polygons are the elementary shapes we are all familiar with: squares, rectangles, triangles, etc. However, polygons are a broad set of plane figures which we will discuss thoroughly in this section.
Convex and Non-convex Polygons
A convex polygon is a polygon whose interior angles measure less than 180°. The interior angles refer to the angles located inside a polygon (we will learn more about them in the succeeding module). On the other hand, if at least one of the interior angles of a polygon measures more than 180°, then that polygon is a concave polygon.
It’s easy to identify whether a polygon is convex or concave if the measurements of its interior angles are given. However, these values are usually not presented in a given polygon, or a protractor is unavailable. Hence, we need a method that can help us to identify whether a polygon is convex or concave without referring to the measurement of the interior angles.
One property of a convex polygon is that if you extend each of its sides, the line created from these sides will never cross the polygon’s interior. Take, for instance, the parallelogram below. Notice that as we extend each of its sides, none of these lines cross the interior of the parallelogram. Therefore, the parallelogram is a convex polygon.

To determine if a polygon is convex or not, do the following:
- Extend each side of the given polygon infinitely, just like a line.
- If one of those extended sides crosses the interior of the given polygon, then the polygon is non-convex. Otherwise, the polygon is convex.
The polygon below is non-convex since there’s a side that crosses the interior of the given polygon when extended as a line. In the figure, point X represents the part of the side that pierces through the polygon’s interior.
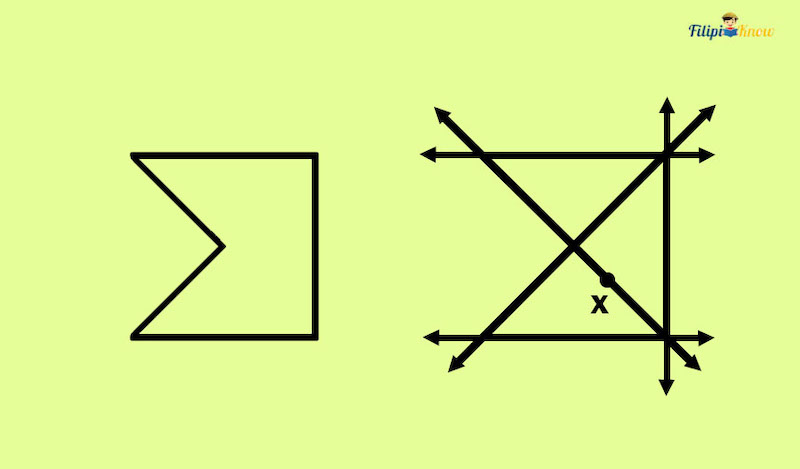
Example: Which of the following polygons is non-convex?
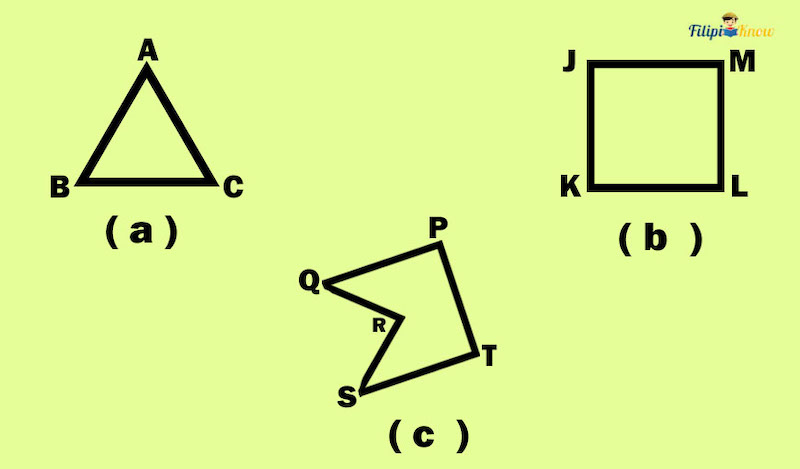
Solution:
Only the polygon in (c) is non-convex. Try extending each side of this polygon, and you will notice that two points branching off of QR and SR will appear as the lines extending from these two sides pierce through the polygon’s interior.
Types of Polygons According to the Number of Sides
We can classify polygons according to the number of sides they have, as shown in the table below:
| Number of sides | Name of the Polygon |
| 3 | Triangle |
| 4 | Quadrilateral |
| 5 | Pentagon |
| 6 | Hexagon |
| 7 | Heptagon |
| 8 | Octagon |
| 9 | Nonagon |
| 10 | Decagon |
| n | n-gon |
As you can see, a three-sided polygon is a triangle. Meanwhile, a four-sided polygon is called a quadrilateral. Quadrilaterals include squares, rectangles, rhombuses, trapezoids, and parallelograms. We can extend the classification of polygons into “n-gons” or polygons with n sides (where n is a whole number greater than or equal to 3).
Equilateral and Equiangular Polygons
An equilateral polygon is a polygon wherein all sides are congruent. Some examples of equilateral polygons are squares, rhombuses, and equilateral triangles.
On the other hand, an equiangular polygon has all of its interior angles congruent. Examples of equiangular polygons are rectangles.
If a polygon is both equilateral and equiangular, we call that polygon a regular polygon.
Diagonals of a Polygon
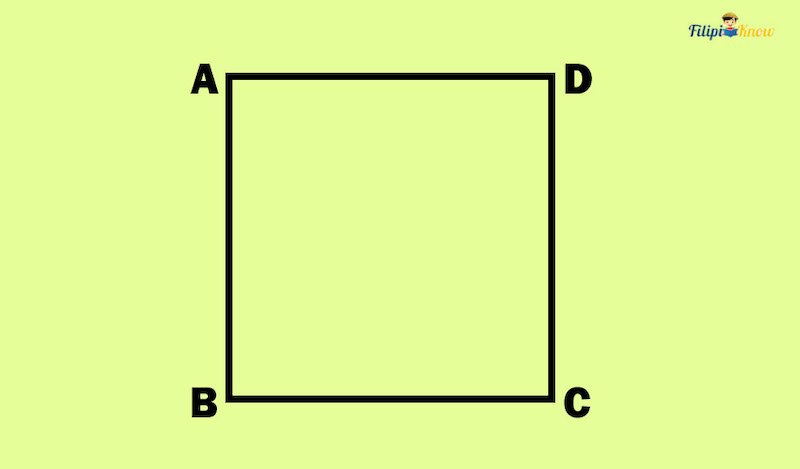
A diagonal is a line segment that connects a polygon’s corners (or vertices) that are not adjacent or next to each other.
Take, for instance, the square below. Points A and C are not adjacent corners. If you draw a line segment that connects A and C, you form the diagonal AC.
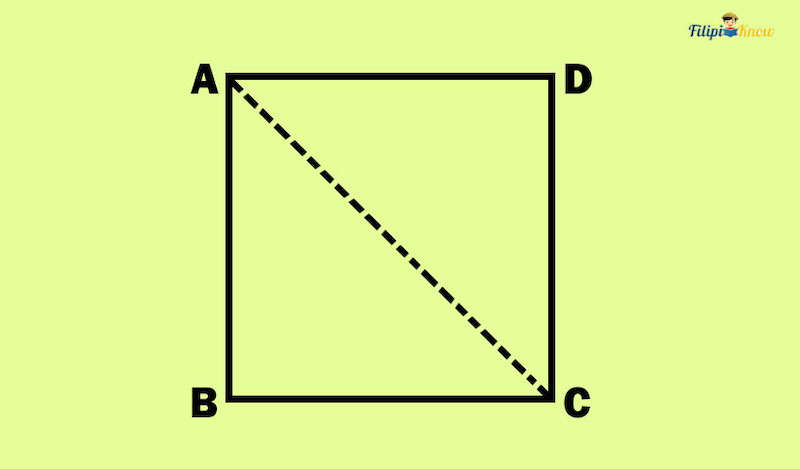
You can also create a diagonal by connecting the corners B and D. Why not try it yourself?
Number of Diagonals of a Polygon
You might have noticed that the square above has two diagonals. All four-sided polygons or quadrilaterals (rectangles, rhombuses, parallelograms) have two diagonals. Meanwhile, a triangle has no diagonal.
If a polygon has n sides, then the number of its diagonals can be determined using the formula below:

where n is the number of sides of the polygon.
Example: How many diagonals can you draw in a pentagon?
Recall that a pentagon has five (5) sides, so we have n = 5.
Let us determine the number of diagonals a pentagon has using the formula above.
Substituting n = 5 in the formula:

Thus, you can draw five diagonals in a pentagon.
Next topic: Angles
Previous topic: Using Algebra to Solve Word Problems
Return to the main article: The Ultimate Basic Math Reviewer
Download Printable Summary/Review Notes
Download Printable Flashcards
Test Yourself!
1. Practice Questions [Free PDF Download]
2. Answer Key [Free PDF Download]
3. Math Mock Exam + Answer Key
Copyright Notice
All materials contained on this site are protected by the Republic of the Philippines copyright law and may not be reproduced, distributed, transmitted, displayed, published, or broadcast without the prior written permission of filipiknow.net or in the case of third party materials, the owner of that content. You may not alter or remove any trademark, copyright, or other notice from copies of the content. Be warned that we have already reported and helped terminate several websites and YouTube channels for blatantly stealing our content. If you wish to use filipiknow.net content for commercial purposes, such as for content syndication, etc., please contact us at legal(at)filipiknow(dot)net
