Trigonometric Functions Examples With Solution

Trigonometry originated from the Greek words “trigonon,” which means triangle, and “metron,” which means measure.
From the origin of the word itself, it gives you an idea of what trigonometry is all about. Trigonometry is the branch of mathematics that deals with the relationship between the angles and sides of a triangle (especially right triangles). This study emerged from geometry in the 16th century and has proven to be a valuable and practical field of study.
The applications of trigonometry are immense. For instance, it was used to develop artillery science, aviation, navigation, engineering, the manufacturing industry, and even to model sound waves in music theory.
In this review, you’ll learn the first yet most crucial step in studying trigonometry: understanding the concept of the six trigonometric functions, also known as circular functions.
Click below to go to the main reviewers:
Ultimate PMA Entrance Exam Reviewer
Table of Contents
A Quick Review on Right Triangles
Before we proceed to the study of six trigonometric functions, let us first recall some important concepts involving right triangles. You must understand these concepts first because they will be the backbone of our trigonometric study.
A right triangle is a triangle that contains one interior right angle (90° angle) and two remaining interior angles which are acute.
The longest side of this triangle is called the hypotenuse, while the shorter sides are called the legs. Take note that the hypotenuse of a right triangle is always opposite the right angle.
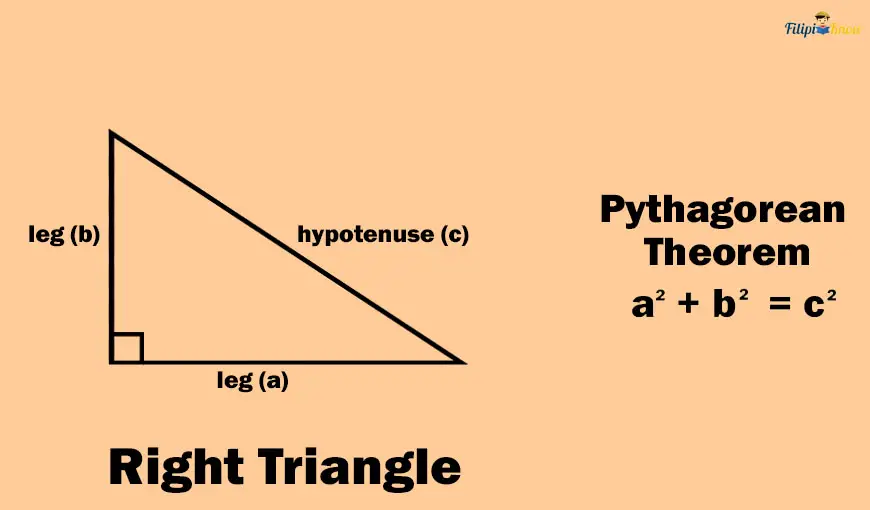
According to the Pythagorean theorem, the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse. In the symbol, a2 + b2 = c2, the a and b are the lengths of the legs of the right triangle, and c is the hypotenuse.
The trigonometry study focuses on the relationship of the sides of the right triangle to its interior angles. This relationship is exhibited using the six trigonometric functions or ratios discussed in the next section.
The Opposite and the Adjacent Sides of an Acute Angle of a Right Triangle
A right triangle has two acute angles. Note that these acute angles are complementary, or the sum of their degree measurements is 90°.
Take a look at the right triangle ABC below. Say we select one of the acute angles of this right triangle and name it angle θ (Greek letter “theta”).
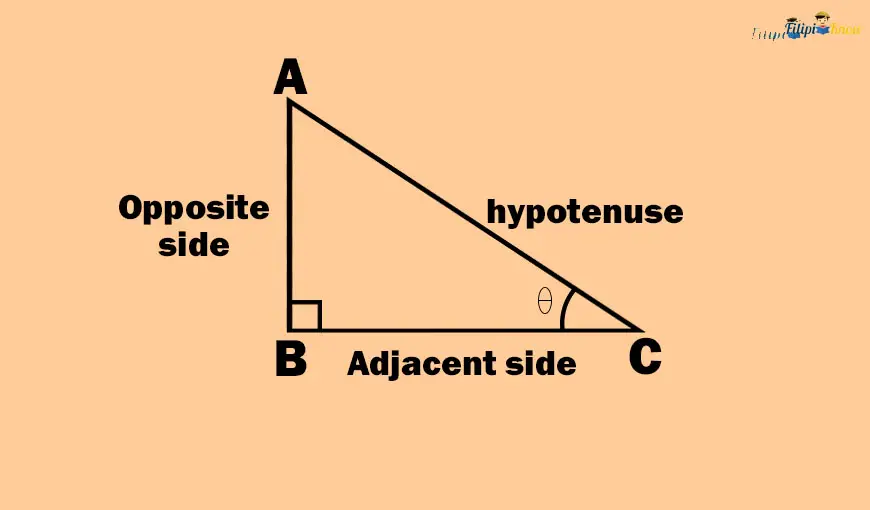
In a right triangle, an acute angle has a corresponding opposite side and an adjacent side.
The side of the right triangle that is opposite angle θ is called the opposite side. Thus, in the right triangle above, side AB is the opposite side of angle θ.
Meanwhile, the side of the right triangle close to angle θ is called the adjacent side. In the right triangle above, side BC is the adjacent side of the angle θ.
Please note that the opposite and adjacent sides of a right triangle are not fixed; they depend on where the acute angle is located. In our example above, we use angle θ as a reference; therefore, we have side AB as the opposite side and side BC as the adjacent side. However, if we select the other acute angle as a reference, our opposite and adjacent sides will change accordingly.
Let us use the other acute angle of the right triangle above. Let us call it angle x.
If we use angle x as our reference, the opposite side will be side BC while the adjacent side will be AB. In other words, our opposite and adjacent sides change as we select the angle x.
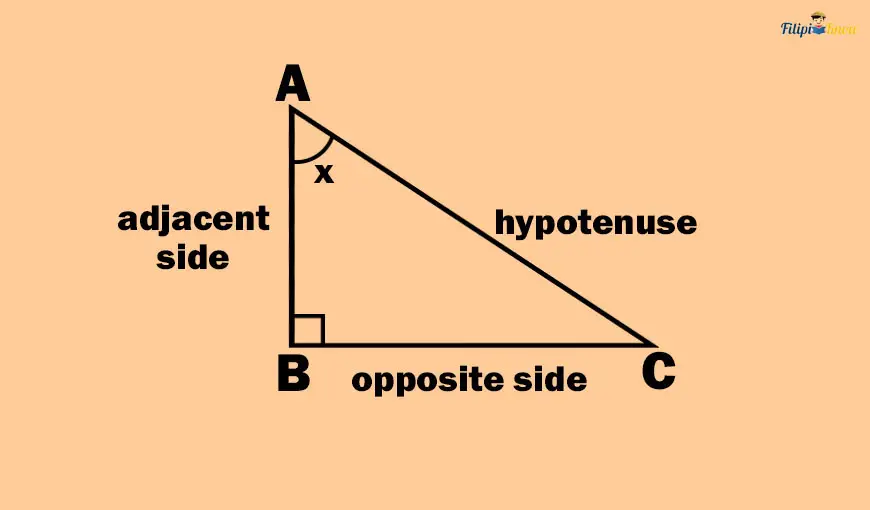
Take note that since the opposite and adjacent sides of an acute angle are still the legs of the right triangle, then by the Pythagorean theorem:
(Opposite Side)2 + (Adjacent Side)2 = (Hypotenuse)2
This means that the sum of the squares of the lengths of the opposite and adjacent sides of an acute angle of a right triangle is equal to the square of the length of its hypotenuse.
You must practice identifying the corresponding opposite side and the adjacent side of an acute angle of a right triangle because it is an essential skill in deriving the value of trigonometric functions.
Sample Problem:
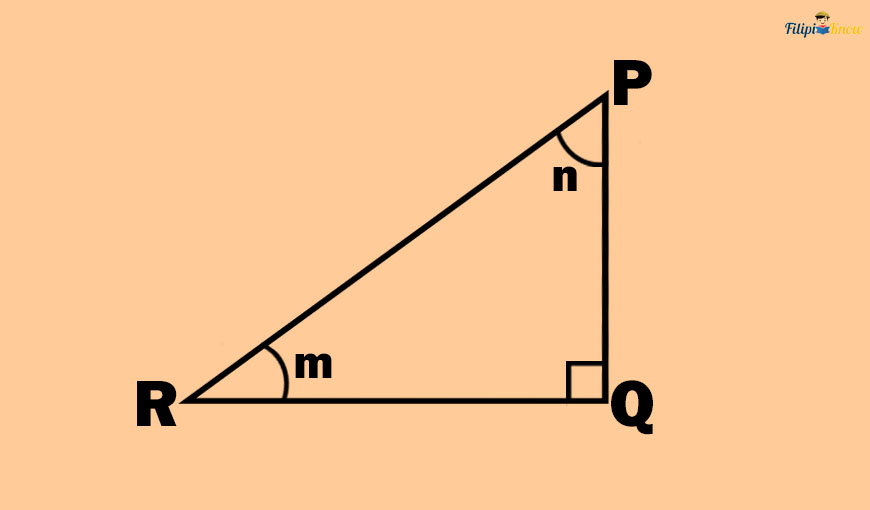
Using the right triangle above, determine the following:
- the opposite side of angle n
- the adjacent side of angle m
- the opposite side of angle m
Solution:
a. If we use angle n as the reference, the side opposite to it is side QR. Thus, the opposite side of angle n is side QR.
b. If we use angle m as the reference, the side adjacent to it is side QR. Thus, the adjacent side of angle m is side QR.
c. If we use angle m as the reference, the side opposite to it is side PQ. Thus, the opposite side of angle m is side PQ.
Now that you know how to determine the opposite and adjacent sides of an acute angle of a right triangle, we can discuss the six trigonometric functions.
Six Trigonometric Functions

The trigonometric functions or ratios are the ratios between the sides of a right triangle concerning an acute angle. Six trigonometric functions exist: sine, cosine, tangent, cosecant, secant, and cotangent. In this section, you’ll learn more about these functions and how to compute them.
To start our discussion, I want you to look at the right triangle below. We name one of the acute angles of this right triangle θ. Let’s define the six trigonometric functions using this angle θ.
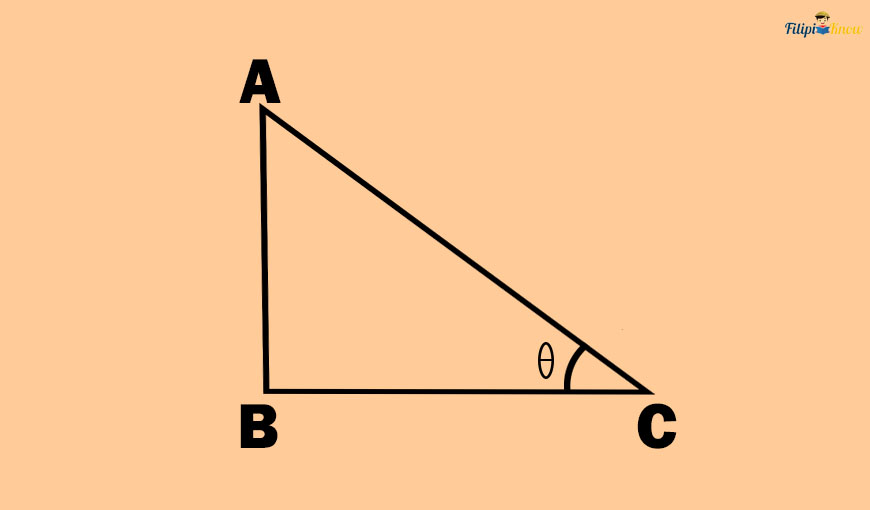
1. Sine
The sine (abbreviated as “sin” and read as “sayn”) of the acute angle θ is the ratio between the lengths of the opposite side of θ and its hypotenuse.
sine θ = opposite side/hypotenuse
This means that to find the value of the sine of angle θ, we must first determine the length of the opposite side of θ and then divide it by the length of the right triangle’s hypotenuse.
Say we put some measurements in the right triangle above.
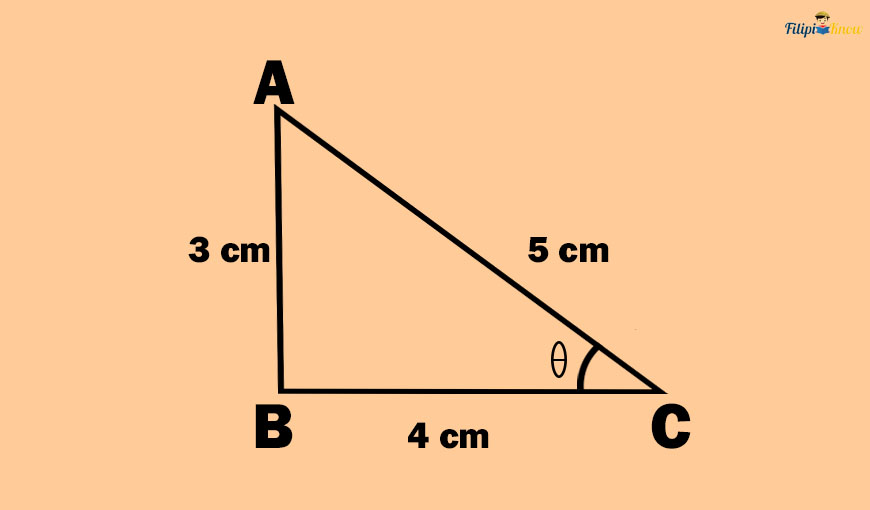
The opposite side of angle θ in the right triangle above is AB, which measures 3 cm. Meanwhile, the hypotenuse of this right triangle is 5 cm. Therefore, the value of the sine of θ or “sin θ” is:
Sine θ = opposite side/hypotenuse
Sine θ = ⅗
Thus, the sine of angle θ in the right triangle above is ⅗.
2. Cosine
The cosine (abbreviated as “cos” and read as “co-sayn”) of the acute angle θ is the ratio between the adjacent side of angle θ and the hypotenuse of the right triangle.
cosine θ = adjacent side/hypotenuse
This means that to find the value of the cosine of the angle θ, we must first determine the adjacent side of θ and then divide its length by the length of the right triangle’s hypotenuse.
Using the same right triangle, let us determine the cosine of θ.
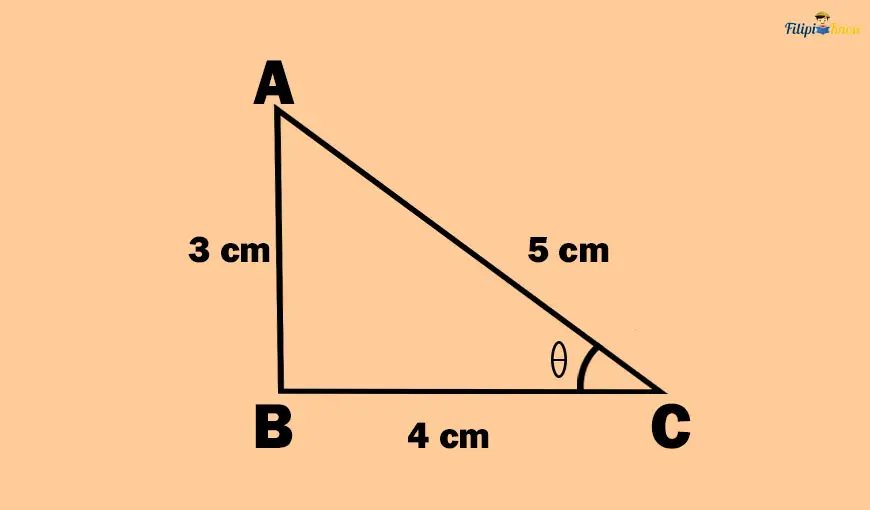
The adjacent side of angle θ in the right triangle above is side BC which measures 4 cm. Meanwhile, the hypotenuse of this right triangle is 5 cm. Therefore, the value of the cosine of θ or “cos θ” is
Cos θ = adjacent side/hypotenuse
Cos θ = ⅘
Thus, the cosine of angle θ in the right triangle above is ⅘.
3. Tangent
The tangent (abbreviated as “tan”) of the acute angle θ is the ratio between the opposite side and the adjacent side of the acute triangle of the right triangle.
tangent θ = opposite side/adjacent side
This means that to find the value of the tangent of the acute θ of a right triangle, we need to determine first the opposite and the adjacent sides of the right triangle. Afterward, we divide the length of the opposite side by the length of the adjacent side.
Using the same figure above, let us determine the tangent of θ:
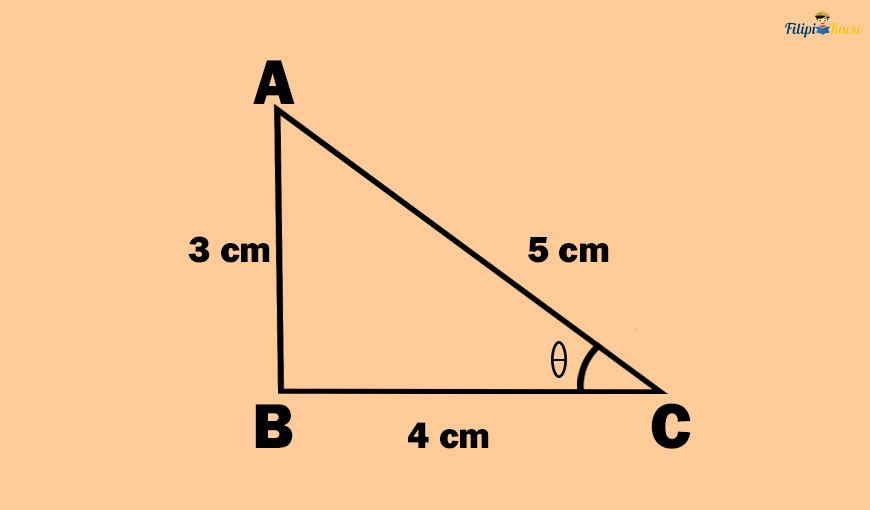
The opposite side of angle θ is side AB which measures 3 cm. Meanwhile, the adjacent side of angle θ is the side BC which measures 4 cm. So, the value of the tangent of θ or “tan θ” is
tangent θ = opposite side/adjacent side
tangent θ = ¾
Thus, the value of the tangent of θ in the right triangle above is ¾.
Before we proceed with the remaining three trigonometric functions, let us solve some examples first.
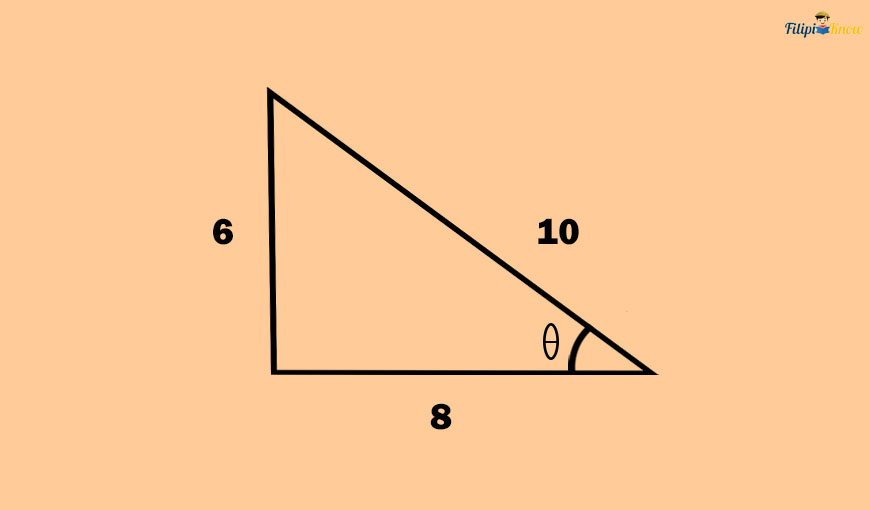
Sample Problem 1: Using the figure below, determine the sine, cosine, and tangent of the acute angle θ.
Solution:
Let us first define the opposite and the adjacent sides of the acute angle θ.
The opposite side of θ in the right triangle above is the side that measures six units. Meanwhile, the adjacent side of θ is the side that measures eight units.
The hypotenuse of the given right triangle is ten units long.
The value of the sine function is:
sin θ = opposite side/hypotenuse
sin θ = 6/10
sin θ = ⅗
The value of the cosine function is:
cos θ = adjacent side/hypotenuse
cos θ = 8/10
cos θ = ⅘
The value of the tangent function is:
tan θ = opposite side/adjacent side
tan θ = 6/8
tan θ = ¾
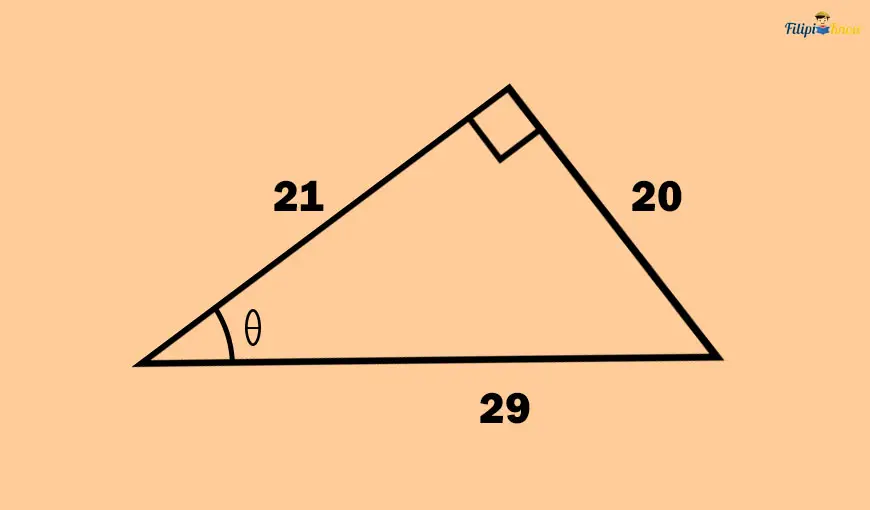
Sample Problem 2: Look at the given right triangle below. Determine the values of the sine, cosine, and tangent of the acute angle θ.
Solution:
Let us first define the opposite and adjacent sides of the acute angle θ.
The opposite side of θ in the right triangle above is the side that measures 20 units. Meanwhile, the adjacent side of θ is the side that measures 21 units.
The hypotenuse of the given right triangle is 29 units long. This is the side that is opposite the right angle.
The value of the sine function is:
sin θ = opposite side/hypotenuse
sin θ = 20⁄29
sin θ = 20⁄29
The value of the cosine function is:
cos θ = adjacent side/hypotenuse
cos θ = 21⁄29
cos θ = 21⁄29
The value of the tangent function is:
tan θ = opposite side/adjacent side
tan θ = 20⁄21
tan θ = 20⁄21
SOH-CAH-TOA
There is a fun way to remember the formulas or definitions of the right triangle’s sine, cosine, and tangent functions. All you have to do is to remember this acronym: SOH-CAH-TOA (read as “SO-KA-TOWA”).
SOH-CAH-TOA tells you that:
- SOH means “Sine is Opposite over Hypotenuse.”
- CAH means “Cosine is Adjacent over Hypotenuse.”
- TOA means “Tangent is Opposite over Adjacent.”
Some Things To Remember About the Sine, Cosine, and Tangent of Acute Angle θ
a. The tangent of acute angle θ is equal to the ratio of the sine of θ to the cosine of θ.
This means that if you try to divide the sine of θ by the cosine of θ, you will obtain the value of the tangent of θ.
Mathematically,
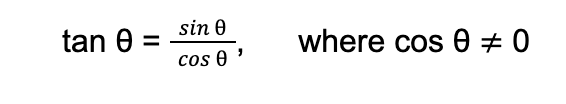
Sample Problem: Suppose the sin θ = 5⁄13 and cos θ = 12⁄13. Determine tan θ.
Solution: Again, tan θ equals sin θ over cos θ. Thus:
tan θ = sin θ/cos θ
tan θ = 5⁄13 ÷ 12⁄13
tan θ = 5⁄13 × 13⁄12
tan θ = 5⁄12
Thus, the answer is 5⁄12.
b. The value of the sine of θ and cosine of θ is always a positive number less than or equal to 1. Meanwhile, the value of the tangent of θ can be a number greater than 1.
For example, you will never see a sine θ = 3.5 value since this number is greater than 1.
c. The sum of the squares of the sine and cosine of θ equals 1.
(sin θ)2 + (cos θ)2 = 1
If you try to square both the values of the sine and cosine of θ and add them, it is certain that their sum will be equal to 1. This relationship between the squares of the sine and cosine of θ is one of the so-called Pythagorean identities in trigonometry.
Sample Problem: If p is an acute angle of a right triangle, determine the value of (sin p)2 in terms of cos p?
Solution: According to the Pythagorean identity discussed above, the sum of squares of the sine and the cosine of an acute angle of a right triangle equals 1. Thus, in our problem, we are assured that (sin p)2 + (cos p)2 = 1.
Hence, we have this equation:
(sin p)2 + (cos p)2 = 1
If we want to find the value of (sin p)2 in terms of cos p, we isolate (sin p)2 from the other terms in the equation above or let it be the only term on the left-hand side of the equation. Thus, by transposition method:
(sin p)2 + (cos p)2 = 1
(sin p)2 = -(cos p)2 + 1
As you can see, we’re able to express (sin p)2 in terms of cos p. So, the answer to the problem is:
(sin p)2 = -(cos p)2 + 1
Let us now discuss the remaining three trigonometric functions: cosecant, secant, and cotangent.
4. Cosecant
The cosecant of θ (abbreviated as “csc”) is the reciprocal of the sine of θ. This means that if the sine of θ is defined as the ratio of the length of the opposite side of θ to the hypotenuse, then the cosecant is defined as the ratio of the length of the hypotenuse to the length of the opposite side of θ.
Cosecant of θ = hypotenuse/opposite side
Thus, to find the cosecant of θ, you must first determine the opposite side of θ and its length. Once you have it, divide the hypotenuse length by the measurement of the opposite side.
You can also reciprocate the value of the sine of θ.
5. Secant
The secant of θ (abbreviated as “sec”) is the reciprocal of the cosine of θ. This means that if the cosine of θ is defined as the ratio of the length of the adjacent side of θ to the hypotenuse, then the secant is defined as the ratio of the length of the hypotenuse to the length of the adjacent side of θ.
Secant of θ = hypotenuse/adjacent side
Thus, to find the secant of θ, you must first determine the adjacent side of θ and its length. Once you have it, divide the length of the hypotenuse by the measurement of the adjacent side.
You can also reciprocate the value of the cosine of θ.
6. Cotangent
The tangent of θ (abbreviated as “cot”) is the reciprocal of the tangent of θ. This means that if the tangent of θ is defined as the ratio of the length of the opposite side of θ to the adjacent side of θ, then the cotangent is defined as the ratio of the length of the adjacent side of θ to the opposite side of θ.
Cotangent of θ = adjacent side/opposite side
Thus, to find the cotangent of θ, you must first determine the opposite and the adjacent sides of θ and their respective lengths. Once you have them, divide the length of the adjacent side by the length of the opposite side.
You can also reciprocate the value of the tangent of θ.
Notice that the last three trigonometric functions are just the reciprocal of the sine, cosine, and tangent functions.
Sample Problem: Determine the values of the cosecant, secant, and cotangent of θ in the right triangle below:
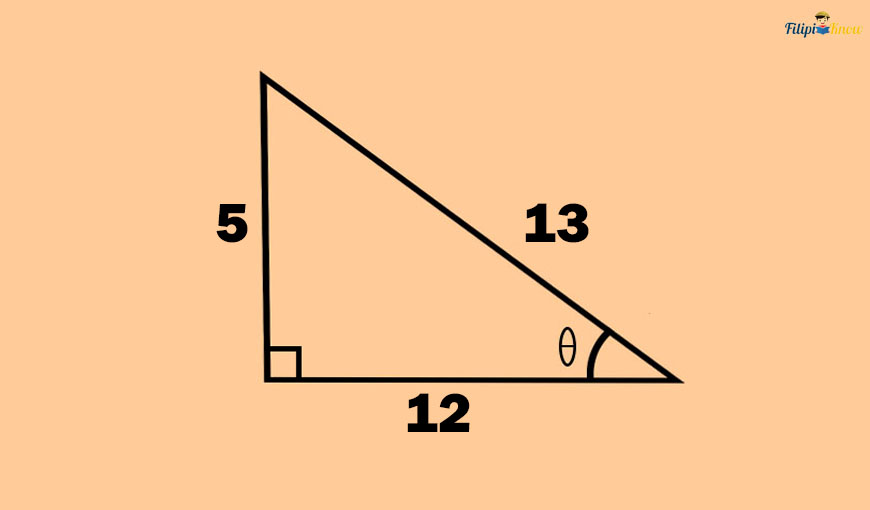
Solution: In the right triangle above, the opposite side of θ is five units long. Meanwhile, its adjacent side is 12 cm long. Lastly, the hypotenuse is 13 cm long.
Let us determine the values of the cosecant, secant, and cotangent of θ using the definitions we have provided above.
The value of the cosecant of θ is
cosecant of θ = hypotenuse/opposite side
csc θ = 13⁄5
csc θ = 13⁄5
The value of the secant of θ is
secant of θ = hypotenuse/adjacent side
sec θ = 13⁄12
sec θ = 13⁄12
The value of the cotangent of θ is
cotangent of θ = adjacent side/opposite side
cot θ = 12⁄5
cot θ = 12⁄5
Please take note that you can also derive the sine, cosine, and tangent values of the acute angle θ in the right triangle above, then take their reciprocals to obtain the values of the cosecant, secant, and cotangent, respectively.
For instance, the value of the sine of θ in the right triangle above is:
sin θ = opposite side/hypotenuse
sin θ = 5⁄13
We have obtained a value of 5⁄13 for sine θ. Since the cosecant of θ is the reciprocal of the sine of θ, then if sin θ = 5⁄13, csc θ = 13⁄5.
Trigonometric Values of the Special Angles
In our discussion of the right triangles, you have learned two types of special right triangles: the isosceles right triangle and the 30°-60°-90° right triangle.
The acute angles of these special right triangles provide us with special trigonometric function values. For these reasons, we call the interior angles of these special right triangles as special angles.
The special angles in trigonometry include the 45° angle, 30° angle, 60° angle, and 90° angle. Let us derive their respective trigonometric values in this section.
1. Trigonometric Values of the 45° Angle
Look at the given isosceles right triangle below. Recall that an isosceles right triangle has two acute interior angles with measurements of 45°.
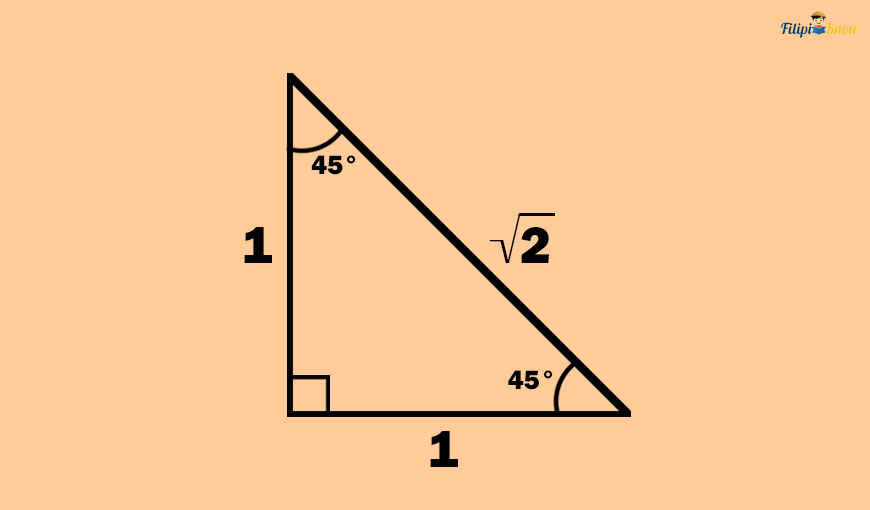
If the legs of the isosceles right triangle are 1 unit long, then the hypotenuse must be √2 units long due to the isosceles right triangle theorem.
Using the illustration above, we can derive the trigonometric values of the 45° angle (you can do it manually, but let me show it to you in the next paragraph).
The opposite side of the 45° angle is 1 unit long. The adjacent side of the 45° angle is also 1 unit in length. Lastly, the hypotenuse is √2 units long.
Using the definitions of trigonometric functions, you will obtain the following:
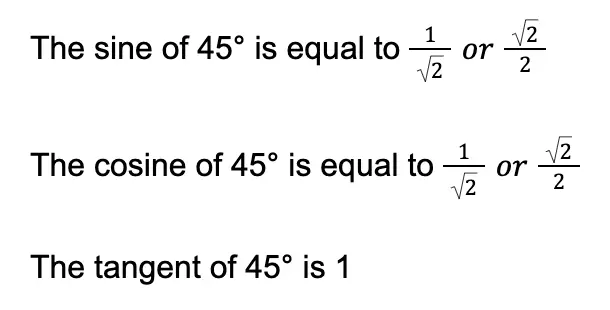
By reciprocating the three values above, we can obtain the remaining trigonometric values of the 45° angle.
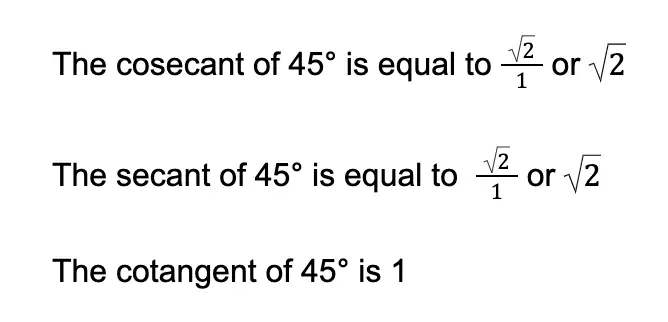
2. Trigonometric Values of the 30° Angle and the 60° Angle
We will derive the special trigonometric values of the 30° and 60° angles using the concepts of the 30° – 60° – 90° right triangle.
Let 1 unit be the length of the shorter leg of the 30°- 60°- 90° right triangle below. This means the longer leg must be √3 units long, and the hypotenuse must be two units long (according to the 30° – 60° – 90° right triangle theorem).
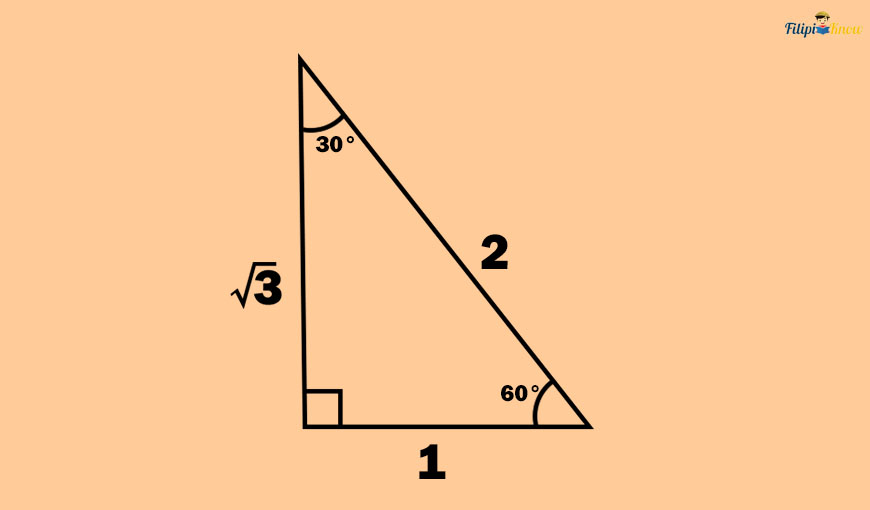
Let us first obtain the trigonometric values of the 30° angle. If we use the 30° angle as the reference, the opposite side will have a length of 1 unit. Meanwhile, the adjacent side will have a length of √3 units. The hypotenuse is still two units.
You can try obtaining the trigonometric values manually using the formulas we discussed earlier. But let me list down the trigonometric values of 30° below:
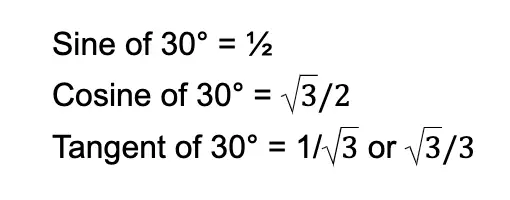
Obtaining the last three trigonometric functions is easy. All we have to do is to reciprocate the values above:
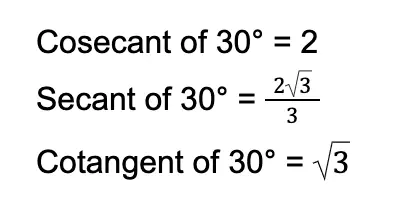
Meanwhile, if we let 60° be our reference angle, the opposite side will measure √3 units (the longer leg), and the adjacent side will measure 1 unit. Of course, the hypotenuse will still be two units long.
I have listed down the trigonometric values of the 60° angle. You can try obtaining these values manually using the given formulas for the trigonometric functions.
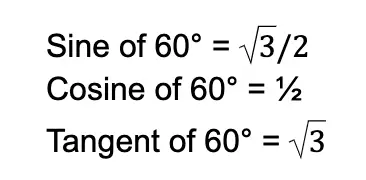
We reciprocate the values above to obtain the remaining three trigonometric values:
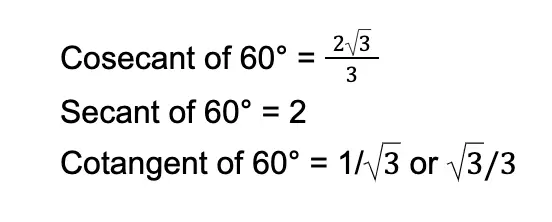
3. Trigonometric Values of the 90° Angle
The last special angle in our list is the 90° angle. Here are the special trigonometric values of this angle:
- Sine of 90° = 1
- Cosine of 90° = 0
- Tangent of 90° = undefined
Reciprocating the values above, we have the values for the cosecant, secant, and cotangent:
- Cosecant of 90° = 1
- Secant of 90° = 0
- Cotangent of 90° = 0
To summarize the trigonometric values of these special angles, we write them in the table below for your quick reference:
| 45° angle | 30° angle | 60° angle | 90° angle | |
| Sine (sin) | √2/2 | ½ or 0.5 | √3/2 | 1 |
| Cosine (cos) | √2/2 | √3/2 | ½ or 0.5 | 0 |
| Tangent (tan) | 1 | √3/3 | √2 | undefined |
| Cosecant (csc) | √2 | 2 | 2√3/3 | 1 |
| Secant (sec) | √2 | 2√3/3 | 2 | 0 |
| Cotangent (cot) | 1 | √3 | √3/3 | 0 |
I highly recommend memorizing the values in the table above for the trigonometric values of the special angles. However, if you suddenly forget the trigonometric value of a special angle while taking an exam, don’t fret because you can obtain it using the method I have presented above. Draw the special right triangle, put the appropriate measurements, determine the lengths of the opposite and adjacent sides, then derive the trigonometric functions.
I’m sure you have asked yourself this question: Why must I memorize these trigonometric values of special angles? It’s because there are problems in trigonometry where you can apply the trigonometric values of these special angles, and you will see them shortly in our next section.
Furthermore, you will reencounter this concept once you dive right into the Unit Circle, our next topic. So, it is advantageous that you know these special values.
More Trigonometric Functions Examples With Solution
Let us now apply the concepts of trigonometric functions and solve some problems involving them.
Sample Problem 1: A ladder leans against a wall measuring 10 meters high and forms a 30° angle from the ground. Determine the distance between the bottom of the ladder and the bottom of the wall.
Solution: Let us first illustrate the given problem above.
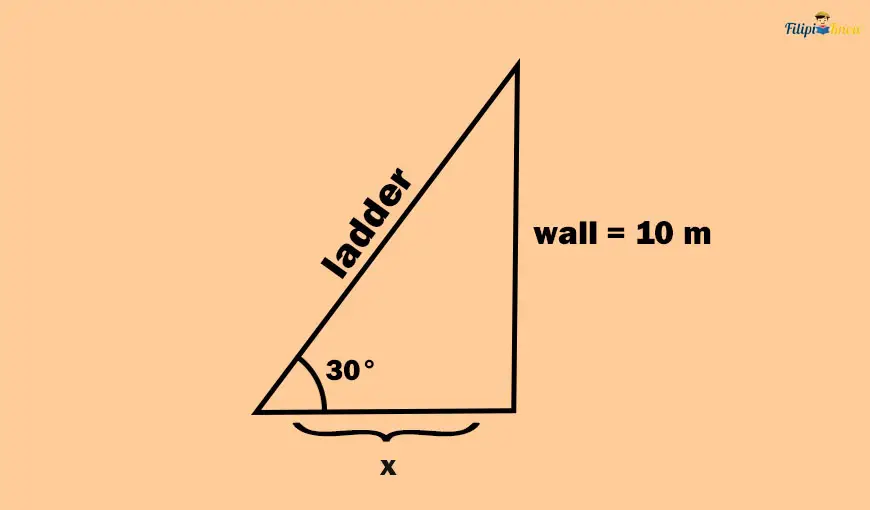
We aim to find the distance between the bottom of the ladder and the wall. We label that distance “x” in our illustration.
If you use 30° as our reference, the opposite side will be the wall measuring 10 meters high, while the adjacent side is the distance “x” in the figure or the distance between the bottom of the ladder and the bottom of the wall.
The only measurement we have is the height of the wall, which is the opposite side of our reference 30° angle. Recall that we are looking for the distance “x,” which is the adjacent side of our reference 30° angle. So, the opposite and adjacent sides are involved in our problem.
Which trigonometric function uses the opposite side and adjacent side? Yes, that’s the tangent and cotangent functions. But, we only need one of them, so let me use the tangent function.
Recall that tan θ = opposite side/adjacent side
Our θ = 30°, the opposite side is the wall measuring 10 meters high, and the adjacent side is the distance “x.”
So, we input these values into the equation above:
tan (30°) = 10/x
Here comes the application of the trigonometric values of the special angles. Do you still remember the value of the tangent of 30°?
Yes, that’s √3/3.
So, we replace tan(30°) with √3/3 in our equation above:

Thus, the distance “x” is equal to 10√3 cm.
Sample Problem 2: If the sin θ = 4⁄7, determine tan θ.
Solution: Recall that sin θ = opposite side/hypotenuse. Since sin θ = 4⁄7, we have opposite side = 4 and hypotenuse = 7.
How do we find the value of tan θ?
tan θ is mathematically defined as opposite side/adjacent side. We already have a value for the opposite side of four units derived from the given value of sine θ in the problem. The missing value is the one for the adjacent side.
This means we must compute the length or value of the adjacent side of θ.
Recall that by the Pythagorean theorem, the sum of the squares of the opposite side and the adjacent side equals the square of the hypotenuse. Mathematically:
(Opposite side)2 + (adjacent side)2 = (hypotenuse)2
Recall that we have opposite side = 4 and hypotenuse = 7. The missing number is the one for the adjacent side.
Let x be the length of the adjacent side.
Using the values we have, let us substitute them in the equation above:
(4)2 + (x)2 = (7)2
16 + x2 = 49
x2 = -16 + 49 Transposition method
x2 = 33
√x2 = √33 Take the square root of both sides of the equation
x = ±√33
We have computed two values for x, one is positive √33, and the other one is negative √33. We reject -√33 since we are looking for the length of the adjacent side (negative length is impossible). So, we will take x = √33 only.
Since x represents the adjacent side, the adjacent side is √33 units long.
We can now determine the value of tan θ.
tan θ = opposite side/adjacent side
We already have opposite side = 4 and adjacent side = √33.
Therefore, the value of the tangent of θ is:
tan θ = 4/√33
Rationalizing the denominator of the value above will give us the following:

Next topic: Unit Circle
Previous topic: Right Triangles
Return to the main article: The Ultimate Basic Math Reviewer
Download Printable Summary/Review Notes
Download Printable Flashcards
Test Yourself!
1. Practice Questions [Free PDF Download]
2. Answer Key [Free PDF Download]
3. Math Mock Exam + Answer Key
Written by Jewel Kyle Fabula
in College Entrance Exam, LET, NMAT, PMA Entrance Exam, Reviewers, UPCAT
Jewel Kyle Fabula
Jewel Kyle Fabula graduated Cum Laude with a degree of Bachelor of Science in Economics from the University of the Philippines Diliman. He is also a nominee for the 2023 Gerardo Sicat Award for Best Undergraduate Thesis in Economics. He is currently a freelance content writer with writing experience related to technology, artificial intelligence, ergonomic products, and education. Kyle loves cats, mathematics, playing video games, and listening to music.
Copyright Notice
All materials contained on this site are protected by the Republic of the Philippines copyright law and may not be reproduced, distributed, transmitted, displayed, published, or broadcast without the prior written permission of filipiknow.net or in the case of third party materials, the owner of that content. You may not alter or remove any trademark, copyright, or other notice from copies of the content. Be warned that we have already reported and helped terminate several websites and YouTube channels for blatantly stealing our content. If you wish to use filipiknow.net content for commercial purposes, such as for content syndication, etc., please contact us at legal(at)filipiknow(dot)net
