Solving Right Triangles

Right triangles are geometric figures that offer a variety of applications. It is widely used for construction purposes, navigation, approximation of measurement of tall structures, and a lot more. Furthermore, it allowed us to develop trigonometry, extensively used in other fields such as astronomy, physics, and engineering.
How can such a simple figure become so powerful that it changes the course of our planet? Learn more about this geometric plane figure and techniques for solving right triangles in this review.
Click below to go to the main reviewers:
Ultimate PMA Entrance Exam Reviewer
Table of Contents
What Are Right Triangles?: A Review
Recall that we can classify triangles according to interior angles. If the interior angles of a triangle are all acute, then we call it an acute triangle. If at least one interior angle is obtuse, we call it an obtuse triangle. Now, if a triangle has one 90° angle, it is a right triangle.
Essentially, right triangles contain a right-angle (90° angle) while the two interior angles are acute.
Parts of a Right Triangle
The longest side of a right triangle is called the hypotenuse. Meanwhile, the remaining shorter sides of the right triangle are called the legs.
To help you remember:
- Longest side ⇰ Hypotenuse
- Shorter sides ⇰ Legs
The small square that you can see between the legs of the right triangle indicates that the angle formed by the legs is a 90-degree angle. Once you see this “tiny square” inside a triangle, it gives you a hint that the triangle you are looking at is a right triangle.
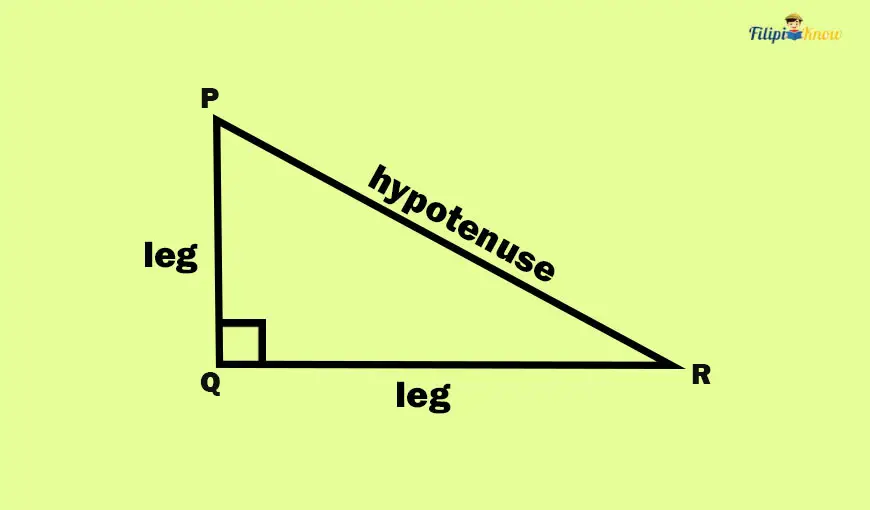
In the figure above, sides PQ and QR are the legs of the right triangle PQR, while side PR is the hypotenuse. Take note that the hypotenuse of a right triangle is always opposite to the right angle.
In a right triangle, the legs are perpendicular since they form a right angle. Hence, in the given figure above PQ ⊥ QR.
If the legs of the right triangle are congruent or equal in measurement, then that right triangle is called an isosceles right triangle. Meanwhile, if all sides of the right triangle have different measurements, it is a scalene right triangle.
Now that you know a right triangle’s legs and the hypotenuse, let us explore the theorem that shows the relationship among these parts.
Pythagorean Theorem
“The sum of the squares of the lengths of the legs of a right triangle on a flat surface is equal to the square of the length of its hypotenuse.”
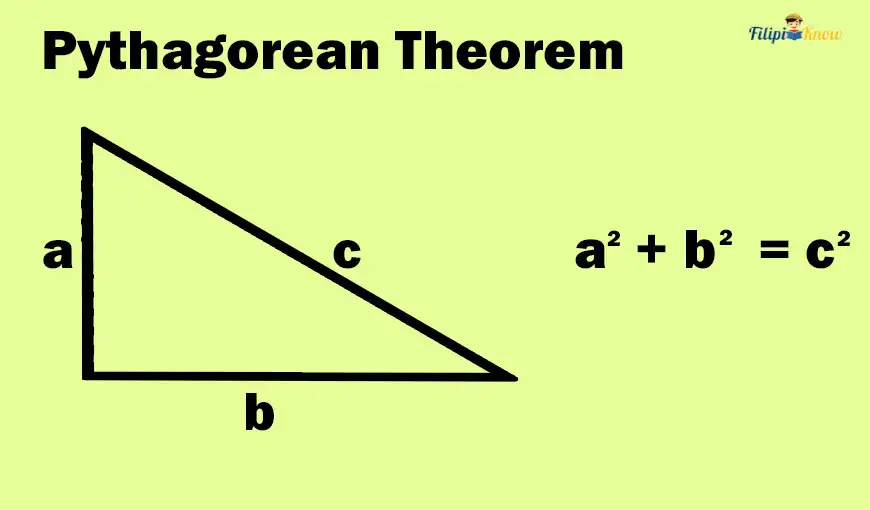
The Pythagorean theorem states that if you square the lengths of both legs of the right triangle and then add them, the result will be equivalent to the square of the length of the hypotenuse.
(Leg 1)2 + (Leg 2)2 = (Hypotenuse)2
To make the mathematical statement above easier to remember, we let a and b be the length of the legs and c be the hypotenuse of the right triangle. The Pythagorean theorem states that:
a2 + b2 = c2
This theorem is one of the most popular theorems in mathematics. It’s attributed to the Greek mathematician Pythagoras who proved this theorem hundreds of years ago. If you are interested in how this theorem has been proven throughout the years, you may watch this video from Ted-Ed.
Sample Problem 1: The right triangle below has legs measuring 4 cm and 3 cm. Determine how long its hypotenuse (or the longest side) is.
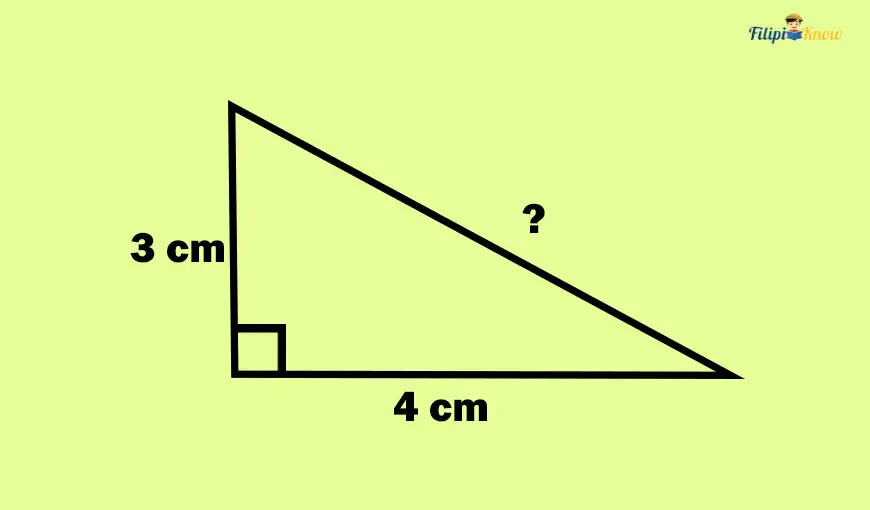
Solution: The Pythagorean theorem states that a2 + b2 = c2 where a and b are the legs while c is the hypotenuse.
We have a = 4 and b = 3. Using the Pythagorean theorem, let us solve for the hypotenuse c:
a2 + b2 = c2
(4)2 + (3)2 = c2 Substitute a = 4 and b = 3
16 + 9 = c2
25 = c2
√25 = √c² Take the square root of both sides of the equation
±5 = c
c = ±5
The values of c that we have obtained are 5 and -5. Recall that c represents the length of the hypotenuse of the right triangle. Thus, we must reject -5 since having a negative length of a right triangle is impossible. Thus, we will only take 5 as the value of c.
Hence, the hypotenuse of the right triangle is 5 cm.
Sample Problem 2: Look at the map shown below. How long is the shortest path from Helen’s house to the library?

Solution: The shortest path connecting Helen’s house and the library is the diagonal line connecting these two places. So, we draw a diagonal line that connects them.
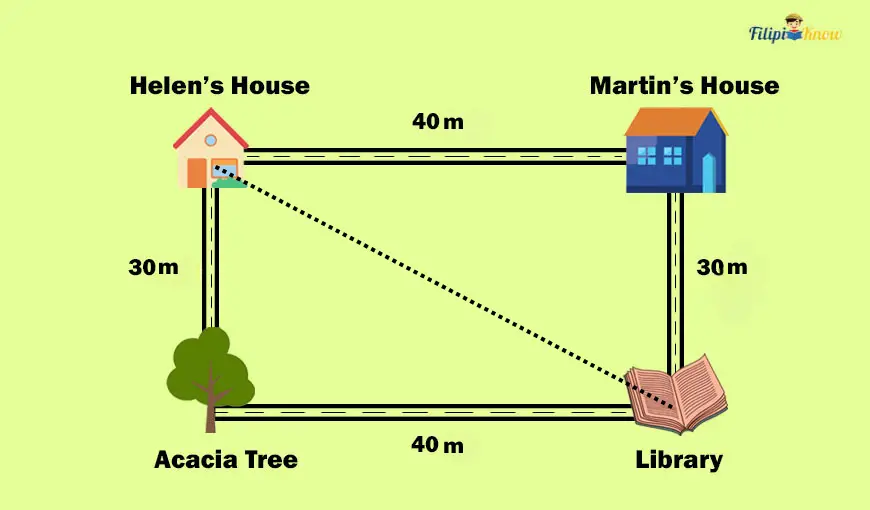
The length of the diagonal line that we draw is the distance of the shortest path from Helen’s house to the library.
Notice that we have created a right triangle as we draw this diagonal line between Helen’s house and the library. The legs are the road from Helen’s house to the Acacia tree and the road from the Acacia tree to the library.
And what is the hypotenuse? None other than the diagonal line representing the shortest path from Helen’s house to the library.
Since we have formed a right triangle, we can apply the Pythagorean theorem to find the length of this diagonal line. We have already defined the legs of this triangle in the previous paragraph. The diagonal line will serve as the hypotenuse of this right triangle.
Let us do the math now.
The legs have measurements of 30 m and 40 m. So, we have a = 30 and b = 40. We let c as the length of the hypotenuse of the right triangle.
Using the Pythagorean theorem:
a2 + b2 = c2
(30)2 + (40)2 = c2
900 + 1600 = c2
2500 = c2
c2 = 2500
√c² = √2500
c = ±50
We reject the negative value of c.
Thus, the hypotenuse of the right triangle we formed is 50. It means that the diagonal line we draw measures 50 m. Therefore, we conclude that the shortest path from Helen’s house to the library is 50 meters long (try computing the total distance of all possible paths from Helen’s house to the library, and you will discover that the shortest distance is indeed the one represented by the diagonal line).
Sample Problem 3: What is the measurement of the side AB in the right triangle below?
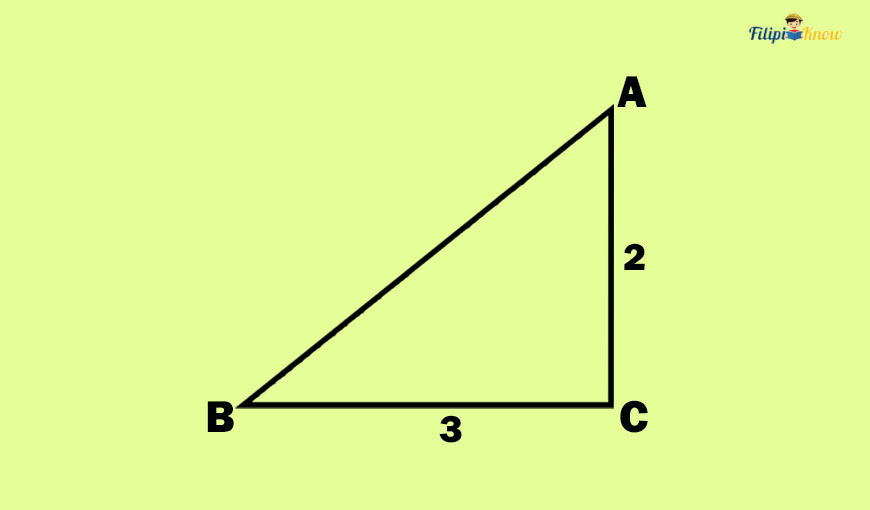
Solution: We have legs AC and BC that measure 2 and 3 units, respectively. Let us compute the hypotenuse AB using the Pythagorean theorem.
a2 + b2 = c2 The a and b are the legs, and c is the hypotenuse
(2)2 + (3)2 = c2 Substitute the values or measurement of the legs to a and b
4 + 9 = c2
13 = c2
c2 = 13 Symmetric property of equality
√c² = √13
c = ±√13
We reject the negative value.
Thus, the hypotenuse of the right triangle is √13 units.
Sample Problem 4: Determine the value of Q in the right triangle below.
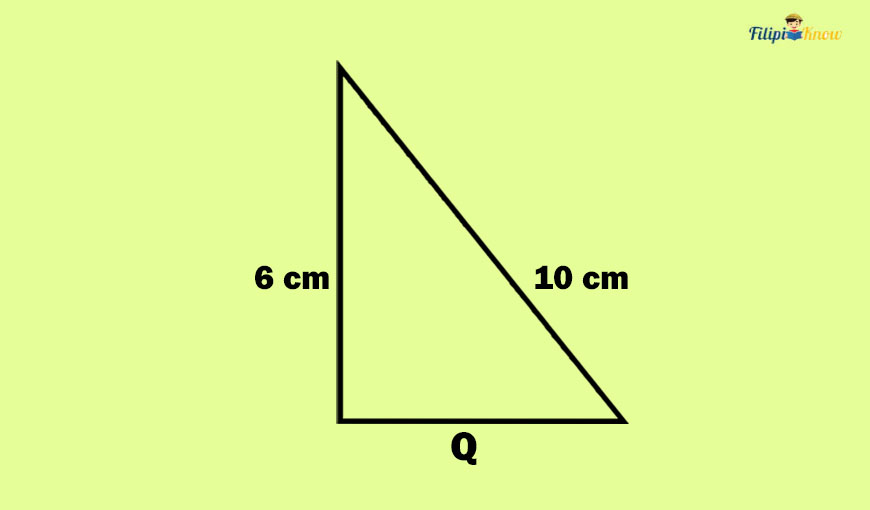
Solution: In the figure above, Q represents the measurement of a leg. The other leg of the right triangle measures 6 cm, while its hypotenuse is 10 cm.
To find the missing measurement of a leg of a right triangle, we can use the Pythagorean theorem and manipulate the equation we will form.
a2 + b2 = c2 where a and b are the legs and c is the hypotenuse
(6)2 + (Q)2 = (10)2 One of the legs is 6 cm while the hypotenuse is 10 cm
36 + Q2 = 100
Q2 = -36 + 100 Transposition method (we isolate b from the constants)
Q2 = 64
√Q² = √64
Q = ±8
We reject -8 and take Q = 8 only.
Therefore, the missing measurement of the leg of the right triangle is 8 cm long. And since Q represents the measurement of a leg of the right triangle, the value of Q must be 8 cm.
Pythagorean Triples
Pythagorean triples are three positive whole numbers that satisfy the Pythagorean theorem.
The smallest Pythagorean triples are 3, 4, and 5. Notice how they satisfy the Pythagorean theorem:
If we let a = 3, b = 4, and c = 5:
a2 + b2 = c2
(3)2 + (4)2 = (5)2
9 + 16 = 25
25 = 25
Both sides are equal; therefore, 3, 4, and 5 are Pythagorean triples.
Now, let’s try 1, 2, and 3. Are these numbers Pythagorean triples?
Let a = 1, b = 2, and c = 3
a2 + b2 = c2
(1)2 + (2)2 = (3)2
1 + 4 = 9
5 ≠ 9
1, 2, and 3 failed to satisfy the Pythagorean theorem, so they are not triples.
Some common Pythagorean triples are the following:
- 3, 4, and 5
- 5, 12, and 13
- 7, 24, and 25
- 8, 15, and 17
- 11, 60, and 61
You can try it and confirm that these triples are all Pythagorean triples.
How can we get Pythagorean triples?
If you take the multiples of the triples listed above, you will still obtain a Pythagorean triple.
For instance, 5, 12, and 13 is a Pythagorean triple. If we multiply these three numbers by 4, we have 20, 48, and 52; these new triples are also Pythagorean triples.
Sample Problem: Is 27, 36, and 45 a Pythagorean triple?
Solution: Yes, because 27, 36, and 45 are derived by multiplying each of 3, 4, and 5, which are Pythagorean triples, by 9.
Converse of the Pythagorean Theorem
Again, the Pythagorean theorem tells us that in a right triangle, the sum of the squares of the lengths of legs is equal to the square of the length of the hypotenuse:
a2 + b2 = c2
The converse of the Pythagorean theorem tells us that if the square of the length of the longest side of the triangle is equal to the sum of the squares of the lengths of the remaining shorter sides, then the triangle formed is a right triangle.
Once we show that the condition above was satisfied, the triangle formed is a right triangle.
What if, for instance, the conditions of the converse of the Pythagorean theorem are unsatisfied?
We have two possible cases:
Case 1: If the square of the longest side is greater than the sum of the squares of the shorter sides of the triangle or c2 > a2 + b2 (where a and b are shorter sides and c is the longest side). In this case, we have an obtuse triangle.
Case 2: If the square of the triangle’s longest side is less than the sum of the squares of the shorter sides or c2 < a2 + b2, then we have an acute triangle.
So, to summarize:
If a and b are the shorter sides of a triangle and c is its longest side:
- If c2 = a2 + b2, then we have a right triangle
- If c2 > a2 + b2, then we have an obtuse triangle
- If c2 < a2 + b2, then we have an acute triangle
Sample Problem 1: The shorter sides of a triangle have measurements of 2 cm, 4 cm, and 5 cm. Determine what type of triangle this is.
Solution: The square of the length of the longest side (the one that measures 5 cm) is (5)2 = 25.
The sum of the squares of the lengths of the shorter sides (the remaining sides) is:
(2)2 + (4)2 = 4 + 16 = 20
Notice that the square of the length of the longest side is greater than the sum of the squares of the lengths of the shorter sides or c2 > a2 + b2. Thus, the triangle is obtuse.
Sample Problem 2: Triangle PQR has the following measurements: PQ = 5 cm, QR = 2 cm, and PR = 7 cm. Determine whether the triangle is acute, right, or obtuse.
Solution: The triangle’s longest side is PR, which measures 7 cm. Its square is (7)2 = 49.
The sum of the squares of the lengths of the shorter sides PQ and QR is:
(5)2 + (2)2 = 25 + 4 = 29
Notice that the square of the length of the longest side is greater than the sum of the squares of the lengths of the shorter sides or c2 > a2 + b2. Thus, triangle PQR is an obtuse triangle.
Special Right Triangles
In the previous sections, you have learned how special right triangles are because of their wonderful characteristics described by the Pythagorean theorem. But did you know that there are special right triangles? This special plane figure has some types that are considered more special!
There are two types of special right triangles: the isosceles right triangles (or the 45° – 45° – 90° right triangle) and the 30° – 60° – 90° degree right triangles.
Let us talk about these special right triangles in this section.
1. Isosceles Right Triangles (45° – 45° – 90° Right Triangle)
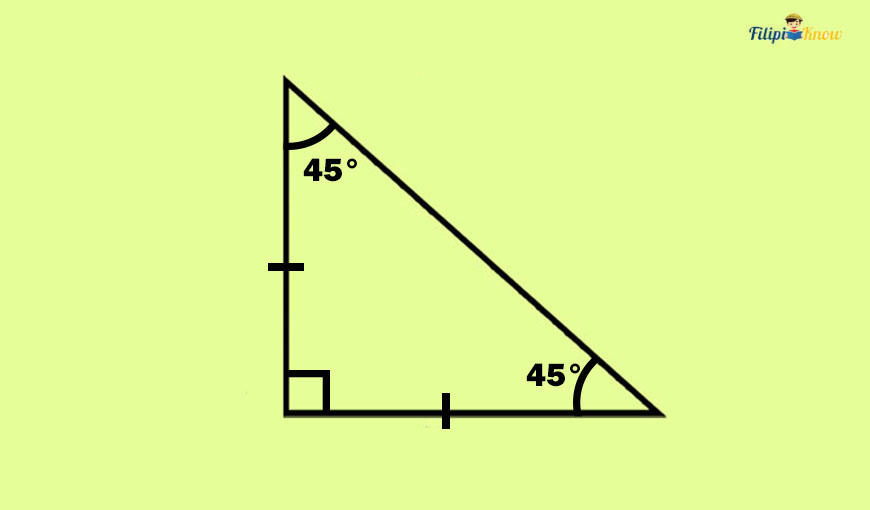
An isosceles right triangle is a right triangle such that its legs are congruent or have the same measurement. In an isosceles right triangle, the acute interior angles near the hypotenuse have degree measurements of 45°. This is why we call isosceles right triangles 45° – 45° – 90° right triangles.
What makes isosceles right triangles special?
In an isosceles right triangle, the length of the hypotenuse is √2 times longer than the measurement of a leg. Thus, you can determine the hypotenuse of the right triangle simply by multiplying the measurement of a leg by √2. No need to use the Pythagorean theorem! Can you imagine how quick and easy it is?
We formally state this property above as a theorem:
Isosceles Right Triangle Theorem
“If a right triangle is an isosceles right triangle (or 45°- 45°- 90° right triangle), then the hypotenuse is √2 times as long as the leg.”
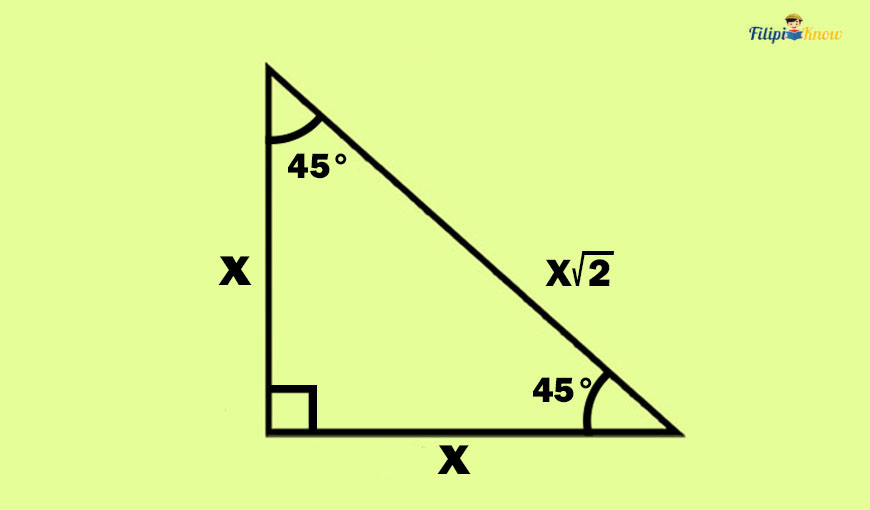
Sample Problem 1: Determine the measurement of the hypotenuse of the right triangle below.
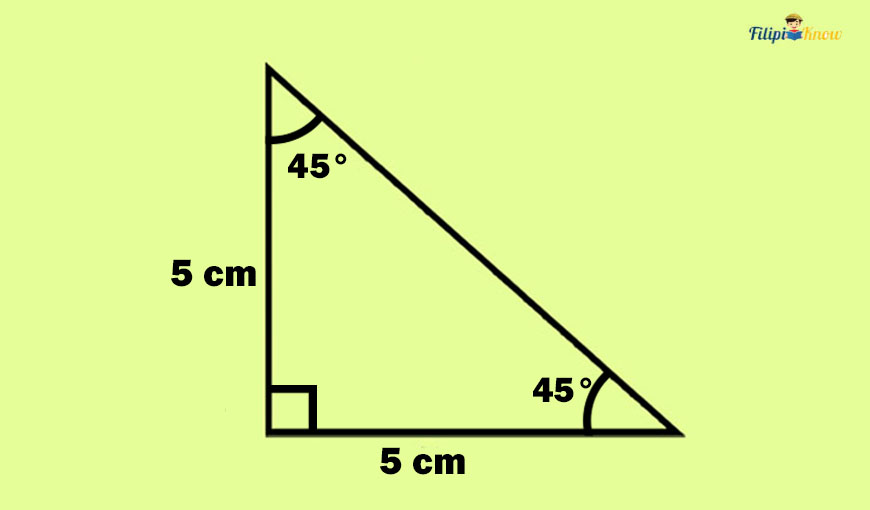
Solution: Since the given right triangle is an isosceles right triangle, we can multiply the leg measurement by √2 to obtain the hypotenuse. Thus, if the measurement of the leg is 5 cm, then the hypotenuse is simply 5√2 cm long.
Sample Problem 2: Determine how long a square’s diagonal is with a side measuring 2 meters.
Let us draw this square and its diagonal.
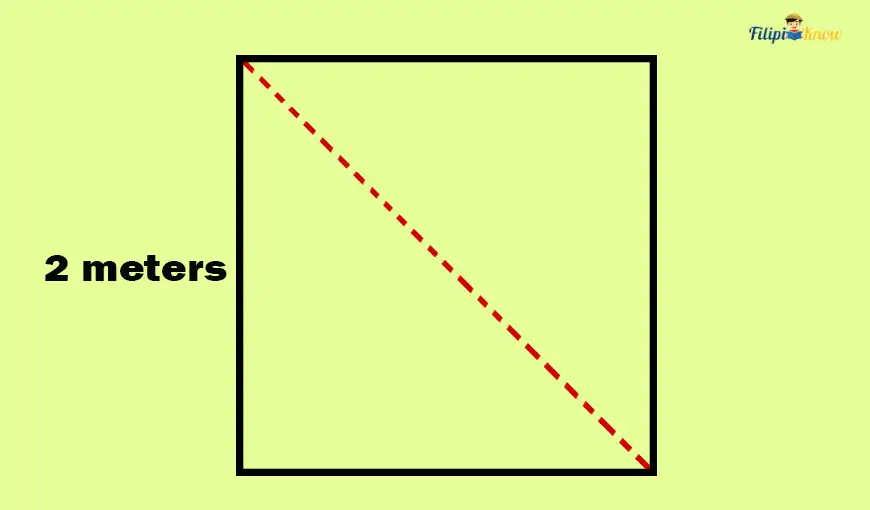
Solution: As we draw the square’s diagonal, we have formed a right triangle such that the legs are the sides and the hypotenuse is the diagonal. Interestingly, the right triangle formed is an isosceles right triangle since the legs are 2 meters long.
Thus, the hypotenuse of this isosceles right triangle we form is 2√2 meters. Since the hypotenuse of this isosceles right triangle is also the square’s diagonal, the diagonal is 2√2 meters long.
In the previous example, we have derived a practical way to measure a square’s diagonal, given only the square’s side. The square’s diagonal is simply the measurement of the side times √2. This fantastic concept was a direct consequence of the isosceles right triangle theorem.
Diagonal of a square = s√2
where s is the measurement of a side.
Sample Problem 3: The right triangle below has a hypotenuse with a length of 10 cm. Determine the length of a leg of the right triangle.
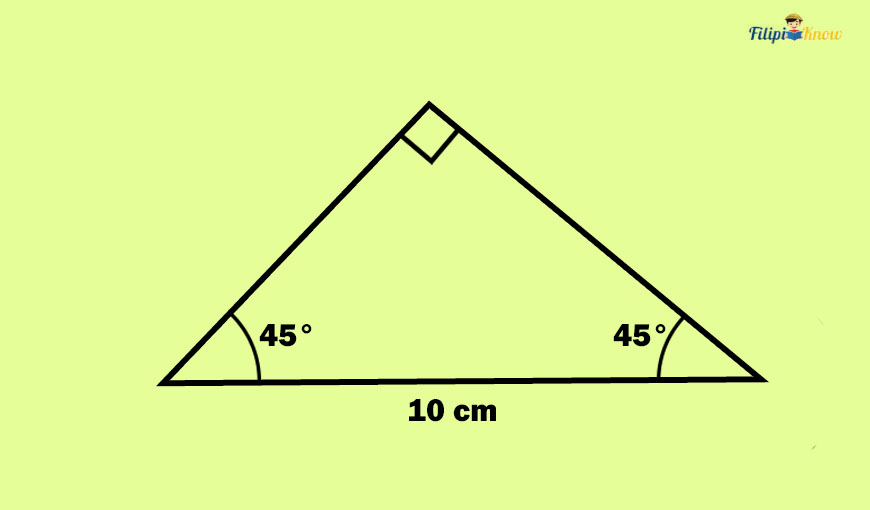
Answer: Although the right triangle above seems peculiar from the right triangles we have encountered earlier, it is still a right triangle because it has a right angle.
Anyway, the right triangle above is an isosceles right triangle because of the two 45-degree angles you can see near the hypotenuse with a length of 10 cm.
How do we find the measurement of a leg?
According to the isosceles right triangle theorem, the hypotenuse is √2 times as long as the leg. Thus, the measurement of a leg can be derived if we divide the measurement of the hypotenuse by √2.
Thus, the measurement of the leg of the isosceles right triangle below is again just 10 divided by √2 :
Measurement of the leg = 10 ÷ √2
We can compute the measurement of the leg as follows:
10 ÷ √2 = 10⁄√2
Notice that we have a radical in the denominator, so we need to rationalize it by multiplying both the numerator and the denominator by √2:
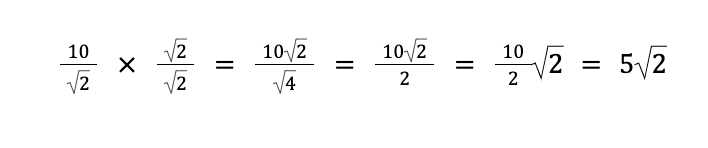
Thus, the leg measures 5√2 cm.
2. 30° – 60° – 90° Right Triangle
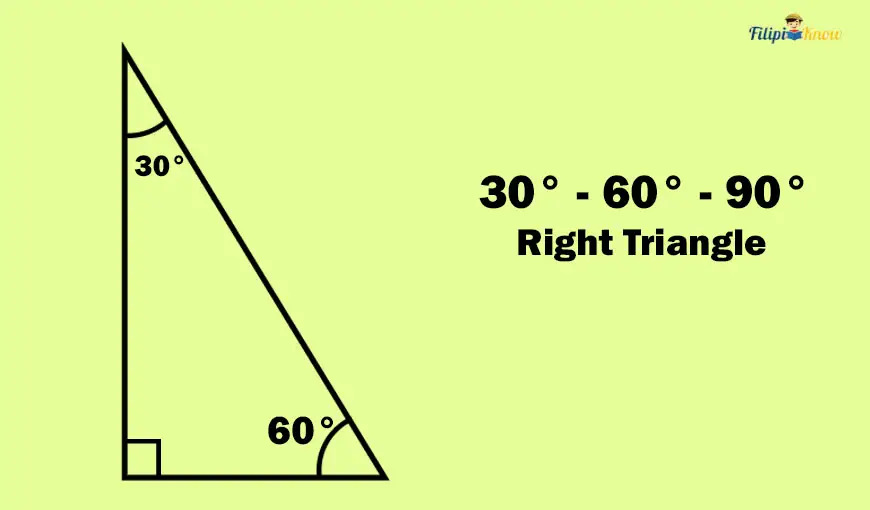
A 30° – 60° – 90° right triangle is another type of special right triangle. Unlike the previous special right triangle we have discussed, the 30° – 60° – 90° right triangle has no congruent sides. Furthermore, its acute interior angles have different measurements. One is a 30° angle, while the other is a 60° angle.
The side of the 30° – 60° – 90° right triangle that is opposite the 30° angle is the shorter leg. Meanwhile, the side opposite the 60° angle is the longer leg. Of course, the longest side is still the hypotenuse opposite the right angle.
Again,
- The side opposite the 30-degree angle = shorter leg
- The side opposite the 60-degree angle = longer leg
- Longest side = hypotenuse

30° – 60° – 90° Right Triangle Theorem
“In a 30° – 60° – 90° right triangle, the hypotenuse is twice as long as the shorter leg. Meanwhile, the longer leg is √3 times longer than the shorter side.”
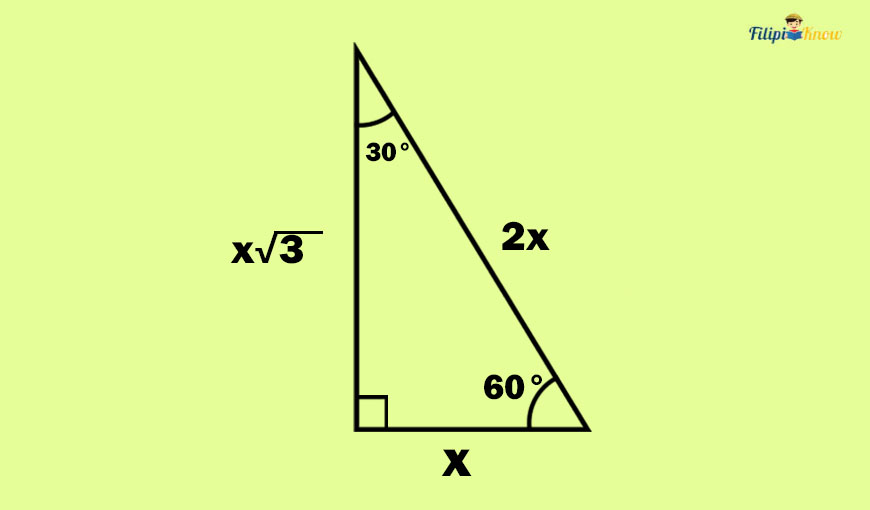
In this kind of special right triangle, the hypotenuse measurement can be obtained by simply doubling (or multiplying by 2) the length of the shorter side. Meanwhile, the measurement of the longer leg can be obtained by multiplying the length of the shorter leg by √3.
In symbols, if x is the measurement of the shorter leg, then:
- Longer leg = x√3
- Hypotenuse = 2x
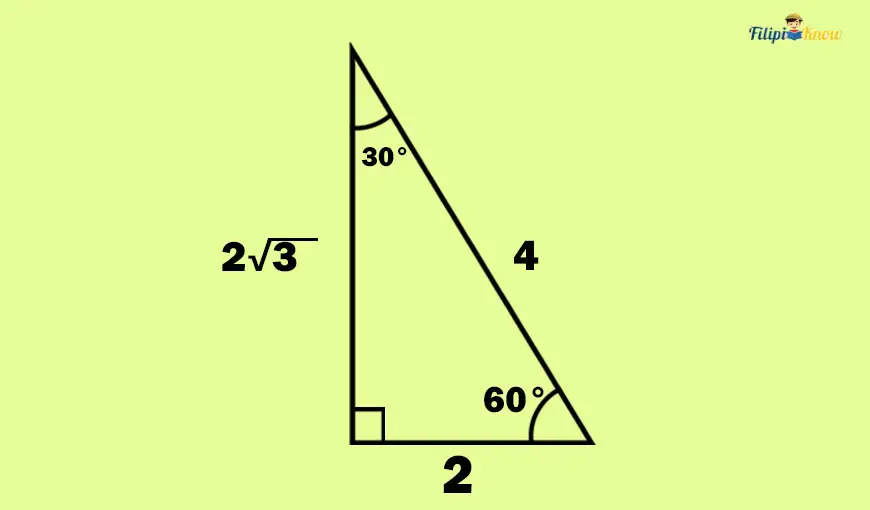
Look at the 30° – 60° – 90° right triangle below. Its shorter leg measures 2 cm. The longer leg is 2√3 cm. Notice that the longer leg length is just the measure of the shorter leg times √3. Meanwhile, its hypotenuse is 4 cm long, just twice the shorter leg’s measure.
Sample Problem 1: Determine the x and y values in the right triangle below.
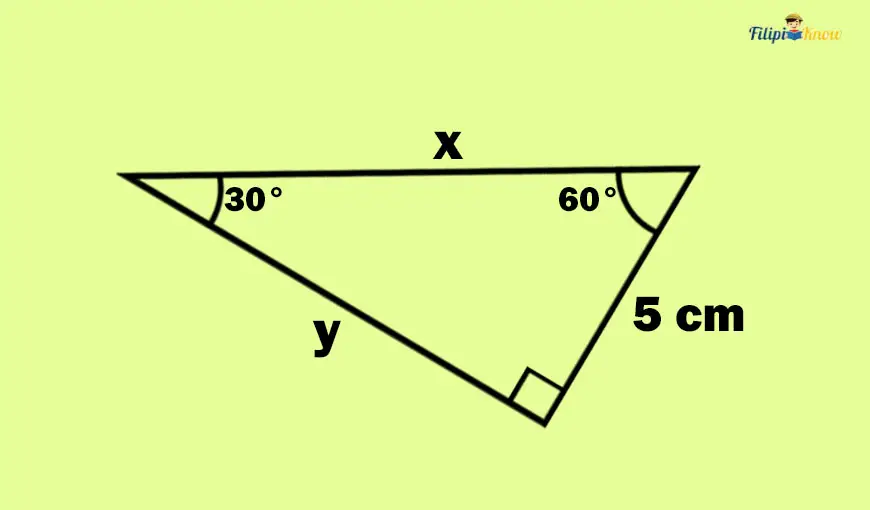
Solution: Obviously, the given right triangle above is a 30° – 60° – 90° right triangle because of the existence of 30-degree and 60-degree angles inside it.
To make our computation easy, let us determine first the shorter leg. Recall that the shorter leg is the leg that is opposite to the 30-degree angle. If you take a look at the given image, the shorter leg is the one that has a measure of 5 cm.
Meanwhile, the longer leg is the side with the letter y as the measurement since this side is opposite the 60-degree angle.
Lastly, x represents the right triangle’s hypotenuse or the longest side.
So, we have the following given:
- Shorter leg = 5 cm
- Longer leg = y
- Hypotenuse = x
In a 30° – 60° – 90° right triangle, the hypotenuse length is just twice the length of the shorter leg. Since the shorter leg is 5 cm, the hypotenuse is just 5(2) = 10 cm long. Since x represents the hypotenuse of the right triangle, then x = 10 cm.
Meanwhile, the length of the longer leg is √3 times as long as the length of the shorter leg. Thus, if the shorter leg is 5 cm long, the longer leg is 5(√3) = 5√3 cm long. Since y represents the longer leg, then y = 5√3 cm.
Therefore, x = 10 cm while y = 5√3 cm.
Sample Problem 2: Determine the measurement of side p in the figure below:
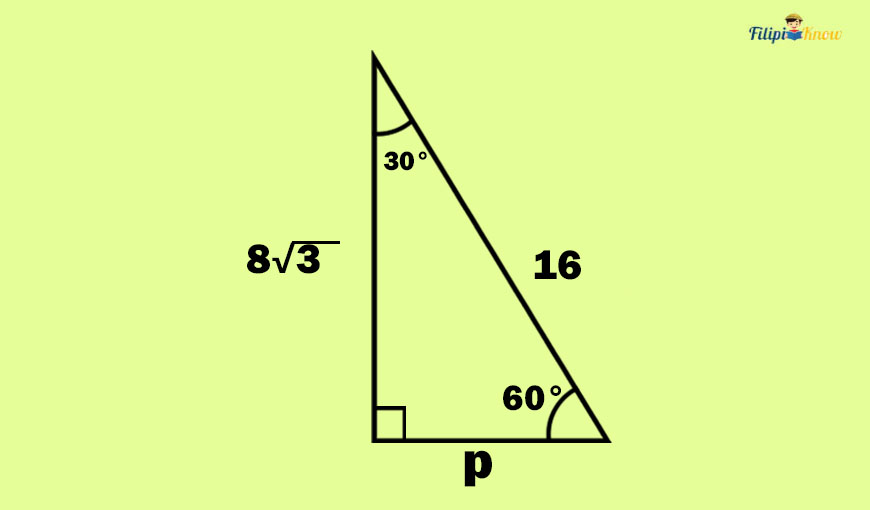
Solution: First, we must identify what p represents in the figure above.
The figure above is a 30° – 60° – 90° right triangle.
The side with the letter p is the shorter leg of this 30° – 60° – 90° right triangle because this side is opposite the 30-degree angle. Meanwhile, the side with a length of 8√3 is the longer leg since this side is opposite the 60-degree angle.
Recall that in a 30° – 60° – 90° right triangle, the longer leg is √3 times longer than the shorter leg. Now that we have 8√3 as the longer leg, how do we derive the length of the shorter leg?
Yes, we have to divide 8√3 by √3:
8√3 ÷ √3 = 8
Thus, the shorter leg is 8 cm long. The measurement of the shorter leg is represented by p; therefore, p = 8 cm.
Solving Word Problems Involving Right Triangles
It’s now time to apply what you have learned about right triangles. Let us try to solve some word problems involving right triangles by using the Pythagorean theorem and the characteristics of the special right triangles.
Sample Problem 1: The diagonal of a rectangle is 35 cm long. If the width of the rectangle is 21 cm long, determine the perimeter of the rectangle.
Solution: The problem above can be solved easily if we create a diagram to illustrate it.
So, we have a diagonal that is 35 cm long and a width of 21 cm long:
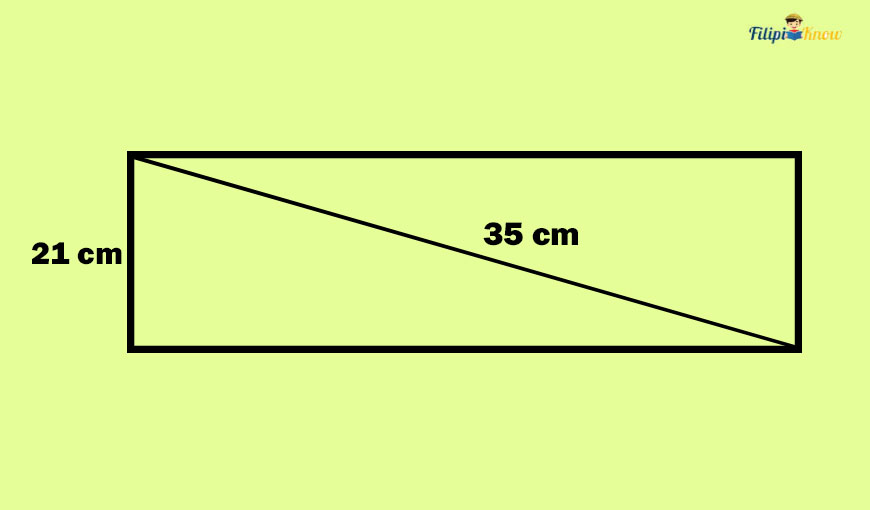
The problem requires us to find the perimeter of the rectangle above. Recall that the formula for the perimeter of a rectangle is P = 2l + 2w where l is the length and w is the rectangle’s width. We already have the width of the rectangle. Unfortunately, the problem didn’t provide us with the length.
So, our goal is to look for the length of the rectangle, and then once we find it, we will compute the perimeter of the rectangle.
How can we find the length of the rectangle using the given values in the problem?
If you look again at the given rectangle above, the diagonal formed a right triangle with the diagonal as the hypotenuse and the width as one of the legs of the right triangle. This implies that the other leg of this right triangle must be the length of the rectangle. Since the length of the rectangle is unknown, we let x be the length of the rectangle.
We can now determine the length of the rectangle using the Pythagorean theorem.
The Pythagorean theorem states that a2 + b2 = c2 where a and b are the legs of the right triangle and c is the hypotenuse. Since our legs are the length and the width of the rectangle, then we have the following:
- a = x (this is the value of our unknown length)
- b = 21 (this is the given width of the rectangle)
Furthermore, since the rectangle’s diagonal is the hypotenuse, we have c = 35.

Let us now do the math and compute for the length (which is x):
a2 + b2 = c2
(x)2 + (21)2 = (35)2 Using the values we have set above
x2 + 441 = 1,225
x2 = -441 + 1,225 Transposition method
x2 = 784
√x² = √784 Take the square root of both sides
x = ±28
We will disregard the negative value of x and take x = 28 only.
Since x represents the length of the rectangle, then the length of the rectangle is 28 cm.
We can now determine the perimeter of the rectangle since we have the length and width measurements.
We have length = 28 cm and width = 21 cm, so:
P = 2l + 2w
P = 2(28) + 2(21)
P = 56 + 42
P = 98
Thus, the perimeter of the rectangle is 98 cm.
Sample Problem 2: A ladder measuring 5 meters long is leaning against a brick wall. The ladder makes a 60° angle from the ground. Determine how tall the brick wall is.
Solution: Let us try to illustrate this problem first.
So, we have a 5-meter ladder leaning against a wall. That ladder makes a 60-degree angle from the ground. Our task is to find the height of the brick wall.

Looking closely at our illustration above, we formed a right triangle such that the ground and the wall are the legs while the ladder is the hypotenuse. Furthermore, since the ladder created a 60-degree angle, it is a 30°-60°-90° right triangle. Hence, the other acute angle in the figure must be a 30° angle.
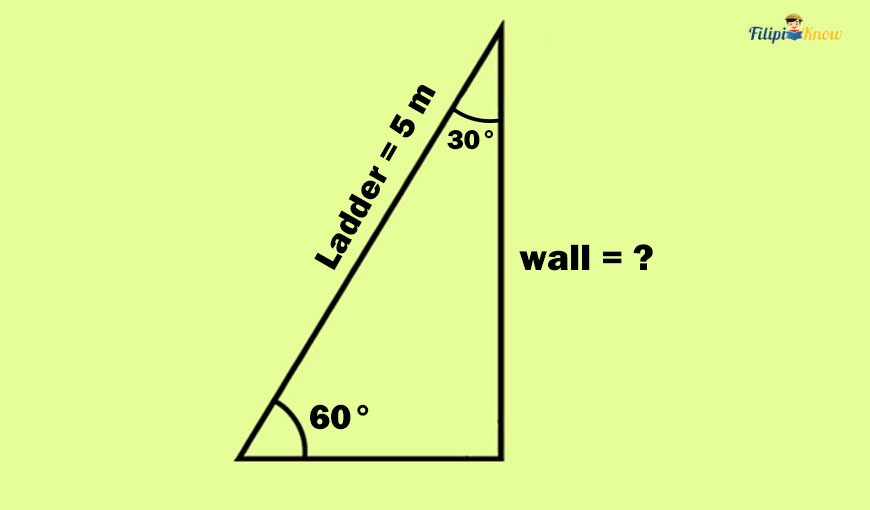
Let us determine this right triangle’s shorter and longer leg.
The shorter leg is the side that is opposite the 30° angle. Thus, the shorter leg is the ground between the ladder and the wall. Meanwhile, the longer leg is the side opposite the 60° angle. Thus, the longer leg is the wall or the height of the wall.
Meanwhile, the ladder is the hypotenuse of this right triangle.
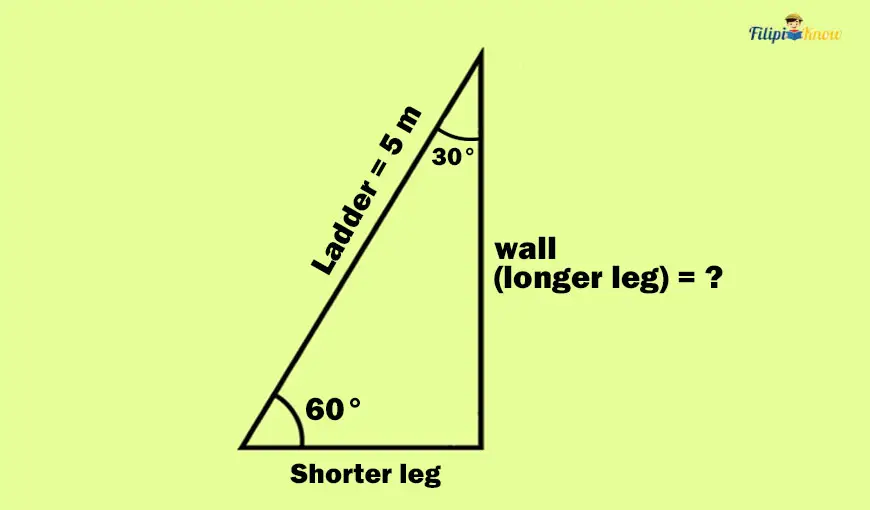
Thus, to find the height of the wall, we need to find the longer leg of this right triangle.
We can start by determining the shorter leg first. According to our previous theorem about 30°- 60°- 90° triangles, the hypotenuse is twice as long as the shorter leg. Since the hypotenuse of the right triangle in our illustration is the ladder, which is 5 meters long, the shorter leg is simply 5⁄2 or 2.5 meters long.
Therefore, the shorter leg is 2.5 meters long.
The longer leg is √3 times as long as the shorter leg. This means that the measurement of the longer leg is just the product of √3 and the measurement of the shorter leg.
Since we have computed that the shorter leg’s measurement is 2.5 meters long, the longer leg’s measurement must be 2.5√3 meters.
Recall that the height of the wall in the problem is equivalent to the longer leg of the right triangle formed. Thus, the height of the wall in the problem is 2.5√3 meters.
Sample Problem 3: A right triangle is inscribed in a circle. Suppose the legs of the right triangle are both 12 cm long. Determine the radius of the circle.
Solution: Based on our previous discussion about circles, the right triangle’s hypotenuse will be the circle’s diameter when a right triangle is inscribed in a circle.
Thus, to find the circle’s radius in this problem, we can solve for the hypotenuse of the right triangle first since it is also the circle’s diameter. Afterward, we will divide the result by 2 to obtain the radius (since the circle’s diameter equals twice the circle’s radius).
The given legs of the right triangle are both 12 cm. Hence, we can conclude that this right triangle is an isosceles right triangle. According to the isosceles right triangle theorem, the length of the hypotenuse of an isosceles right triangle is √2 times as long as the length of the legs. Thus, if the legs of the right triangle in the problem are 12 cm long, the hypotenuse must be 12√2 cm long.
Again, since the hypotenuse is also the diameter of the circle, then the diameter of the circle is 12√2 cm. To obtain the radius, we divide 12√2 by 2:
12√2 ÷ 2 = 6√2
Thus, the radius of the circle is 6√2 cm long.
Remember the concepts you have learned about right triangles in this review because these will be your primary tools to understand the trigonometric functions we will discuss in the next review.
Next topic: Six Trigonometric Functions
Previous topic: Circles
Return to the main article: The Ultimate Basic Math Reviewer
Download Printable Summary/Review Notes
Download Printable Flashcards
Test Yourself!
1. Practice Questions [Free PDF Download]
2. Answer Key [Free PDF Download]
3. Math Mock Exam + Answer Key
Written by Jewel Kyle Fabula
in College Entrance Exam, LET, PMA Entrance Exam, Reviewers, UPCAT
Jewel Kyle Fabula
Jewel Kyle Fabula graduated Cum Laude with a degree of Bachelor of Science in Economics from the University of the Philippines Diliman. He is also a nominee for the 2023 Gerardo Sicat Award for Best Undergraduate Thesis in Economics. He is currently a freelance content writer with writing experience related to technology, artificial intelligence, ergonomic products, and education. Kyle loves cats, mathematics, playing video games, and listening to music.
Copyright Notice
All materials contained on this site are protected by the Republic of the Philippines copyright law and may not be reproduced, distributed, transmitted, displayed, published, or broadcast without the prior written permission of filipiknow.net or in the case of third party materials, the owner of that content. You may not alter or remove any trademark, copyright, or other notice from copies of the content. Be warned that we have already reported and helped terminate several websites and YouTube channels for blatantly stealing our content. If you wish to use filipiknow.net content for commercial purposes, such as for content syndication, etc., please contact us at legal(at)filipiknow(dot)net
