Factors and multiples are two essential concepts in the study of arithmetic. These concepts allow us to understand significant mathematical ideas such as prime numbers, GCF, LCM, etc.

In this review, we will talk about factors and multiples and the mathematical concepts behind them. 

Click below to go to the main reviewers:

Ultimate UPCAT Reviewer

Ultimate NMAT Reviewer

Ultimate Civil Service Exam Reviewer

Ultimate PMA Entrance Exam Reviewer

Ultimate PNP Entrance Exam Reviewer

Ultimate LET Reviewer

   

Part I: Factors

What are the factors?

Factors are the numbers we multiply to obtain another number (or the product). For example, when 9 and 5 are multiplied together, the result is 45. Therefore, 9 and 5 are factors of 45.

Here’s another interesting fact: A factor of a number can divide the number without a remainder. For example, we already know that 5 is a factor of 45. If we divide 45 by 5, as in 45 ÷ 5 = 9, there’s no remainder!

Let’s have a few more examples:

Example 1: What are the factors of 21?

Solution: Note that:

• 1 x 21 = 21
• 3 x 7   = 21

Thus, 1, 3, 7, and 21 are factors of 21.

Example 2: What are the factors of 150?

Solution: Note that:

• 1 x 150 = 150
• 2 x 75 = 150
• 3 x 50 = 150
• 5 x 30 = 150
• 6 x 25 = 150

And so on…

Therefore, 1, 2, 3, 4, 5, 6, 25, 30, 50, 75, and 150 are some of the factors of 150.

Are negative numbers a factor of a number?

Yes, they are! For example, – 3 × – 2 = 6. Since when you multiply – 3 by -2, the result is 6, then – 3 and – 2 are factors of 6. Hence, a negative number can also be a factor.

 

Prime and Composite Numbers

We can classify whole numbers based on the number of factors they have. Whole numbers can either be prime numbers or composite numbers.

What is a prime number?

A prime number is a whole number greater than one with only two factors: 1 and itself. For example, 3 is a prime number since it has only two factors which are one and itself (i.e., 3). You cannot think of other factors of 3 aside from 1 and 3.

What is a composite number?

A composite number is a whole number that has more than two factors. For example, 6 is a composite number since it has more than two factors which are 1, 2, 3, and 6. 

Remember that 1 is neither a prime number nor a composite number. 

Example: Which of the following numbers is prime?

2, 10, 19, 145

Solution:

Let us list all factors of each given number and determine whether they are prime or not:

For 2: 

• 2 x 1 = 2

Factors of 2: 1, 2

Since 2 has only two factors, one and itself, then 2 is a prime number.

For 10:

• 1 x 10 = 10
• 2 x 5 = 10

Factors of 10: 1, 2, 5, 10

Since 10 has more than two factors, 10 is not a prime number.

For 19:

• 1 x 19 = 19

Factors of 19: 1, 19

Since 19 has only two factors, one and itself, then 19 is a prime number.

For 145:

• 1 x 145 = 145
• 5 x 29 = 145

Factors: 1, 5, 29, 145

Since 145 has more than two factors, 145 is not a prime number.

Thus, only 2 and 19 are the prime numbers.

 

Prime Factorization

Prime factorization is the process of expressing a composite number as a product of its prime factors. Simply put, you will determine which prime numbers that when multiplied together, will give you the original number. 

For example, the prime factorization of 24 is 2 × 2 × 2 × 3 = 24, or when written with exponents, 2³ × 3.= 24. Notice that the factors used in the prime factorization of 24 are all prime numbers (2 and 3).

Another example: The prime factorization of 105 is 3 × 5 × 7 = 105. Notice that 105 is expressed as a product of prime numbers (which are 3, 5, and 7).

You are now introduced to the concept of prime factorization of a number. However, how do we find it? How can we determine the prime factorization of a number?

One method you can use is prime factorization using the factor tree.

 

Prime Factorization Using the Factor Tree

A factor tree is a diagram that can be used to find the factors of any number, then the factors of those numbers, and so on, until we can’t factor anymore. The ends of the factor tree are all of the prime factors of the original number.

When you perform this method, your computation will look like a tree! 

Let’s determine the prime factorization of 24 using the factor tree.

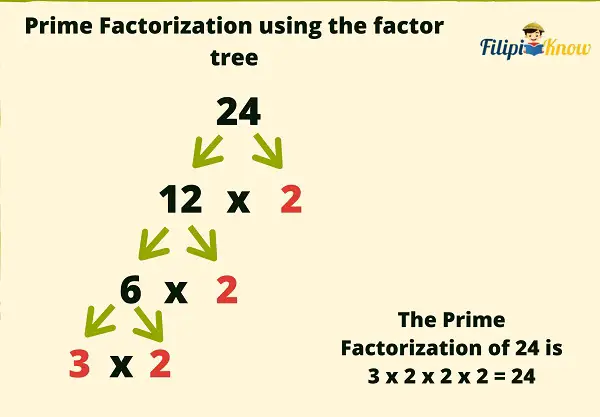
12 and 2 are factors of 24. Notice that 2 has no factors besides one and itself, so we stop there. On the other hand, we can still look for the factors of 12.

6 and 2 are factors of 12. We can still look for factors of 6 since it is a composite number.

3 and 2 are factors of 6. Note that both 3 and 2 do not have factors aside from 1 and themselves (they are prime numbers), so we can already stop with these numbers.

We collect all the ends of the tree (numbers that are colored red) as they are the prime factors of 24. Finally, we express 24 as a product of these prime factors.

Hence, the prime factorization of 24 is 3 x 2 x 2 x 2 = 24 which we can also express with exponents as 3 x 2³ = 24

Example 1: Determine the prime factorization of 36 using a factor tree.

Start by thinking of any factors of 36. In this case, let us use 18 and 2 since 18 x 2 = 36. 

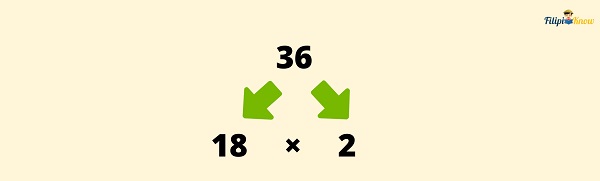
2 is a prime number, so we stop on that part. However, 18 is a composite number. This means that we can still factor it out. We think again of any factors of 18. This time let us use 9 and 2 since 9 x 2 = 18.

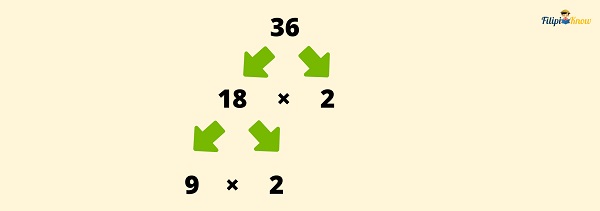
9 is a composite number, so we can still factor it out. We think again of any factors of 9. This time, let us use 3 and 3 since 3 x 3 = 9.

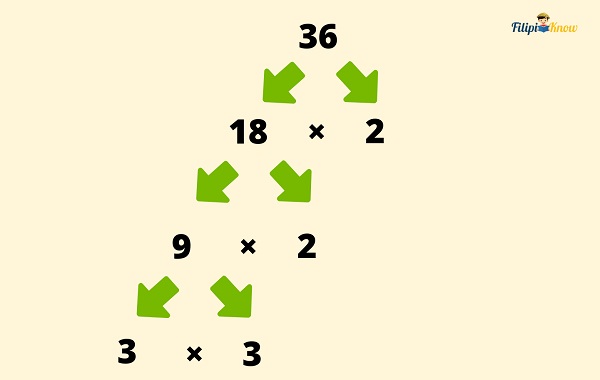
We collect all the ends of our factor tree (red-colored numbers). These are the prime factors of 36. We express 36 as a product of these prime factors.

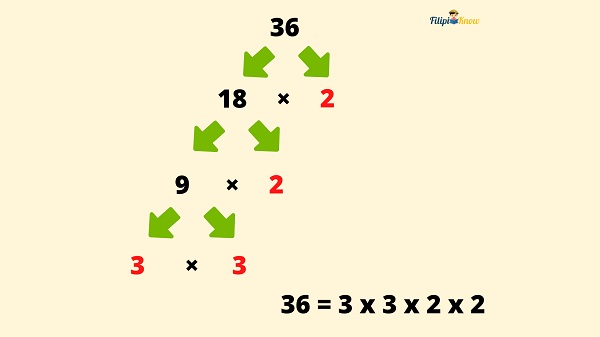
Therefore, the prime factorization of 36 is 3 x 3 x 2 x 2 = 36, or if written with exponents, 3² x 2² = 36

You have already learned what factors, prime numbers, composite numbers, and prime factorization are. Our next section will apply these concepts to determine the Greatest Common Factor of two numbers.

 

Greatest Common Factor

The Greatest Common Factor (GCF) is the largest common factor of given numbers. GCF is an essential tool in arithmetic because we use it to simplify fractions to their lowest terms.

One of the common methods to determine the GCF of two numbers is by listing their factors and determining the largest common factor from the list. Let’s try this method for our example below.

1. How to find the GCF of given numbers through the listing method

Example 1: Determine the GCF of 8 and 12.

Solution: Let us list all of the factors of 8 and 12:

• Factors of 8:  1, 2, 4, 8
• Factors of 12: 1, 2, 3, 4, 6, 12

Our list above shows that the common factors are 1, 2, and 4.

However, GCF must be the largest common factor. We already know that the common factors are 1, 2, and 4. Which of these common factors is the largest? It’s 4.

Thus, the GCF of 8 and 12 is 4.

Example 2: What is the GCF of 15 and 25?

Solution: Let us list all of the factors of 15 and 25:

• Factors of 15: 1, 3, 5, 15
• Factors of 25: 1, 5, 25

Based on the list above, the only common factor is 5. Therefore, it is also the largest common factor or GCF of 15 and 25. 

Thus, the GCF of 15 and 25 is 5.

The listing method seems to be a good method to find the GCF. However, it is not that convenient to use if the given numbers have plenty of factors. Listing a lot of factors will make our computation more tedious and time-consuming.

Another method can be used to determine the GCF of given numbers. This method uses prime factorization to find the GCF. 

2. How to find the GCF using the prime factorization method

To find the GCF of given numbers using the prime factorization method, you can follow these steps:

1. Determine the prime factorization of the given numbers (i.e., use factor trees).
2. Express the numbers as a product of their prime factors.
3. Match the prime factors vertically.
4. Bring down the common prime factors for each column. Do not bring down those in the columns where the factors are different.
5. Multiply the numbers you brought down. The result is the GCF.

Let us use this method to determine the GCF of 56 and 108.

Example: Use the prime factorization method to find the GCF of 54 and 108.

Solution:

1. Determine the prime factorization of the given numbers (i.e., use factor trees).

We apply the technique discussed in the previous section to perform the prime factorization of 56 and 108.

2. Express the numbers as a product of their prime factors.

From the abovementioned factor trees, we can express 56 and 108 as products of their prime factors. We rearrange the factors so that the same factors are vertically aligned. 

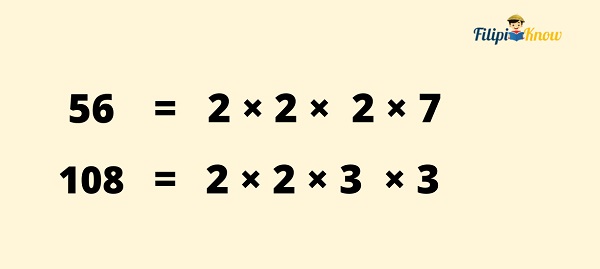
3. Match the prime factors vertically.

We match the common prime factors vertically using blue rectangles. We will not put a blue rectangle on a column where the prime factors are different.

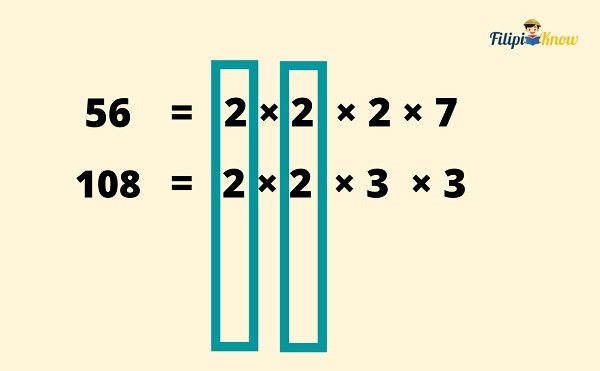
4. Bring down the common prime factors for each column. Do not bring down those in the columns where the factors are different.

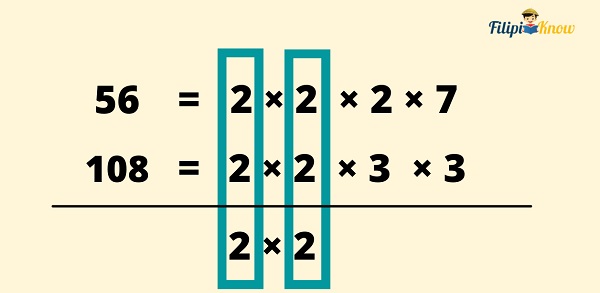
5. Multiply the numbers you brought down. The result is the GCF.

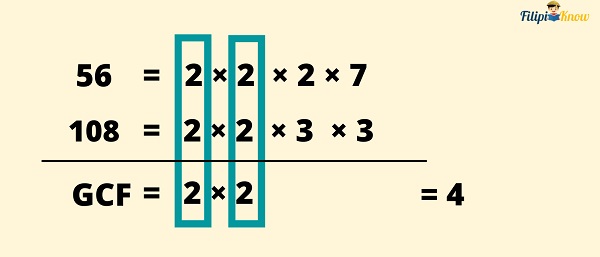
Therefore, using the prime factorization method, the GCF of 54 and 108 is 4.

 

Part II: Multiples

What are multiples?

A multiple is a result when we multiply a number by an integer. 12 is a multiple of 6 because when six is multiplied by the integer 2, the result is 12. Can you think of other multiples of 6?

Example 1: Provide five multiples of 10.

Solution: To find five multiples of 10, we must multiply ten by five different integers. For example:

10 × 1 = 10

10 × 3 = 30

10 × – 5 = – 50

10 × – 8 = – 80

10 × 140 = 1400

Hence, 10, 30, – 50, – 80, and 1400 are some of the multiples of 10.

Example 2: What are the first three positive multiples of 4?

Solution: Since we are now required to find the first three positive multiples of 4, we need to multiply four by the first three positive integers:

4 × 1 = 4

4 × 2 = 8

4 × 3 = 12

Thus, the first three positive multiples of 4 are 4, 8, and 12.

Example 3: How many multiples of 5 are between 14 and 21?

Solution: Note that the numbers 15 and 20 which are between 14 and 21, are multiples of 5 since

5 × 3 = 15 and 5 × 4 = 20. That is 15 and 20 results when five is multiplied by integers 3 and 4, respectively.

Thus, between 14 and 21, there are two multiples of 5.

 

Least Common Multiple (LCM)

The Least Common Multiple is the smallest whole number multiple of two or more numbers. Like the GCF, LCM is also used in some operations on fractions. Let’s give a simple example to help you understand what LCM is.

Example: Suppose you list the multiples of 2 and 3 from the least to the greatest value.

• Multiples of 2: 2, 4, 6, 8, 10, 12 …
• Multiples of 3: 3, 6, 9, 12, 15, …

Can you tell from the list which are the common multiples of 2 and 3?

Solution: Clearly, the common multiples of 2 and 3 are 6 and 12.

Now, you might notice that 6 is the smallest common multiple between 2 and 3. Therefore, 6 is the Least Common Multiple of 2 and 3.

Based on our example above, the Least Common Multiple is the smallest common multiple between given numbers.

1. How to find the LCM using the listing method

One of the common ways to find the LCM of two numbers is by listing the factors of the given numbers.  We already used this method for our example above, through which we could find the LCM of 2 and 3. Let’s use this method again to find the LCM of 5, 10, and 25.

Determining the LCM using the listing method seems to be a cakewalk. But what if I ask you to find the LCM of 130 and 300? The listing method appears to be inconvenient in this case. 

When the listing method becomes a tedious way of finding the LCM, use the prime factorization method instead.

2. How to find the LCM using prime factorization

To find the LCM of given numbers using prime factorization, follow these steps:

1. Determine the prime factors of the given numbers (using the factor tree).
2. Express the given numbers as the product of their prime factors.
3. Match the prime factors vertically.
4. Bring down the prime factors in each column.
5. Multiply the factors to obtain the LCM.

Let’s use prime factorization to find the LCM of 130 and 300.

Example: Determine the LCM of 130 and 300.

Solution:

1. Determine the prime factors of the given numbers (using the factor tree).

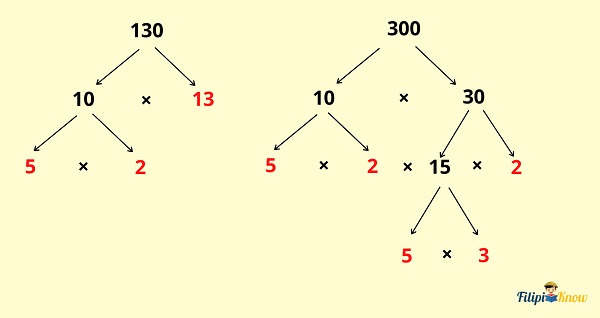
The ends (red-colored numbers) of the respective factor trees of 130 and 300 are their prime factors. We will use these prime factors for our next step.

2. Express the given numbers as the product of their prime factors.

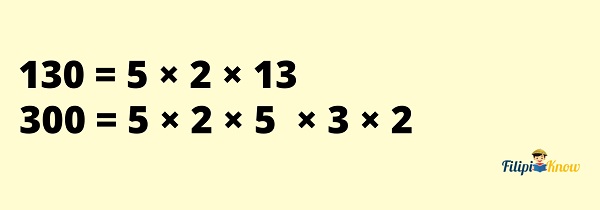
3. Match the prime factors vertically.

We match common prime factors vertically using the red rectangles. We leave the space blank if a prime factor has no “partner” to the other number.

4. Bring down the prime factors in each column.

Bring down the common prime factors in each column. In our illustration above, we bring down every common prime factor on each red rectangle.

5. Multiply the factors to obtain the LCM.

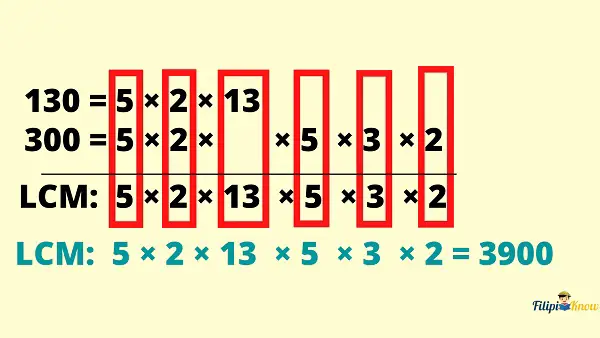
The last step is to multiply the common prime factors we have brought down from step 4. The resulting number is the Least Common Multiple (LCM).

Therefore, the LCM of 130 and 300 is 3900.

 

Next topic: Divisibility Rules

Previous topic: PEMDAS (Order of Operations)

Return to the main article: The Ultimate Basic Math Reviewer

 

Download Printable Summary/Review Notes

Download Printable Flashcards

Test Yourself!

1. Practice Questions [Free PDF Download]

2. Answer Key [Free PDF Download]

3. Math Mock Exam + Answer Key