Tasty pizza, magnificent roofs, and timeless pyramids: What’s common among these three?

Yes, they are all triangles! 

With their simple form consisting of three sides, triangles are one of the essential elements in geometry. Mathematicians’ fascination with these figures paved the way for numerous engineering, architecture, and navigation developments.

Using this reviewer, you can refresh your knowledge of triangles, their classification, properties, and valuable theorems.

Click below to go to the main reviewers:

Ultimate UPCAT Reviewer

Ultimate PMA Entrance Exam Reviewer

Ultimate LET Reviewer

Classification of Triangles

We all know that triangles are three-sided polygons with three angles. Let us start our discussion of triangles with their classification. We can classify triangles according to their interior angles or sides. 

1. Classification of Triangles According to Angles

We can classify triangles according to the measurement of their interior angles.

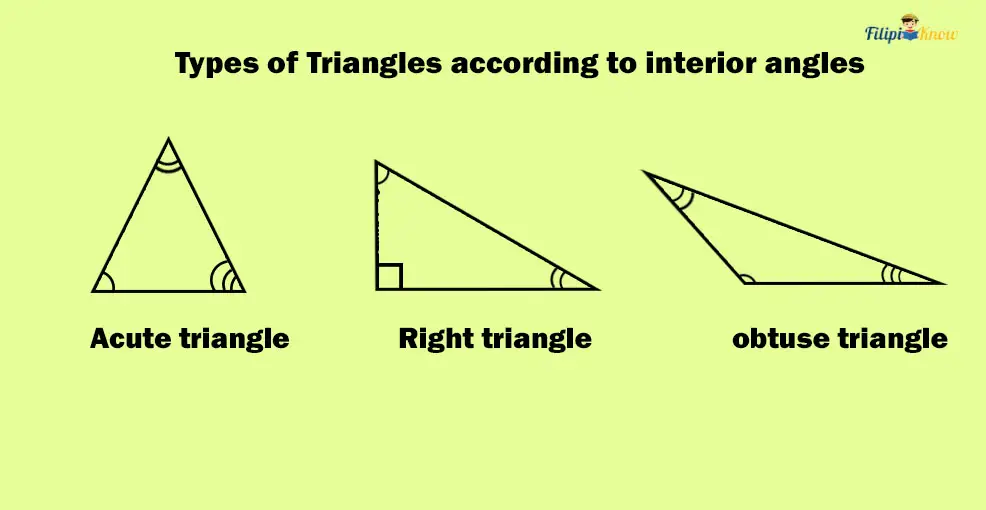
a. Acute Triangle

A triangle is acute if all of its interior angles are acute. This means that all of the interior angles of an acute triangle have a measurement between 0 degrees to 90 degrees.

b. Right Triangle

A right triangle has precisely one interior angle, a right angle (90° angle), and two interior angles are acute angles.

Right triangles are of great importance in geometry (and trigonometry). It is the subject of the famous mathematical theorem called the Pythagorean theorem. That’s why we must dedicate a separate discussion to this particular type of triangle. 

c. Obtuse Triangle

An obtuse triangle has precisely one obtuse interior angle, and two interior angles are acute.

2. Classification of Triangles According to Sides

If we classify triangles according to their sides, we will have three types of triangles: scalene, isosceles, and equilateral.

a. Scalene Triangle

A scalene triangle has all of its sides non-congruent. This means that all sides of a scalene triangle have different measurements. 

b. Isosceles Triangle

An isosceles triangle has two congruent sides. This means that two sides of an isosceles triangle have equal measurement or length. 

c. Equilateral Triangle

An equilateral triangle has congruent sides. This is the opposite of a scalene triangle. 

Congruent Triangles

Two triangles are congruent if all their corresponding sides and angles are equal. For instance, take a look at the given image below:

AB is congruent to its corresponding side DE; AC is congruent to its corresponding side DF; and BC is congruent to its corresponding side EF. Furthermore, all the corresponding angles of the triangles are equal in degree measurement. Therefore, triangles ABC and DEF are congruent triangles.

1. Corresponding Sides of Triangles

Look at the given triangles below. These triangles are named Triangle ABC and Triangle DEF.

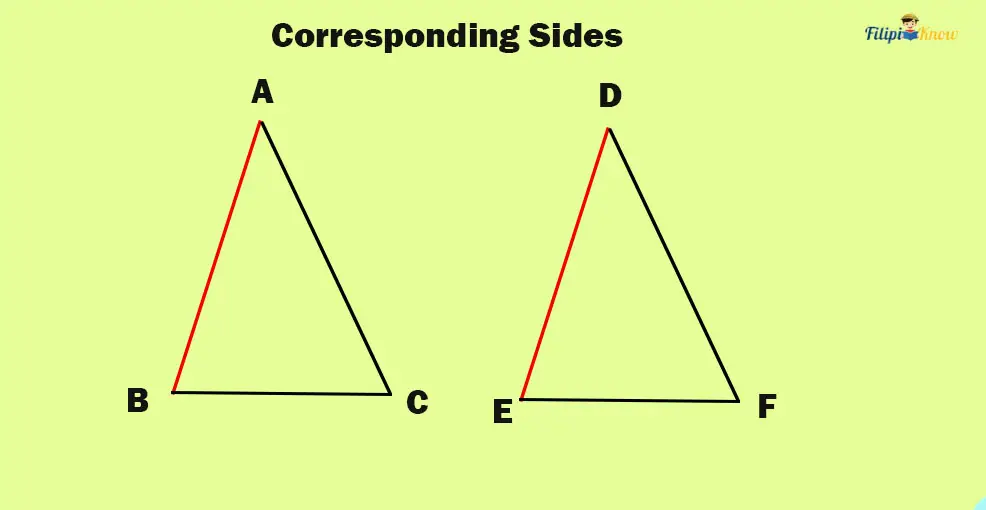
Note that side AB of triangle ABC is in the same position as side DE of triangle DEF. Thus, we call them corresponding sides. 

Therefore, the corresponding sides of triangles are the sides of triangles located in the same location. 

2. Corresponding Angles of Triangles

The corresponding angles of triangles are similar to the concept of corresponding sides. Corresponding angles of triangles are the angles of triangles located in the same location. 

In the figure below, angles 1 and 4 are corresponding angles. Similarly, angles 2 and 5 are also corresponding angles.

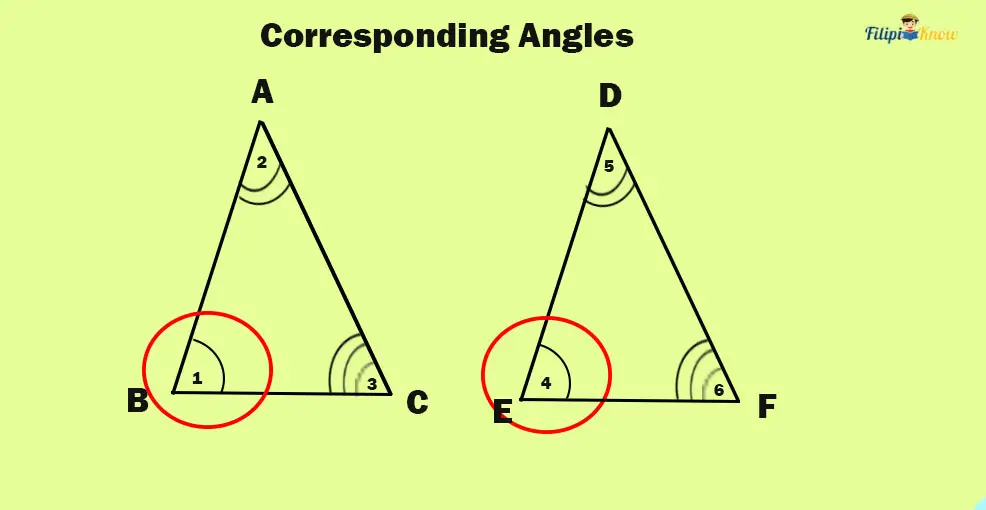
Why do we have to talk about corresponding sides and angles? Well, an important theorem relates congruent triangles to their corresponding parts (the sides and angles). We will discuss this theorem in-depth in the next section.

3. Corresponding Parts of a Triangle are Congruent (CPCTC) Theorem

CPCTC theorem states that if two triangles are congruent, their corresponding parts (sides and angles) are also congruent.

Suppose that triangles ABC and DEF below are congruent triangles:

According to the CPCTC theorem, these triangles’ corresponding sides and angles are also congruent. Thus, side AB is congruent to side DE, side BC is congruent to side EF, and side AC is congruent to side DF. 

Similarly, angle 1 is congruent to angle 4, angle 2 is congruent to angle 5, and angle 3 is congruent to angle 6. 

The tick marks above show which sides and angles are congruent.

Sample Problem: Suppose that triangles PRQ and PTS are congruent. Determine the measurement of angle y.

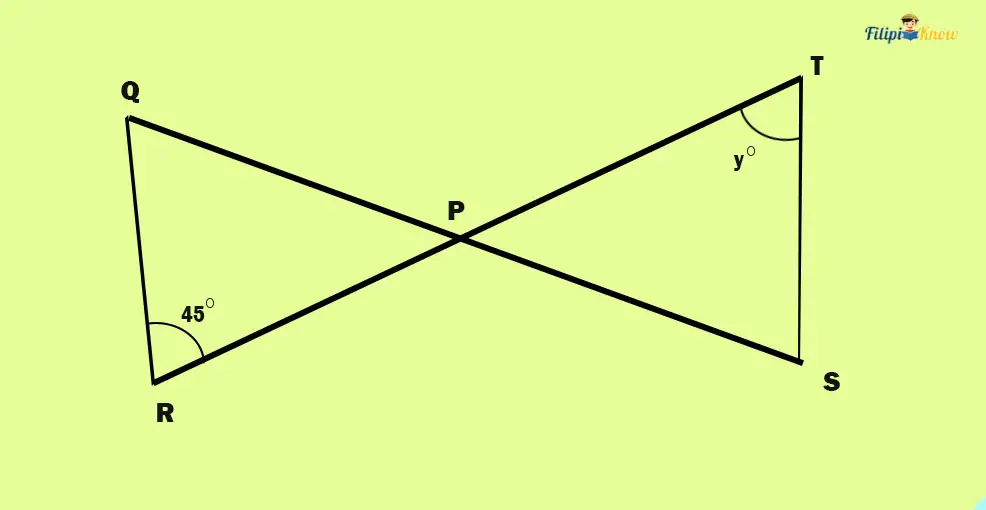
Solution:

Based on the figure above, angle PRQ, which measures 45 degrees, and angle PTS (or angle y) are corresponding angles. Note that triangles PRQ and PTS are congruent. Hence, we can conclude that angles PRQ and PTS are congruent using the CPCTC theorem. Therefore, angle y (or angle PTS) is also 45 degrees.

Triangle Congruence Postulates and Theorems

This section discusses other criteria for determining whether two triangles are congruent. These criteria are some of the geometric postulates that allow us to conclude that two triangles are congruent even without knowing the measurements of every side and angle of the triangles. 

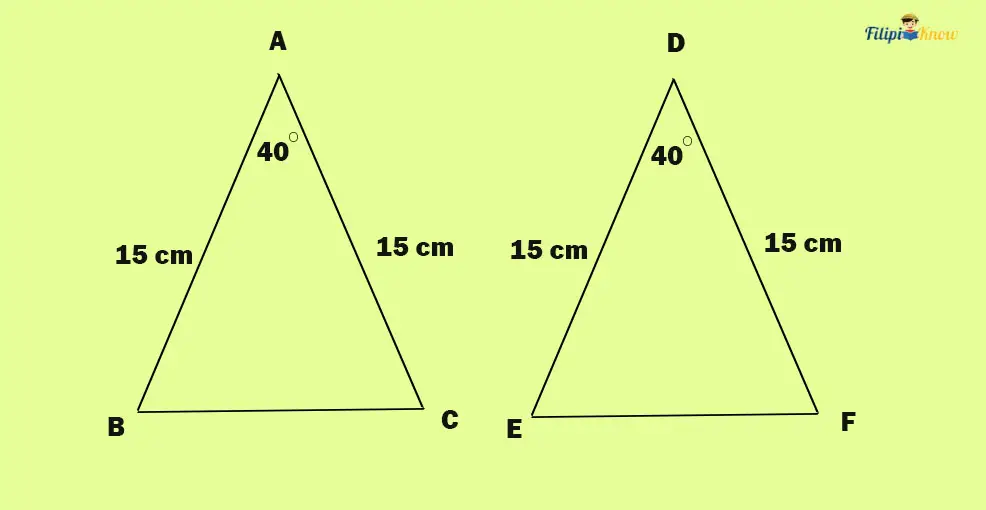
1. Side-Angle-Side (SAS) Postulate

SAS Postulate states that if two corresponding sides and their included angle (the angle located between them) of a triangle are congruent, the triangles are congruent.

In the example below, note that sides AB and DE are congruent (15 cm). Meanwhile, sides AC and DF are also congruent (15 cm). Their included angles are also congruent (both 40 degrees). By SAS Postulate, we can conclude that triangles ABC and DEF are congruent.

2. Angle-Side-Angle (ASA) Postulate

ASA Postulate states that if two corresponding angles and their included side (the side located between them) of a triangle are congruent, the triangles are congruent.

In the figure below, angles LJK and OMN are congruent (40 degrees). Meanwhile, angles JLK and MON are also congruent (60 degrees). Their included sides (JL and MO, respectively) are also congruent (15 cm). As per the ASA postulate, we can conclude that triangles JKL and MNO are congruent. 

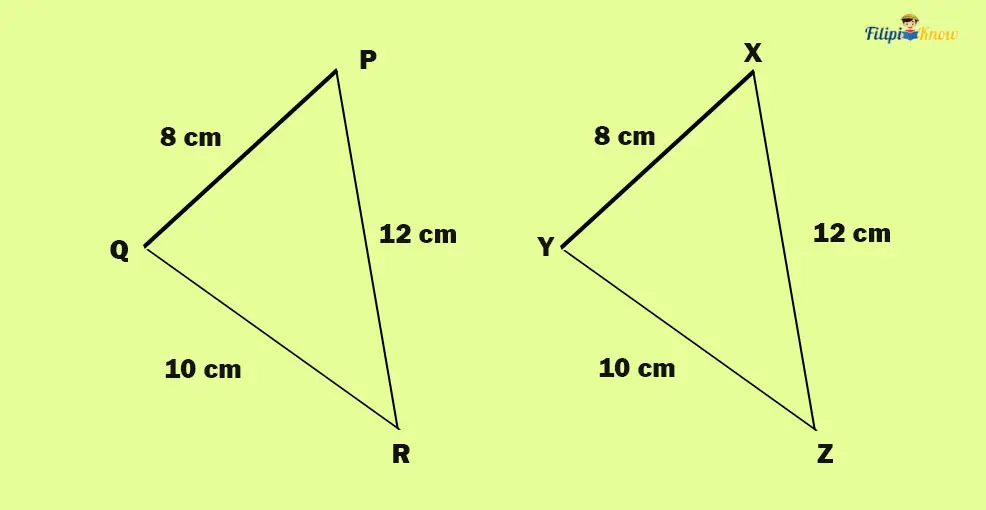
3. Side-Side-Side (SSS) Postulate

The SSS postulate is the most intuitive of the three. It states that if all three sides of two triangles are congruent, they are congruent.

In the figure below, we can conclude using the SSS postulate that the triangles PQR and XYZ are congruent since all of their corresponding sides are congruent. 

More Useful Theorems on Triangles

This section will discuss two useful theorems about triangles that you must learn in geometry.

1. Isosceles Triangle Theorem

“If two sides of a triangle are congruent (i.e., that triangle is an isosceles triangle), then the angles opposite those sides are congruent.”

As we have mentioned earlier, an isosceles triangle is one whose two sides are congruent (the remaining side is not congruent to either).

The isosceles triangle theorem tells us that in an isosceles triangle, the angles opposite to the congruent or equal sides are also congruent. These angles are also called base angles. 

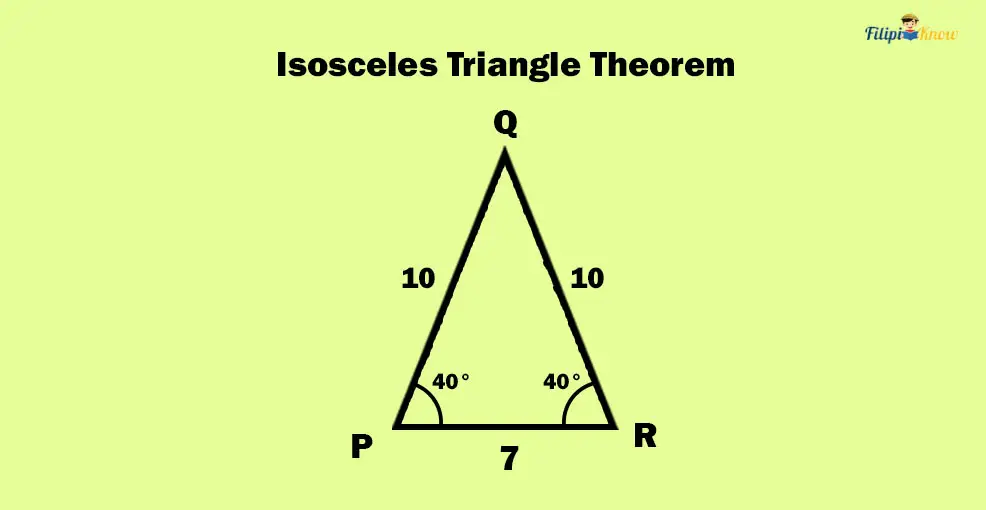
In the figure above, the triangle PQR is isosceles. Side PQ is congruent to side QR. The angles opposite to these congruent sides are angles ∠QPR and ∠PRQ. Per the isosceles triangle theorem, we can state that angles ∠QPR and ∠PRQ are congruent. If m∠QPR = 40°, then m∠PRQ = 40°.

Sample Problem: Using the exact figure above, determine the measure of ∠PQR if m∠QPR and m∠PRQ = 40°

By the isosceles triangle theorem, ∠QPR and ∠PRQ are congruent angles. Hence, m∠QPR = 40°.

Now, how do we find the measure of ∠PQR?

If you remember, the sum of the interior angles of a triangle is always 180°. Therefore, if we add the measurements of angles ∠PQR, ∠QPR, and ∠PRQ, then the sum must be 180°:

m∠PQR + m∠QPR+ m∠PRQ = 180°

We know that both m∠QPR and m∠PRQ are 40°:

m∠PQR + 40 + 40 = 180°

Let us solve for m∠QRP:

m∠PQR + 40° + 40° = 180°

m∠PQR + 80° = 180° Combining like terms

m∠PQR = – 80° + 180° Transposition method

m∠PQR = 100°

Therefore, the measurement of ∠PQR is 100°. 

2. Triangle Inequality Theorem

“The sum of any two sides of a triangle is always greater than or equal to the third side.”

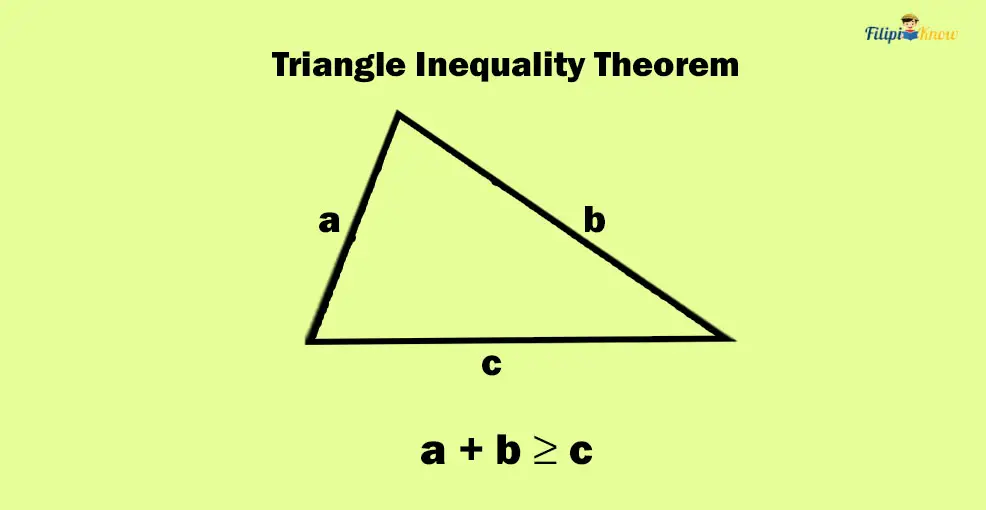
Let us understand this theorem by analyzing the image above. We have assigned variables to the lengths of the triangle’s sides in the figure. The side lengths are a, b, and c.

The triangle inequality theorem states that in any triangle, when you add two sides, the result will always be larger than or equal to the side that you didn’t include in the addition.

Suppose we add sides a and b. By the triangle inequality theorem, a+ b must always be greater than or equal to the side we didn’t include in the addition process (c). Hence, a + b ≥ c.

However, we can add any two sides of the given triangle. For instance, if we add sides a and c instead, the triangle inequality theorem states that a + c must be larger than or equal to b or a + c ≥ b.

Suppose that two sides of a triangle were given, and we want to determine the possible value of the third side. As a consequence of the triangle inequality theorem, the possible length of the third side can be any real number  within this range:

First side – second side < Third side < First side + second side

Don’t fret if you cannot immediately grasp what we are discussing above. Through our examples below, you’ll get a better understanding of the concept mentioned above:

Sample Problem 1: Suppose that two sides of a triangle have measures of 10 cm and 19 cm. Determine the possible measurement of the third side.

Solution: 

We are given two sides of a triangle which are 10 cm and 19 cm. The measurement of the third side is unknown, and we must determine the possible values for its length. 

We cannot just guess the length of the third side since if our guess is too small, the three sides might not form a triangle.  The same applies when our guess is too large; the three sides may not form a triangle. We have to be precise in determining the possible values of the third side to ensure that these three sides will form a triangle.

To find the possible lengths of the third side, we use the following:

   First side – second side < Third side < First side + second side

Our first and second sides are 19 cm and 10 cm, respectively (to avoid negative values):

19 – 10 < third side < 19 + 10

      9 < third side < 29

The result states that the third side’s length can be any real number between 9 and 29 (including 9 and 29). Hence, the possible measurements of the third side can be any number between 9 and 29 inclusively.

This means that if we let the measurement of the third side be any value from 9 to 29, the three sides will form a triangle. For instance, if we let the third side = 15, line segments with 10, 19, and 15 cm measurements will form a triangle. However, if we pick a value outside the range of 9 to 29 (for instance, 8), the sides or line segments will not form a triangle. 

Hence, the possible measurement of the third side is any real number between 9 and 29 inclusively.

Sample Problem: What is the largest possible length of the third side of a triangle if its first and second sides measure 12 cm and 9 cm, respectively?

Solution: 

Using the formula we have used in the previous example:

   First side – second side < Third side < First side + second side

According to the given problem, the first side is 12 cm long, while the second is 9 cm long. By substitution, we have:

12 – 9 < Third Side < 12 + 9

3  < Third Side <  21

Based on our solution above, the length of the third side is the set of all real numbers between 3 and 21 inclusively. Note that the largest value within this set is 21. Since we are looking for the largest possible measurement of the third side of the triangle, the answer is 21 cm.

Next topic: Conversion of Units of Measurement

Previous topic: Angles

Return to the main article: The Ultimate Basic Math Reviewer

Download Printable Summary/Review Notes

Download Printable Flashcards

Test Yourself!

1. Practice Questions [Free PDF Download]

2. Answer Key [Free PDF Download]

3. Math Mock Exam + Answer Key