Clocks, wheels, dining plates, and coins. What do these things have in common?

They are all circular.

We are all familiar with what a circle looks like – it is round, has no sides, and has no start or end. Aside from identifying what it looks like, we also know how important it is to us. As early as the Mesopotamian civilization, people already used circular wheels to do their work and complete their journeys faster.

In this chapter, let us view circles from a “geometric lens” and explore how they’re helpful in our everyday lives. 

Click below to go to the main reviewers:

Ultimate UPCAT Reviewer

Ultimate LET Reviewer

Definition of a Circle

In geometry, we formally define a circle as the set of all points that are equidistant (same distance) from a fixed point. That fixed point is called the center of the circle.

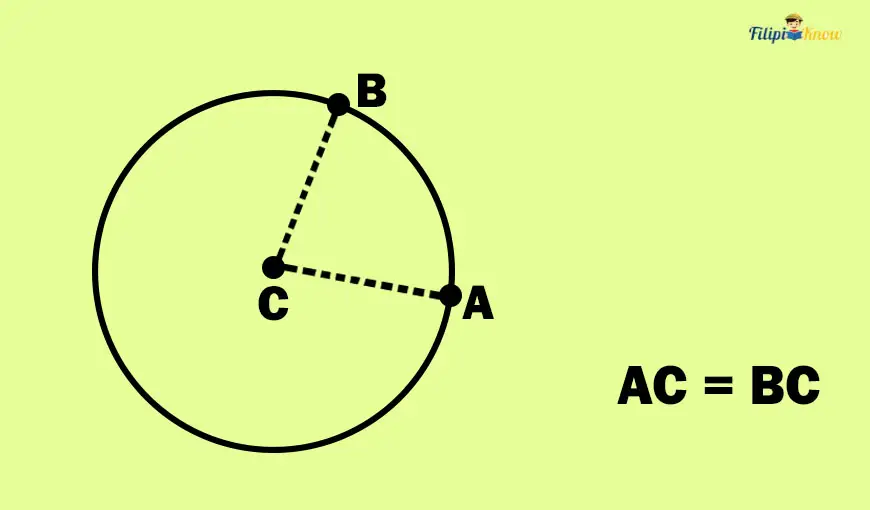
In the image above, point C is the center of the circle. If you take any two points in the circle, you are assured that these points have the same distance from point C. 

Note that when we mention the phrase “on the circle,” it means “in the frame of the circle.”

Suppose that points A and B are both in the circle. The distance from point C to point A is similar to that from point C to point B, or AC = BC.

Now, suppose that you take point D instead; the distance from point C to point D is certainly equal to the distance from point C to A and from point C to point B. Hence, AC = BC = CD.

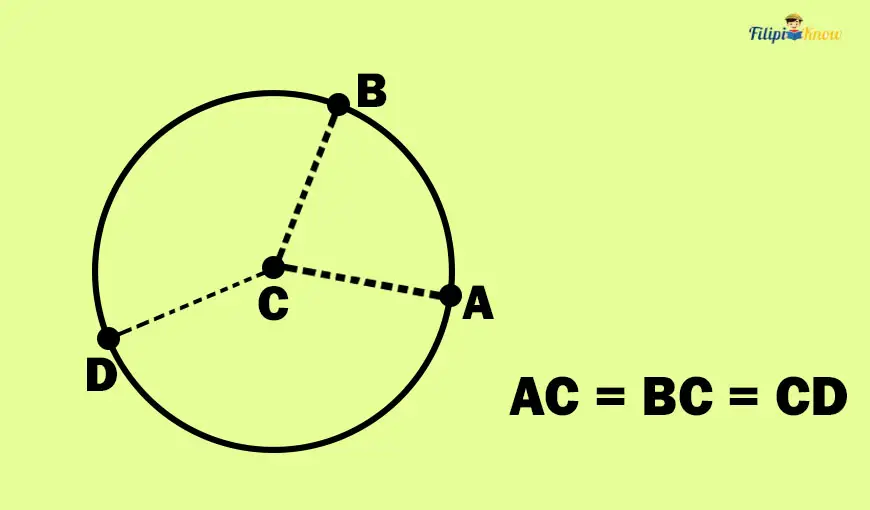
Again, remember that all points on the circle have the same distance from the center.

Radius and Diameter of a Circle

The line segment formed by connecting the center to one of the points on the circle is called the radius.

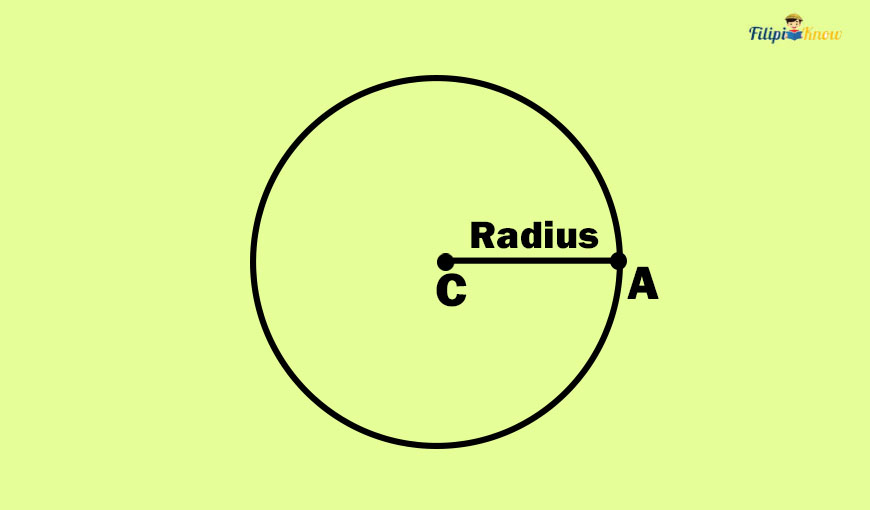
If we draw a line segment from point C to point A in the figure above, we have formed a circle radius, which is segment AC since we have created a segment that connects the center (point C) and a point on the circle (point A).

Since all points on the circle are equidistant (same distance) from the center, all radii (plural of radius) have equal lengths. In other words, all radii are congruent segments. If someone tells you that one of the radii of a circle is longer than the other radius of the same circle, you know that it is false since all radii are equal in length. 

Meanwhile, if you draw a line segment from one point on a circle, pass through the center, and end on another point on the circle, then you have formed a diameter. Segment AQ below is an example of a diameter. The diameter of a circle is a line segment that divides the circle into two equal parts.

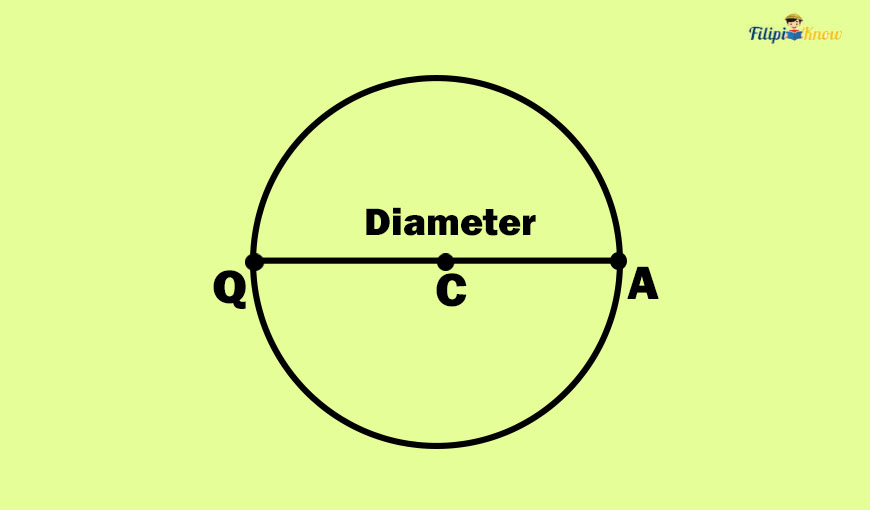
As you have noticed, a diameter consists of two radii (AC and CQ). The length of a circle’s diameter is equal to twice the length of a radius. 

d = 2r (where d is the diameter and r is the radius)

This also implies that the radius of a circle is ½ of the length of the diameter.

Also, like radii, all circle diameters are congruent or have the same length.

Circumference of a Circle

Suppose that you are watching a race in a circular field. How will you know the distance covered by the runners in that field?

The distance covered by the runners is equal to the total distance around the circular field. The total distance around a circle is called the circumference.

The circumference is the counterpart of the perimeter for circles. If squares, triangles, or rectangles have a perimeter as the total distance around them, the circumference is the total distance around a circle.

How do we determine the circumference of a circle?

We use the formula for the circumference of a circle which was derived as early as the ancient Greek civilization:

C = πd

where C represents the circle’s circumference, d is the circle’s diameter, and π is a constant irrational number approximately equal to 3.1416. 

The number π (the Greek letter for “pi,” which is read as “pie”) is one of the most important numbers in mathematics since it’s used extensively not only in geometry but also in trigonometry and calculus. Many mathematicians provided an estimate for this irrational number, but one of the earliest estimations is from the Greek mathematician Archimedes.

π is the result when you try to divide the circumference of any circle on a flat surface by its diameter. It is an irrational number, meaning we cannot express it as a fraction with integers. One of the most common estimations of π used for calculation is 3.14 or 3.1416. However, these estimations are not the actual values of the number since the digits of π are never-ending. One of the most recent estimates of π has 62.8 trillion digits!

Going back to the circumference of a circle, the formula C = πd means that the distance around a circle is equal to the product of the irrational number and the circle’s diameter. Since the diameter of a circle is equivalent to twice the radius of a circle or d = 2r, we can rewrite the formula for the circumference of a circle as: 

C = 2πr

where r is the radius of the circle.

This means that to calculate the circumference of a circle, you can use the following:

• Formula 1: C = πd (if the diameter is given)
• Formula 2: C = 2πr (if the radius is given)

Use formula 1 if the given in the problem is the circle’s diameter. However, if the radius is given, use formula 2.

Sample Problem 1: Determine the circumference of the circle below.

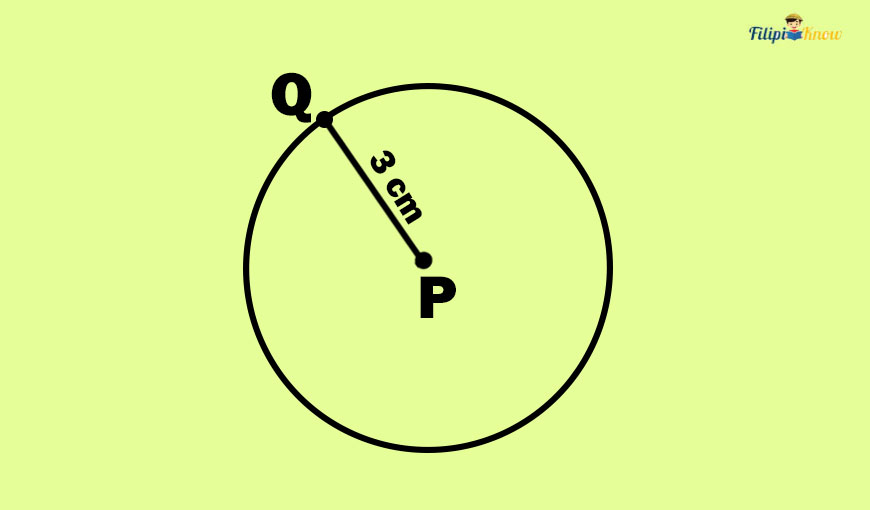
Solution: The circle above has a radius PQ with a length of 3 cm. Since the radius of the circle is given, let us use the formula C = 2πr.

C = 2πr

C = 2π(3) since r = 3

C = 6π

Thus, the circumference of the circle is 6π cm.

Sometimes, the problem provides us with an estimated value of π that we should use in the problem. For instance, look at the given problems below.

Sample Problem 2: Compute the circumference of the circle below. Use π = 3.14.

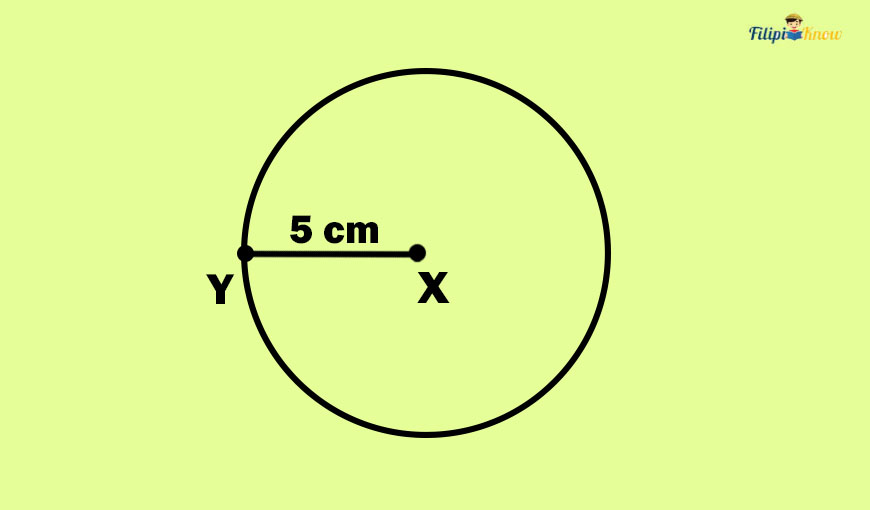
Solution: The circle above has a radius of XY with a length of 5 cm. Since the radius of the circle is given, let’s use the formula C = 2πr.

C = 2πr

C = 2(3.14)(5) Take note that the problem provides the value of π

C = 31.4

Hence, the circumference of the circle is 31.4 cm.

Sample Problem 3: Calculate the circumference of a wheel with a diameter of 20 centimeters. Use π = 3.14.

Solution: We are given the diameter of the wheel. Thus, it is more convenient to use the formula C = πd.

C = πd

C = (3.14)(20)

C = 62.8

Hence, the circumference of the circle is 62.8 cm.

Sample Problem 4: The rim of a basketball ring has a circumference of 56 inches. Determine the diameter of the basketball ring.

Solution: The problem states that the rim of the basketball ring has a computed circumference of 56 inches. 

Recall that the circumference of a circle can be calculated using the formula:

C = πd

We will use this formula instead of the other one since we are looking for the diameter of the ring.

The circumference is 56 inches. So, we have C = 56: 

56 = πd

The problem doesn’t provide a precise estimate of π, so we leave it as it is.

Let us now solve for the diameter (d) by dividing both sides by π:

56 = πd

πd = 56 Symmetric Property of Equality

πd⁄π = 56⁄π Dividing both sides of the equation by π

d = 56⁄π

Thus, the diameter of the basketball ring is 56⁄π inches.

Sample Problem 5: The motorcycle’s wheel has a radius of 30 cm. How many revolutions must the wheel make to cover a total distance of 18.84 meters (1,884 centimeters)? Use π = 3.14.

Solution: When a wheel makes one revolution, it revolves at a total distance equivalent to its circumference. In other words, one revolution of the wheel = circumference of the circle.

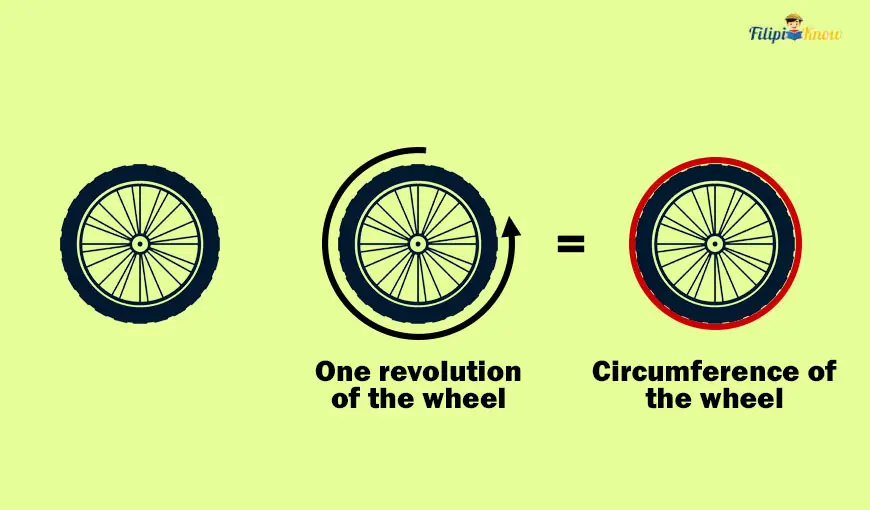
Therefore, to find the number of revolutions it takes for the wheel to cover a total distance of 1,884 centimeters, we must divide 1,884 by the wheel’s circumference.

Let us first compute the circumference of the wheel.

The problem states that the wheel has a radius of 30 cm. Thus, we need to use the formula C = 2πr. Note that the problem requires us to use π = 3.14.

C =  2πr

C = 2(3.14)(30) Substitute r = 30 and π = 3.14

C = 188.4

Hence, the circumference of the wheel is 188.4 centimeters.

Now, to determine the number of revolutions the wheel will make to cover a total distance of 1,884 centimeters, let us divide 1,884 by the wheel’s circumference (188.4).

Number of revolutions = 1,884 ÷ 188.4 = 10

Thus, the answer to this problem is 10 revolutions.

Area of a Circle

The area of a circle refers to the amount of space a circle occupies on a flat surface. 

To calculate the area of a circle, we use the formula below.

A_circle  = πr²

where r is the circle’s radius, and π is the constant irrational number approximately equal to 3.1416.

The formula above states that the area of a circle is the product of the square of a circle’s radius and π.

How does the circumference differ from the area of a circle? Take a look at the image below.

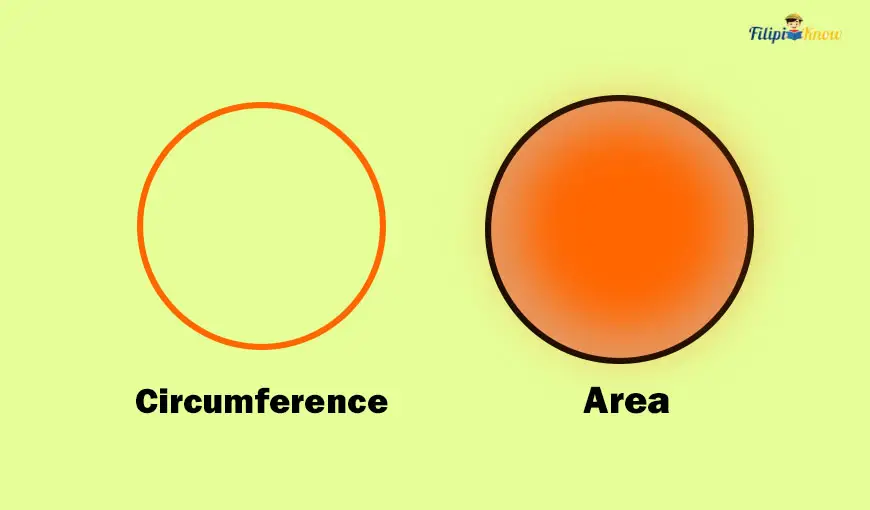
The circumference is the total distance around a circle. It measures how long the boundary of that circle is. Meanwhile, the area measures how much space is occupied inside the circle.

Recall that when providing the area of a plane figure, we write the units in square unit form. For instance, if the circle’s radius is given in centimeters (cm), its area must be in square centimeters (cm²). Similarly, if the unit of measurement is given in inches (in), then the area must be written in square inches (in²). Take note of this reminder because even if your calculation is correct, but your unit is not, your final answer will be considered incorrect.

Sample Problem 1: A circle has a radius of 2 meters. Determine its area.

Solution: We only have to use the formula for the area of a circle to solve the problem. Furthermore, take note that the problem doesn’t provide an estimate of π. Thus, we use π as it is.

A_circle = πr²

A_circle = π(2)² Substitute r = 2

A_circle = 4π

Thus, the area of the circle is 4π m².

Sample Problem 2: The radius of a circle is ½ inches long. Determine its area (Use π = 3.14).

Solution: Let’s use the formula for the area of a circle for this problem.

Please take note that we have r = ½ for this problem. However, converting ½ into a decimal form is much easier, so all of our figures in the formula will be decimal numbers. If you convert ½ into decimal form, you will get 0.5.

A_circle = πr²

A_circle = (3.14)(0.5)² Substitute r = 0.5

A_circle = (3.14)(0.25)

A_circle = 0.785

Therefore, the area of the circle is 0.785 square inches.

Sample Problem 3: Determine the area of the circle below (Use π = 3.14):

Solution: The image above provides us with the circle’s diameter of 10 cm. We cannot use the diameter to compute the area of the circle since the formula requires us to have the circle’s radius and not the diameter.

Recall that the diameter is equivalent to twice the radius of the circle. Hence, if the circle above has a diameter of 10 cm, then its radius is 10⁄2 = 5 cm.

Now that we have r = 5 cm. Let us compute the area of the circle using the formula:

A_circle = πr²

A_circle = (3.14)(5)² Substitute r = 5

A_circle = (3.14)(25)

A_circle = 78.5 

Thus, the area of the circle above is 78.5 cm².

Sample Problem 4: The inscribed square (square inside the circle) in the image below has a perimeter of 24 cm. Meanwhile, the circle has a radius of 10 cm. Determine the area of the shaded region in the image below.

Solution: The problem above takes a little bit of analysis. How will you find the shaded region’s area in the image above?

If you try to remove the inscribed square in the image, you might notice that the remaining figure will be the shaded region. Hence, the area of the shaded region can be calculated if we are going to subtract the area of the square from the area of the circle:

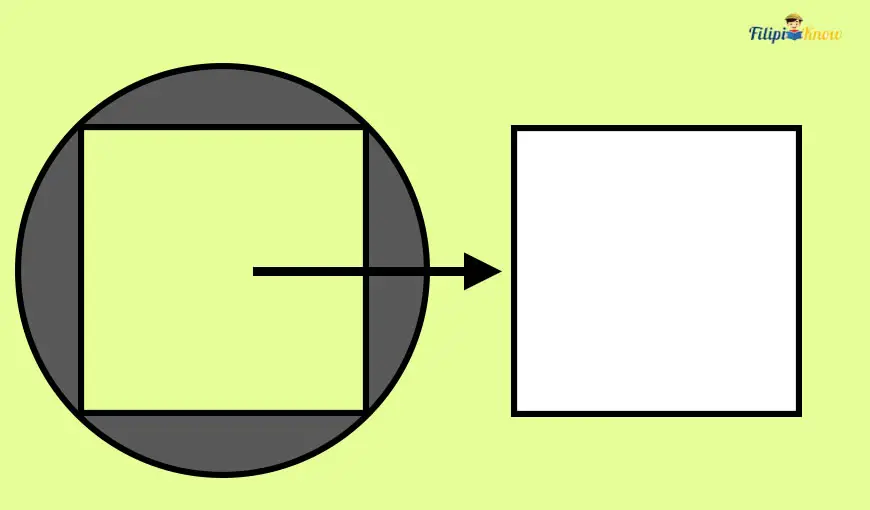
A_{shaded region}  = A_circle  – A_square

So, to find the area of the shaded region, we must first find the areas of the square and the circle.

Let us compute the area of the square first.

The problem states that the perimeter of the square is 24 cm. Recall that a square’s perimeter equals four times its side or P = 4s. Thus, if 24 is the perimeter of the square, then its side is:

24  = 4s

24⁄4  = 4s⁄4 Dividing both sides of the equation by 4

6 = s

s = 6

Thus, the side of the square in the figure is 6 cm. We can now calculate the area of the square.

Recall the formula for the area of the square: A_square = s²

A_square = s²

A_square = (6)² Since s = 6

A_square = 36

Therefore the area of the square is 36 cm².

Let us now compute the area of the circle.

The radius of the circle is 10 cm. Thus, we have r = 10. Let us use the formula for the area of a circle. Note that the problem does not provide us with an estimation of π that we should use, so we use π as it is.

A_circle  = πr²

A_circle = π(10)²

A_circle = 100π

Hence, the area of the circle is 100π cm².

We are not done yet. Remember that we are looking for the area of the shaded region. We have stated earlier that the area of the shaded region is equivalent to the difference between the area of the circle and the area of the square:

A_{shaded region}  = A_circle – A_square

A_{shaded region} = 100π – 36

That’s it! The area of the shaded region is 100π – 36 cm².

Let us now move on to other concepts related to circles, such as the arcs and angles of a circle.

Arcs of a Circle

An arc is a portion of the circumference of a circle. It is formed by two points that are on the circle.

In the image above, the red-colored part of the circumference of a circle is an example of an arc. Points X and Y, which are on the circle, are the endpoints of this arc. We call this arc XY. In symbols:

Measurement of an Arc

The measurement of an arc refers to the measure of the central angle of the circle that intercepts that arc. 

Let us go back to the previous example. You can create an angle that intercepts (or touches) the arc with the circle’s center as the vertex. That angle is called a central angle. 

In the figure above, we draw ∠XCY with C as the vertex. This is a central angle since its vertex is the circle’s center. Now, notice that this central angle intercepts or touches the arc XY.

The degree measurement of the central angle that touches the arc is the degree measurement also of that arc. Hence, in the figure above, if m∠XCY = 30°, then the measurement of the arc that it intercepts is also 30°.

Just like angles, we use degrees (°) as a unit of measurement for arcs.

The measurement of an arc can be any real number from 0° to 360°. The whole circle (the entire circumference) measures 360°.

We will discuss more central angles in the latter part of this review module, but in the meantime, this intuitive meaning of the measurement of an arc should be enough for you to continue to the next section.

Types of Arcs

We can classify arcs according to the degree measurement: minor arcs, semicircles, or major arcs.

1. Minor Arc

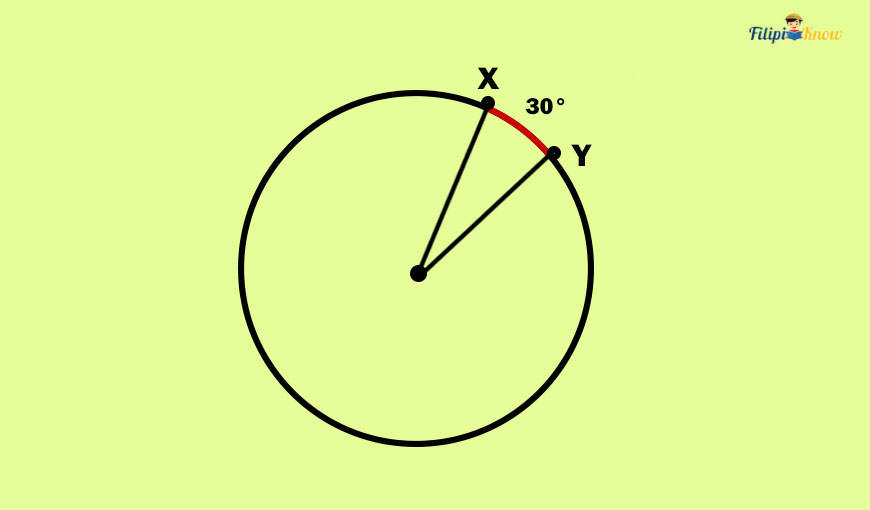
A minor arc is an arc with a measure that is less than 180°.  

Arc XY is an example of a minor arc since its degree measurement is only 30°, less than 180°.

2. Semicircle

A semicircle is an arc with a measure that is exactly 180°.

In the image above, arc PQ is a semicircle since it has a degree measurement of 180°. 

You might also realize that the semicircle is half of the circle. Thus, we can state that the distance of the arc created by a semicircle is equal to ½ of the circumference of the circle. Moreover, all circles have two semicircles.

3. Major Arc

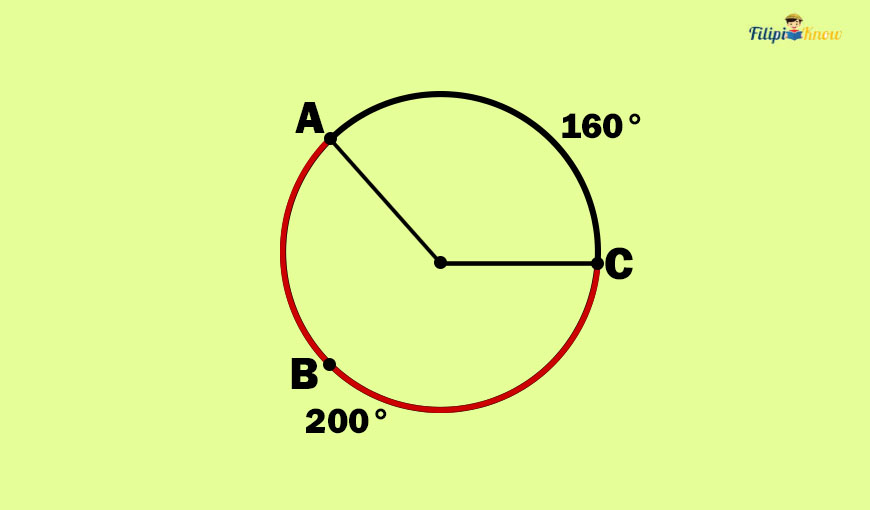
A major arc has a degree measurement greater than 180° but less than 360°.

To name a major arc, we use three letters: two letters for the arc’s endpoints, and the third one is the point between these endpoints.

Arc ABC is a major arc since it has a measurement of 200°. 

The measurement of a major arc is equivalent also to 360 minus the measurement of the minor arc with the same endpoints as the major arc. 

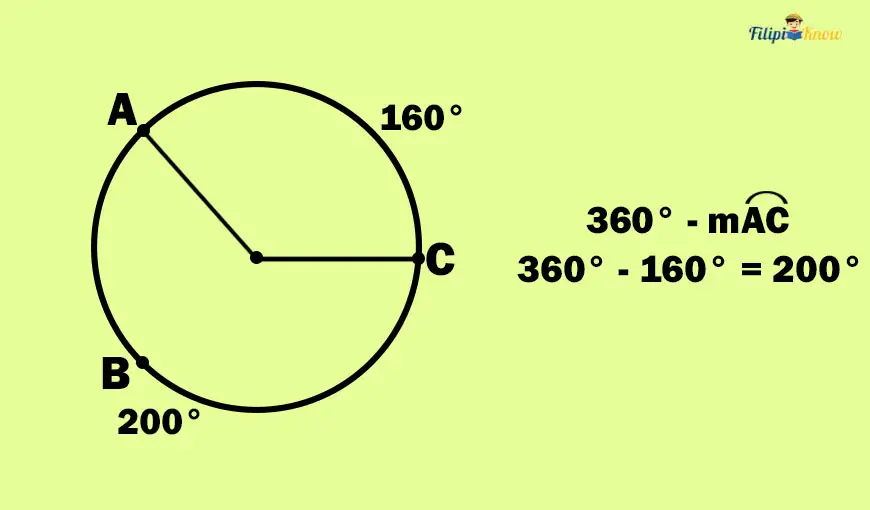
For instance, if arc AC is 160°, we can compute the measurement of arc ABC by subtracting the 160° from 360°. Thus, the measurement of arc ABC is 200°.

Arc Addition Postulate

If an arc is formed by two adjacent arcs, then the measurement of the arc that is formed is equivalent to the sum of measurements of the adjacent arcs.

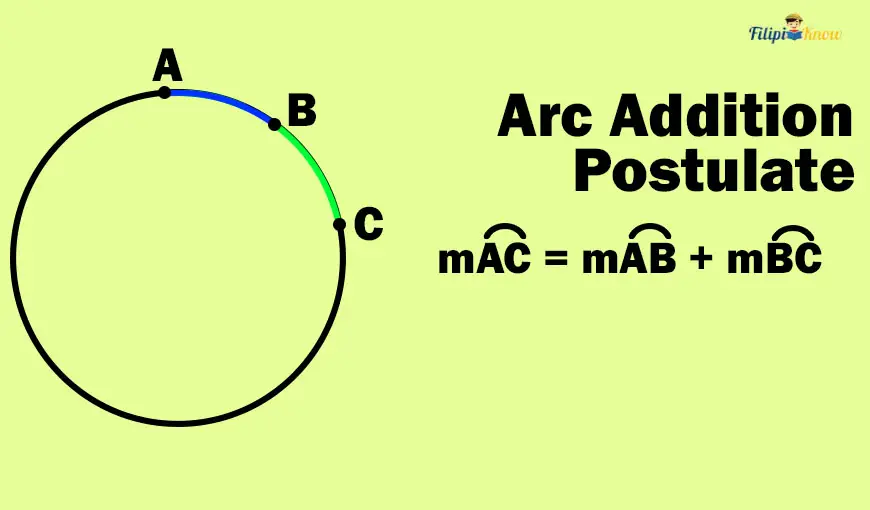
The arc addition postulate is analogous to the angle and segment addition postulates. 

In the figure above, arc AC is formed by adjacent arcs AB and BC. The arc addition postulate tells us that

 m= m+ m

Sample Problem: Determine the measure of if m = 42° and m= 72°.

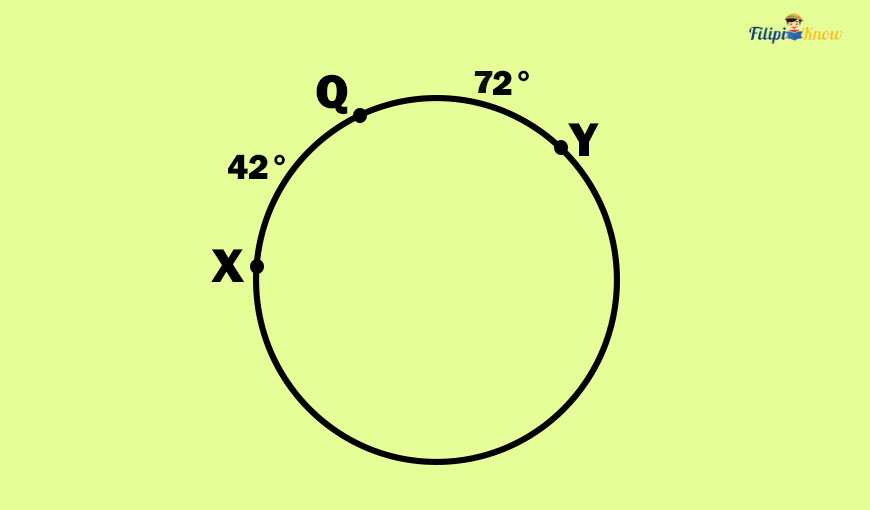
Solution: By the arc addition postulate,

m=   m + m 

m=  42° + 72° 

m=  114°

Chords, Secants, and Tangents of a Circle

This section discusses other circle parts, such as chords, secants, and tangents.

A chord is a segment with endpoints that are points on a circle. A secant is a line that intersects a circle in two points. Meanwhile, a tangent is a line intersecting a circle at exactly one point. 

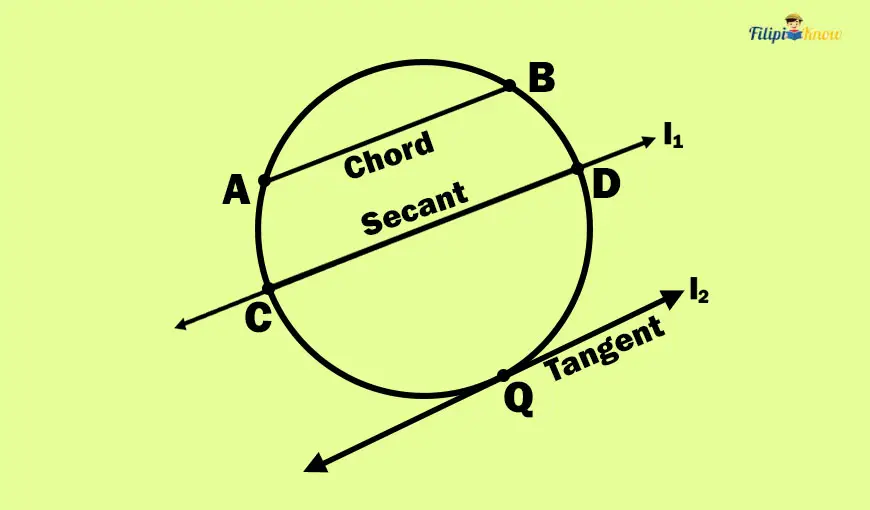
In the figure above, segment AB is a chord since its endpoints are points on the circle (A and B). Meanwhile, Line l₁ is a secant since it is a line that intersects the circle at two points (which are C and D). Lastly, Line l_₂ is a tangent since it is a line that intersects the circle at exactly one point (which is at point Q). The point where the tangent and the circle intersect is called the point of tangency (Q is a point of tangency).

Also, note that the diameter is also a chord of a circle.

Some Theorems on Chords, Secants, and Tangents

Here are some important theorems that you must know about these three features of a circle:

1. Theorem: In a circle, two minor arcs are congruent if and only if their corresponding chords are congruent.

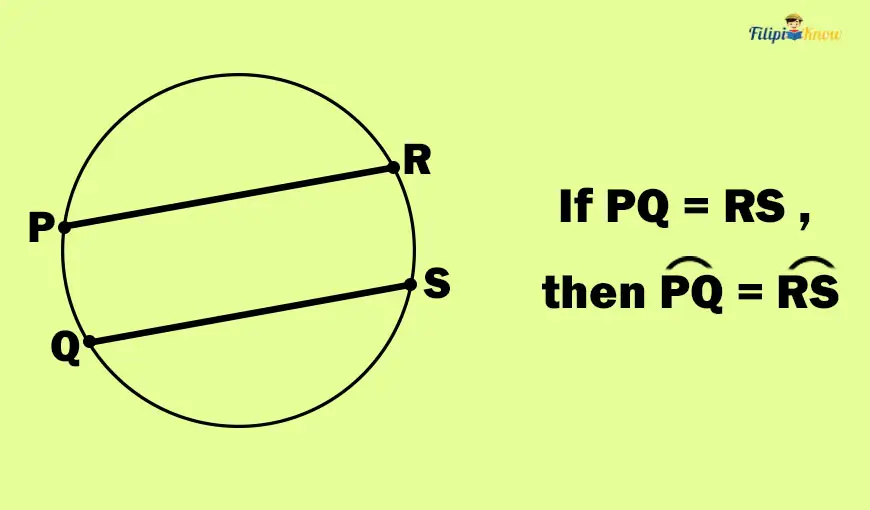
To better explain the theorem above, look at the given figure above.

PR and QS are congruent chords. This means that these chords have equal measurements or lengths. Since these chords are congruent, the theorem above tells us that their corresponding arcs, arc PQ and arc RS, are also congruent. 

So, in the figure above, if m = 55°, then m = 55° also.

2. Theorem: Tangent segments from a common external point are congruent.

In the figure above, line segments JK and JL have a common external point of J. As per the theorem above, since both of these segments are tangent to the circle (this means that each intersects the circle at exactly one point only), JK and JL are congruent or have equal lengths.

So suppose JK = 15 cm, then JL must be 15 cm since JK and JL are congruent according to the above theorem. 

3. Theorem (Segment of Chords Theorem): If two chords of a circle intersect, then the product of the segments of the first chord is equal to the product of the segments of the second chord.

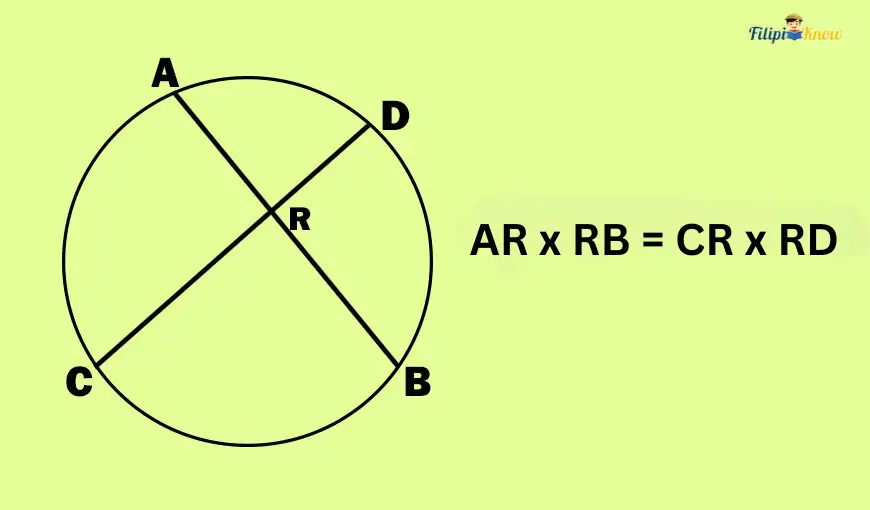
To understand this theorem better, please refer to the image above. 

Chords AB and CD intersect at point R. The theorem tells us that the product of AB (AR and RB) segments is equal to the product of CD (CR and RD). In symbols: AR x RB = CR x RD.

Sample Problem 1: Find the value of x in the figure below.

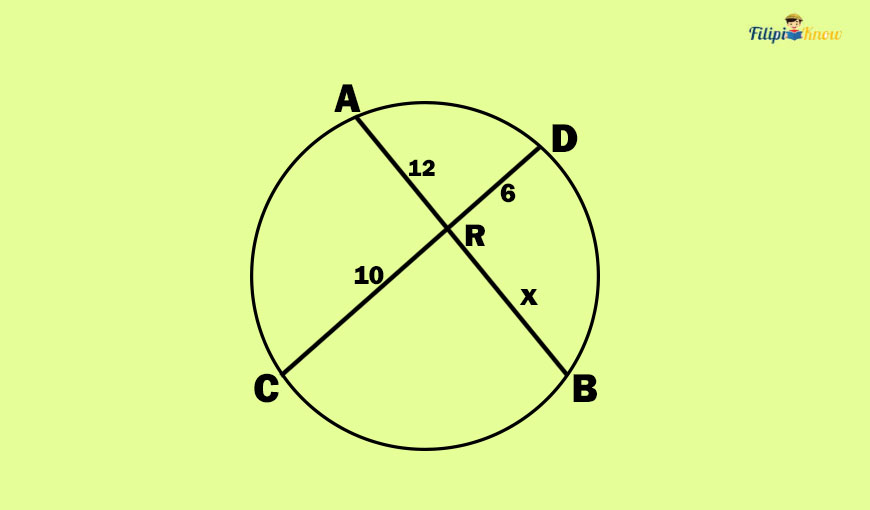
Solution: In the figure above, x indicates the RB (or BR) measurement, a chord AB segment.

The Segment of Chords Theorem tells us that AR x RB = CR x RD (we have discussed this above). 

Let us use this theorem to find x:

AR ⋅ RB = CR ⋅ RD Replace the “x” sign with”⋅” since we are using x as a variable

12 ⋅ x = 10 ⋅ 6 Substituting the given values in the problem

12x = 60 Simplifying the equation

12x⁄12 = 60⁄12 Dividing both sides of the equation by 12

x = 5

Hence, the value of x is 5. 

4. Theorem (Segment of Secants Theorem): If two secant segments have a common external endpoint, then the product of the lengths of the entire secant segment and its external segment is equal to the product of the lengths of the other entire secant segment and its external segment.

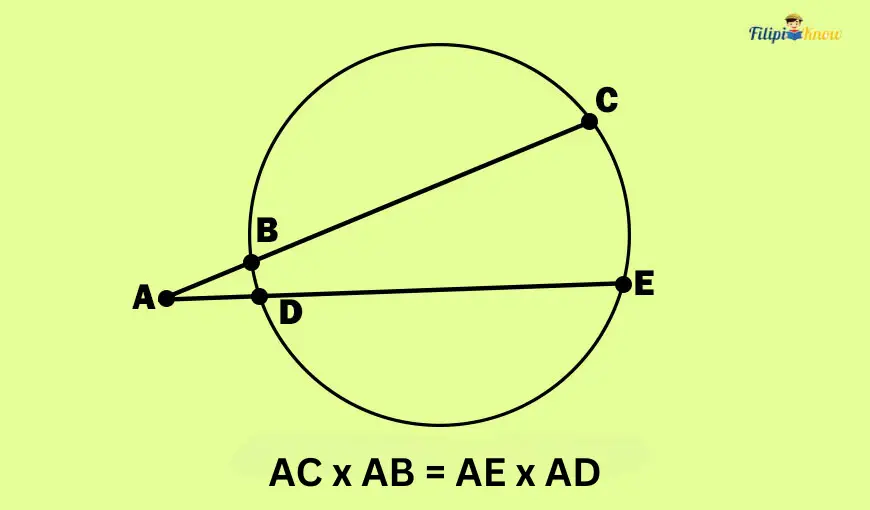
Let us take a look at the image above. Segments AC and AE are secant segments since both intersect two points of the circle. Furthermore, these segments share a common external endpoint which is A. Hence, the theorem above applies to these secant segments.

The theorem states that if we multiply the length of the entire secant segment AC by its external segment, which is AB (it is external since AB is outside the circle), then the result will be equal to the result when we multiply the entire segment AE by its external segment AD. 

In symbols: 

AC (entire secant segment) ⋅ AB(external segment of AC) = AE(entire secant segment) ⋅ AD (external segment of AE)

Sample Problem: Determine how long the segment PU is in the image below.

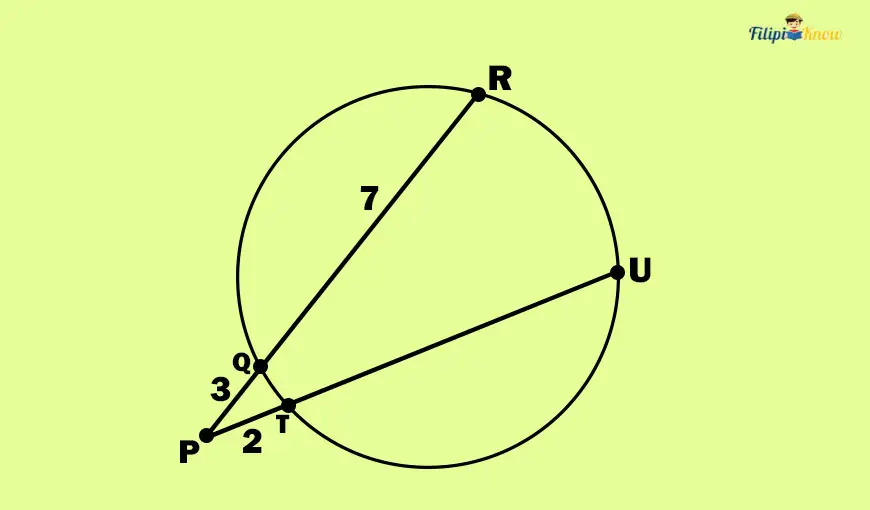
If you look carefully at the image above, PR and PU are secant segments that share a common external endpoint which is P. Thus, we can apply the Segment of Secants Theorem to find the length of segment PU. 

The Segment of the Secants Theorem allows us to conclude that the product of the entire secant segment PR and its external segment (which is PQ) is equal to the product of the entire secant segment PU and its external segment (which is PT).

Thus, we can write this equation:

PR ⋅ PQ = PU ⋅ PT

Let x be the length of segment PU:

PR ⋅ PQ = x ⋅ PT

Note that the segment PR is ten units long (since PR = PQ + QR by the segment addition postulate). 

Using the given values in the image above:

10 ⋅ 3  = x ⋅ 2

Simplifying the equation above:

30 = 2x

By the symmetric property of equality

2x = 30

If we divide both sides of the equation by 2, we will obtain the following:

2x⁄2 = 30⁄2

x = 15

Since x represents the length of the secant segment PU, then PU = 15 units.

Central Angles and Inscribed Angles

Angles can also be observed in a circle and have interesting properties you must know.

1. Central Angle

You have already encountered central angles in our earlier discussion about measuring an arc of a circle. Again, a central angle is an angle such that its vertex is the center of a circle, and its sides are the circle’s radii.

In the figure below, ABC is a central angle since its vertex is the circle’s center, B, and its sides are radii of the circle (AB and AC).

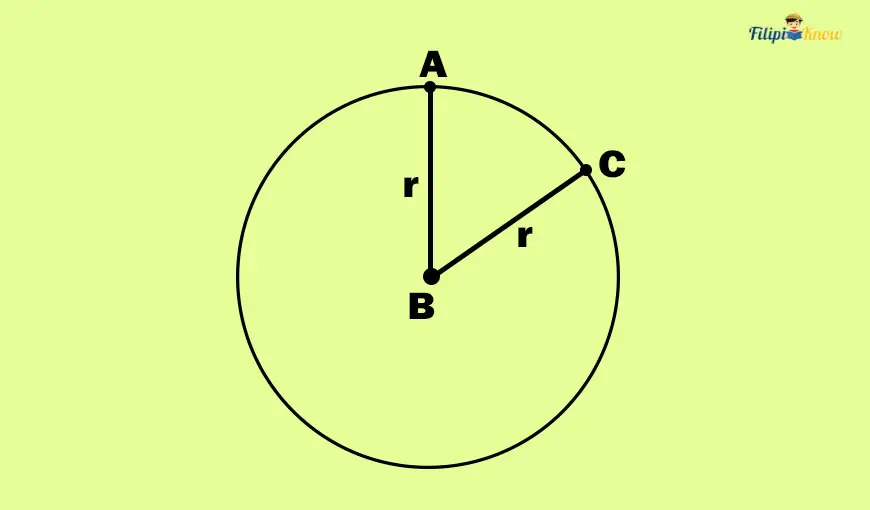
To reiterate what you have also learned earlier, the central angle and its intercepted arc have the same measurement. In other words, the central angle and its intercepted arc have the same measurement. Thus, in the figure above, ABC is congruent with its intercepted arc AC.

Sample Problem: Solve for the value of x below.

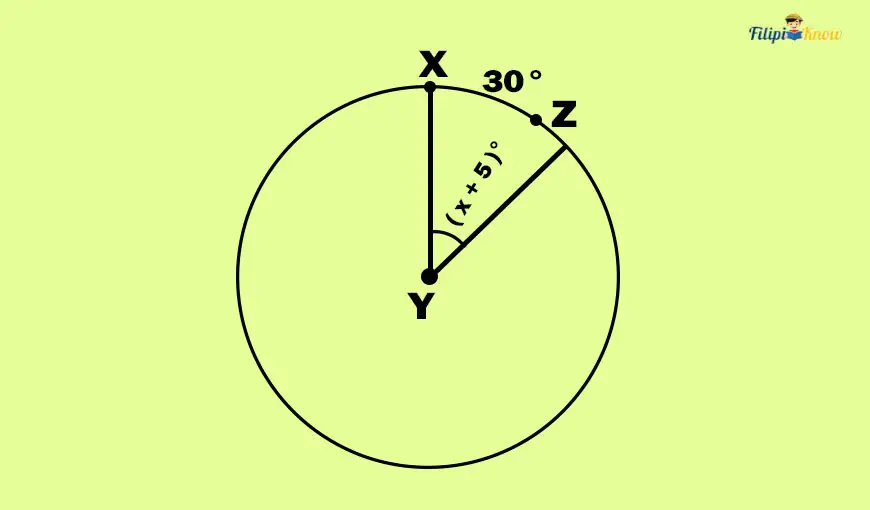
In the figure above, angle XYZ is a central angle that intercepts the arc XZ. We know that the measurement of the central angle is equal to its intercepted arc, thus:

m∠XYZ = m

Using the given values in the image above:

x  + 5 = 30

We can now solve for x by simply transposing 5 to the right-hand side of the equation:

x  + 5 = 30

x  = -5 + 30

x = 25

Thus, the value of x is 25.

2. Inscribed Angle

If the vertex of an angle is a point on the circle and its sides contain chords of the circle, then that angle is inscribed.

In the image above, FOR is an inscribed angle since its vertex is F, a point on the circle, and its sides, ray FO and FR, contain chords of the circles.

Inscribed Angle Theorem: “The measurement of an inscribed angle is equal to ½ of the measurement of its intercepted arc.”

The inscribed angle theorem provides us with a way to determine the measurement of an inscribed angle given its intercepted arc (or the arc it touches). According to the theorem, the measurement of an inscribed angle is just half of the measurement of its intercepted arc.

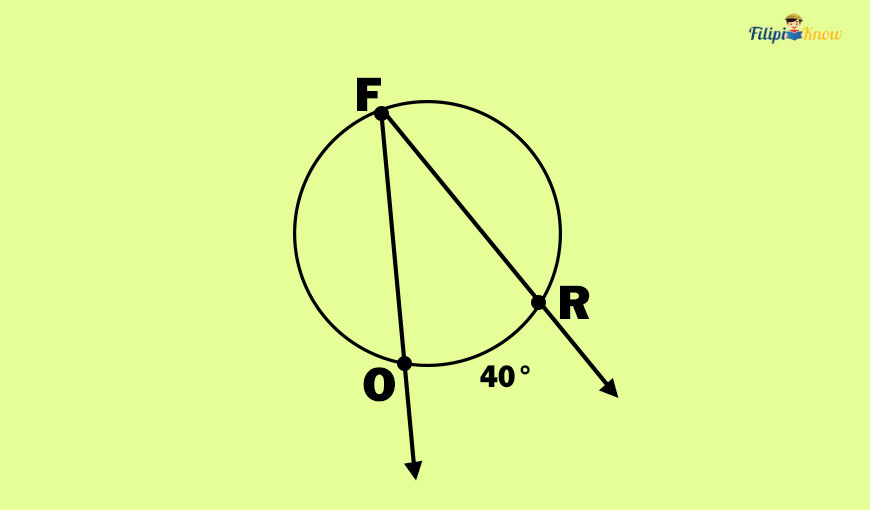
In the figure above, is 40°. is the intercepted arc of FOR. Thus, the measurement of ∠FOR is half the measurement of   which is 40⁄2 = 20°.

Thus, m∠FOR = 20°.

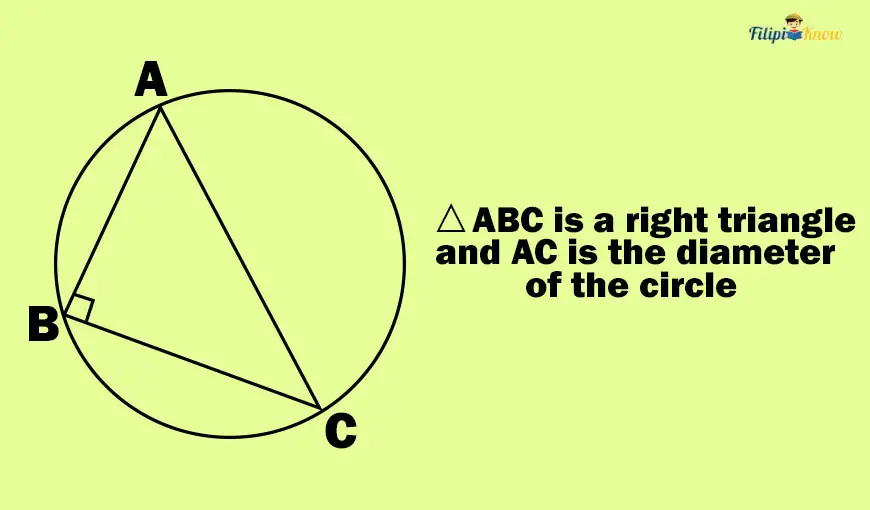
Using the inscribed angle theorem, can you prove that the angle will be right when you inscribe an angle in a semicircle?

Recall that a semicircle has a degree measurement of 180°. Thus, if you inscribe an angle in it, its measure will be half of the measurement of the semicircle. Half of 180° is 90°. Therefore, the inscribed angle is a right angle.

Hence, if an angle is inscribed in a semicircle, that angle is a right angle.

Inscribed Polygon

An inscribed polygon is one in which all vertices lie on a circle. Meanwhile, the circle that contains that polygon and touches its vertices is called a circumscribed circle.

In the image below, the trapezoid is an inscribed polygon, while the circle that contains it is a circumscribed circle.

If you inscribe a right triangle in a circle, the longest side of the right triangle (called the “hypotenuse”) will be the diameter of that circle. 

Next topic: Right Triangles

Previous topic: Volume of Solid Figures

Return to the main article: The Ultimate Basic Math Reviewer

Download Printable Summary/Review Notes

Download Printable Flashcards

Test Yourself!

1. Practice Questions [Free PDF Download]

2. Answer Key [Free PDF Download]

3. Math Mock Exam + Answer Key