In 1665, Isaac Newton invented calculus, a branch of mathematics that has changed the way we understand the world around us. 

As a brilliant mathematician and physicist, he used calculus’s rigors to explain some physics laws. From thereon, the applications of calculus have transcended physics and become useful in various fields such as chemistry, biology, engineering, statistics, economics, computer science, business analysis, and a lot more.

In this module, we’ll begin our calculus study by learning the concept of limits.

Click below to go to the main reviewers:

Ultimate LET Reviewer

Ultimate UPCAT Reviewer

An Introduction to Limits

Consider the function below

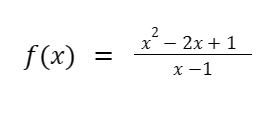
Recall that we can use any real number as the input value of x for this function and be assured that the output we will get is a real number, except when we substitute x = 1.

But why?

If we let x = 1 and input it in the function above, we will obtain a denominator of 0, which is not defined in the set of real numbers. Recall that division by 0 is undefined.

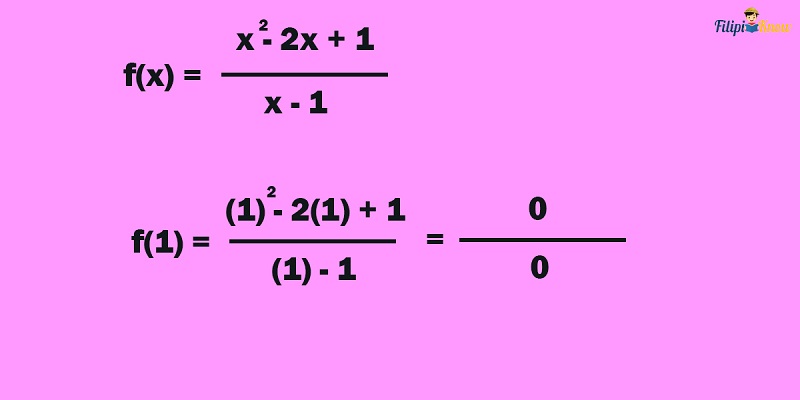
What will happen if we substitute values of x that are very near or approaching 1 instead? For instance, let us try substituting the values x₁ = 1.1, x₂ = 1.09, x₃ = 1.05, x₄ = 1.02, and x₅ = 1.01. Note that these x values are extremely near, or we can say “approaching the value of x = 1”. Also, note that these values are on the right of 1.

x	f(x)
1.1	0.1
1.09	0.09
1.05	0.05
1.02	0.02
1.01	0.01
1.001	0.001
1.0001	0.0001

Note that as the value of x gets closer and closer to the value of 1 from the right, the value of f(x) becomes closer to 0. This means that if we insert the values of x that are incredibly close to 1 from the right of it, the value of f(x) tends to approach 0. 

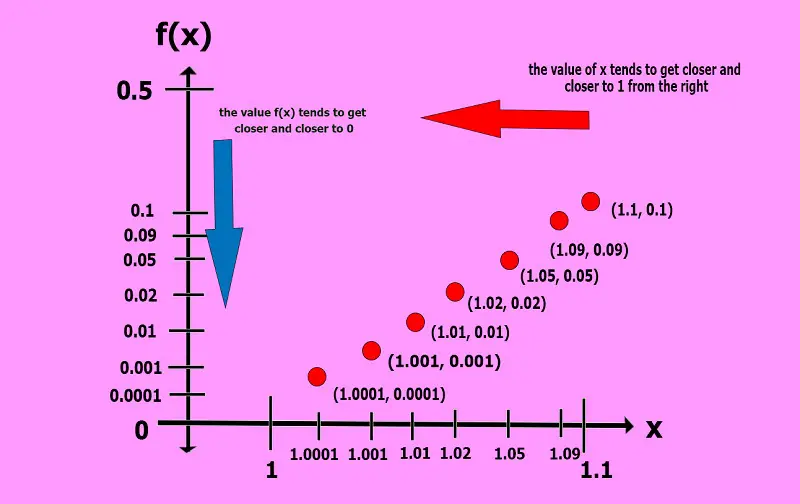
In symbols, x → 1, f(x) → 0 (“as the value of x approaches 1, the value of f(x) approaches 0”).

Now, let us consider values extremely close to 1 from the left such as x₁ = 0.9, x₂ = 0.99, x₃ = 0.999, x₄ = 0.9999, and x₅ = 0.99999. Again, these values are on the left of 1 and are extremely close to it.

x	f(x)
0.9	-0.1
0.99	-0.01
0.999	-0.001
0.9999	-0.0001
0.99999	-0.00001

As you can see, the closer the values of x to 1 from the left, the closer the f(x) value to 0. We also see this behavior when considering values close to 1 from the right. This means that in either direction (right or left), as the value of x becomes closer to 1, the value of f(x) tends to approach 0.

This means that the limit of the sample function above as x approaches 1 is 0.

Note that based on our analysis above, substituting x = 1 to the function doesn’t mean that the resulting value of f(x) is 0; it only means that the behavior of the function tends to reach 0 as we substitute values of x that are incredibly close to 1 from the left or the right of it.

From our example above, we can state the intuitive definition of limits.

Intuitive Definition of Limits

“Given that f(x) is a function and a is a real number, if the values of f(x) approach the real number value of L as the values of x approach or get closer and closer to a, then the limit of f(x) as x approaches a is the real number L.”

Let’s go back to our example: 

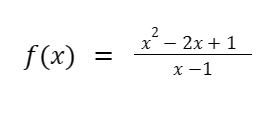
The limit of the function is 0 as x approaches 1. This is because when substitute values of x get extremely close to 1, whether less than (on the left of) or greater than (on the right of) 1, the value of f(x) approaches 0. 

It is important to note that even if the limit of f(x) is 0 as x approaches 1, it doesn’t mean that f(1) = 0 or the value of f(x) is 0 when we let x = 1. Again, the f(x) value would still be undefined at x = 1. The limit of 0 only tells us that the function’s behavior tends to reach 0 as we substitute values of x that are very close to 1.

Again, note that the definition above is just an intuitive approach to defining a limit. The formal definition of it, known as the “Epsilon-delta definition for limits,” is taught in higher mathematics classes, so we will not cover it in this review. 

Notation for Limits

We use a shorthand notation to express the limit of a function concisely. If the limit of the function f(x) is a real number L as x approaches a, then we can write it as:

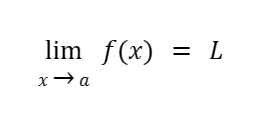
The notation reads, “The limit of f(x) as x approaches a is L.”

Going back to our earlier example,

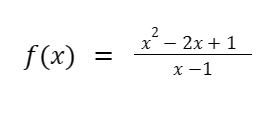
If the limit of the function above is 0 as x approaches 1, then we can express it in this notation:

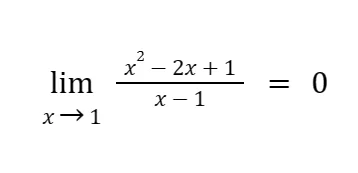
Sample Problem: Express the following using the shorthand notation for limits

1. The limit of x + 3 as x approaches 3 is 6

2. The limit of

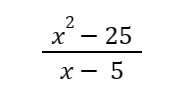
as x approaches 5 is 10

Solution:

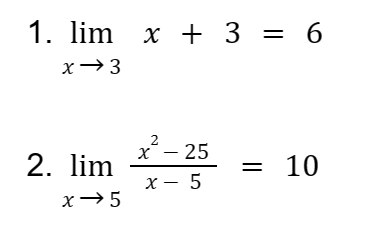
Non-Existent Limits

Consider the function below.

If we try substituting x = 0 for this function, we will obtain an undefined value. So, let us consider values of x that are incredibly close to 0 from the left and right of it.

Let’s try to use the following values:

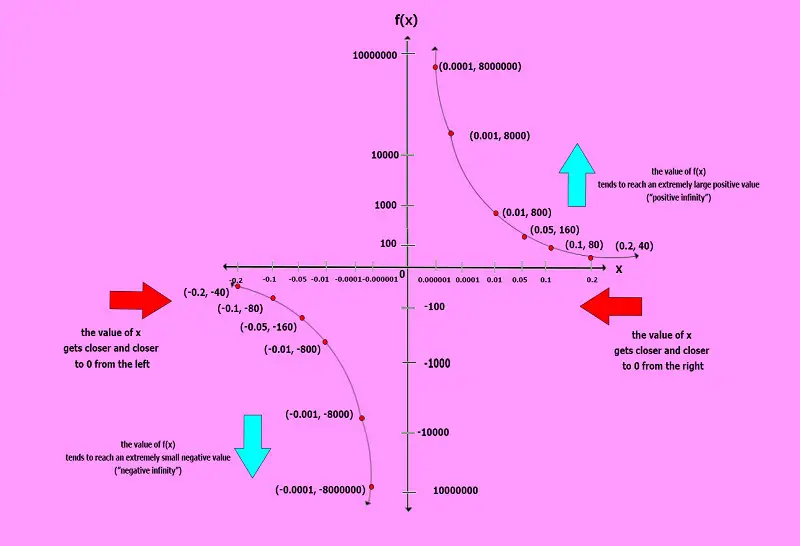
• Values of x extremely close to 0 from the right: x₁ = 0.2, x₂ = 0.1, x₃ = 0.05, x₄ = 0.01, x₅ = 0.0001, x₆ = 0.000001
• Values of x extremely close to 0 from the left: x₁ = -0.2, x₂ = -0.1, x₃ = -0.05, x₄ = -0.01, x₅ = -0.0001, x₆ = -0.000001

Now, let us evaluate the given function with the given values above.

Values of x extremely close to 0 from the right	f(x)	Values of x extremely close to 0 from the left	f(x)
0.2	40	-0.2	-40
0.1	80	-0.1	-80
0.05	160	-0.05	-160
0.01	800	-0.01	-800
0.0001	80000	-0.0001	-80000
0.000001	8000000	-0.000001	-8000000

Notice that as x approaches 0 from the right, the f(x) value becomes larger without bounds. This means that as x tends to reach 0 from the right, f(x) tends to get a huge positive value or the so-called “positive infinity” (Note: “positive infinity” is not a number or a quantitative value; it is just a term we use to state that a positive value is huge).

In symbols,

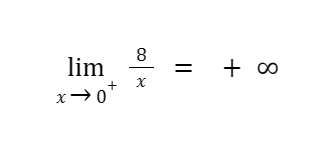
where the symbol “+” above 0 indicates values on the right of 0.

On the other hand, as x approaches 0 from the left, the value of f(x) becomes smaller and smaller without bounds. This means that as x tends to reach 0 from the left, f(x) tends to reach an extremely small negative value or the so-called “negative infinity” (Note: “negative infinity” is not a number or a quantitative value; it is just a term we use to state that a negative value is extremely small).

In symbols,

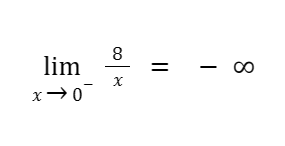
where the symbol “-” above 0 indicates values on the left of 0.

Whether the values of x that are incredibly close to 0 are from the left or the right of 0, the limit of the function is not a specific number. Instead, as x approaches 0 from the left or right, f(x) = 8/x  tends to become extremely large or small. Thus, we can conclude that the limit of this function does not exist. 

In short, if the functional value as x approaches a specific value is not a single number, then we can state that the limit is non-existent. 

There are various types of non-existent limits, but the most commonly encountered ones are infinite limits. Infinite limits imply that the functional values become extremely large or small as x approaches a specific value. 

Our example above,

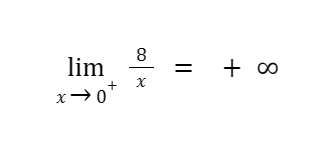
and

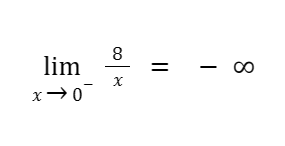
are examples of infinite limits. 

Infinite limits do not tell us that they are infinite values per se; instead, it implies that no single whole number acts as a limit, and the function values tend to become larger and larger (or smaller and smaller) without bounds. 

Evaluating Limits Using Laws of Limits

From the previous section, you learned how to identify the limits of a given function by using a table of values. However, this method is tedious and will consume much of our time.

For this reason, we have to use some mathematical devices to determine the limits of a function. 

Fortunately, mathematicians have already done the hard work and provided us with the laws of limits—the mathematical tools we can use to determine limits. Let us discuss them one by one.

Overview of the Laws of Limits

1. Limit of a Constant Law

“The limit of a constant is the constant itself.”

This law tells us that whatever the value x approaches, the limit of a given constant is always the constant itself. In other words, write the constant, and no need to do calculations.

Sample Problem 1: Evaluate

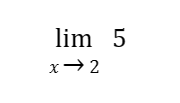
Solution: We are evaluating the limit of a constant (i.e., 5) in this example. The answer is just the constant itself by the limit of a constant law. Thus, the answer is 5.

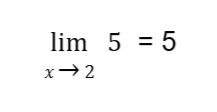
Sample Problem 2: Evaluate

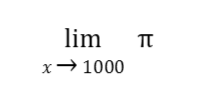
Solution: Note that π is a constant. Therefore, the answer for this example is just π or 

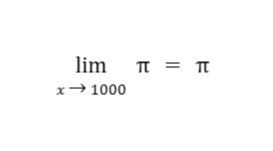
2. Limit of a Variable Law

“The limit of the variable x as x approaches a is just the value of a.” 

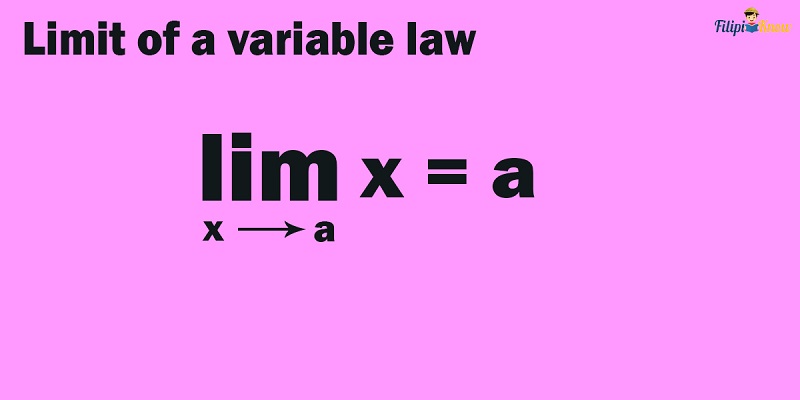
This law tells us that the limit of a specific variable x as x approaches a can be derived by simply replacing x with a.

Sample Problem: Evaluate

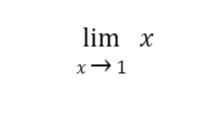
Solution: By the limit of a variable law, we replace x with 1, and the result is the limit. So, 

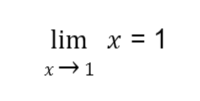
3. Constant Multiple Law

“The limit of the product of a constant and a function is equal to the product of the constant and the limit of the function.”

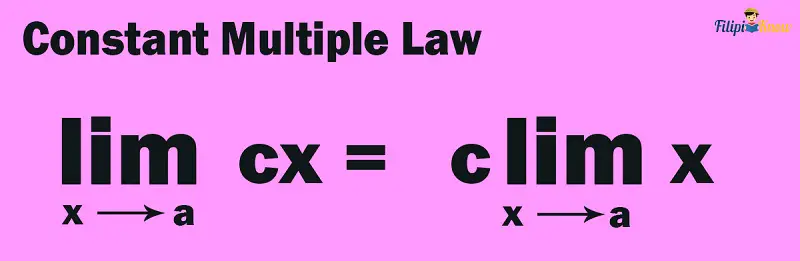
Let us have an example to understand this limit law:

Sample Problem 1: Evaluate

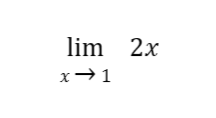
Solution: Note that 2x is the product of 2 and the function or variable x. Hence, by the constant multiple law of limits:

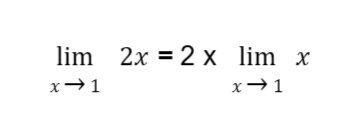
Recall that by the limit of a variable law,

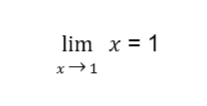
Thus:

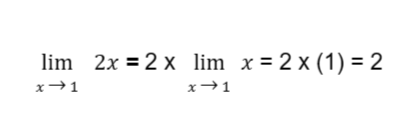
The answer for this example is 2.

Sample Problem 2: Evaluate

Solution: By the constant multiple law of limits:

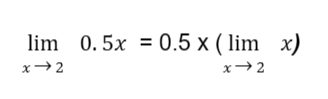
By applying the limit of a variable law,

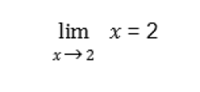
Therefore:

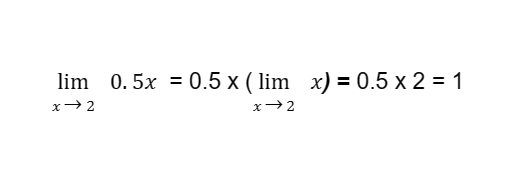
Thus, the answer is 1.

4. Sum Law

“The limit of a sum is equal to the sum of limits.”

We can also apply the sum law when subtraction is involved between limits of quantities.

Sample Problem 1: Evaluate

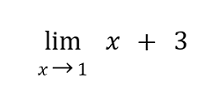
Solution: By the sum law of limits, we can express the limit of a sum as the sum of the respective limits of the addends.

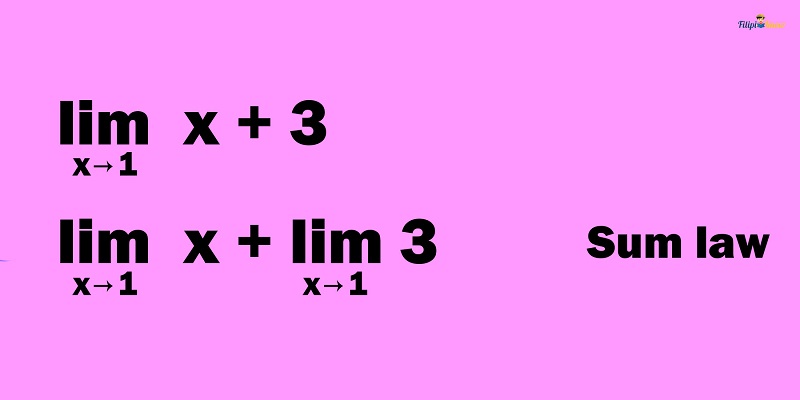
Note that by the limit of a variable law, the

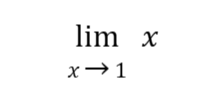
can be derived by letting x = 1, so,

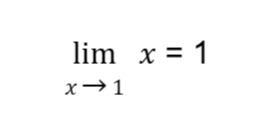
Meanwhile, by the limit of a constant law, the

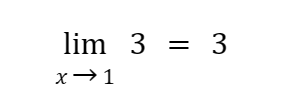
Hence:

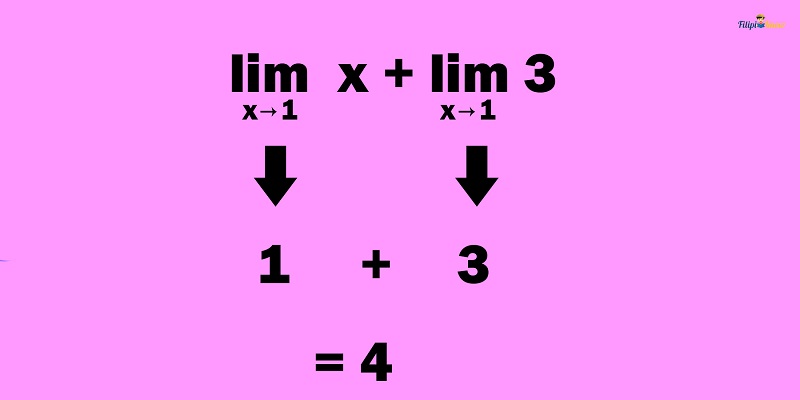
Therefore,

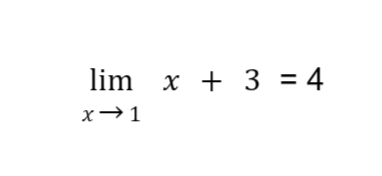
Sample Problem 2: Evaluate

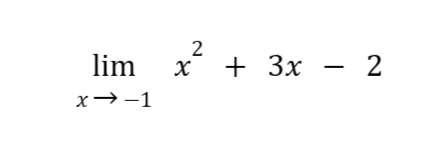
Solution:

By applying the sum law of limits:

By using the limit of a variable law and the limit of a constant law:

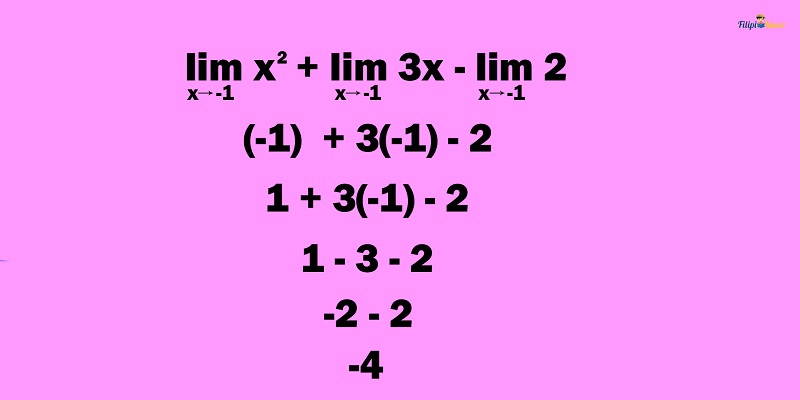
Therefore,

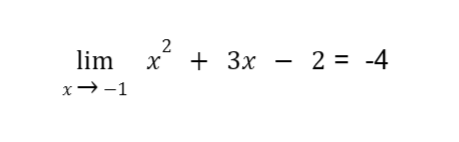
Sample Problem 3: Determine the limit of 2x² – 3 as x approaches 0.5

Solution:

Thus, the limit of 2x² – 3 as x approaches 0.5 is -2.5.

5. Product Law

“The limit of the product of functions is equal to the product of the limits of the functions.”

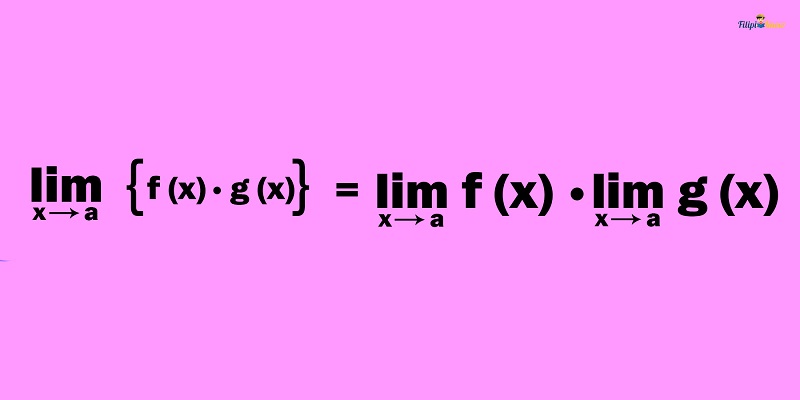
This law is quite intuitive and self-explanatory. We can rewrite the limit of a product as the product of the limits.

Sample Problem: Evaluate

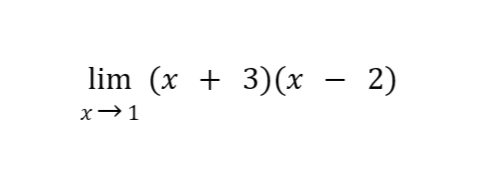
Solution: By applying the product law, we can express the limit of the product of x + 3 and x – 2 as the product of the respective limits of x + 3 and x – 2.

Let us continue evaluating the limit by applying the limit laws we have learned earlier:

Thus, the answer to this problem is -4.

6. Quotient Law

“The limit of the quotient of functions is equal to the quotient of the limits of the functions.”

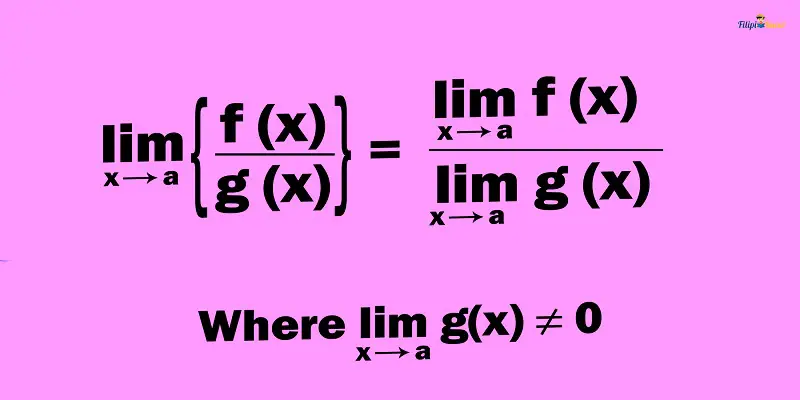
Quotient law is similar to product law, but we now deal with division instead of multiplication. Through this law, we can rewrite the limit of a quotient as the quotient of the limits. 

Sample Problem: Evaluate

Solution: By applying the quotient law, we can express the limit of the quotient of x + 3 and x – 2 as the quotient of the respective limits of x + 3 and x – 2:

Let us continue evaluating the limit by applying the limit laws we have learned earlier:

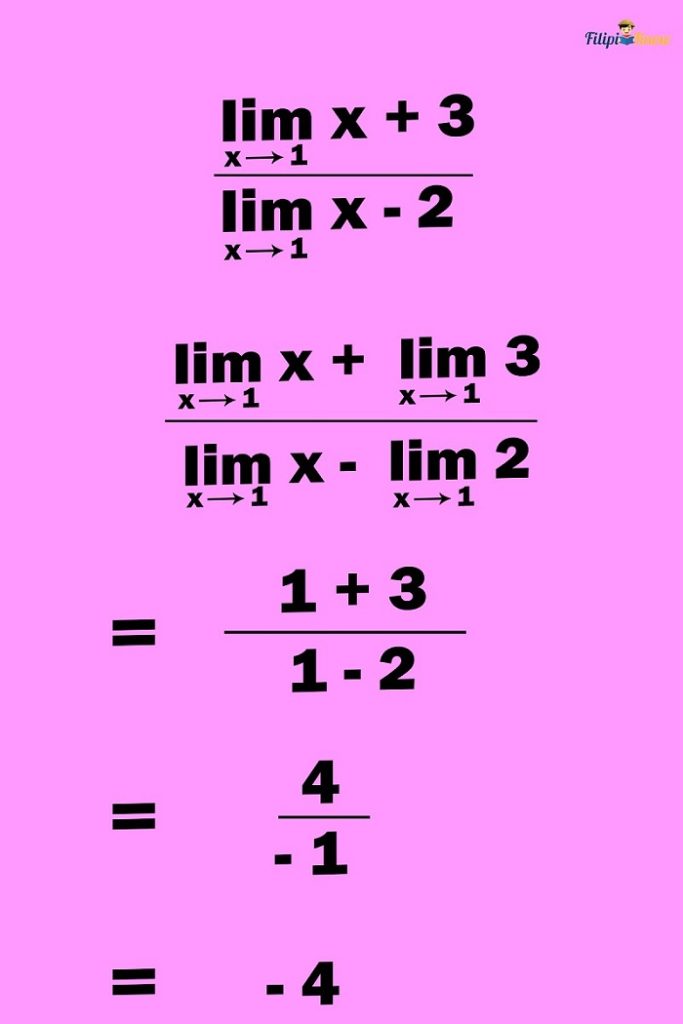
Thus, the limit is -4.

Evaluating Limits Using the Substitution Method

In the previous section, you have learned how to evaluate the limit of a function by applying the limit laws. However, you might have realized that using the laws is still tedious since you must write the limit notation repeatedly. 

In this section, you are going to learn how to evaluate the limit of a function through a substitution method, which allows you to substitute a to x to find the limit of f(x) as x approaches a:

However, you can only apply the substitution method if the limiting value is an element of the domain of the function or if that value of x will not make the function undefined.

Let us apply the substitution method to find the limit of x² – 2x + 1 if x approaches 1. 

Using the limit laws for this case will be pretty fast but tedious since we have to write the limit notation repeatedly. The limiting value, 1, is part of the domain of x² – 2x + 1; it will not make the value of the function undefined if we substitute it. Therefore, we can use the substitution method to find the limit of the given function:

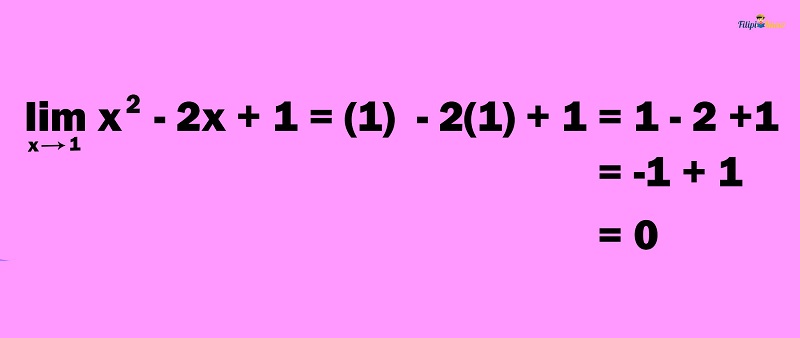
Hence, the answer is 0.

Sample Problem 1: What is the limit of the function f(x) = 2x – 5 as x approaches -2?

Solution: We can apply the substitution method for this case since the limiting value of -2 will not make the function undefined.

By substitution method:

2(-2) – 5 

-4 – 5 = -9

Hence, the answer is -9.

Sample Problem 2: Determine the limit of the function f(x) = 4x – x² as x approaches ½ .

Solution:  We can apply the substitution method for this case since the limiting value of ½  will not make the function undefined.

       f(x) = 4x – x²

Substituting x = ½: 

4(½ ) – (½ )²

Note that (½)² = ½ x ½ = ¼. So, we have:

2 – ¼ 

We must make the denominators similar to find the difference between 2 and ¼.

8/4 – 1/4

= 7/4 

Thus, the answer is 7/4.

However, there are some cases where the substitution method cannot be used directly to evaluate limits. 

For instance, if we try to determine the limit of

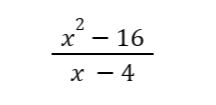
as x approaches 4, we cannot use the substitution method directly because if we substitute x = 4 to the function, we will have a 0 denominator, leading to a value that is not a real number. Hence, we cannot use the substitution method for this case. 

In the succeeding section, you will learn how to evaluate the limits of functions when the substitution method does not apply to them.  

Evaluating Limits Using the Factoring Method

If we cannot apply the substitution method to identify the limit of a function, one method we can use is the factoring method.

Retake a look at the function below.

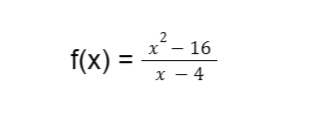
Let’s try to identify the limit of this function as x approaches 4. Suppose that we use the substitution method to find the limit.

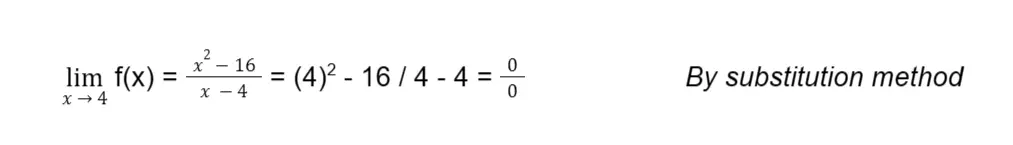
The substitution method fails to find the limit of the function. We have obtained 0/0, which is not a real number.  0/0 is one of the so-called indeterminate forms in calculus.

Limits in the indeterminate form 0/0 can be solved using the factoring method.

Sample Problem 1: Can we use the factoring method for these limits?

Solution: 

The factoring method can solve the limit in (a) since it is in the indeterminate form 0/0 if we substitute x = -2 to the function.

The factoring method can solve the limit in (b) since it is in the indeterminate form 0/0 if we substitute x = -5 to the function.

The factoring method cannot solve the limit in (c) since it will not result in an indeterminate form 0/0 if we substitute x = 0 to the function. If we substitute x = 0, we will obtain 5/0 instead, which is not the indeterminate form 0/0. 

Using the factoring method to evaluate limits in indeterminate form 0/0, we factor the expression in the numerator or the denominator, cancel the common factor, and then apply the substitution method.

Sample Problem 2: Evaluate

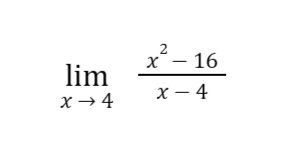
Solution: The given limit is indeterminate 0/0 if we substitute x = 4 to the function.

Note that we can factor x² – 16 as (x + 4)(x – 4) (factoring difference of two squares):

We can cancel out the common factor x – 4:

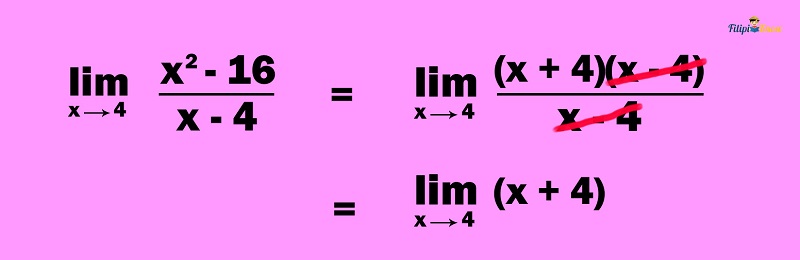
Lastly, we apply the substitution method:

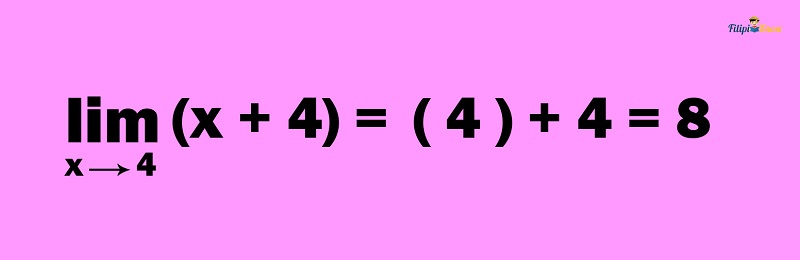
Therefore,

Sample Problem 3: Evaluate

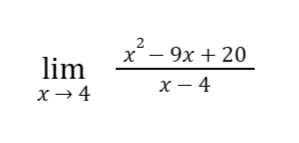
Solution: The given limit is indeterminate 0/0 if we substitute x = 4 to the function.

Thus, we can solve the given limit by factoring in the following:

Therefore, the limit is -1.

Sample Problem 4: Evaluate

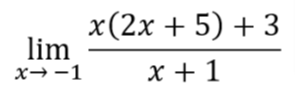
Solution: By the distributive property, we can rewrite the given function as

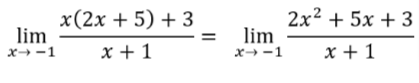
Thus, we are just basically determining or evaluating

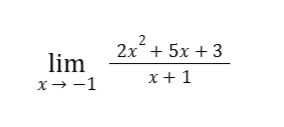
If we substitute x = -1 to the function, we will obtain the indeterminate form 0/0. Thus, we can use the factoring method to solve for the limit.

The answer to this problem is 1.

Infinite Limits

In the earlier section, we discussed what infinite limits are. Essentially, this happens when we get the limit of a function as x approaches a particular value, but it never gets closer to a real number. What’s happening is that the value of f(x) tends to get larger or smaller.

An infinite limit means the limit also does not exist. 

Sample Problem: Consider

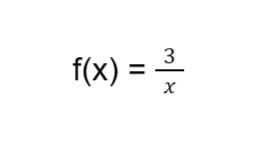
What is the limit of f(x) as x approaches 0?

Solution: We cannot use substitution or factoring methods for this case. First, 0 will make the function undefined and not lead to an indeterminate form 0/0 if we substitute it (3/0 instead). 

So, how do we identify its limit without using an exhaustive table of values?

Here’s our technique: 

We substitute values of x close to 0, one from the right of 0  (greater than x) and one on the left of 0 (less than 0). 

For the left of 0, let us use -0.001 (the symbol “-” above 0 in the limit below indicates that we are using a value of x on the left of 0).

Notice that the value we have obtained is a small negative number. If we try substituting a value much closer to 0, we will surely obtain a much smaller negative number. Then, we can state that as x approaches 0 from the left, the f(x) value becomes smaller without bounds. 

Meanwhile, for the right of 0, if we use 0.001 (the symbol “+” above 0 in the limit below indicates that we are using a value of x on the right of 0).

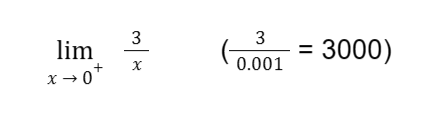
Notice that the value we have obtained is a large positive number. If we try substituting a value much closer to 0, we will get a much larger positive number. Then, we can state that as x approaches 0 from the right, the value of f(x) becomes larger and larger without bounds. 

We can summarize our observation below:

Where c is a positive real number. 

In our next chapter, you will learn differentiation – the heart of calculus. The concept of the limits of functions is the building block to understanding differentiation. Hence, we advise you to keep reading this review to absorb the concepts and prepare for the next chapter. 

Next topic: Basic Differentiation

Previous topic: Graph Analysis

Return to the main article: The Ultimate Basic Math Reviewer

Download Printable Summary/Review Notes

Download Printable Flashcards

Test Yourself!

1. Practice Questions [Free PDF Download]

2. Answer Key [Free PDF Download]

3. Math Mock Exam + Answer Key