Functions in General Math: A Review

If one variable’s value depends on another variable’s value, then we can use functions to analyze them. 

Functions can be applied to describe and analyze the following real-life scenarios:

• The cost you have to pay after shopping depends on the number of items you bought
• The amount of gasoline consumed depends on the distance traveled by the car
• The monthly sales of a restaurant depend on the number of dishes it sells

This review explores the mathematics of functions, including their definition, operations, and related concepts.

Click below to go to the main reviewer:

Ultimate UPCAT Reviewer

Ultimate NMAT Reviewer

Ultimate PMA Entrance Exam Reviewer

Ultimate LET Reviewer

Introduction to Functions: Relations, Independent Variables, and Dependent Variables

Before you learn a function, you must understand the concept of relations, independent variables, and dependent variables.

1. Relations

Suppose that you have two sets. Set A consists of three persons: Ana, Ben, and Carlo. Meanwhile, Set B consists of red, blue, and yellow colors.

Ana’s favorite color is yellow, Ben’s favorite colors are blue and yellow, and Carlo’s favorite colors are red and yellow.

We can create a diagram that connects Set A and Set B. The connecting lines represent the persons in Set A and the corresponding colors they like in Set B.

For instance, the line that connects Ana (an element of Set A) and yellow (an element of Set B) means that Ana likes yellow.

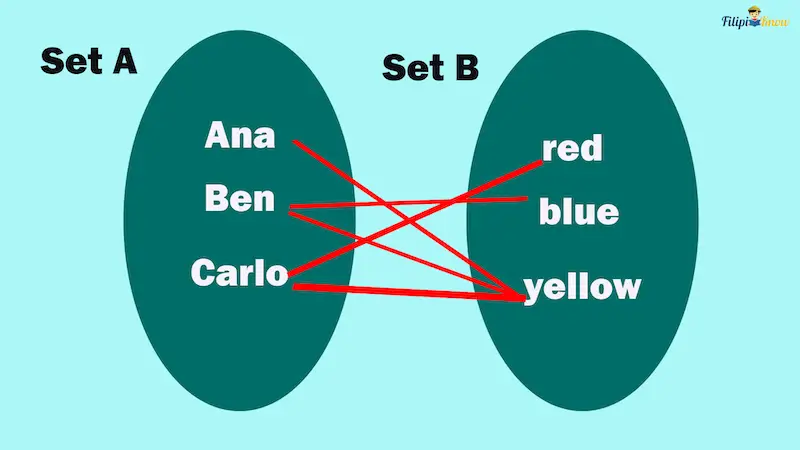
We can also write the illustration above as a set of ordered pairs in the format (PERSON, FAVORITE COLOR). We call this set P:

P = {(Ana, yellow), (Ben, blue), (Ben, yellow), (Carlo, red), (Carlo, yellow)}

Note that the ordered pair’s first component corresponds to a person in set A, while the second corresponds to the person’s favorite color. For instance,(Ben, yellow) means that Ben’s favorite color is yellow.

Set P is an example of a relation. A relation is a set that consists of ordered pairs.

Furthermore, set P tells us that sets A and B are related. Each element of set A (Ana, Ben, and Carlo) has a corresponding match in set B (red, blue, yellow). For instance, Ana (an element of set A) is matched to yellow (an element of set B). 

Example: A small shop operates from Monday to Friday. The table below shows the daily number of customers of the shop:

Day	Number of customers
Monday	10
Tuesday	8
Wednesday	12
Thursday	9
Friday	15

We can illustrate the given situation above as a diagram as shown below:

Let us write the illustration above as a set of ordered pairs. For instance, the ordered pair (Monday, 10) means that, on Monday, the shop had ten customers. Let us call this set Z:

Z = {(Monday, 10), (Tuesday, 8), (Wednesday, 12), (Thursday, 9), (Friday, 15)}

Z is an example of a relation since it is a set of ordered pairs.

Z presents ordered pairs with the first coordinates referring to a specific day the shop operates and the second coordinates referring to the number of customers they had on the day indicated on the first coordinate.

All the first components of a relation are called inputs. On the other hand, all the second components of a relation are called outputs. 

For instance, Monday is an input of the relation Z, while 10 is an output of the same relation. 

In a relation, the value of outputs depends on the value of inputs. Thus, in set Z, the number of customers depends on what day the shop operates. 

Think of set Z as a machine that, when you input a specific day, you will get a particular output: the number of customers. For instance, if we input Wednesday, we obtain 12 as the number of customers. If we input Friday, we obtain 15 as the number of customers. This is what we mean when we say the number of customers depends on what day the shop operates. 

2. Independent and Dependent Variables

Let us retake a look at our previous example about the small shop:

Day	Number of customers
Monday	10
Tuesday	8
Wednesday	12
Thursday	9
Friday	15

In this given situation, we have two variables. First, we have the working day (or day) as a variable. It is variable since a working day can take a specific value: Monday, Tuesday, Wednesday, etc. The second variable is the number of customers, which can also take values depending on the shop’s day.

Now, recall that the number of customers depends on the working day. Hence, we call the variable “number of customers” the dependent variable. A dependent variable is a variable whose values depend on the other variable. On the other hand, the day the shop operates is the independent variable. The value of an independent variable does not depend on the value of another variable.

Recall our relation

Z = {(Monday, 10), (Tuesday, 8), (Wednesday, 12), (Thursday, 9), (Friday, 15)}

The inputs of a relation or the first component of the relation are the values of the independent variable. Meanwhile, the outputs of a relation or the second component of the relation are the values of the dependent variable. A specific value of the independent variable (input) will give you a specific value of the dependent variable (output).

Example 1: Determine the dependent and independent variables of the following situation:

a. A student’s score in his exam depends on the number of hours he studied

b. The profit of an entrepreneur depends on the number of items he sells

c. The number of participants in a conference tells the number of seats to be prepared by the organizers of the conference

Solution:

a. Independent variable: number of hours the student studied; dependent variable: the student’s score in his exam

b. Independent variable: number of items sold; dependent variable: profit of the entrepreneur

c. Independent variable: number of participants in a conference; dependent variable: number of seats to be prepared

Example 2: A phone’s battery level depends on how many hours it was charged. If the phone is charged for 2 hours, its battery level is 80%. Determine the independent variable, dependent variable, input, and output of this given problem.

Solution: The dependent variable is the phone’s battery level since its value depends on how long or how many hours that phone was charged. The independent variable is the number of hours the phone was charged since it dictates its battery level.

The input in the given situation is 2 hours since it is a value of the independent variable (number of hours). Meanwhile, 80% is the output since it is a value of the dependent variable (battery level).

 

Functions

A function is a relation wherein the first components of the ordered pairs are assigned or matched to only a single second component. 

This implies that in a function, each value of the independent variable (input) gives a unique corresponding value of the dependent variable (output). 

A quick way to determine if a set of ordered pairs is a function is if there’s no first component repeated in the set.

Let us take a look at set Z:

Z =  {(Monday, 10), (Tuesday, 8), (Wednesday, 12), (Thursday, 9), (Friday, 15)}

Set Z is a function since no first component is repeated in the set.

On the other hand, let us take a look at set P:

P = {(Ana, yellow), (Ben, blue), (Ben, yellow), (Carlo, red), (Carlo, yellow)}

Set P is not a function because the first component of an ordered pair is repeated. In particular, the first components, Ben and Carlo, were repeated. This implies that certain values of the independent variable (person) have different corresponding values of the dependent variable (favorite color). 

Example: Which of the following relations is/are functions?

a. J = {(0, 1), (2, 1), (3, 2)}

b. K = {(5, 1), (5, 2), (5, 3)}

c.

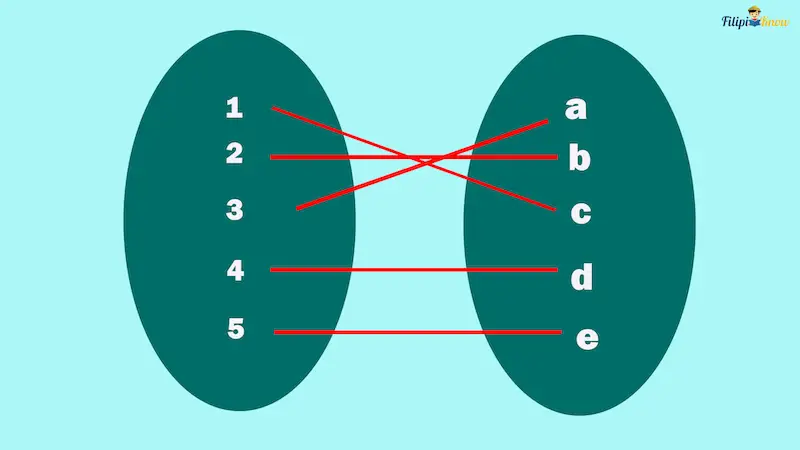
d.

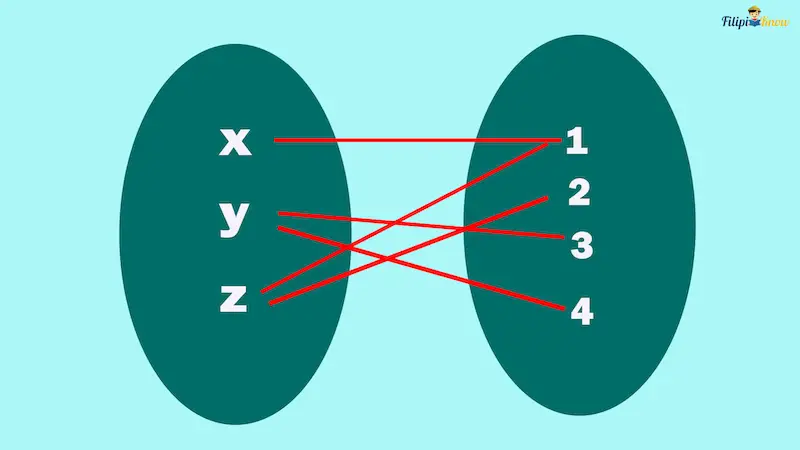
Solution:

a. J is a function since no first component of ordered pairs is repeated.

b. K is not a function since the first component of ordered pairs is repeated (5 is assigned to three different second components).

c. The diagram shows an example of a function since we can write the pairs as: (1, c), (2, b), (3, a), (4, d), (5, e). No inputs are repeated or matched with two different outputs.

d. The diagram is not a function since two of the first components are matched to two different second components. If we write the given diagram into a set of ordered pairs, we’ll obtain (x, 1), (y, 3), (y, 4), (z, 2), (z, 1). Notice that y and z (the first components) are matched with two different second components.

Functions and Relations

It is important to remember that all functions are relations, but not all relations are functions.

For instance, the set of ordered pairs {(1, 2), (2, 4), (3, 6), (4, 8)} is a function (since there is no first component of ordered pairs that is repeated). This automatically implies that the set is also a relation. 

Meanwhile, {(2, 5), (2, 7), (1, 0), (-4, 8)} is not a function because there is an input (which is 2) that is repeated or has two different corresponding outputs. However, the set is still a relation since it is a set of ordered pairs.

Lastly, the set {0, 1, 2, 3} is neither a relation nor a function.

 

Independent and Dependent Variable of a Function

Since a function is a relation, we expect it to have an independent and dependent variable.

Let us take a look at Letty’s shop list of items and their corresponding prices:

Item	Price
Bracelet	₱30
Necklace	₱50
Handkerchief	₱25
Keychain	₱15

We can express the given table above as a set of ordered pairs matching each item to its corresponding price:

{(Bracelet, 30), (Necklace, 50), (Handkerchief, 25), (Keychain, 15)}

The set above is an example of a function since there’s no first component assigned to two different second components.

In this situation, the price is the dependent variable because its value depends on the type of item. Meanwhile, the type of item is the independent variable because its value dictates the dependent variable’s value.

Let us have another example.

Example: A small milk tea shop earns ₱40 for every milk tea sold, ₱80 if it sells two milk teas, ₱120 if it sells three milk teas, and so on. 

Solution: In this situation, the sales of the milk tea shop are the dependent variable since its value depends on how many milk teas the shop will sell. This implies that the number of milk teas sold is the independent variable since the number of milk teas sold dictates the value of the sales (or dependent variable).

We can express the given set of ordered pairs matching the number of milk teas sold to the number of sales as:

{(1, 40), (2, 80), (3, 120)}

As we can see, the set above is a function.

The dependent variable is a function of the independent variable. This means that to obtain the value of the dependent variable, we must first have the value of the independent variable and use it to generate the value of the dependent variable.

In other words, the value of the independent variable (input) determines the dependent variable’s (output) value.

In our example, the sales of the milk tea shop are a function of the number of milk teas sold.  This means that the value of the number of milk teas sold will generate the sales of the milk tea shop.

Function Notation

In a function, we usually use x to represent the independent variable and y as the dependent variable. Using the same example above, we can express the dependent variable “sales” as y and the independent variable “number of milk teas sold” as x.

We have stated that the sales of the milk tea shop are a function of the number of milk teas sold. In function notation, we express it as: y = f(x)

The symbol f(x) is read as “f of x.”

The expression tells us that if we put a certain value of x (or independent variable), the function (represented by f) will generate a value of y (dependent variable). For instance, in our milk tea shop example, if we let x = 2, the function will give us y = 80. In function notation:

y = f(x)

80 = f(2) Let x = 2

We can think of y = f(x) as a machine. The function’s input is the value of the independent variable; once we insert it into the function, the function will generate and produce the value of the dependent variable, which is the function’s output.

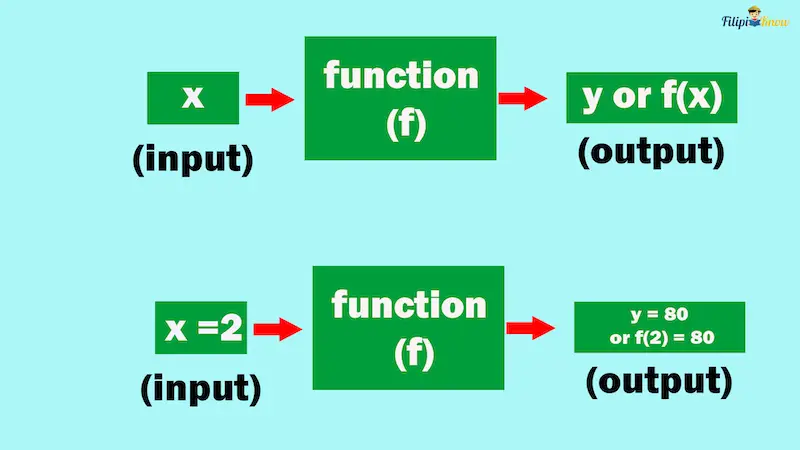
When x = 2, the function gives a value of y = 80. 

We can also express it as an ordered pair (2, 80).

Example 1: The amount of gasoline (g) consumed by a car in liters is a function of the distance (d) traveled by car in km. Express this in function notation and determine the independent and dependent variables.

Solution: In this situation, the amount of gasoline consumed is the dependent variable, while the distance traveled by car is the independent variable. In function notation:

g = f(d)

Example 2: Using the function notation above, what does 2 = f(5) mean?

Solution: Since g = f(d), 2 = f(5) means that 5 km traveled by car consumes 2 liters of gasoline.

We can express this as an ordered pair (5, 2).

Algebraic Form of a Function

To provide a more precise description of a function, we express it algebraically.

For instance, f(x) = 2x + 1 is an example of a function in algebraic form.

If we input a value of x (or independent variable) in this function, we obtain a value for y or f(x) (recall that y = f(x)).

Say we input x = 1 to the function f(x) = 2x + 1. This means that if we substitute x = 1 to the function:

f(x) = 2x + 1

f(1) = 2(1) + 1 Substitute x = 1

f(1) = 2 + 1

f(1) = 3

We have obtained 3. This means that we obtain three as the output when we input x = 1 to the function f(x) = 2x + 1.

We can express what we have just obtained as an ordered pair (1, 3).

The table below presents what we will obtain if we input different values of x to the function f(x) = 2x + 1.

x	y = f(x)
1	3
2	5
3	7
4	9

We can write the table above as a set of ordered pairs: {(1, 3), (2, 5), (3, 7), (4, 9)}.

Notice that all x or first components correspond to only one second component. This is because we have evaluated a function, particularly f(x) = 2x + 1.

Evaluating a Function

Evaluating a function means inputting a value of the independent variable (or x) to the function to obtain a corresponding dependent variable (or y) value.

Example 1: Evaluate f(x) = x² + 2x at x = 0.

Solution:

f(x) = x² + 2x

f(0) = (0)² + 2(0) Input x = 0 to the function

f(0) = 0 The output value we obtain is 0

Thus, the value of the function is 0 when we input x = 0 to it. 

Example 2: What is f(-1) if f(x) = x – 9?

The symbol f(-1) tells us we must substitute or input x = -1 to the function.

Solution:

f(x) = x – 9

f(-1) = (-1) – 9 Input x = -1

f(-1) = -10

Thus, the value of the function is -10 when we input x = -1 to it.

Example 3: A video game company’s annual sales in ₱ is a function of the number of copies of video games sold in the market. It is described algebraically by the function S(x) = 450x + 10000, where x is the number of copies sold. Suppose that in 2012, the number of video games sold was 13,000. How much were the company’s annual sales in 2012?

Solution:

Given the function S(x) = 450x + 10000, the annual sales in 2012 can be determined by inputting x = 13000 (i.e., the number of copies of video games sold) into the given function:

S(x) = 450x + 10000

S(13000) = 450(13000) + 10000 Input x = 13000

S(13000) = 5,860,000

Hence, in 2012, the video game company generated annual sales of ₱5,860,000.

 

Domain and Range of a Function

1. Domain of a Function

The domain of a function is the set of all possible values of the independent variables in a function.

In other words, these are all the possible inputs of a function or possible values of x. 

Also, the domain of a function is the set of all values of x that will give you a value of y that is a real number.

We can quickly tell the domain of a function if it is in set form.  For instance, the domain of the function {(1, 0), (2, 1), (3, 5)} is just 1, 2, 3 since these are the inputs of the function (recall that the first components of a set of ordered pairs are the inputs).

We want to express the domain as a set. So to correctly answer the given example above, the domain of the set is D = {1, 2, 3}.

However, it is a bit difficult to determine the domain of a set if the function is expressed algebraically. This is what we are going to discuss in the next section.

How To Determine the Domain of a Function

The simplest things to consider when determining the domain of a function are:

1. The denominator of the function must not be 0.
2. The value under the square-root sign of the function must be nonnegative (0 or positive).

If the output of a function is always a real number for any real number you input into the function, then the function’s domain is the set of real numbers.

Example 1: Determine the domain of the function f(x) = 2x + 1.

Solution: Since the given function has no denominator and square root sign, the domain of f(x) = 2x + 1 is the set of all real numbers. This means that whatever real number you substitute for x, the value of y or f(x) will always be a real number.

We can write the set of real numbers as the domain in this set notation form:

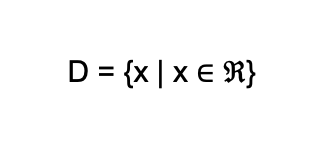
This is read as “the domain is the set of all x such that x is an element of the set of real numbers,” with the last symbol being the set of real numbers.

Example 2: What is the domain of the function f(x) = x² – 5x + 6?

Solution: Since the given function has no denominator and square root sign, the f(x) = x2 – 5x + 6 domain is the set of all real numbers. This means that whatever real number you substitute for x, the value of y or f(x) will always be a real number.

In set notation form,

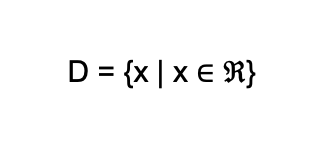
Example 3: Determine the domain of

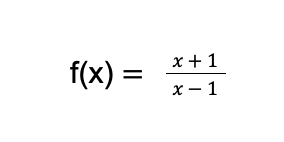
Solution: This time, the given function has a denominator of x – 1. To determine the domain of this function, let us first determine the value of x that will make the denominator x – 1 equal to 0.

We can set up an equation:

x – 1 = 0

x = 1 Transposition method

Thus, at x = 1, the denominator of the given function is 0.

The value of x that will make the denominator 0 will be the value excluded in the domain. Hence, the function’s domain is the set of all real numbers except 1. 

Any number you substitute to x will give you a real number value of function except for 1 because, at x = 1, the denominator will be 0 (which is not allowed since division by 0 is undefined).

In set notation form,

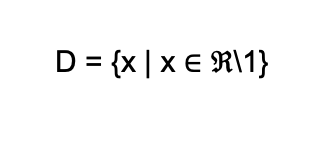
This is read as “the domain is the set of all x such that x is an element of the set of real numbers except 1.”

Example 4: Determine the domain of

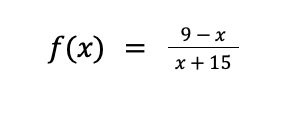
Solution: We need to find the number that must be excluded from the domain. That number is what will make the denominator 0.

x + 15 = 0

x = -15 Transposition method

Therefore, the domain is the set of all real numbers except -15.

In set notation form,

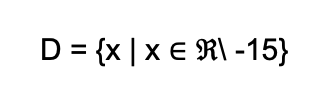
Example 5: What is the domain of

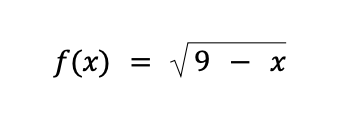
Solution: The given function has a square root sign. To find the domain of this function, we must find all values of x that will make the radicand (the quantity under the radical sign) nonnegative.

Why do we need to make the radicand nonnegative? Because if the radicand is negative, we have a square root of a negative number which is an imaginary number and not a real number.

This means that we need to find the values of x such that 9 – x will be nonnegative or greater than or equal to 0.

Thus, the function’s domain is the set of all real numbers less than or equal to 9. This means that if you try to substitute a value of x greater than 9, the value of the function will not be a real number (try to substitute x = 10 to the function and see what will happen).

In set notation form,

D = { x | x ≤ 9} 

Example 6: Determine the domain of the function

Solution: As you can see, the given function has a denominator and a square root sign, making it quite tricky.

Let us work for the domain of this function using the considerations one by one:

Starting with the numerator, recall that if we have a square root sign, the radicand must be nonnegative:

x – 2 ≥ 0

x ≥ 2 Transposition method

Thus, part of our domain is the set of all real numbers greater than 2.

We’re not done yet; we also need to consider the denominator.

The denominator must not be zero, so we have the following:

x – 8 = 0

x = 8 Transposition method

Thus, we should exclude x = 8 from the domain since it will give a denominator value of 0.

Note that we obtained x ≥ 2 earlier and discovered that x = 8 should be excluded from the domain. Therefore, our domain should be x ≥  2 \ 8, or the set of all real numbers greater than 2 but 8 is not included.

In set notation form,

D = {x | x ≥ 2 \ 8} 

2. Range of a Function

The range of a function is the set of all possible values of the dependent variable.

In other words, these are all the possible outputs of the function or the values of y or f(x).

Again, if the function is written as a set of ordered pairs such as {(1, 0), (2, 1), (3, 2)}, the range is R = {0, 1, 2} since these are the outputs of the function.

The range of a function expressed algebraically depends on its type. For instance, the range of a linear function is simply the set of all real numbers. However, functions such as quadratic, absolute value, and rational functions have their own set of rules to determine the range.

 

Operations on Functions

This section will discuss adding, subtracting, multiplying, and dividing functions. Since functions are expressed algebraically, your knowledge of how to perform fundamental operations with polynomials and rational expressions will help you perform the operations with functions.

1. Addition and Subtraction of Functions

As the figure above shows, we can add/subtract the terms of the functions to obtain their sum/difference.

The symbol (f + g)(x) means the sum of functions f(x) and g(x). On the other hand, the symbol (f – g)(x) means the difference between the functions f(x) and g(x).

Example 1: If f(x) = x + 3 and g(x) = x + 5, what is (f + g)(x)?

Solution:

(f + g)(x) = f(x) + g(x) 

(f + g)(x) = (x + 3) + (x + 5)

(f + g)(x) = 2x + 8

The answer is (f + g)(x) = 2x + 8

Example 2: Determine (f + g)(1) using the same functions in the previous example.

Solution:

The symbol (f + g)(1) means that we need to input 1 to the sum function (f + g)(x).

Recall that we obtain (f + g)(x) = 2x + 8 in the previous example.

Hence, to determine (f + g)(1):

(f + g)(x) = 2x + 8

(f + g)(1) = 2(1) + 8

(f + g)(1) = 2 + 8

(f + g)(1) = 10

Thus, (f + g)(1) = 10

Example 3: If f(x) = 5x – 2 and g(x) = 3x + 4. Determine (f – g)(2).

Solution:

Let us start by determining (f – g)(x) first:

(f – g)(x) = f(x) – g(x)

(f – g)(x) = (5x – 2) – (3x + 4)

(f – g)(x) = (5x – 2) + (-3x – 4)

(f – g)(x)  = 2x – 6

Thus, (f – g)(x)  = 2x – 6. To find (f -g)(2), we input x = 2 to the difference function:

(f – g)(2) = 2(2) – 6

(f – g)(2) = 4 – 6

(f – g)(2) = -2

Therefore, the value of (f – g)(2) is -2.

Example 4:

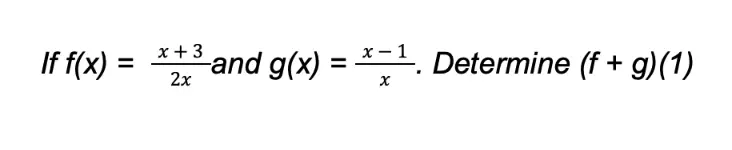
Solution:

Since the functions are in the form of rational expressions, we add the terms of the function, just like what we do with rational expressions (Note that the rational expressions are dissimilar, so we have to transform them into similar rational expressions first):

Now, let us input x = 1 to the sum function to determine (f + g)(1):

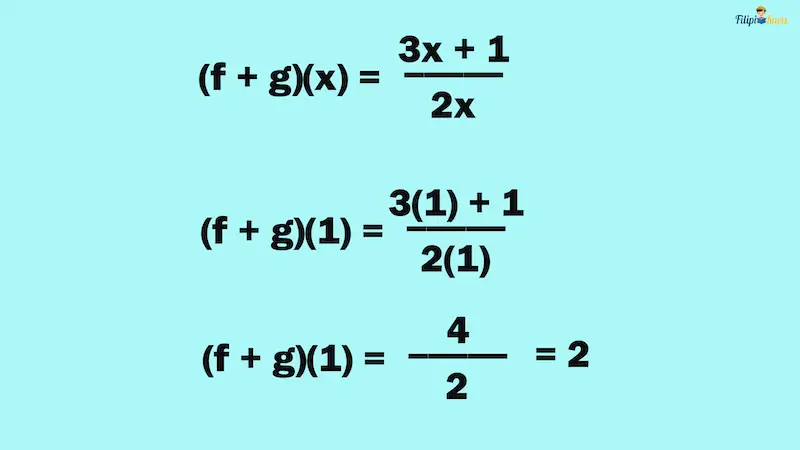
2. Multiplication of Functions

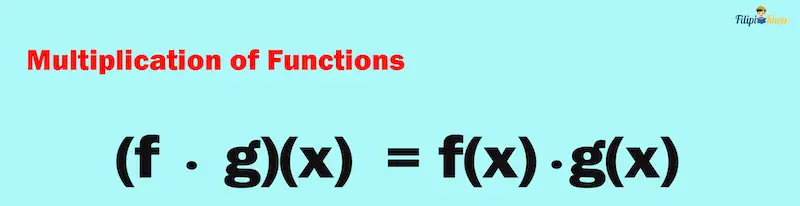
We can multiply their terms to find the product of functions, just like polynomials.

The symbol (f ⋅ g)(x) means the product of the functions f(x) and g(x). 

Example 1: If f(x) = 3x and g(x) = x + 1, determine (f ⋅ g)(x).

Solution:

Since (f ⋅ g)(x) = f(x) ⋅ g(x), then:

(f ⋅ g)(x) = f(x) ∙ g(x)

(f ∙ g)(x) = 3x(x + 1)

(f ∙ g)(x) = 3x² + 3x

Thus, (f ∙ g)(x) = 3x² + 3x

Example 2: If f(x) = x – 1 and g(x) = x + 4, what is (f ∙ g)(-1)?

Solution:

To find (f ∙ g)(-1), we need to determine (f ∙ g)(x) first:

(f ∙ g)(x) = f(x) ∙ g(x)

(f ∙ g)(x) = (x – 1)(x + 4)

(f ∙ g)(x) = x² + 3x – 4 Using FOIL method

Now, we have obtained (f ∙ g)(x) = x² + 3x – 4 as the product function. To determine (f ∙ g)(-1), we need to input x = -1 to the product function:

(f ∙ g)(x) = x² + 3x – 4

(f ∙ g)(-1) = (-1)² + 3(-1) – 4

(f ∙ g)(-1) = 1 – 3 – 4

(f ∙ g)(-1) = -6

Therefore, (f ∙ g)(-1) = -6 is the answer.

Example 3:

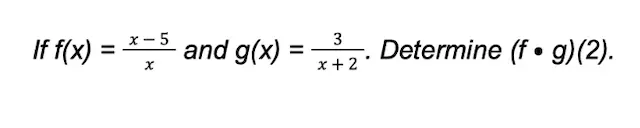
Solution:

To find (f ∙ g)(2), we have to discover first what is (f ∙ g)(x). We do this by multiplying the given functions:

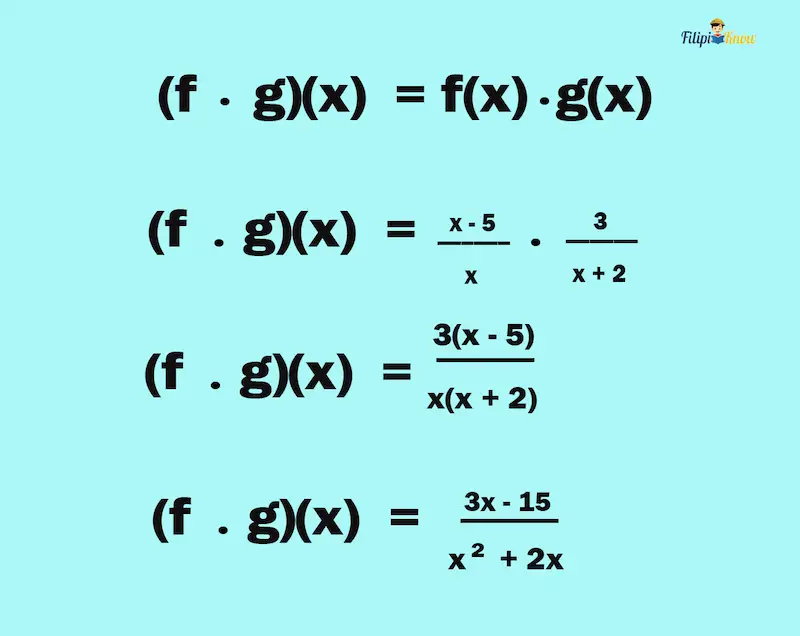
Now, to determine (f ∙ g)(2), we input x = 2 to the product function:

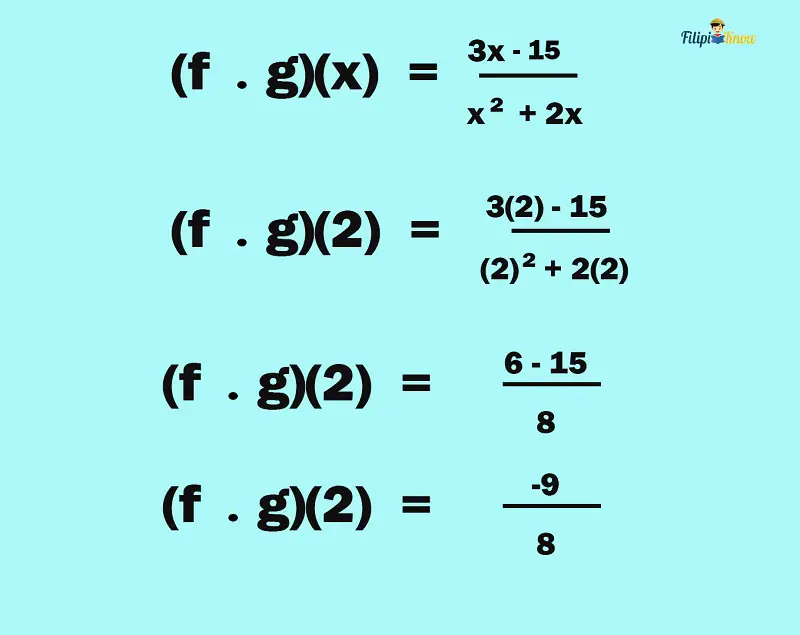
Hence, (f ∙ g)(2) = -9/8

3. Division of Functions

To divide functions, we divide the corresponding terms of the function just like we do with polynomials or rational expressions.

The symbol (f⁄g)(x) means the quotient of the functions f(x) and g(x) or f(x)⁄g(x).

Example 1: If f(x) = 8x² + 4x and g(x) = 2x, determine (f⁄g)(x).

Solution:

To find (f⁄g)(x), we have to divide the function f(x) by g(x):

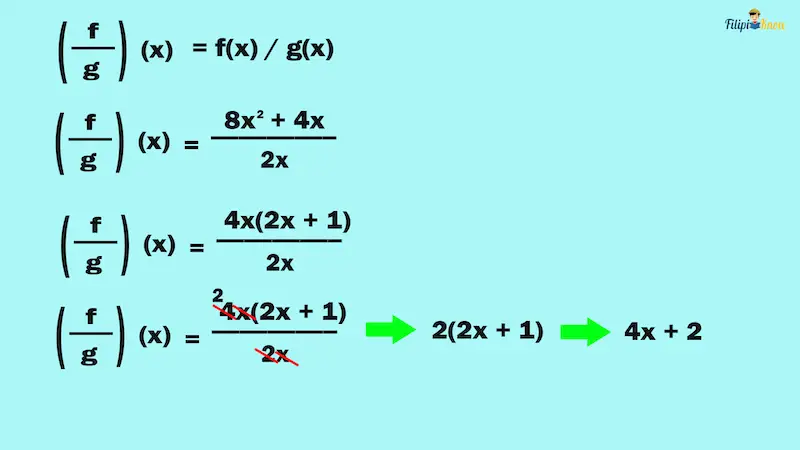
Thus, the answer is (f⁄g)(x)=  4x + 2

Example 2: Determine (f/g)(-1) using the same functions in the previous example.

Solution:

The quotient function obtained in the previous example is (f⁄g)(x) = 4x + 2. To find (f⁄g)(-1), we must substitute or input x = -1 to the quotient function.

(f⁄g)(x)=  4x + 2

(f⁄g)(-1)=  4(-1) + 2

(f⁄g)(-1)=  -4 + 2

(f⁄g)(-1)=  -2

Thus, the value of (f/g)(x) when x = -1 is -2.

Example 3:

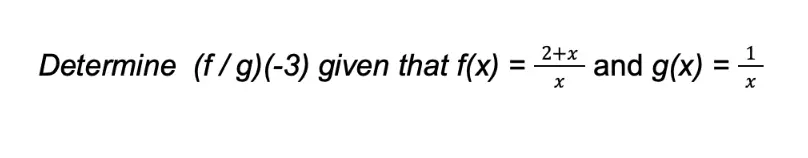
Solution:

To determine (f⁄g)(-3), we have to find out first the quotient function (f⁄g)(x):

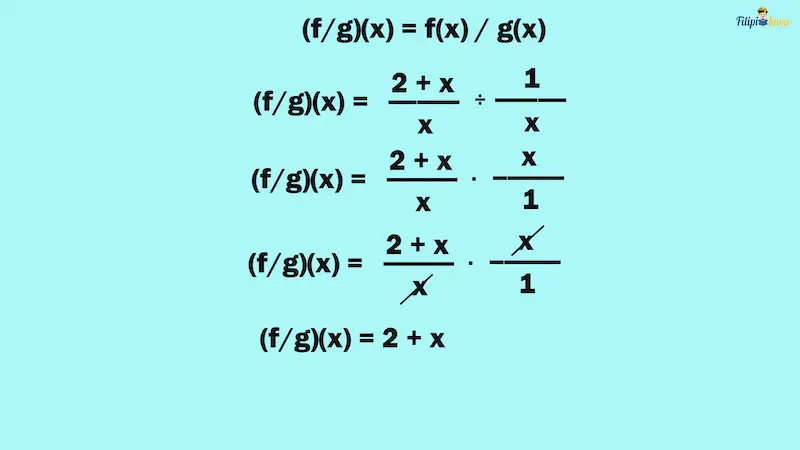
From our computation above, (f⁄g)(x) = 2 + x.

To compute for (f⁄g)(-3), we have to input x = -3 to the quotient function:

(f⁄g)(-3) = 2 + x

(f⁄g)(-3) = 2 + (-3) = -1

The answer is -1.

 

Composition of Functions

Suppose you have an input x and plug it into a certain function g(x). We know that after that, we will obtain an output value g(x). Let’s say we input that output value g(x) to another function, say f(x). After that, we obtain another output value called f(g(x)).

The f(g(x)) is called the composition of the functions f(x) and g(x).

In a composition of functions, an output of a function is the input of another function.

Suppose we have two functions: f(x) = x + 1 and g(x) = 2x.  We want to find the composition of functions f(g(x)).

f(g(x)) means that we input to f(x) the function g(x) itself.

To put it simply, we plug 2x into the independent variable of f(x):

f(x) = x + 1

f(g(x)) = (2x) + 1                  Replace x in f(x) by g(x) = 2x

f(g(x)) = 2x + 1                               

Hence, the composition of functions f(g(x)) is 2x + 1.

Another way to express f(g(x)) is through the symbol (f ∘ g)(x). The hollow dot indicates that g(x) is the input of f(x).

Note that the symbol (f ∘ g)(x) is different from (f ∙ g)(x). (f ∘ g)(x) indicates composition of functions f(x) and g(x). On the other hand, (f ∙ g)(x) indicates the product of the functions f(x) and (gx).

Example 1: If f(x) = 2x – 1 and g(x) = x² + 3. Determine (f ∘ g)(x).

Solution:

The symbol (f ∘ g)(x) tells us that g(x) will be the input of f(x) to obtain the composition or f(g(x)).

(f ∘ g)(x) = f(g(x))

To find f(g(x)):

f(x) = 2x – 1

f(g(x)) = 2(x² + 3) – 1 We input g(x) to f(x)

f(g(x)) = 2x² + 6 – 1

f(g(x)) = 2x² + 5

The answer is f(g(x)) = 2x² + 5

Example 2: If f(x) = 2x – 1 and g(x) = x² + 3. Determine (g ∘ f)(x).

Solution:

The symbol (g ∘ f)(x) tells us that f(x) will be the input of g(x) to obtain the composition or g(f(x)).

(g ∘ f)(x) = g(f(x))

To find g(f(x)):

g(x) = x² + 3

g(f(x)) = (2x – 1)² + 3 We input f(x) to g(x)

g(f(x)) = (4x² – 4x + 1) + 3 Square of binomial

g(f(x)) = 4x² – 4x + 4

Example 3: Using the same functions in the previous example, determine (g ∘ f)(0).

Solution:

The symbol (g ∘ f)(0) tells us that we need to input 0 to the composition of function (g ∘ f) or g(f(x)).

From the previous example, we have obtained (g ∘ f)(x) = g(f(x)) = 4x² – 4x + 4

Let us now determine (g ∘ f)(0):

(g ∘ f)(0) = g(f(0)) = 4(0)² – 4(0) + 4 = 4

Therefore, the answer is 4.

 

Inverse Function

Look at the table of f(x) = x + 4 values. This table is derived by inputting different values of x into the function:

x	0	1	2	3	4	5	6	7
y or f(x)	4	5	6	7	8	9	10	11

Now, what if we reverse the table above? That is, we make x as the y or the f(x), and we also do the same for f(x) and make it as the x of the function (in other words, inputs will be the outputs, outputs will be the inputs).

x	4	5	6	7	8	9	10	11
y or f(x)	0	1	2	3	4	5	6	7

The table above will be the values of the inverse function of f(x) = x + 4.

An inverse function is a function that is formed by interchanging the independent variable and dependent variable of the original function. 

In other words, in an inverse function, the domain of the original function will be the inverse’s range, and the original function’s range will be the inverse’s domain.

If the function is written as a set of ordered pairs, we can easily define its inverse. For instance, the inverse of {(1, 3), (2, 5), (4, 6)} is {(3, 1), (5, 2), (6, 4)}.

If a function is in algebraic form (i.e., in f(x) form), its inverse is expressed as f^-1(x), which is read as “f inverse x.” In the next section, we will discuss how to obtain the inverse of a function.

How To Find the Inverse of a Function

To find the inverse of a function, follow these steps:

1. Write f(x) as y.
2. Interchange x and y in the function.
3. Solve for y in terms of x to solve for the inverse. Write y as f^-1(x) in the final answer.

Example: Determine the inverse of f(x) = 2x – 3.

Solution:

Step 1: Write f(x) as y.

As per instruction, we write f(x) = 2x – 3 as y = 2x – 3.

Step 2: Interchange x and y in the function.

Interchanging x and y in y = 2x – 3 will give us x = 2y – 3.

Step 3: Solve for y in terms of x to solve for the inverse. Write y as f^-1(x) in the final answer,

Solving y in terms of x means that we need to isolate y from other quantities.

 

Types of Functions

In this section, we will talk about six types of functions: identity function, polynomial function, absolute value function, rational function, radical function, and transcendental function.

1. Identity Function

The identity function is one of the most straightforward functions in mathematics. This function is defined as f(x) = x, which means that whatever you input to the function, you will obtain an output equal to that input.

If you input x = 1 to the function, you have f(1) = 1. If you input x = 0.0001, you will obtain f(0.0001) = 0.0001. 

The domain and range of an identity function is the set of all real numbers.

2. Polynomial Function

A polynomial function is a function such that the exponents of its variable are all nonnegative integers. In simple words, this function is expressed in the form of a polynomial.

There are many types of polynomial functions, but we will focus on the two most important ones: the linear and the quadratic functions.

a. Linear Function

A linear function is a polynomial function wherein the largest exponent of the variable is 1. 

For instance, f(x) = 2x + 1 is a linear function since it is polynomial in form and the highest exponent of its variable is 1.

The term “linear” is used for this function since it will be a straight line when you graph it in a coordinate plane.

i. Domain and Range of Linear Functions

The domain and range of a linear function is the set of all real numbers. For instance, the domain and range of f(x) = 2x + 1 are both sets of all real numbers.

ii. Zero of a Linear Function

The zero of a linear function is the value of x such that f(x) = 0. In other words, you should input this to the function so that the output will be 0.

Finding the zero of a linear function is very easy as long as you know how to solve linear equations. To find the zero of a linear function, set f(x) = 0. Then, solve for the value of x.

Example: Find the zero of f(x) = 3x – 6.

Solution:

To find the zero of f(x) = 3x – 6, we set f(x) = 0 then solve for x:

f(x) = 3x – 6

0 = 3x – 6 Set f(x) = 0

-3x = -6 Divide both sides by -3

x = 2

Therefore, the zero of the function f(x) = 3x – 6 is x = 2.

iii. Using Linear Functions to Solve Word Problems

Linear functions are among the most useful functions when solving word problems. In this section, we’ll use this function to solve some problems.

Problem 1: A taxi charges fare in this manner: you must pay a fixed amount of ₱30 and ₱10 for every kilometer you have traveled. How much would you have to pay if you traveled 5 km, 7 km, and 10 km?

Solution:

We can express the situation in the given problem as a linear function.

Let x be the number of kilometers you have traveled.

Then, let 10x represent the amount you must pay for the x kilometer you have traveled.

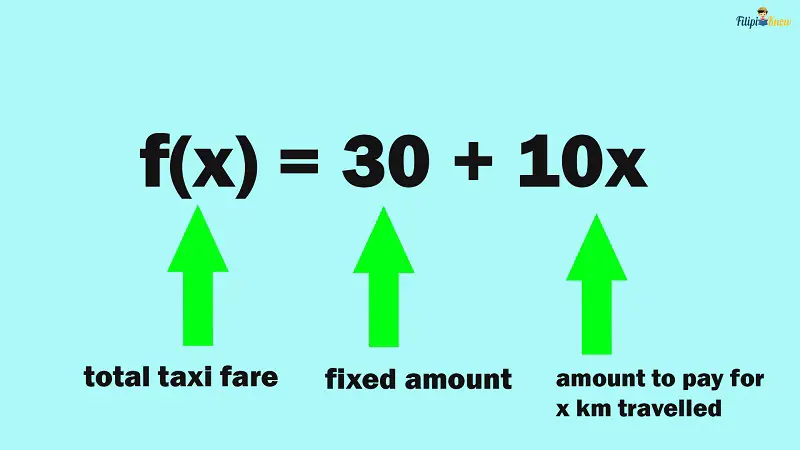
Our linear function is f(x) = 30 + 10x, where f(x) is the amount you must pay after traveling for x kilometers.

If you travel 5 km:

f(x) = 30 + 10x

f(5) = 30 + 10(5)

f(5) = 30 + 50 

f(5) = 80

Hence, you have to pay ₱80 if you travel 5 km.

Can you compute how much you must pay if you travel 7 km or 10 km using the above function?

Problem 2: You plan to buy homemade leche flan from Lena’s Shop. The store charges ₱65 for every order of leche flan and a fixed amount of ₱25 as the service fee. Create a function showing how much you have to pay Lena’s Shop if you plan to buy x orders of leche flan. Determine also how much you will pay if you buy ten orders of leche flan.

Solution:

Let x represent the number of orders of leche flan you’re buying.

This means that 65x represents the amount you must pay for x orders of leche flan you will buy.

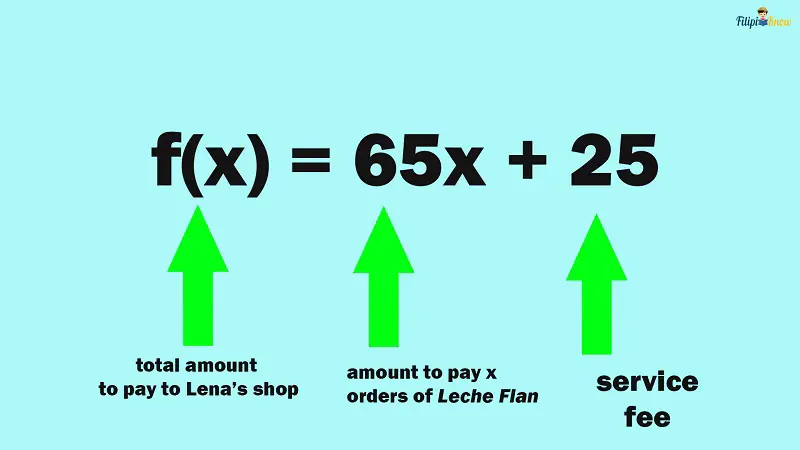
Our linear function is f(x) = 65x + 25, where f(x) represents the total amount you have to pay for x orders of leche flan, including the service fee.

If you buy ten orders of leche flan, that is, x = 10:

f(10) = 65(10) + 25

f(10) = 650 + 25

f(10) = 675

Therefore, you must pay ₱675 for ten orders of leche flan.

b. Quadratic Function

A quadratic function is a polynomial function wherein the largest exponent of its variable is 2. 

For example, f(x) = x² + 3 is a quadratic function since the largest exponent of its variable x is 2. Other examples are f(x) = x² + 2x + 1, f(x) = 3x² – x – 1, and f(x) = 9 – x².

i. Standard Form of a Quadratic Function

The standard form of a quadratic function is f(x) = ax² + bx + c, where a, b, and c are real numbers and a is a nonzero number. 

ax² is called the quadratic term. It is the term in the quadratic function with the quadratic variable or the variable with the exponent of 2. a is the numerical coefficient of the quadratic term.

For example, in f(x) = 3x² + 2x – 1, 3x² is the quadratic term, and a = 3.

bx is called the linear term. It is the term in the quadratic function with the linear variable or the variable with the exponent of 1. b is the numerical coefficient of the linear term.

For example, in f(x) = 3x² + 2x – 1, 2x is the linear term, and b = 2.

c is called the constant term. It is the term in the quadratic function without a variable.

For example, in f(x) = 3x² + 2x – 1, -1 is the constant term so c = -1

Example: Determine the values of a, b, and c (coefficient of each term) of the following:

1. f(x) = x² – 7x + 12
2. f(x) = 9 – x²

Solution:

1. The quadratic term of f(x) = x² – 7x + 12 is x² so a = 1. The linear term is -7x, so b = -7. Lastly, the constant term is 12, so c = 12.
2. The quadratic term of f(x) = 9 – x² is -x² so a = -1. There’s no linear term in f(x) = 9 – x² so b = 0. Lastly, the constant term is 9, so c = 9.

ii. Domain of a Quadratic Function

The domain or the set of all possible values of x is the set of all real numbers. This means that for any real number you input to a quadratic function, you will always obtain an output value or y-value that is a real number.

Example: What is the domain of f(x) = x² – 3x + 1?

Solution:

Since the function is quadratic, its domain is the set of real numbers.

In set notation: D = {x | x  ∈  R}

iii. Range of a Quadratic Function

First, you have to do some calculations to determine the set of all possible y or output values of a quadratic function.

If the coefficient of the quadratic term of the quadratic function (or a) is positive, the range of the quadratic function is R = {y | y ≥ k}.

If the coefficient of the quadratic term of the quadratic function (or a) is negative, the range of the quadratic function is R = {y | y ≤  k}.

The value of k in the expression above is equal to (4ac – b²)/4a  where a, b, and c are the numerical coefficients of the terms of the given quadratic function.

Thus, to find the range of a quadratic function, follow these three steps:

1. Determine the values of a, b, and c.

2. Look at the sign of a first.

• If a > 0, then you will use R = {y | y ≥ k} as the range.
• If a < 0, use R = {y | y ≤ k}.

3. Compute the value of k using the values of a, b, and c.

Note that k = (4ac – b²) / 4a

Example: Determine the range of f(x) = 4x² – 2x + 1.

Solution:

Step 1: Determine the values of a, b, and c.

We have a = 4, b = -2, and c = 1.

Step 2: Look at the sign of a first.

The value of a is 4. This implies that a > 0. Hence, we use R = {y | y ≥ k}.

Step 3: Compute the value of k using the values of a, b, and c.

We compute the value of k using k = (4ac – b²) / 4a.

Again, we have  a = 4, b = -2, and c = 1. Using these values, we obtain the following:

k =  (4ac – b²) / 4a

k = (4(4)(1) – (-2)²) / 4(4)

k = (16 – 4) / 16

k = 12 / 16 or ¾ 

k = ¾

This means that the range of the quadratic function should be R = {y | y ≥ ¾ }

It implies that whatever real number x you input to f(x) = 4x² – 2x + 1, the values of f(x) or y that you will obtain will always be greater than or equal to ¾. It is impossible to have an output value less than ¾ whatever real number x you input.

iv. Zeros of a Quadratic Function

The zeros of a quadratic function are the values of x such that f(x) = 0. In other words, these are the input values of the function that will provide an output value of 0.

Solving for the zeros of a quadratic function is just like solving for a quadratic equation. To find the zeros of a quadratic function, set f(x) = 0. Then, solve for x.

Example: Determine the zeros of the function f(x) = x² – 7x + 12.

Solution: To find the zeros of the given function, we let f(x) = 0 and then solve for x:

f(x) = x² – 7x + 12

0 = x² – 7x + 12

0 = (x – 4)(x – 3) By factoring

x – 4 = 0 x – 3 = 0 Set each factor to 0

x₁ = 4 x₂ = 3

Thus, the zeros of the function  f(x) = x² – 7x + 12 are x = 4 and x = 3.

3. Absolute Value Function

The absolute value function is a function that involves an absolute value sign. Recall that the absolute value of a number is the distance of that number to 0. Since distance is always nonnegative, the absolute value of a number is always nonnegative.

Some examples of this function are f(x) = |x – 2| , f(x) = |x| + 1, f(x) = |x – 3| + 4, and so on.

Example 1: Determine f(-1) if f(x) = |x – 3|

Solution:

f(x) = | x – 3 |

f(-1) = | (-1) – 3 |

f(-1) = | -4| 

f(-1) = 4 Absolute value is always nonnegative

The answer is 4.

Example 2: Compute for f(0) if f(x) = |x – 9| + 7

Solution:

f(x) = |x – 9| + 7

f(0) = |(0) – 9| + 7

f(0) = | – 9 | + 7

f(0) = 9 + 7

f(0) = 16

The answer is 16

Domain and Range of an Absolute Value Function

The domain of an absolute value function is the set of all real numbers.

The range of the absolute value function can be determined this way:

• If the form is f(x) = a|x – h| + k, where k is a real number, then the range will be {y | y < k} if a is negative.
• If the form is f(x) = a|x – h| + k, where k is a real number, then the range will be {y | y > k} if a is positive.

Example 1: What is the domain and range of f(x) = |x – 3|?

Solution:

The domain of f(x) is just the set of all real numbers or D = {x | x ∈ R} 

On the other hand, let us determine the range.

Since the function is in form f(x) = a|x – h| + k, where a is positive and k = 0, then the range is just the set of all nonnegative numbers or R = {y | y  > 0}.

Example 2: What is the domain and range of f(x) = – |x + 1| – 5?

Solution:

The domain of f(x) is just the set of all real numbers or D = {x | x ∈ R} 

Since the function is in form f(x) = a|x – h| + k, where a is negative and k = 0, then the range is the set of all numbers less than or equal to -5 or R = {y | y < -5}.

4. Rational Function

A rational function is a ratio of two polynomial functions. Think of it as a function in a fractional form wherein the numerator and denominator are polynomials.

Example:

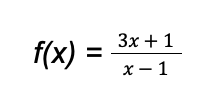
5. Radical Function

From the name itself, a radical function is a function that contains a radical sign. One widely known type of radical function is the square-root function, which involves a square-root sign.

Example:

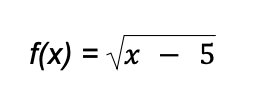
6. Transcendental Function

Transcendental functions include exponential functions, logarithmic functions, and trigonometric functions. Exponential and logarithmic functions are beyond the scope of our reviewer. Meanwhile, we will discuss trigonometric functions in our review of trigonometry.

 

Next topic: Cartesian Coordinate System

Previous topic: Inequalities

Return to the main article: The Ultimate Basic Math Reviewer

 

Download Printable Summary/Review Notes

Download Printable Flashcards

Test Yourself!

1. Practice Questions [PDF Download]

2. Answer Key [PDF Download]

3. Math Mock Exam + Answer Key