You have learned in the previous chapter the basics of trigonometry, specifically the relationship among the angles and sides of a right triangle described using trigonometric functions or ratios.
But we’re merely scratching the surface of trigonometry. Aside from using right triangles, we can also use circles and the cartesian coordinate system to explain the sine, cosine, and tangent functions, as well as their respective reciprocals. This approach to trigonometry is commonly known as “circular trigonometry” or “analytical trigonometry.”
I know that when the words “circular,” “analytical,” and “trigonometry” come together, it doesn’t sound like a piece of cake. We know that it takes a lot of mental power to understand these concepts.
Fret not because, in this reviewer, you will learn circular or analytical trigonometry in a lighter and more friendly way. Read on and explore the other side of trigonometry.
Click below to go to the main reviewers:
Ultimate PMA Entrance Exam Reviewer
Table of Contents
- Degrees and Radians
- Angles in the Coordinate Plane
- The Unit Circle
- Sine and Cosine Functions of a Central Angle
- Sine and Cosine Function Values of Quadrantal Angles in the First Quadrant
- Sine and Cosine Function Values of Special Angles in the First Quadrant
- Summary of Sine and Cosine Function Values of Quadrantal and Special Angles in the First Quadrant
- Reference Angle
- Summary of All Common Angles on the Unit Circle
- Tangent Function of a Central Angle of a Unit Circle
- The Secant, Cosecant, and Cotangent Functions
- Download Article in PDF Format
- Test Yourself!
Degrees and Radians
You learned through our geometry reviewer that an arc is a portion of the circle’s circumference and that an arc of a circle can be measured using the central angle that intercepts it.
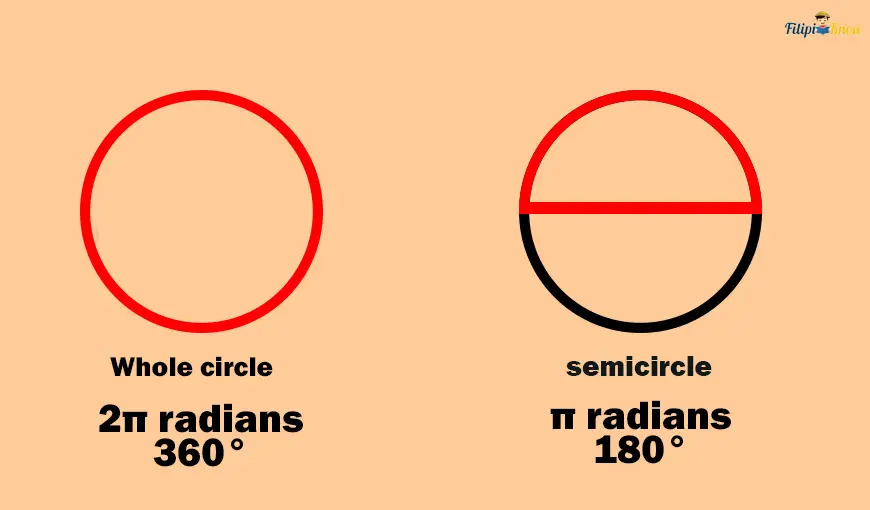
The entire circle has a degree measurement of 360°. Meanwhile, its half (i.e., semicircle) measures 180°.
There’s another way to measure arcs and central angles of a circle aside from using degrees. This is by using “radians.”
A radian is the measure of the arc formed by a central angle whose length is equal to the circle’s radius.
I know that the definition of the radian is quite difficult to grasp, but you will have an idea once you see the figure below.
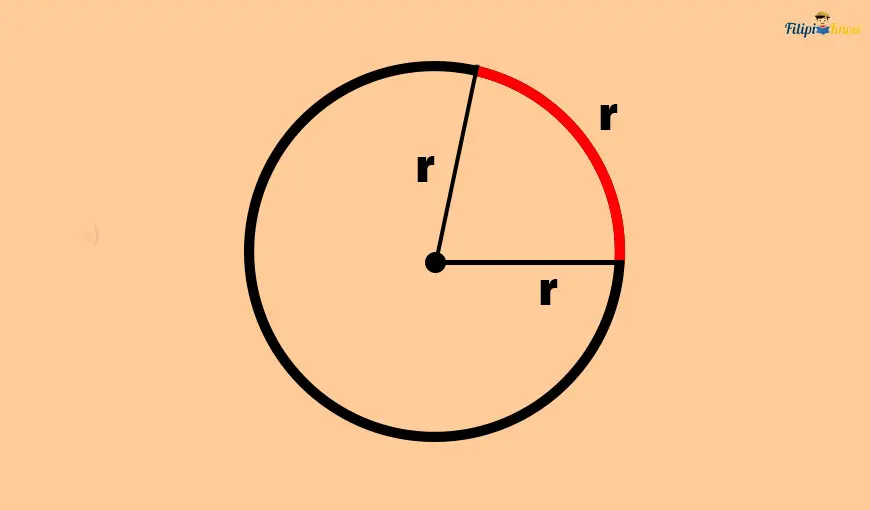
The red arc you see above is formed by the central angle of the circle with the radius of r. The length of this red arc, when you straighten it, will be the same as the length of the circle’s radius.
Keep in mind that in radians, the measurement of the entire circle is 2π.
Since the degree measurement of the entire circle is 360°, we can conclude that 360° = 2π radians.
So, what is 180° in radians?
Since 180° is just half of 360°, then 180° equivalent in radians is
This means that 180° is equal to π radians.
Using the method we have used above, can you determine the equivalent of 30°, 45°, and 90° in radians? Well, we’re going to solve them later as we formally state the steps on how to convert degrees to radians.
But before that, you may have asked yourself this question: Why do we have to use radians to measure arcs and central angles if we already have degrees? Why can’t we just use degrees?
In circular trigonometry, as well as in calculus or physics, the use of radians is preferred as it is easier to use. However, for this reviewer, we will provide the trigonometric function values of central angles, both expressed in degrees and radians.
How To Convert Degrees to Radians
To convert a degree measurement of an arc or a central angle in radians, multiply the given degree measurement by π⁄180.
Sample Problem 1: Convert 360° in radians.
Solution: To convert degrees to radians, all we have to do is to multiply the given degree measurement by π⁄180.
360 × π⁄180 = 360π⁄180 = 2π
Therefore, 360° = 2π radians.
Sample Problem 2: What is 45° in radians?
Solution: To convert degrees to radians, all we have to do is to multiply the given degree measurement by π⁄180.
45 × π⁄180 = 45π⁄180 = π⁄4
Thus, 45° = π⁄4 radians.
How To Convert Radians to Degrees
To convert a radian measurement of an arc or a central angle in a radian, multiply the given degree measurement by 180⁄π and put a degree symbol (°) to the answer.
Sample Problem 1: What are π⁄6 radians in degrees?
Solution: To convert radians to degrees, all we have to do is to multiply the given radian measurement by 180⁄π and put a degree symbol (°) to the answer.
π⁄6 × 180⁄π = 180π/6π = 30°
This means that π⁄6 radians are equivalent to 30°.
Sample Problem 2: What are 3π⁄2 radians in degrees?
Solution: To convert radians to degrees, all we have to do is to multiply the given radian measurement by 180⁄π and put a degree symbol (°) to the answer.
3π⁄2 × 180⁄π = 540π/2π = 270°
This means that 3π⁄2 radians are equivalent to 270°.
Angles in the Coordinate Plane
In trigonometry, we analytically study angles using the coordinate plane.
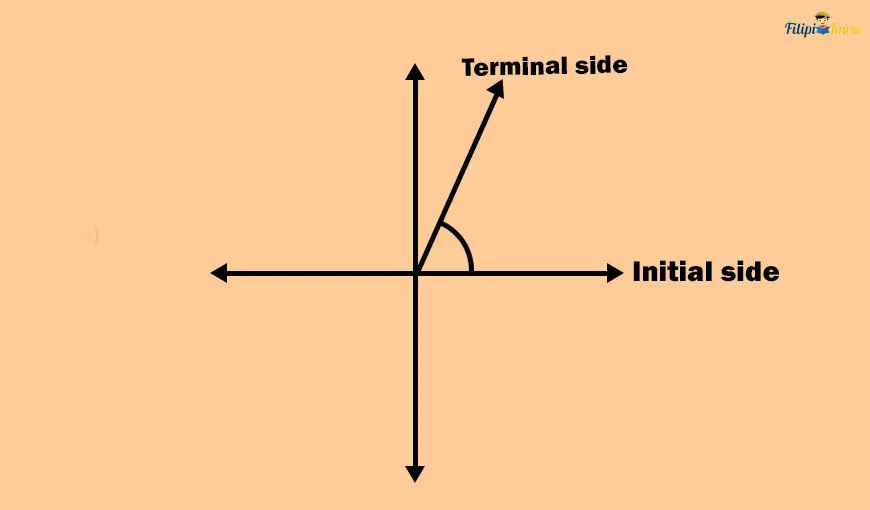
The given angle above is placed in the coordinate plane and has an initial side and a terminal side. If an angle is in standard position, then its initial side is the ray that touches the positive x-axis while the other ray is the terminal side.
The measurement of an angle in the coordinate plane depends on the amount of its rotation from the initial side to the terminal side. In the figure below, the angle rotated 30° from the initial side to the terminal side. Hence, the angle measures 30°. This is equivalent to π⁄6 radians.
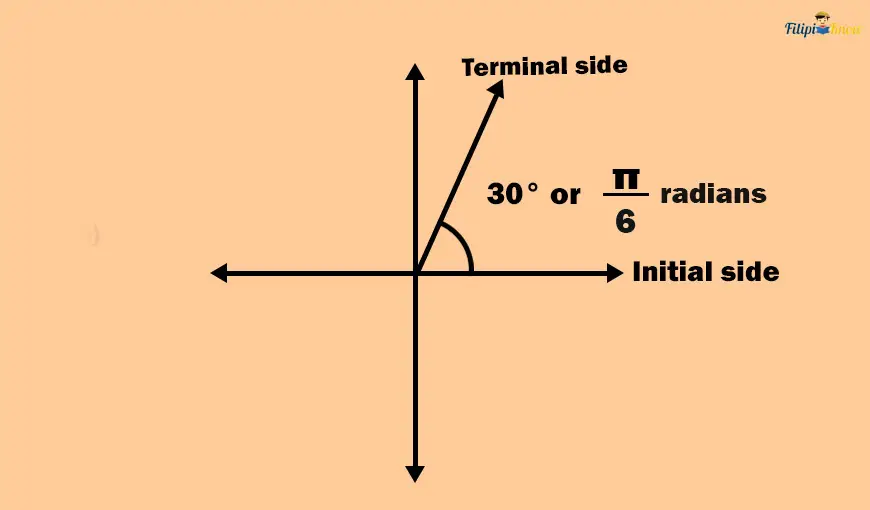
If the rotation is counterclockwise, the measurement of the angle is positive (positive angle). If the rotation is clockwise, the measurement of the angle is negative (negative angle).
In a geometric sense, there’s no “negative” measurement for angles. But, for the sake of precision and convention, we use a negative degree or radian measurement to indicate that the rotation of the angle from the initial side to the terminal side is clockwise.
Sample Problem: Given the measurement of the angle, determine whether the rotation from the initial side to the terminal side is clockwise or counterclockwise.
a. π⁄6 radians
b. -45.45°
c. -π radians
Solution: The given angle measurement in a indicates that the angle’s rotation is counterclockwise since it is positive. On the other hand, both measurements in b and c indicate that the angle’s rotation is clockwise since they are negative.
Using the concept of angle rotation, we can deduce that a circle is equivalent to a one-full 360° (counterclockwise) or -360° (clockwise) rotation of an angle in a standard position. Here, the initial side and the terminal side coincide.
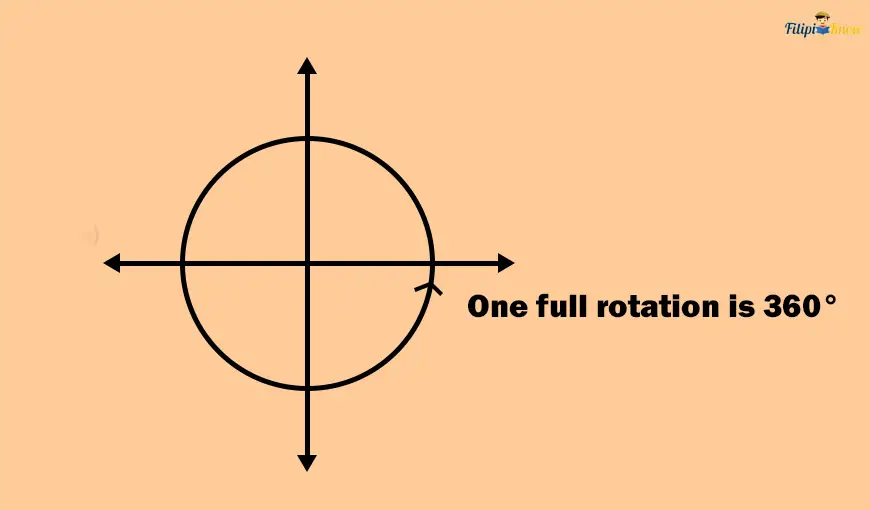
Quadrantal Angles
We also have the so-called quadrantal angles or angles whose terminal side touches the coordinate axes. The quadrantal angles are 0°, 90°, 180°, 270°, and 360°. In radians, the quadrantal angles are 0 radians, π radians, π/2 radians, 3π/2 radians, and 2π radians.
As much as possible, remember how these quadrantal angles look in the coordinate plane. You can refer to the given illustration above.
Coterminal Angles
Most of the time, there are angles in the coordinate plane with different degree measurements (or radian measurements), but if you look at them in the coordinate plane, they look exactly the same.
Look at the angles below with measurements of 135° and -225°. We are sure that these two angles have different measurements, but as you look at them in the coordinate plane, they look exactly the same. What’s going on with these angles?
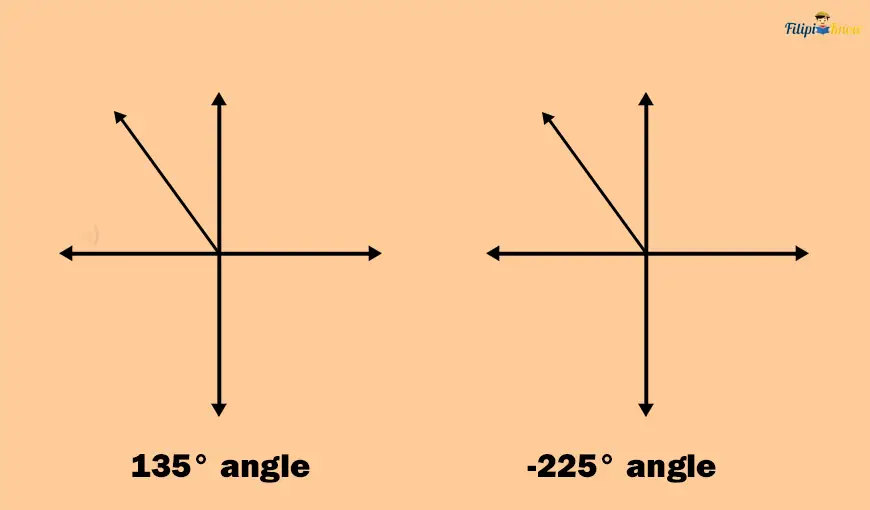
Recall that a 135° angle is formed through a 135° counterclockwise rotation from the initial side to the terminal side. Meanwhile, -225° is formed through a 225° clockwise rotation from the initial side to the terminal side (refer to the figure below for illustration). Since these angles have the same terminal side, they appear exactly the same.
If two angles in the standard position have the same terminal side, then the angles are called coterminal angles. 135° angle and -225° angle are examples of coterminal angles.
Finding a Coterminal Angle to a Given Angle With Measurement Greater Than 360° or 2π Radians
We can determine a coterminal angle to a certain angle whose measure is beyond 360° (or 2π radians) using the steps indicated below.
- If the given angle is in radians, convert it to degrees. Otherwise, proceed to step 2.
- Subtract 360° from the given angle. If the result is already less than 360°, stop. The result is the coterminal angle of the given angle. If the result is still greater than 360°, proceed to step 3.
- Subtract 360° from the resulting number you have obtained from Step 2. Continue this process until you obtain a number that is between 0° to 360°. Once you have obtained a number between 0 to 360, that angle is the one we are looking for.
- If necessary, convert the calculated degree measurement to radians.
Sample Problem 1: Determine the measurement of the coterminal angle θ of 540° such that the measurement of θ is between 0° and 360°.
Solution:
Step 1: If the given angle is in radians, convert it to degrees. Otherwise, proceed to step 2.
The given angle is already in degrees, so we can skip this step.
Step 2: Subtract 360° from the given angle. If the result is already less than 360°, stop. The result is the coterminal angle of the given angle. If the result is still greater than 360°, proceed to step 3.
540° – 360° = 180°
We already obtained a number less than 360°, so we stop here. We don’t have to perform steps 3 and 4, so the coterminal angle of 540° is 180°.
Let us verify whether 180° and 540° are coterminal angles or not by graphing them in the coordinate plane.
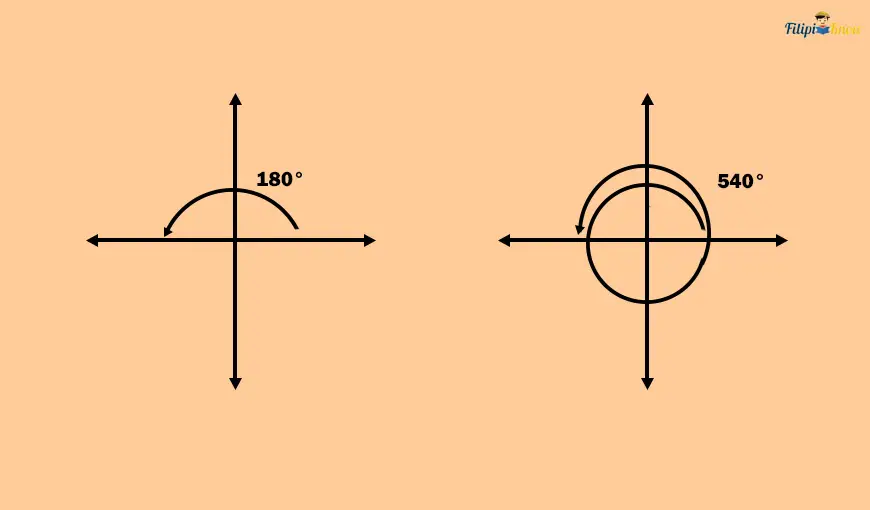
The angles have the same terminal side; indeed, the angles are coterminal angles.
Sample Problem 2: Determine the largest possible measurement of a coterminal angle of 920° such that 0° < θ < 360°.
Solution:
Step 1: If the given angle is in radians, convert it to degrees. Otherwise, proceed to step 2.
The given angle is already in degrees, so we can skip this step.
Step 2: Subtract 360° from the given angle. If the result is already less than 360°, stop. The result is the coterminal angle of the given angle. If the result is still greater than 360°, proceed to step 3.
920° – 360° = 560°
The resulting number is greater than 360°, so we must proceed to step 3.
Step 3: Subtract 360° from the resulting number you have obtained from Step 2. Continue this process until you obtain a number that is between 0° to 360°. Once you have obtained a number between 0 to 360, that angle is the one we are looking for.
The number we have obtained from step 2 is 560°. As per step 3, let us subtract 360 from it:
560° – 360° = 200°
The resulting measurement, which is 200°, is already less than 360°. Therefore, the coterminal angle of 920° we are looking for is 200°.
Step 4: If necessary, convert the calculated degree measurement to radians.
Since the given angle is 920°, there’s no need to convert 200° in radians. Hence, the answer for this example is 200°.
Sample Problem 3: Determine a positive coterminal angle of 3π radians less than 360°.
Solution:
Step 1: If the given angle is in radians, convert it to degrees. Otherwise, proceed to step 2.
The given angle is 3π, which is in radians, so let us convert it to degrees by multiplying it by 180⁄π:
3π × 180⁄π = 540π⁄π = 540
Thus, 3π radians = 540°.
Since we already converted the given angle in radians into degrees, we can proceed to step 2.
Step 2: Subtract 360° from the given angle. If the result is already less than 360°, stop. The result is the coterminal angle of the given angle. If the result is still greater than 360°, proceed to step 3.
The given angle is 3π radians which is equal to 540°.
We subtract 360° from 540°:
540° – 360° = 180°
Since we have obtained a degree measurement of less than 360°, we don’t have to proceed to step 3. The coterminal angle we are looking for is 180°. However, since the given angle in this problem is in radians, we must convert 180° to radians, so we jump into step 4.
Step 3: We skip this step.
Step 4: If necessary, convert the calculated degree measurement to radians.
To convert 180° to radians, we just multiply it by π⁄180:
180 × π⁄180 = π
Hence, the answer is radians.
Finding a Coterminal Angle to a Given Angle With a Measurement Less Than 0°
Recall that if an angle has a negative degree measurement, it means a clockwise rotation from its initial side to its terminal side. We can determine a positive angle (or an angle rotated in a counterclockwise rotation) that is coterminal with a negative angle.
Here are the steps:
- If the given angle is in radians, convert it to degrees.
- Add 360° to the given angle. If the result is still negative, proceed to step 3. Otherwise, the resulting measurement is the coterminal angle.
- Add 360° to the result you have obtained in step 2. Continue this process until you obtain a positive angle. Once you have obtained one, the result is the coterminal angle.
- If necessary, convert the resulting degree angle measurement to radians.
Sample Problem 1: Determine the smallest positive angle less than 360°, which is a coterminal angle of -30°.
Solution:
Step 1: If the given angle is in radians, convert it to degrees.
The given angle is already in degrees and not in radians, so we can skip this step.
Step 2: Add 360° to the given angle. f the result is still negative, proceed to step 3. Otherwise, the resulting measurement is the coterminal angle.
-30° + 360° = 330°
We have already obtained a positive angle measurement, so no need to proceed to step 3. Hence, the coterminal angle is 330°.
Sample Problem 2: Determine the smallest positive angle less than 360°, which is a coterminal angle of -520°.
Solution:
Step 1: If the given angle is in radians, convert it to degrees.
The given angle is already in degrees and not in radians, so we skip this step.
Step 2: Add 360° to the given angle. If the result is still negative, proceed to step 3. Otherwise, the resulting measurement is the coterminal angle.
-520° + 360° = -160°
The degree measurement we obtained is still negative, so let us proceed to the third step.
Step 3: Add 360° to the result you have obtained in step 2. Continue this process until you obtain a positive angle. Once you have obtained one, the result is the coterminal angle.
-160° + 360° = 200°
We have already obtained a positive degree measurement which is 200°, so this is the coterminal angle we are looking for.
Step 4: If necessary, convert the resulting degree angle measurement to radians.
No need to convert to radians since the given angle is in degrees.
Thus, the answer to this example is 200°.
Sample Problem 3: Determine the smallest positive coterminal angle less than 2π radians of the angle – π radians.
Solution:
Step 1: If the given angle is in radians, convert it to degrees.
The given angle has a measurement of – π radians. Thus, we need to convert it first to degrees.
To convert radians to degrees, we need to multiply the given radian measurement by 180⁄π:
-π × 180⁄π = -180°
Thus, the equivalent of – π radians in degrees is -180°.
Step 2: Add 360° to the given angle. If the result is still negative, proceed to step 3. Otherwise, the resulting measurement is the coterminal angle.
-180° + 360° = 180°
We have obtained a positive angle measurement. So, no need to proceed to the third step. The coterminal angle measures 180°.
However, we must express 180° to radians. We do this by multiplying it by π⁄180:
180 × π⁄180 = π
Thus, the answer for this example is π radians.
Using the concepts of degrees, radians, and angles in the coordinate plane, you’re ready to proceed to the highlight of this reviewer – the unit circle. Make sure that you already have a good grasp of the concepts above because they are important as you explore the intricacy of the unit circle.
The Unit Circle
The unit circle is a circle with a radius of 1 unit that is graphed in the cartesian coordinate system.
As you can see below, the center of the unit circle is the origin (0, 0), and it touches the points (1,0), (0, 1), (-1, 0), and (0, -1), implying that the circle has a radius of 1 unit.
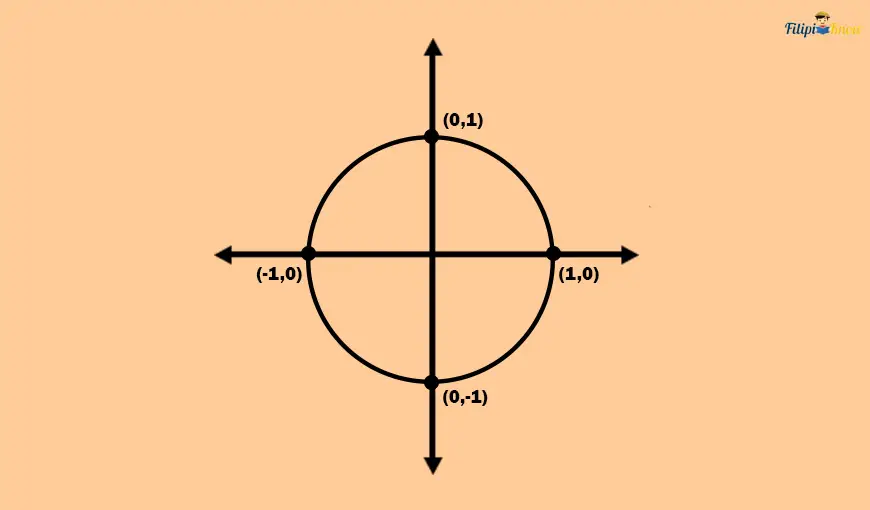
Let’s say there’s a unit circle with a central angle θ. The initial side of θ is the positive x-axis, while its terminal side is the radius of the circle. The endpoints of the terminal side are the origin and a point on the unit circle, which we label as (x, y).
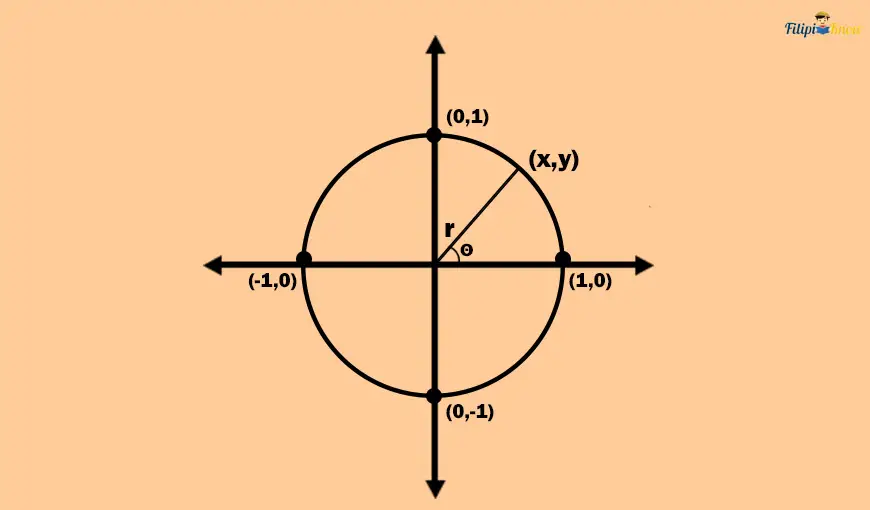
This point (x, y) will be the one that will define the values of the trigonometric functions of θ.
Sine and Cosine Functions of a Central Angle
As shown in our previous image, we have a central angle of the unit circle that is in standard position with its terminal side touching the point (x, y) on the unit circle.
Suppose that we draw a right triangle using the illustration above, where the legs are the horizontal distance from the origin to x, the vertical distance from the origin to y, and the hypotenuse is the circle’s radius which is also the terminal side of θ.
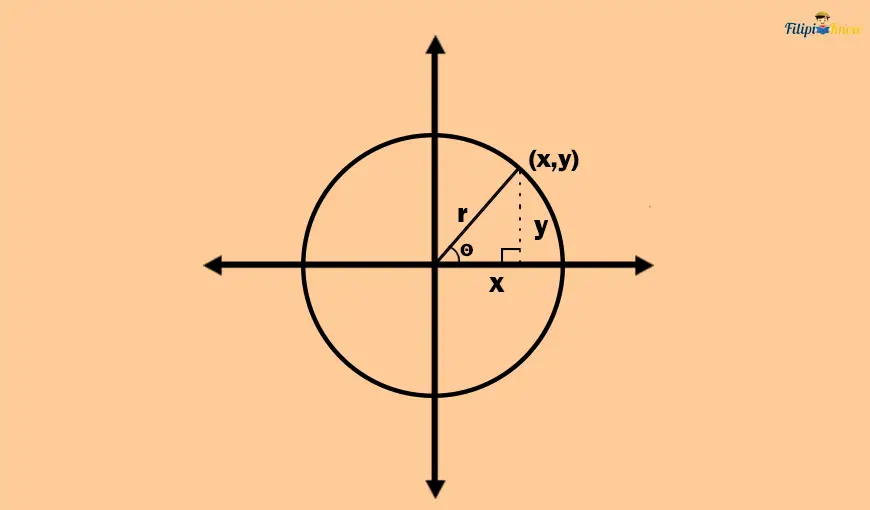
Now, let us define the sine of the central angle θ. If you may recall, the sine function of an angle is the ratio of the length of the opposite side of the angle to the length of the hypotenuse:
Sin θ = opposite side/hypotenuse
In the figure above, the measurement of the opposite side of the central angle is the vertical distance y. Meanwhile, the hypotenuse is the radius with a length of 1.
Sin θ = y/1 = y
This means that the sine function of the central angle θ is just the y-coordinate of the endpoint (x, y) of the terminal side.
Meanwhile, the cosine of an angle is the ratio of the length of the adjacent side of the angle to the length of the hypotenuse:
Cos θ = adjacent side/hypotenuse
In the figure above, the measurement of the adjacent side of the central angle is the horizontal distance x. Meanwhile, the hypotenuse is the radius with a length of 1.
Cos θ = x⁄1 = x
This means that the cosine function of the central angle θ is just the x-coordinate of the endpoint (x, y) of the terminal side.
To summarize: If a central angle θ has a terminal side with endpoints (0, 0) and (x, y), the sine and cosine functions of the central angle θ are defined as
sin θ = y
cos θ = x
If the given angle is a quadrantal angle, we can identify its sine and cosine function values since we can easily determine what point on the unit circle its terminal side coincides with.
Sine and Cosine Function Values of Quadrantal Angles in the First Quadrant
We will derive the sine and cosine function values of quadrantal angles in the first quadrant of the cartesian coordinate plane. These angles are the 0° and the 90° (π⁄2 radians). The sine and cosine function values of these angles are easy to derive, so we will start our derivation with them.
Sample Problem 1: Determine the values of the sine and cosine functions of 0°.
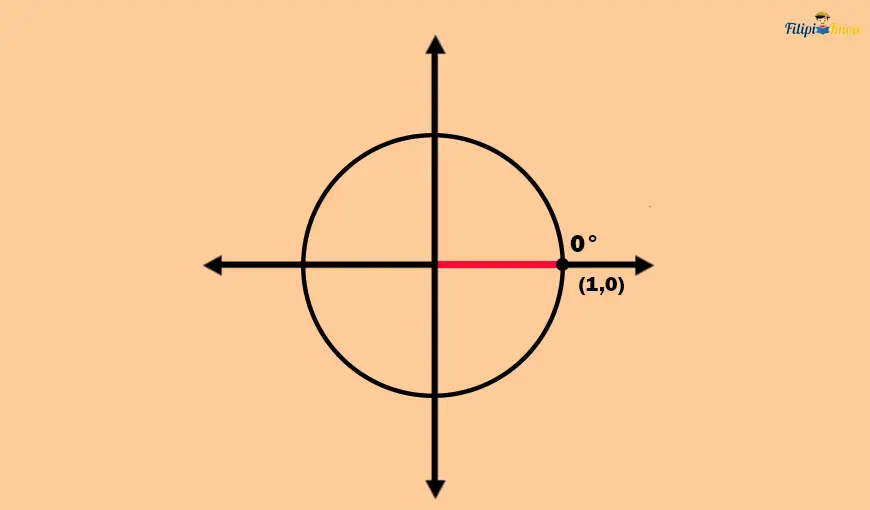
Solution: 0° has the x-axis as its initial and terminal sides. Thus, the point that the terminal side touches in the unit circle is (1,0).
The sine function is just the y-coordinate of (1, 0). Thus, sin(0°) = 0.
Meanwhile, the cosine function is just the x-coordinate of (1, 0) which is 1. Thus, cos(0°) = 1.
Sample Problem 2: Determine the values of the sine and cosine functions of the 90° ( π⁄2 radians).
Solution: The 90° angle is a quadrantal angle with the positive y-axis as its terminal side.
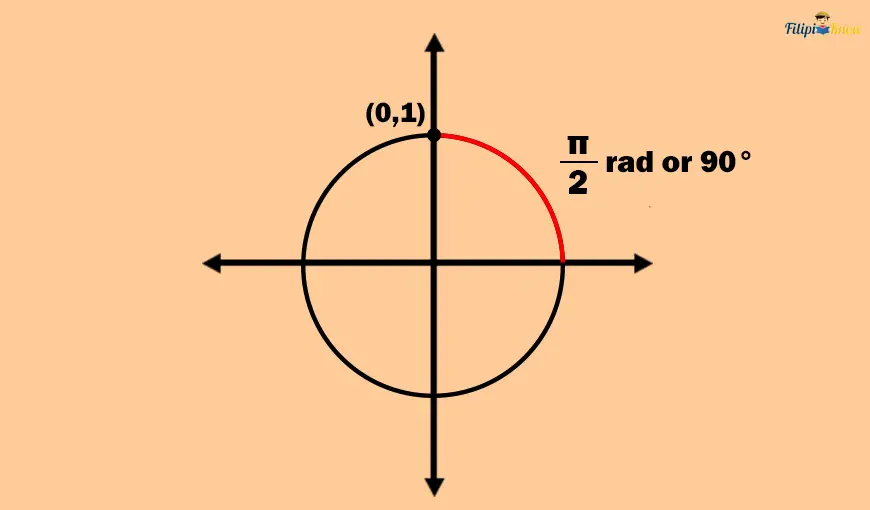
As you can see in the image above, the 90° angle has a terminal side that touches the point (0, 1) on the unit circle.
Thus, the sine function of 90° is just the y-coordinate of (0, 1) which is 1. Thus, sin(90°) = 1
Meanwhile, the cosine function of 90° is just the x-coordinate of (0, 1) which is 0. Thus, cos(90°) = 0
This also means that sin(π⁄2) = 1 while cos(π⁄2) = 0.
As you can see from our examples above, it’s pretty quick and easy to find the sine and cosine function values of quadrantal angles with terminal sides located in the first quadrant (0° and 90°).
In our next section, we are going to learn how to determine the sine and cosine function values of special angles – 30°, 45°, and 60° with terminal sides that are also located in the first quadrant. Do you still remember these special angles we discussed in the previous reviewer?
Sine and Cosine Function Values of Special Angles in the First Quadrant
1. How To Find the Sine and Cosine Function Values of 45°
Let’s look at the 45° angle in the coordinate plane in the image below.
As you can see, 45° is not a quadrantal angle since its terminal side does not touch any of the coordinate axes. For this reason, it is not that straightforward to determine its sine and cosine function values.
Let (x, y) be the point where the terminal side of 45° touches the unit circle. Once we have determined what x and y stand for (x, y), we can determine the sine and cosine function values of 45°. But the question is, How do we determine (x, y)?
Let’s go back to the illustration of the 45° angle in the unit circle above. Using this same illustration, we create a right triangle with the horizontal distance from the origin to x and the vertical distance from the origin to y as legs. Meanwhile, the hypotenuse of this right triangle is one of the circle’s radii. As you can see, the 45° angle is one of the right triangle’s interior angles.
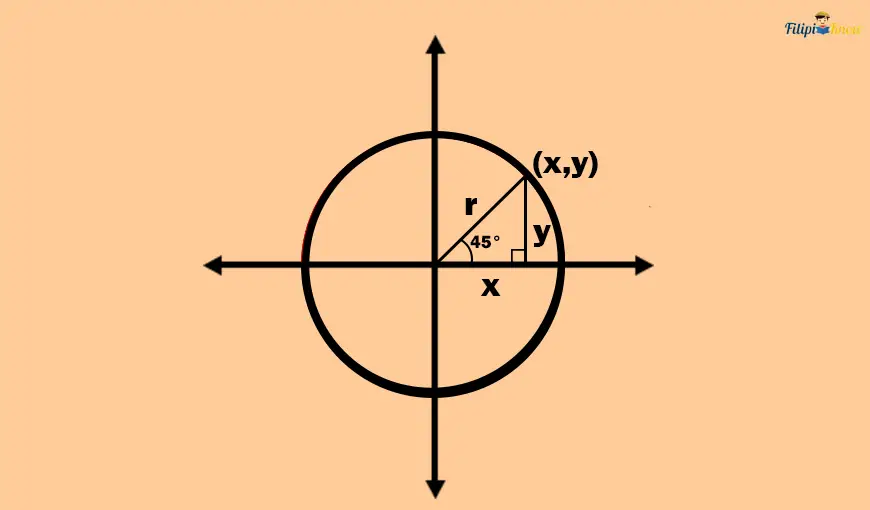
As you can see above, we have formed a 45° – 45° – 90° right triangle or an isosceles right triangle (since we have one 45° angle). This means that the legs of the right triangle above are congruent or equal (recall the definition of an isosceles right triangle). Since x and y represent the length of the legs of the right triangle above, then we expect that the values of x and y are the same in (x, y).
Meanwhile, the radius of the unit circle is always 1 unit. Therefore, the hypotenuse of the isosceles right triangle we have formed is 1 unit long.
According to the isosceles right triangle theorem, the hypotenuse of an isosceles right triangle is √2 times longer than the legs. If the hypotenuse of our isosceles right triangle is 1 unit long, then it follows that the length of the legs x and y is √2/2 units (Solution is shown below)
Hypotenuse = √2(leg)
1 = √2 (leg) Our hypotenuse is 1 unit long
1/√2 = √2 (leg) / √2 Dividing both sides by 2
Leg = 1/√2 or √2/2
This means that x and y, representing the length of the legs of our isosceles right triangle, are equal to √2/2 units.
Thus, the point (x, y) is actually (√2/2, √2/2). This means that the terminal side of the 45° angle touches the point (√2/2, √2/2).
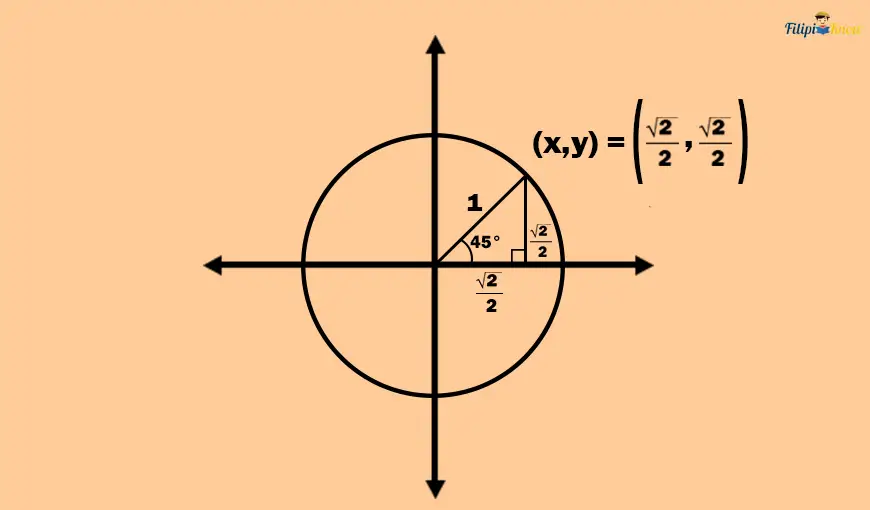
We can now identify the sine and cosine function values of 45°.
The sine of 45° is just the y-coordinate of (√2/2, √2/2). Therefore, sin(45°) = √2/2.
The cosine of 45° is just the x-coordinate of (√2/2, √2/2). Therefore, cos(45°) = √2/2.
As you can see, the sine and cosine function values of 45° are equal.
The sine of π⁄4 radians is just the y-coordinate of (√2/2, √2/2). Therefore, sin(π⁄4) = √2/2.
The cosine of π⁄4 radians is just the x-coordinate of (√2/2, √2/2). Therefore, cos(π⁄4) = √2/2.
2. How To Find the Sine and Cosine Function Values of 30° and 60°
a. Sine and Cosine Function Values of the 30° Angle
Let us start with the 30° angle. We create a right triangle containing the central 30° angle of the unit circle, making it an interior angle. If one of the interior angles of a right triangle is 30°, it follows that the remaining interior angles are 60° and 90°. Hence, we have formed a 30°– 60°– 90° right triangle.
Let (x, y) be the point intercepted by the terminal side of the 30° angle in the unit circle. We will define the sine and cosine function values of the 30° angle using the values of x and y (x, y). But how do we determine (x, y)?
As you can see above, x and y represent the longer and the shorter legs of the 30°– 60°– 90° right triangle, respectively, while the hypotenuse is the radius of the circle. Since the radius of a unit circle is always 1 unit, then the hypotenuse of the 30°– 60°– 90° right triangle above measures 1 unit.
According to the 30° – 60° – 90° right triangle theorem, the hypotenuse of a 30° – 60° – 90° right triangle is twice as long as the shorter leg. Hence, if the hypotenuse of our 30°– 60°– 90° right triangle is 1 unit long, it means that the shorter leg is ½ unit long. Since y represents the length of the shorter leg, this means that y = ½.
On the other hand, the longer leg of a 30° – 60° – 90° right triangle is √3 times as long as the shorter leg. We have already discovered that the shorter leg is ½ unit long. So, the longer leg must be √3 x ½ long or √3/2 units long. Since x represents the length of the longer leg, it means that x = √3/2.
The previous analysis took a lot of brute force, so let’s just summarize our derivations in the image below:
As you can see, the point intercepted by the terminal side of the 30° angle in the unit circle is the point (√3/2, 1⁄2).
We can now identify the sine and cosine function values of 30°.
The value of the sine of 30° is just the y-coordinate of (√3/2, 1⁄2) which is ½. This means that sin(30°) = ½.
For the cosine function, since the x-coordinate of (√3/2, 1⁄2) is √3/2. Then, cos(30°) = √3/2.
If you can still remember, the 30° angle is equal to π⁄6 radians. Since we have already computed above that sin(30°) = ½ and cos(30°) = √3/2, then:
sin(π⁄6) = ½ and cos(π⁄6) = √3/2
b. Sine and Cosine Function Values of the 60° Angle
Deriving the sine and cosine function values of the 60° angle is very similar to how we derive the sine and cosine values of the 30° angle. We draw a right triangle with an interior angle of 60° and form a 30° – 60° – 90° right angle. We label the point intercepted by the 60° angle’s terminal side as (x, y).
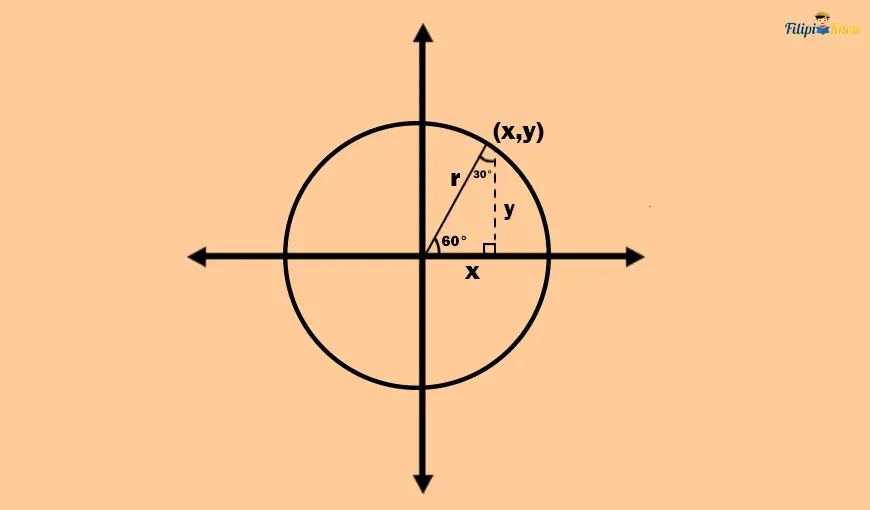
As you can see, x represents the length of the shorter leg of the 30° – 60° – 90° right angle, while y represents the longer leg. As always, the hypotenuse is still one of the circle’s radii which is 1 unit long.
We will not elaborate further on how the values of x and y were derived since the process is the same as our derivation for the 30° angle. Again, we have just applied the 30° – 60° – 90° right angle theorem. We will obtain that the shorter leg is ½ unit long while the longer leg is √3/2 units long. Since x and y represent the measurements of the shorter and longer legs, respectively, then x = ½ and y = √3/2.
Thus, the coordinate intercepted by the terminal side of the 60° angle in the unit circle is the point (½, √3/2).
The value of the sine of 60° is just the y-coordinate of (½, √3/2) which is √3/2. This means that sin(60°) = √3/2.
On the other hand, the cosine of 60° is just the x-coordinate of (½, √3/2). which is ½. This means that cos(60°) = 1⁄2.
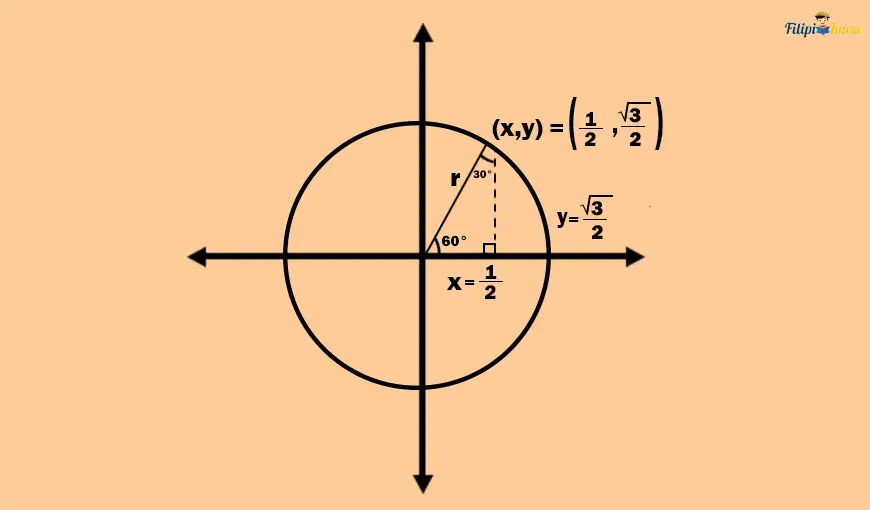
60° is equivalent to π⁄3 radians. Since sin(60°) = √3/2 and cos(60°) = ½ . Then, it means that: sin(π⁄3) = √3/2 and cos(π⁄3) = ½.
Summary of Sine and Cosine Function Values of Quadrantal and Special Angles in the First Quadrant
We can now summarize the sine and cosine function values of quadrantal and special angles in the first quadrant since we have already derived them in the previous sections. These angles are the 0°, 30°, 45°, 60°, and 90° angles.
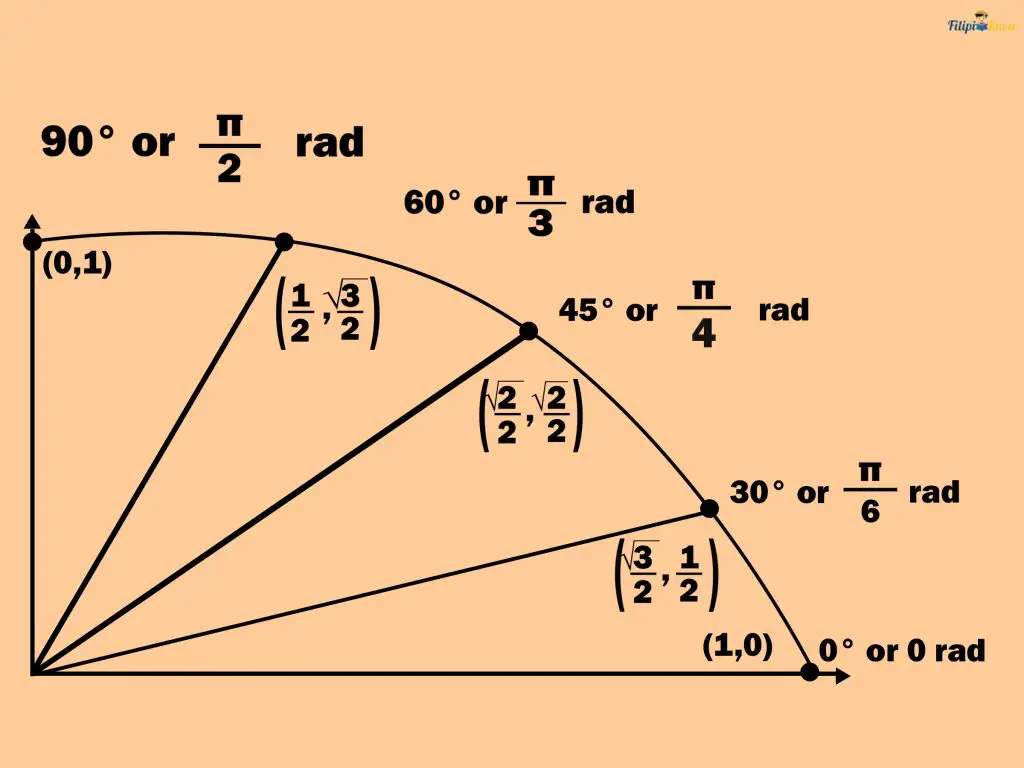
| Angle | Sine | Cosine |
| 0° | 0 | 1 |
| 30° or π⁄6 rad | ½ | √3/2 |
| 45° or π⁄4 rad | √2/2 | √2/2 |
| 60° or π⁄3 rad | √3/2 | ½ |
| 90° or π⁄2 rad | 1 | 0 |
Now that we have already figured out the sine and cosine function values of quadrantal and special angles in the first quadrant, our next goal is to identify the values for those angles in the second to the fourth quadrant of the coordinate plane. However, deriving those angles is not that straightforward unlike the angles above.
In the succeeding sections, you’ll learn how to derive the sine and cosine function values of quadrantal and special angles in the 2nd to the 4th quadrant using reference angles.
Reference Angle
Consider the central angle below which measures 135°. Notice that the terminal side of this angle is already located in the second quadrant. If we want to derive the sine and cosine function values of 135°, it will not be that straightforward since 135° is not located in the first quadrant.
What should we do?
We need to determine a reference angle for 135°.
The reference angle is the smallest angle that the terminal side of the given angle makes with the x-axis. This definition sounds confusing, but it only implies the shortest-degree measurement of the terminal side from the x-axis.
Take a look at the 135° angle again. Notice that the terminal side of this angle is nearer to the negative x-axis than the positive x-axis.
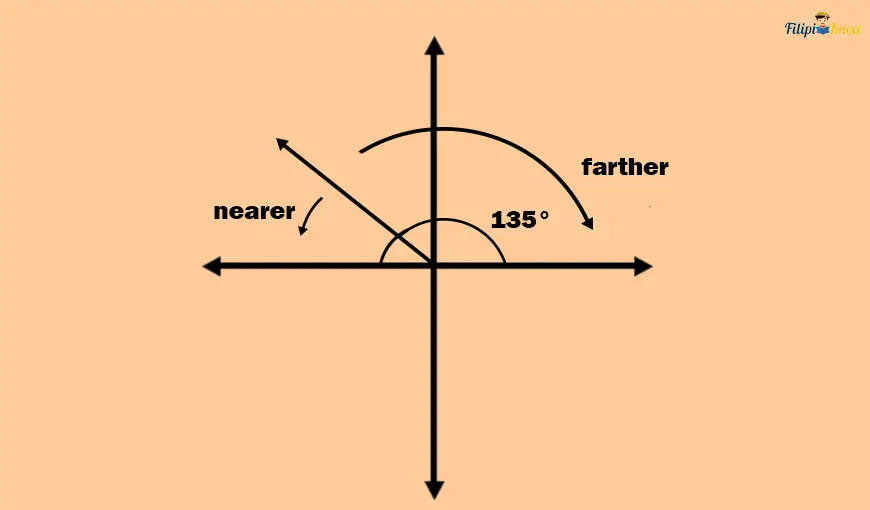
Hence, we need to determine the degree measurement of the angle created between the terminal side and the negative x-axis. This degree measurement is the reference angle.
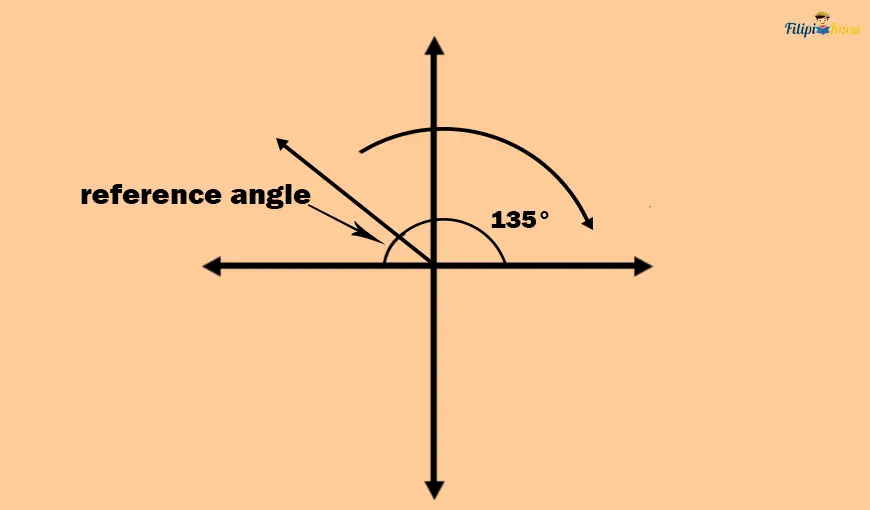
Since the entire angle formed from the positive x-axis to the negative x-axis measures 180°, then the reference angle should be 180° – 135° = 45°.
Thus, the reference angle of 135° is 45°.
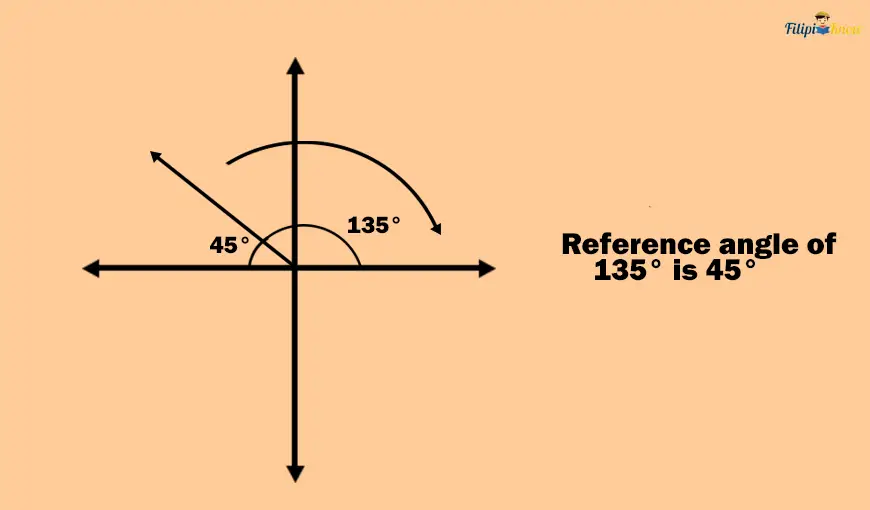
There’s an easier way to find the reference angle of a given central angle, and that is by doing some calculations. To find the reference angle of a given angle, remember the following:
- If the angle is in the first quadrant, the angle itself is the reference angle.
- If the angle is in the second or third quadrant, then the reference angle is the absolute value of the difference between 180° and the measurement of the given angle or |180° – t| where t is the given angle measurement.
- If the angle is in the fourth quadrant, then the reference angle is the absolute value of the difference between 360° and the measurement of the given angle or |360° – t| where t is the measurement of the given angle.
- If the angle has a negative measurement or has a measurement of more than 360°, then the reference angle can be obtained by adding 360° (to the negative angle) until you obtain the positive equivalent angle or by subtracting 360° (to the angle that is more than 360°) to obtain an equivalent angle less than 360°.
I know the techniques above are mind-boggling, but it’s the fastest way to find the reference angle. If you prefer an illustration like what we’ve used for 135°, you can also do that. However, for the rest of this reviewer, we will be using the techniques above to compute the reference angle.
Sample Problem: Determine the reference angle of the following:
- 120°
- 150°
Solution: Since 120° and 150° are both in the second quadrant, all we need to do is to subtract them both from 180°:
180° – 120° = 60°
180° – 150° = 30°
Hence, the reference angles of 120° and 150° are 60° and 30°, respectively.
Determining Sine and Cosine Function Values Using the Reference Angle
Here’s an important thing you need to keep in mind about a given angle and its reference angle: The sine and cosine function values of a given angle is equal to the sine and cosine function values of its reference angle except for the signs.
Let us illustrate this property in our example below.
Suppose we want to determine the sine and cosine function values of 135°. Again, this angle (or its terminal side) is located in the second quadrant, so we cannot quickly identify the coordinates which enable us to determine its sine and cosine function values.
We have shown earlier that 45° is the reference angle of 135°. This means that the sine and cosine function values of 135° are equal to the sine and cosine function values of 45° except for the signs.
Recall that the sin(45°) = √2/2 while cos(45°) = √2/2. These will also be the values of sine and cosine of 135°. But we are not done yet; we need to consider the signs of these values as well.
Since 135° is located in the second quadrant, where x-coordinates are negative but y-coordinates are positive, the sine of 135° should be positive, and its cosine must be negative.
Therefore, the sin(135°) = √2/2 and cos(135°) = – √2/2.
This also implies that the 135° angle touches the point (-√2/2, √2/2) on the unit circle.
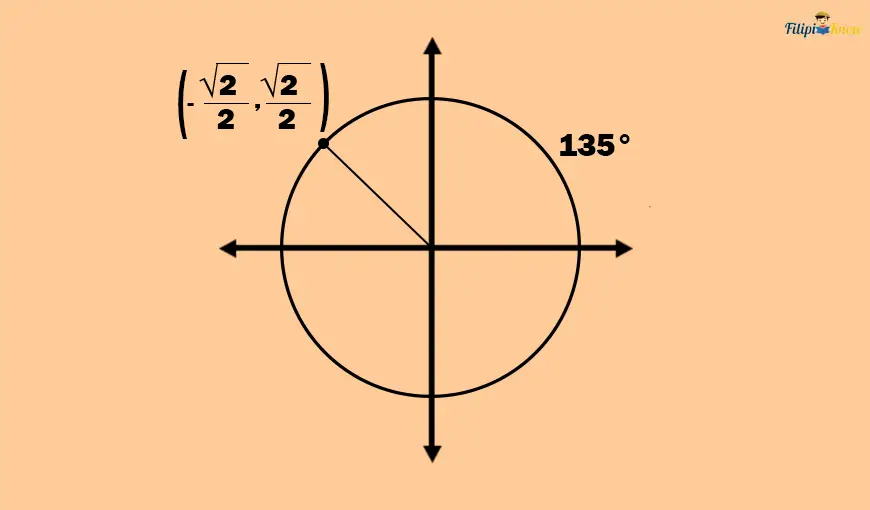
From our previous calculation, it seems that 135° is the “counterpart” of 45° in the second quadrant.
Sample Problem 1: Determine the coordinates of the point on the unit circle at an angle of 120° or 2π⁄3 radians and its sine and cosine function values.
Solution:
The reference angle of 120° is 180° – 120° = 60°.
Hence, 120° is the “counterpart” of 60° in the second quadrant.
If you can still remember, the coordinates of the point on the unit circle at an angle of 60° is (1⁄2, √3/2).
This means that these are also the coordinates of the point on the unit circle at an angle of 120°, but there are differences in the signs of the coordinates.
120° is located in the second quadrant with x-coordinates negative and y-coordinates positive. This means that the coordinate of 120° must have a negative x-coordinate and a positive y-coordinate. Thus, 120° intercepts the point (- 1⁄2, √3/2) on the unit circle.
It follows that sin(120°) = √3/2 while cos(120°) = – 1⁄2.
This also means that sin(2π⁄3) = √3/2 and cos(2π⁄3) = – ½.
Sample Problem 2: Determine the coordinates of the point on the unit circle at an angle of 240° or 43 radians and its sine and cosine function values.
Solution: 240° is located in the third quadrant. So, we need a reference angle to identify the coordinate it intercepted on the unit circle and its sine and cosine values.
Computing for its reference angle: |180° – 240°| = |-60°| = 60°
Thus, the reference angle of 240° is 60°.
This means that the coordinate of 240° is the “counterpart” of 60° in the third quadrant.
If you can still remember, the coordinates of the point on the unit circle at an angle of 60° are (12, 32).
This means that this point should be the one intercepted by 240° but with different signs.
240° is in the third quadrant with x-coordinates negative and y-coordinates negative. This implies that 240° has a point with both a negative x-coordinate and y-coordinate.
Thus, 240° touches the point (-12, -32) on the unit circle.
It follows that sin(240°) = -32 while cos(240°) = -½ .
This also means that sin(4π⁄3) = -32 while cos(4π⁄3) = -½ .
Using the reference angle, we can derive the point that an angle touches on the unit circle and its respective sine and cosine values. This means that we can also derive the sine and cosine function values of the “counterparts” of 0°, 30°, 45°, 60°, and 90° angles in the second to the fourth quadrant. However, we will not derive them one by one (since there are too many) and instead just present them in the next section.
Summary of All Common Angles on the Unit Circle
Shown in the image below is the coordinates of the “counterparts” of 0°, 30°, 45°, 60°, and 90° throughout the unit circle. We call the collection of the quadrantal and special angles and their counterparts in the second to the fourth quadrant as common angles. Note that the coordinates were derived using their respective reference angles.
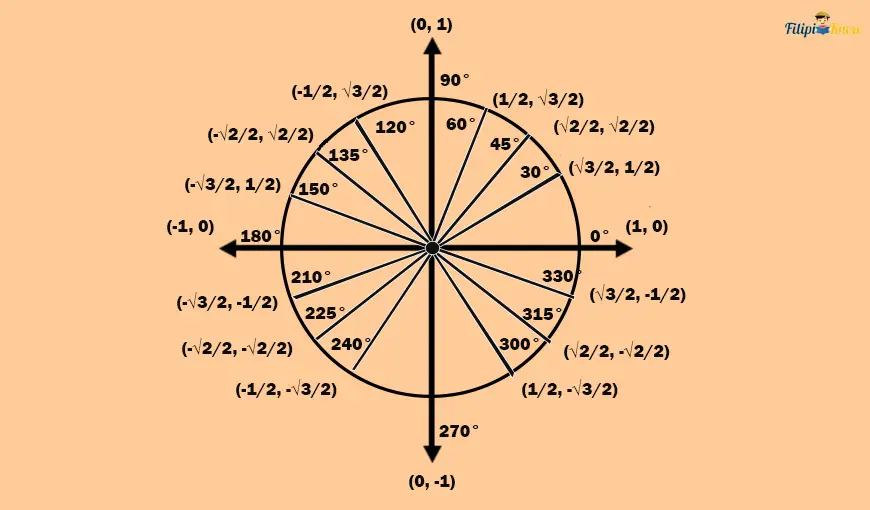
Using the coordinates above, we can determine the sine and cosine function values of each common angle in the unit circle.
1. Common Angles in the First Quadrant
| Angle | Sine | Cosine |
| 0° or 0 rad | 0 | 1 |
| 30° or π⁄6 rad | ½ | √3/2 |
| 45° or π⁄4 rad | √2/2 | √2/2 |
| 60° or π⁄3 rad | √3/2 | ½ |
| 90° or π⁄2 rad | 1 | 0 |
2. Common Angles in the Second Quadrant
| Angle | Sine | Cosine |
| 120° or 2π⁄3 rad (reference angle is 60°) | √3/2 | -½ |
| 135° or 3π⁄4 rad (reference angle is 45°) | √2/2 | – √2/2 |
| 150° or 5π⁄6 rad (reference angle is 30°) | ½ | – √3/2 |
| 180° or π rad (reference angle is 0°)` | 0 | -1 |
3. Common Angles in the Third Quadrant
| Angle | Sine | Cosine |
| 210° or 7π⁄6 rad (reference angle is 30°) | -½ | – √3/2 |
| 225° or 5π⁄4 rad (reference angle is 45°) | – √2/2 | – √2/2 |
| 240° or 4π⁄3 rad (reference angle is 60°) | – √3/2 | -½ |
| 270° or 3π⁄2 rad (reference angle is 90°) | -1 | 0 |
4. Common Angles in the Fourth Quadrant
| Angle | Sine | Cosine |
| 300° or 5π⁄3 rad (reference angle is 60°) | – √3/2 | ½ |
| 315° or 7π⁄4 rad (reference angle is 45°) | – √2/2 | √2/2 |
| 330° or 11π⁄6 rad (reference angle is 30°) | -½ | √3/2 |
| 360° or 2π rad (reference angle is 0°) | 0 | 1 |
After looking at the table above, you might ask yourself this question: Do I have to memorize all these values? If you want to save time deriving the values of each common angle above using reference angles, then it’s recommended to memorize them. However, it is also helpful that you know the technique on how to derive them so that in case your memory doesn’t serve you well, you have the mathematical tools to obtain them.
Tangent Function of a Central Angle of a Unit Circle
We have already defined the sine and cosine function of a central angle. But what about the tangent function? How do we derive it?
Recall that the tangent function is just the ratio of the sine function of an angle to the cosine function of an angle. In symbols:
tan θ = sin θ/cos θ
Since the sine of the central angle θ is defined as the y-coordinate of the point that the terminal side touches and the cosine of the central angle θ is defined as the x-coordinate of the point that the terminal side touches, then the tangent of the central angle θ is just:
tan θ = y/x
Let us have some examples:
Sample Problem 1: Determine the value of the tangent function of 0°.
Solution: The point on the unit circle at 0° or 0 radians is (1, 0). So, we have x = 1 and y = 0
Since tan θ (where θ is a central angle) is defined as y/x, then tan(0°) = 0/1 = 0
Thus, tan(0°) = 0.
Sample Problem 2: Calculate the value of tan(135°).
Solution: 135° is located in the second quadrant, so we have to use its reference angle to determine its corresponding coordinate.
The reference angle of 135° is |180° – 135°| = 45°. 45° corresponding point is (√2/2, √2/2).
Since 135° is in the 2nd quadrant with negative x-coordinates but positive y-coordinates, its corresponding point is (- √2/2, √2/2).
We can now define tan(135°).
Since 135° has a corresponding point of (- √2/2, √2/2), then x = – √2/2 and y = √2/2. This means that:
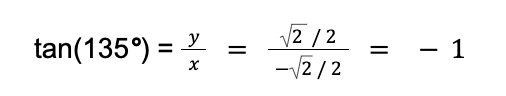
Thus, tan(135°) = -1.
Sample Problem 3: What is tan(330°)?
Solution: 330° is in the fourth quadrant, so we need its reference angle to determine its corresponding point.
The reference angle of 330° is |360° – 330°| = 30°.
The point on the unit circle at 30° is (√3/2, 1⁄2). This point is also the point for 330° but with different signs.
The coordinates in the fourth quadrant have positive x-coordinates but negative y-coordinates. Thus, the point on the unit circle at 330° must be (√3/2, -1⁄2).
This implies that we have x = √3/2 and y = -½.
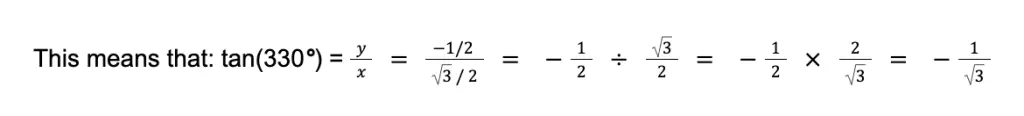
Thus, tan(330°) = – 1/√3. If we rationalize the denominator of this radical, we have – √3/3.
Sample Problem 4: Identify the value of the tangent of π radians.
Solution: π radians are equivalent to 180°.
The point on the unit circle at 180° is (-1, 0). Thus, we have x = -1 and y = 0.
Thus, tan(180°) = y/x = 0/-1 = 0.
Therefore, tan(180°) = 0.
The Secant, Cosecant, and Cotangent Functions
Just like in the right triangle trigonometry, the secant, cosecant, and cotangent function values of a central angle are the reciprocal of sine, cosine, and tangent functions, respectively:
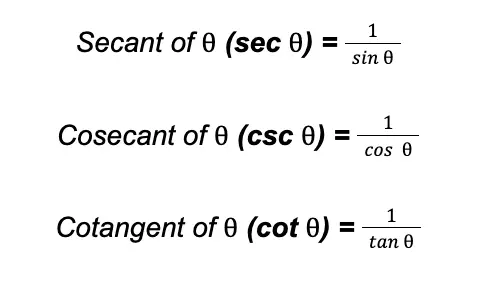
Since in circle trigonometry we are using the coordinate (x, y) which is touched by the terminal side of the central angle on the unit circle, then we can express the values of the secant, cosecant, and cotangent as follows:
Where x and y are the coordinates of (x, y) or the point touched by the terminal side of the given angle on the unit circle and x ≠ y ≠ 0.
Sample Problem: Calculate the values of sec θ, csc θ, and cot θ if θ = 45°.
Solution: The point on the unit circle at θ = 45° is (√2/2, √2/2). So, we have x = √2/2 and y = √2/2.
Next topic: Measures of Central Tendency
Previous topic: The Six Trigonometric Functions
Return to the main article: The Ultimate Basic Math Reviewer
