Chemical kinetics is the branch of chemistry that deals with the study of the speed or the rate at which chemical reactions occur. 

As you know, chemical reactions vary in the speed at which they occur. As an example, the conversion of 11-cis-retinal to rhodopsin, one of the series of chemical reactions that occur in our eyes that allows us to perceive colors, occurs in a matter of 10^─12 to 10^─6 seconds. In contrast, the conversion of graphite to diamond takes thousands, if not millions, of years to complete. In this module, we will learn more about the kinetics of chemical reactions.

Click below to go to the main reviewers:

Ultimate UPCAT Reviewer

Ultimate NMAT Reviewer

Ultimate LET Reviewer

Table of Contents

• The Concept of Chemical Kinetics
• Writing Rate Expressions
• Writing Rate Law Expression
  • 1. The Method of Initial Rates
  • 2. Integrated Rate Laws
• References
• Download Article in PDF Format
• Test Yourself!
  • 1. Practice Questions [PDF Download]
  • 2. Answer Key [PDF Download]

The Concept of Chemical Kinetics

Regardless of the nature of a chemical reaction, the rate at which the reaction proceeds is not constant all throughout. Take a look at the illustration below.

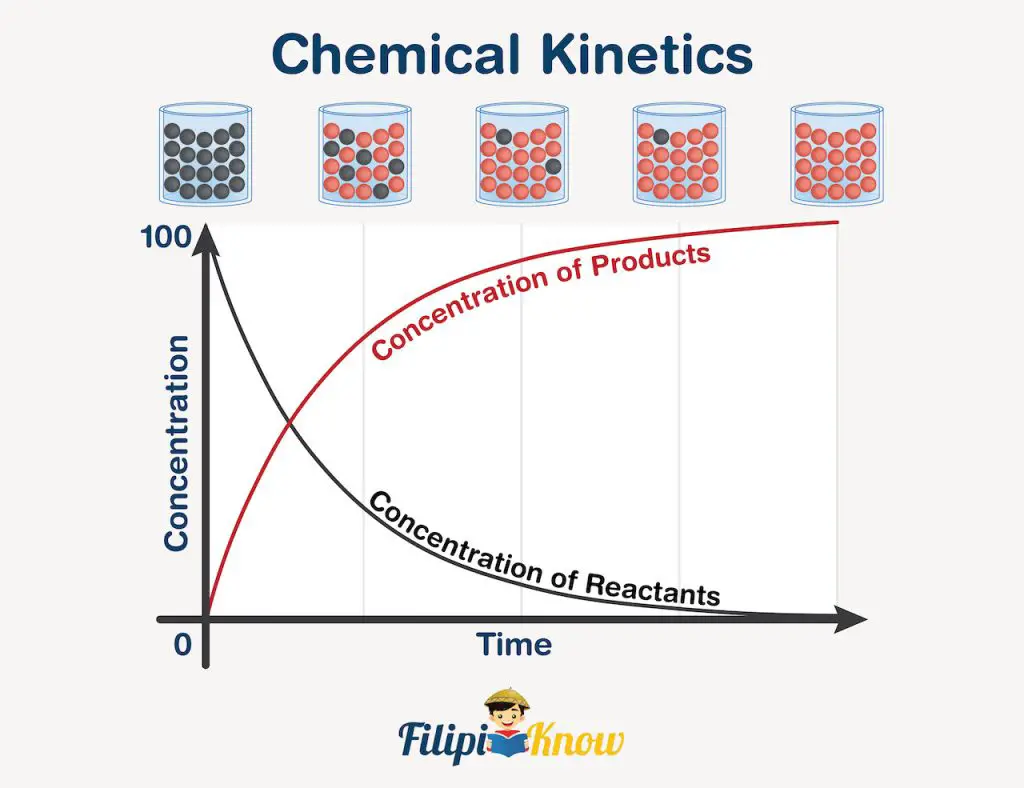
Initially, the beaker on top of the illustration contains black molecules only, indicating that it is the reactant. As time goes by, the black molecules are slowly being replaced by the red molecules (the product), until such time that only red molecules are present, meaning, the reaction goes to completion without any excess reactant.

Now, if you look at the graph, the black curve depicts the rate at which the reactant is being used up. You can see that as time passes, the number of molecules decreases, which is only logical because reactants are the ones being used up in a chemical reaction, so their amount is expected to decrease through the course of the reaction. The opposite is true for the red curve, showing an increase in the number of molecules as time passes due to the formation of the products.

However, regardless of the graph you take, you can see that the rate varies at any given point in the curve. This rate is called the instantaneous rate and can be obtained graphically by drawing a straight line tangential to only one point in the curve. For both the reactant and the product, the instantaneous rate is faster at the beginning of the reaction simply because the abundance of reactants causes the reaction to proceed faster. Nonetheless, as more and more products are being formed, the reactants become fewer and fewer, and for reactions with multiple reactants, this makes the reactants harder to “meet” one another, causing a decrease in reaction rate.

In this review, you will learn how to write rate expressions and the methods usually used to determine reaction rates in a chemical laboratory.

Writing Rate Expressions

In a certain hypothetical reaction 

aA + bB ⟶ cC + dD

A and B are known as the reactants, C and D are the products, while a, b, c, and d are the numerical coefficients of a balanced chemical reaction. As the reaction proceeds, A and B are being used up, while C and D are being formed. For such reaction, the rate of formation of products can be written as follows:

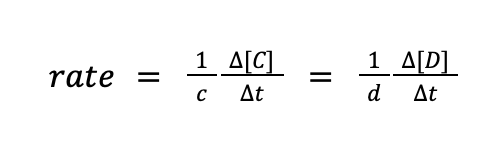
where Δ[C] and Δ[D] pertain to the change in concentration of C and D, respectively, while Δt pertains to change in time (t₂ – t₁). Meanwhile, the rate of disappearance of the reactants can also be written in the same manner.

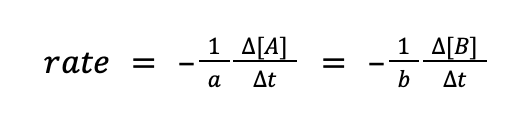
The question is, why negative? Does a negative rate really exist? The answer is that the negative sign does not necessarily mean that the rate of reaction is negative. Instead, it signifies that the species is being used up as the reaction proceeds.

Combining these two equations for the disappearance of the reactants and the formation of products: 

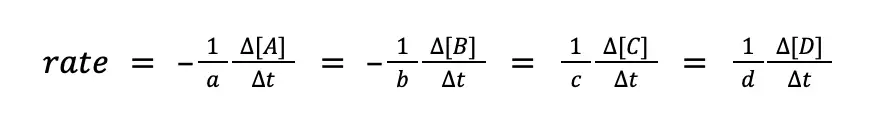
Sample Problem:

In the reaction shown below, it was found that ammonia is being used up at a rate of 0.34 M/s.

NH_3(g) + O_2(g) ⟶ NO_(g) + H₂O_(g)

1. Write the rate expression for the disappearance of the reactants and the formation of products.
2. At what rate are NO_(g) and H₂O_(g) forming? At what rate is O_2(g) disappearing?

Solution:

The first thing you need to do is to check if the reaction is balanced as presented. In this case, it is not yet balanced. Balancing the reaction will give

4NH_3(g) + 5O_2(g) ⟶ 4NO_(g) + 6H₂O_(g)

Now that the reaction is balanced, the rate expression can now be written.

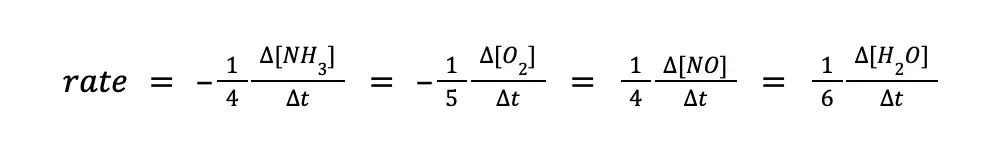
From the given, ammonia is being used up at a rate of 0.34 M/s. Hence, it can be written as:

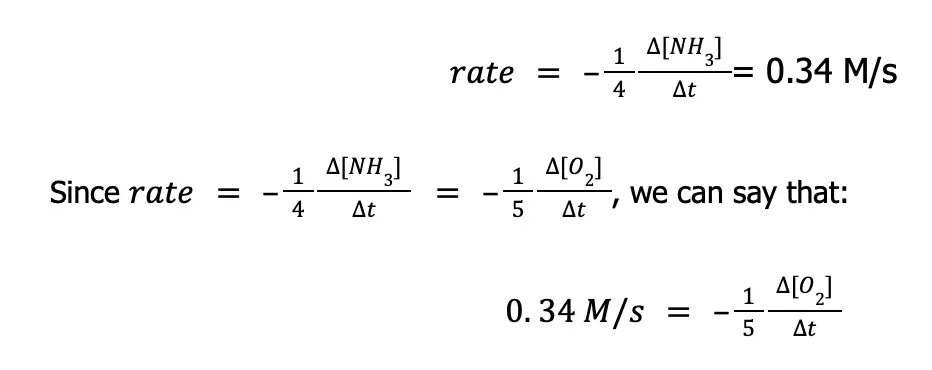
Now, to solve the rate at which O_2(g) is being consumed, we just need to isolate the term ∆[O2]⁄∆t from the equation above. To do that:

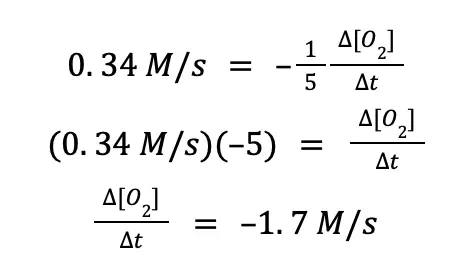
The same set of steps can be done to compute the rate at which NO_(g) and H₂O_(g) is produced.

Writing Rate Law Expression

So far, we’ve been able to write rate expressions in terms of the disappearance of reactants and the formation of the products. Rate law, on the other hand, expresses the relationship between the rate of reaction to the rate constant (k) and the concentration of the reactants raised to some powers.

For a hypothetical reaction

aA + bB ⟶ cC + dD

the rate law can be expressed as

rate = k[A]^x[B]^y

where x and y are known as the reaction orders with respect to A and B, respectively.

Always remember that rate laws are always expressed in terms of the concentration of the reactants only. Furthermore, the reaction orders x and y are not necessarily equal to the numerical coefficient of the balanced chemical reaction, and hence must be determined experimentally.

The two known methods to calculate reaction orders from experimental data are the method of initial rates and the use of integrated rate laws.

1. The Method of Initial Rates

In this method, you will be given the initial concentration of all the reactants and the initial rate of the reaction. Using the initial rate is more convenient because as the reaction proceeds, the concentration of the reactant decreases and can be difficult to measure at any given time. Furthermore, the reverse reaction from product to reform the reaction may also occur, and these scenarios will complicate the calculation of reaction orders.

Let us work with some examples to demonstrate the method of initial rates.

Sample Problem:

At a certain temperature, the following data were obtained for the reaction of peroxydisulfate ion with iodide ion.

S₂O₈^2–_(aq) + 3I^–_(aq) ⟶ 2SO₄^2–_(aq) + I₃^–_(aq)

Experiment	[S2O82–], M	[I–], M	Initial Rate, M/s
1	0.160	0.068	2.2 x 10–4
2	0.160	0.034	1.1 x 10–4
3	0.320	0.034	2.2 x 10–4

1. Determine the reaction order with respect to peroxydisulfate ion and iodide ion.
2. Write the rate law expression for the reaction.
3. Identify the overall reaction order and the molecularity of the reaction.

Solution:

 From the reaction given above, the rate law expression can be written as

rate = k[S₂O₈^2–]^x[I^–]^y

To determine the reaction order, the general approach is to get the ratio of any two rate law expression using the data provided. That is:

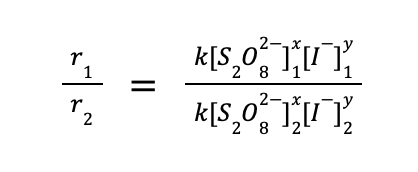
The question is, how to choose which experimental data to use. The trick is to choose two runs wherein the concentration of only one reactant varies, and is constant for the rest of the other reactants. From the data given to us, we can use experiments 1 and 2, wherein [S₂O₈^2–] is the same, while [I^–] varies. Substituting the values to the equation above:

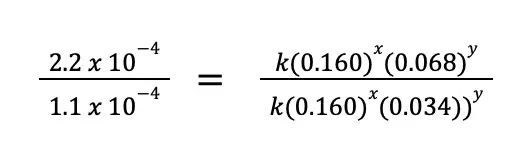
From this equation, we can immediately cancel k(0.160)^x since it will just be equal to 1. Take note that we did not write k₁ and k₂ because the rate constant only varies if the temperature varies. In this example, the temperature is constant. Simplifying the equation:

For more complicated equalities, you can take the logarithm of both sides, then manipulate the equality. That is:

The same procedure can be done to solve for x.  But this time, we will use experiments 2 and 3 so that [S₂O₈^2–] varies, while [I^–] is constant.

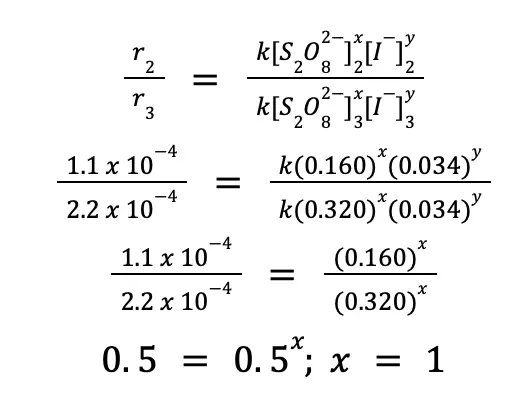
Therefore, the complete rate law expression for the reaction is 

rate = k[S₂O₈^2–][I^–]

To interpret this result, we can say that the reaction is first order with respect to [S₂O₈^2–] and  [I^–], which simply means that the concentration of either of the two reagents affects the overall reaction rate.

You will encounter reactions that are zeroth-order with respect to at least 1 reactant. That means that regardless of the concentration of that reactant, the rate will be unaffected. When asked about the overall reaction order, it is the sum of all the reaction orders in the rate law expression. Hence, for this example, the overall reaction order is 2.

Meanwhile, molecularity pertains to the number of reactant particles involved in the chemical reaction which affects the reaction rate. Since both S₂O₈^2– and I^– dictate the rate of the above-mentioned reaction, then the reaction is said to be bimolecular.

2. Integrated Rate Laws

Integrated rate laws are equations that relate the concentrations of reactants to the elapsed time of the reaction. Determining whether the reaction is zeroth order, first-order, second-order (or higher) with respect to a certain reactant requires determining the linearity of the plot when certain points are plotted against time.

The table below summarizes the kinetics of zeroth- to second-order reactions.

Table 1. Summary of the kinetics of a zeroth-, first-, and second-order for a reaction where A ⟶ products.

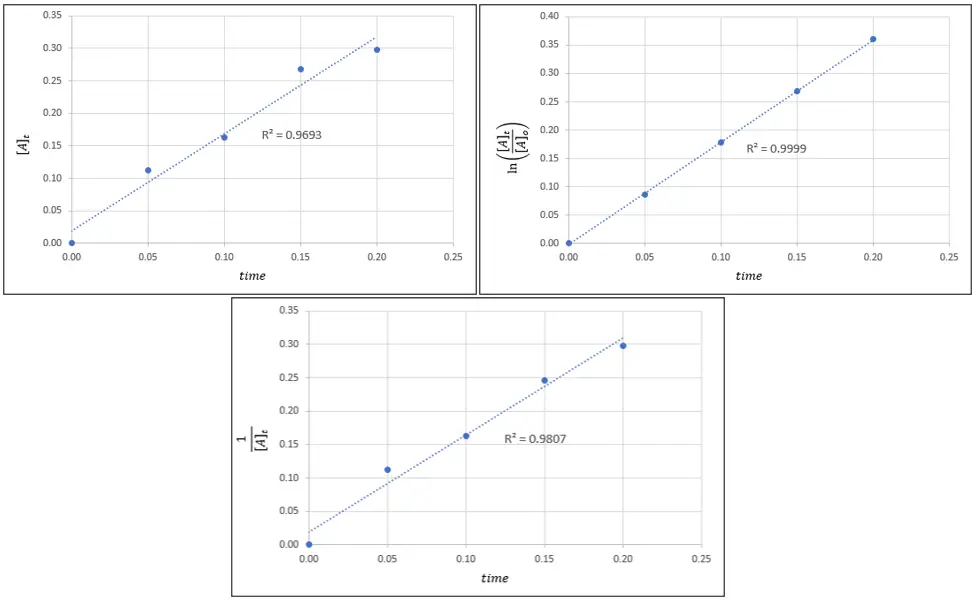
In this method, three different plots are made, and the curve that will have the highest coefficient of determination (r²) will be the order of the reaction. Because of the manner in which this method is being used to determine rate law, most likely you will need a calculator. However, just because you need a calculator does not mean that there is no chance that you will encounter this kind of problem in the exam. Take a look at the example below.

Sample Problem:

Based on the illustration given below, which of the following is the correct rate law expression for the decomposition reaction of ethane (C₂H₆) to methyl radicals?

C₂H_6(g) ⟶ 2CH_3(g)

a. rate = k

b. rate = k[C₂H₆]

c. rate = k[CH₃]

d. rate = k[C₂H₆]²

Solution:

From the given choices, you can immediately eliminate option C because rate law expressions are expressed in terms of the reactants only, and option C is expressed in terms of product based on the given chemical reaction. 

To determine the correct answer among choices A, B, and D, bear in mind that the curve with the highest r² will be the order of the reaction. From the illustration, the graph with the highest r² is the one on the top right corner which is achieved when ln([A]t/[A]o)is plotted against time.

From Table 1, we can say that this graph corresponds to a first-order reaction. Hence, the correct rate law expression is rate = k[C₂H₆].

References

Chang, R. (2010). Chemistry (10th ed.). New York City, USA: McGraw-Hill Companies, Inc.

Kotz, J. (2022). Chemistry and Chemical Reactivity. Stamford, CT: Cengage Learning.

Zumdahl, S., Zumdahl, S., & DeCoste, D. (2010). Chemistry (8th ed.). Belmont, California: Brooks Cole.

Next topic: Chemical Equilibria

Previous topic: Chemical Reactions

Return to the main article: The Ultimate Chemistry Reviewer

Download Article in PDF Format

Test Yourself!

1. Practice Questions [PDF Download]

2. Answer Key [PDF Download]