Molarity, Molality, and Normality: Reviewing Concentration of Solutions

The study of solutions entails knowing their concentration or the amount of solute present in a solution.
Scientists and chemists use a lot of different concentration units. You probably don’t realize it, but we are dealing with concentrations almost every day. For instance, do you know someone, probably a friend, who is very conscious about the food he/she eats? I happened to know one, and whenever we go to the supermarket to buy food and snacks, the first thing she does is look for the nutrition facts and find how much carbohydrates/sugars are in that food.
You may not know it, but nutrition facts are essentially an expression of the concentration of each component present in the product. Some nutrition facts are expressed in terms of mass, while others are in percentage. In this module, you will learn the commonly used concentration units.
Click below to go to the main reviewers:
Table of Contents
- Percentage Composition
- Parts per Million and Parts per Billion
- Molarity
- Molality
- Normality
- Sample Problem 1
- Sample Problem 2
- References
- Download Article in PDF Format
- Test Yourself!
Percentage Composition
Percentage composition is probably the most used in expressing concentrations, as it is easier to understand, especially for individuals with no background in chemistry. Percent composition is the proportion of a certain substance relative to the entirety of the system being considered.
For example, when we say 70% ethyl alcohol, we are saying that if we have 100 mL of that solution, 70 mL of that would be ethyl alcohol, and the remaining 30 mL will be the other components of the solution. Going deeper into this topic, percentage composition can be expressed in per weight basis (% w/w), per volume basis (% v/v), and in weight per volume basis (% w/v).
You might ask, why are there so many ways of expressing percentage composition? Well, the answer is mainly for convenience. This might not be very common, but actually, there are solid solutions, one example of which is dental amalgam, a filling material used to fill cavities caused by tooth decay. This solution comprises various metals, but its main component is elemental mercury which is approximately 50% by weight.
If the solution’s components are all solids, then the most convenient way of expressing its concentration is on a per weight basis (% w/w). That way, when we say dental amalgam is 50% (w/w) Hg, it can be conveniently understood that if there is 100 g of dental amalgam, 50 g of it is mercury.
Per volume basis (% v/v) becomes more appropriate if the solution’s components are all liquids. For example, the components of 70% (v/v) aqueous ethyl alcohol are usually ethyl alcohol and water only. Specifying that the solution is 70% (v/v) ethyl alcohol implies that in a 100 mL solution, ethanol is 70 mL and water is only 30 mL.
Lastly, there are solutions wherein some of the components are initially solid while other components are liquid. Say you’ve added 23 g of table salt (NaCl) in water to make 100 mL of aqueous NaCl solution. In such cases, the concentration can be better expressed per weight by volume basis. With that, we can conveniently express the concentration of the described solution as 23% (w/v) NaCl solution.
However, just because a solution has a concentration of 70% (v/v) ethyl alcohol doesn’t mean it cannot be expressed in terms of % (w/w) and % (w/v). It is still possible but slightly inconvenient because the density of the substance being considered must be accounted for, as 1 mL of most substances is probably not equal to 1 g of that substance. Mathematically, these concentration units can be expressed as follows:
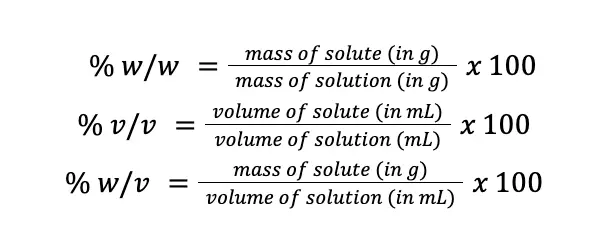
Take note that before multiplying by 100, make sure that the unit of mass is in grams and the unit of volume is in mL to avoid errors in calculations.
Parts per Million and Parts per Billion
Analysis of trace components usually involves expressing a very minute amount of a certain solute relative to the amount of the solution. To put it into perspective, imagine you are analyzing lead in a deep well, and your findings suggest that the concentration is 0.0000051% (w/v) Pb, or in scientific notation, 5.1 x 10-6 %(w/v). It’s quite awkward to express concentration like this, right? That’s why parts per million (ppm) and parts per billion (ppb) are usually used to express very minute concentrations.
For dilute solutions, parts per million (ppm) and parts per billion (ppb) are usually more appropriate. Mathematically:
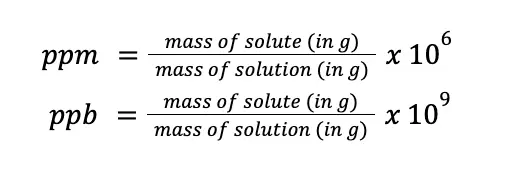
Take note that what is shown here is on a per weight basis, but ppm and ppb can also be expressed in terms of per volume and weight per volume basis. Also, notice that the formulas are almost the same as the formulas used for percentage composition, except that instead of 100, the multiplier for ppm and ppb are 106 and 109, respectively.
Molarity
From this point forward, we will deal with more technical ways of expressing concentrations. The expression of concentrations is commonly used by scientists in declaring the concentration of solutions.
Molarity (designated as M) is defined as the number of moles of solute present in a liter of a solution. The unit of molarity is mol/L, or simply “M” (read as molar). Mathematically:

Furthermore, recall that the number of moles of solute can be calculated by dividing the mass of the solute by its molar mass.
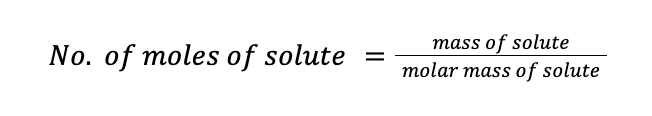
Molality
Molality (designated as m) is defined as the number of moles of solute present per kilogram of solvent. The unit of molality is mol/kg solvent, or simply “m” (read as molal). Mathematically:
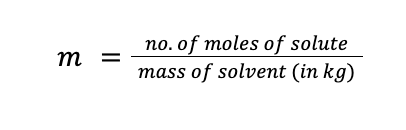
Normality
Normality is a concentration unit usually used in solutions of acids and bases and oxidizing and reducing reagents. Normality (designated as N) is the ratio of gram equivalent of solute and the volume of the solution in liters. The unit of normality is equivalent/L, or simply “N” (read as normal). Mathematically:

Gram equivalent of solute can be calculated by dividing the mass of the solute by the solute’s equivalent weight (EW), where EW can be further calculated by dividing the molar mass by the number of equivalents (n) of that solute.
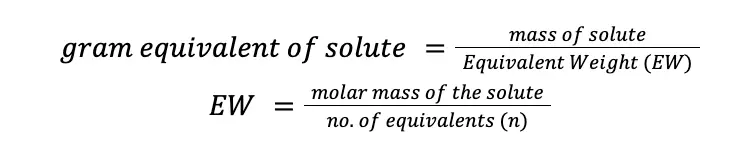
For acids, the number of equivalents (n) is equal to the number of protons that the acid can donate. The equivalents for acids HCl, H2SO4, and H3PO4 are 1, 2, and 3, respectively. For basic solutions, the number of equivalents equals the number of hydroxide ions (─OH) that can ionize in the solution. Hence, the number of equivalents of NaOH, Ca(OH)2, and Al(OH)3 are 1, 2, and 3, respectively.
Sample Problem 1
A sample of kitchen vinegar was found to contain 6.00 % (w/v) acetic acid, CH3COOH (MM = 60 g/mol). If the density of the vinegar sample is 1.06 g/mL, what is the concentration of acetic acid in (a) % (w/w); (b) molarity; (c) normality; and (d) molality.
Solution
First, let us assume that we have 100 mL of vinegar. From that 100 mL, 6.00 g is acetic acid since the vinegar contains 6.00 % (w/v) acetic acid. To find the concentration of acetic acid in % (w/w), we can convert the volume of vinegar to mass by using its density. That is:

Now that we know the mass of vinegar, we can use the formula for % (w/w).

To solve for molarity, we can convert mass to the number of moles using the molar mass of acetic acid, then we also convert the volume of acetic acid from mL to liters.
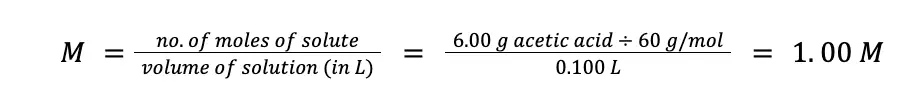
Meanwhile, to solve for normality, acetic acid is a weak monoprotic acid, which implies that n = 1. Hence, it can be said that MM = EW.
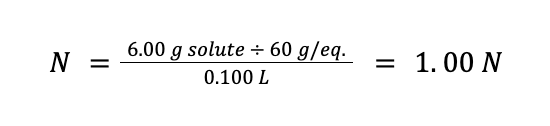
Lastly, to solve for molality, we know that the mass of the vinegar solution is 106 g, wherein 6 g is acetic acid. Therefore, the mass of the solvent in our example is 106 g – 6 g = 100 g. Solving for the molality:
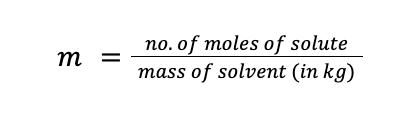
TIP: When interconverting molarity and normality, you can use the formula N = Mn.
Sample Problem 2
What is the molarity and normality of a Ca(OH)2 (MM = 74 g/mol) solution if a 500 mL solution contains exactly 7.400 g of pure Ca(OH)2?
Solution
Solving for the molarity:
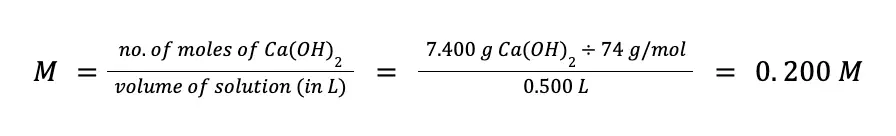
When ionized in water, a mole of Ca(OH)2 releases two moles of ─OH according to the reaction
Ca(OH)2(s) ➝ Ca2+(aq) + 2 ─OH(aq)
Hence, for Ca(OH)2, n = 2. Solving for the normality:
N = Mn = (0.200)(2) = 0.400 N
References
Chang, R. (2010). Chemistry (10th ed.). New York City, USA: McGraw-Hill Companies, Inc.
Silberberg, M. (2006). Chemistry: The molecular nature of matter and change (4th ed.). New York City, USA: McGraw-Hill Companies, Inc.
Zumdahl, S., Zumdahl, S., & DeCoste, D. (2010). Chemistry (8th ed.). Belmont, California: Brooks Cole.
Next topic: Organic Chemistry
Previous topic: Nuclear Chemistry
Return to the main article: The Ultimate Chemistry Reviewer
Download Article in PDF Format
Test Yourself!
1. Practice Questions [PDF Download]
2. Answer Key [PDF Download]
Written by John Bryan Rolloque
in College Entrance Exam, LET, NMAT, Reviewers, UPCAT
John Bryan Rolloque
John Bryan Rolloque graduated cum laude at the University of the Philippines Los Baños in 2018 under the B.S. Agricultural Chemistry program. He taught courses in general chemistry, analytical chemistry, and organic chemistry at UPLB’s Institute of Chemistry, and has been serving as the Region IV coordinator for the Regional and National Chemistry Olympiad. Landing 8th place in the 2019 licensure exam for agriculturists, he is now taking up his master’s degree in plant physiology, also in UPLB.
Copyright Notice
All materials contained on this site are protected by the Republic of the Philippines copyright law and may not be reproduced, distributed, transmitted, displayed, published, or broadcast without the prior written permission of filipiknow.net or in the case of third party materials, the owner of that content. You may not alter or remove any trademark, copyright, or other notice from copies of the content. Be warned that we have already reported and helped terminate several websites and YouTube channels for blatantly stealing our content. If you wish to use filipiknow.net content for commercial purposes, such as for content syndication, etc., please contact us at legal(at)filipiknow(dot)net
