So far, we’ve only learned about Newtonian physics applied to relatively slow-moving objects. But what if we’re observing objects moving near the upper limit of speed, i.e., the speed of light? Can the same laws of physics still be used to describe these objects? 

In this chapter, you will learn the basics of one of the most intriguing and controversial theories proposed in the early 1900s, the special theory of relativity.

Click below to go to the main reviewers:

Ultimate UPCAT Reviewer

Ultimate NMAT Reviewer

Table of Contents

• Theory of Relativity
• Reference Frames
• Time Dilation
• Length Contraction
• References
• Download Article in PDF Format
• Test Yourself!
  • 1. Practice Questions [PDF Download]
  • 2. Answer Key [PDF Download]

Theory of Relativity

Classical relativity is a field of study that deals with simple transformations and observations involving two reference frames that can be stationary or moving relative to one another. 

Imagine walking inside a moving bus, and an observer standing at a nearby bus station saw you while walking. If that observer studies your speed as you move away from him/her, the observer will logically think that you are moving at the speed of the bus plus the speed of your walking. However, if the observer is inside the bus, it would be a different story. Since the second observer is moving with the bus, he/she will only consider your walking speed. Classical relativity was first defined by Galileo, which was later on, refined by Isaac Newton.

Now, let’s level up things a bit. What if the bus you were riding earlier travels at speed approaching the speed of light? Observations of these systems were accurately predicted by Albert Einstein’s theory of relativity, which is subdivided into the special and general theories of relativity. 

In a much deeper sense, the special theory of relativity explains how time and space are related. It is Einstein’s answer in his attempt to explain the inconsistency between Newtonian mechanics and Maxwell’s equation. Though for our purpose, it is enough to define that the special theory of relativity predicts how events are measured with respect to different observers who can be in motion with respect to the said event. 

Why is it special, you might ask? Well, this is because each observer is considered to have a special type of reference frame, an inertial reference frame!

An object in motion will stay in motion, and an object at rest will stay at rest. So imagine you are observing a rolling billiard ball on a billiard table. Under an inertial reference frame, the ball will not stop rolling. In other words, no other external force acts on the ball. Now, if we account for the influence of gravity on the ball, this is where the general theory of relativity comes in. Due to its complexity, we will not be dealing with the generalized theory in this material.

Going back to the special theory, remember the bus example given earlier? Let’s tweak the same example a little bit, and instead of you being a passenger walking inside the moving bus, let’s say that you are the bystander in the nearby station. 

While waiting for your ride, you saw a bus traveling at a speed of 15 m/s that suddenly turned on its light. Being a physics geek, you asked yourself: Does the light from the bus travel at c (c ≈ 3 x  10⁸ m/s), or is it c + 15 since the light source (aka the bus) travels at a speed of 15 m/s? That’s a mind-boggling question.

Thankfully, Einstein’s special theory of relativity offers us the answer to this question through its two postulates:

Postulate 1:	The relativity postulate: The laws of physics are the same in all inertial reference frames.
Postulate 2:	The speed of light postulate: The speed of light in a vacuum, c, always has the same value in all inertial reference frames, no matter how fast the observer and the light source are moving relative to each other.

Reference Frames

In this chapter, we will focus our discussion on special relativity. By definition, special relativity is a theory used in predicting how observations are measured with respect to various observers who can be moving or stationary relative to the phenomenon being observed. Why is that important, you ask? Let’s focus first on the illustration given below to answer that question.

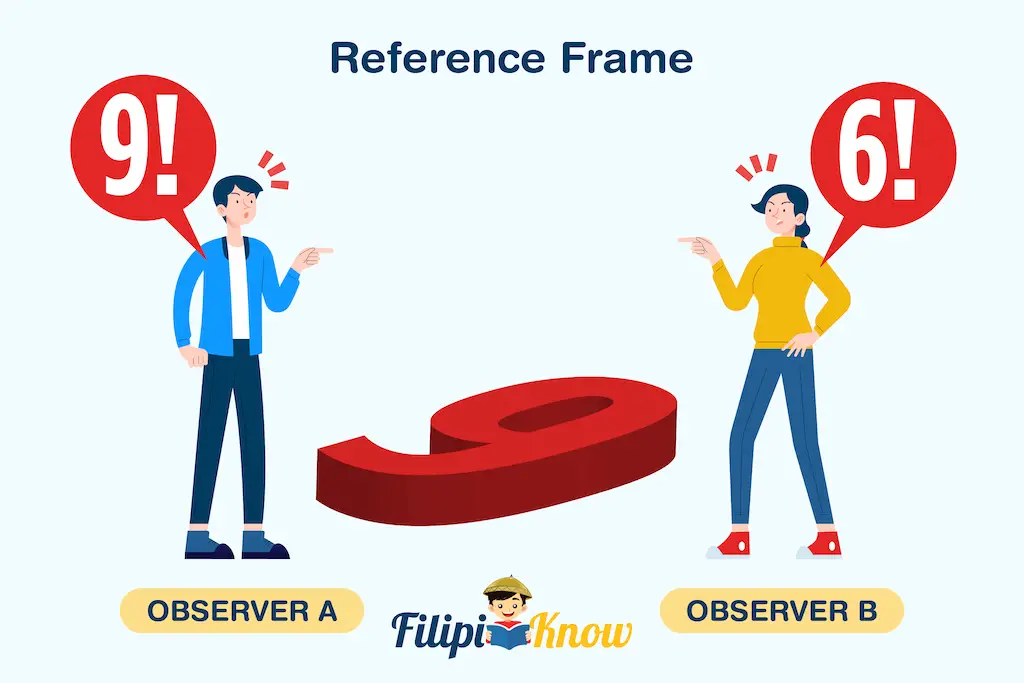
In the illustration, two observers view the same object (or scenario) from different perspectives. One observer saw the object as 6, while the other was 9. So which of them is correct? Both of them are correct! The difference in their perspective (which we will later call reference frames) causes the difference! So one takeaway from the special theory of relativity is that if life seems hard, try looking at it from a different perspective.

When studying the theory of relativity, one important term that will always pop up is the reference frame. A reference frame (or frame of reference) is a coordinate system (or simply the exact place) and clock the observers carry with them.

This is hard to digest, but imagine standing in a bus station when a fire truck traveling at 100 kph suddenly passed in front of you. You will see the truck moving very fast, right? Meanwhile, on the other side of the bus station, another observer (probably your friend) riding on a bullet train traveling at 321 kph also saw the fire truck moving at the same speed at the exact moment you saw it.

At that specific moment, you and the other observer have distinct and specific coordinates in 3D space with their own time; hence, both of you have reference frames distinct from one another. And it goes without saying that due to the relative difference in the speed of the two observers, you might see the fire truck moving so fast, but the other observers see the truck moving slowly!

A reference frame is said to be inertial if it is not accelerating. It implies that Newtonian physics applies in inertial reference frames, i.e., an object in motion will stay in motion, and an object at rest will stay at rest.

Time Dilation

Have you ever heard of the phrase “time is relative”? Well, it turns out that this is supported by physics! The special theory of relativity predicted that time in two inertial reference frames moving with respect to each other will appear different. This phenomenon was termed time dilation. 

How is that even possible? Let’s imagine you are riding a rocket traveling at immense speed. In the rocket, you have a light clock wherein a beam of light bounces back and forth of a mirror facing parallel with one another, as seen in the illustration below.

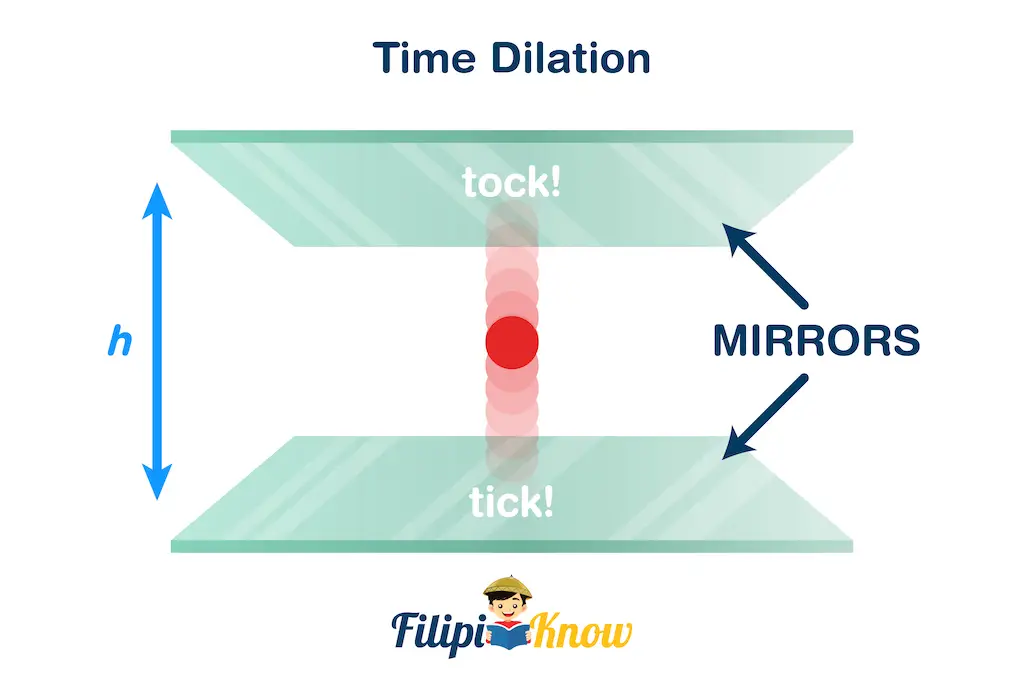
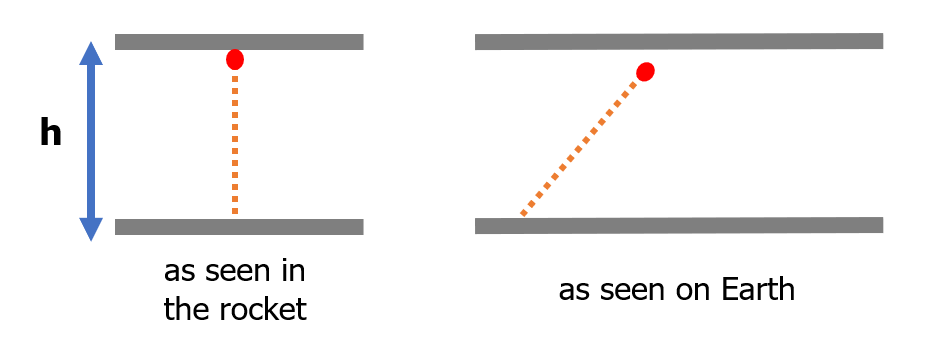
The time it takes for the light to bounce from the upper mirror to the lower mirror denotes a certain unit of time. Now for comparison, let’s say that you are on the Earth’s surface, and for some reason, you see the same light clock inside a transparent rocket. The illustration below shows the difference in how you will see the movement of each “tick” of the light clock when you’re riding the rocket (top of the illustration) and when you’re observing the light clock from the Earth’s surface (bottom of the illustration).

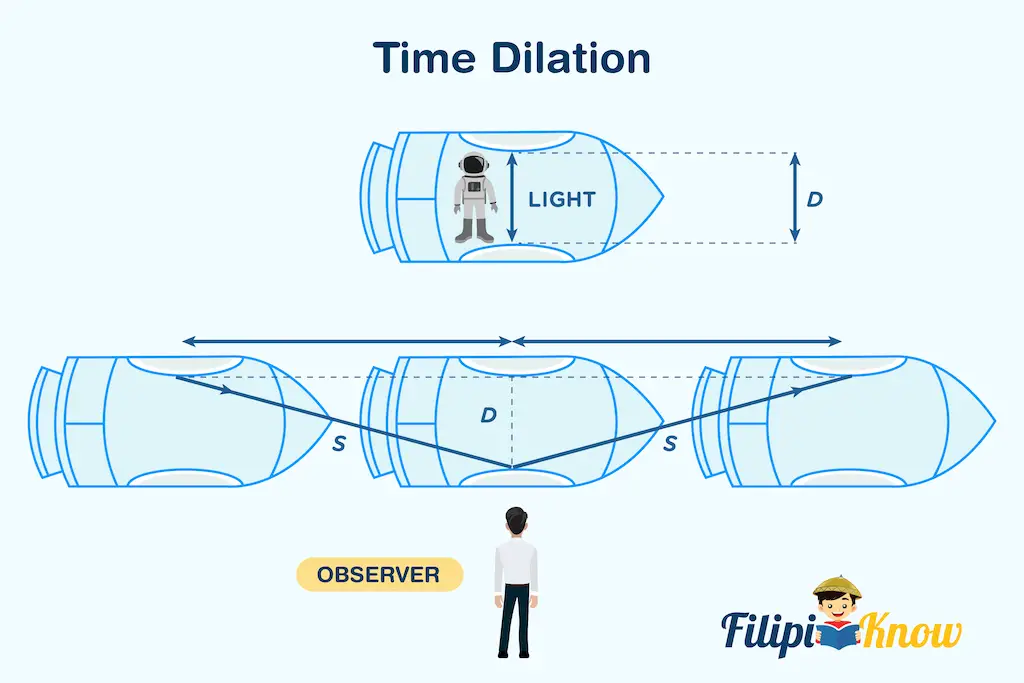
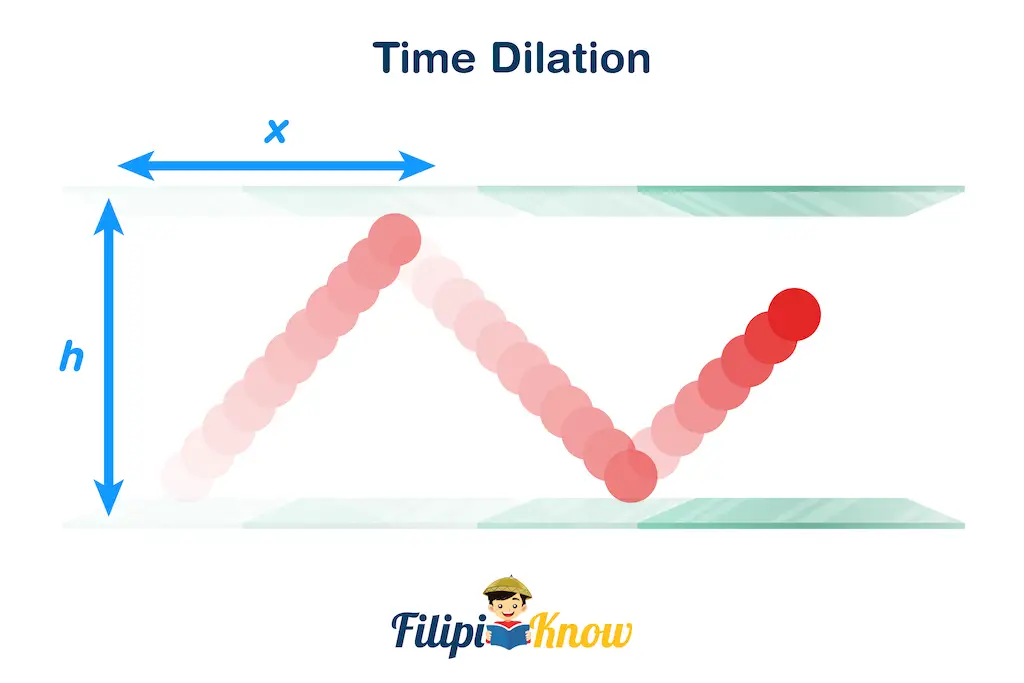
Due to the rocket moving at immense speed, an observer at the Earth’s surface will see the light inside of the light clock moving at a diagonal path (as shown in the illustration below) in contrast to the straight path that it travels relative to the observer inside of the rocket. In effect, due to apparent differences in the length the light needs to travel between the two observers, it looks like the time experienced by the observer inside the rocket is shorter than the time experienced by the observer on the Earth’s surface. This is time dilation!

Length Contraction

If you’re still unable to accept that time is relative, brace yourself because it turns out, according to the special theory of relativity, length (or space) is relative as well!

Recall from our illustrations in time dilation that observers on Earth tend to see the bouncing light in a light clock traveling through a diagonal path instead of a straight line. This difference is demonstrated in the next figure.

Although it is apparent that it looks like the light inside of the light clock indeed travels longer distances for the observer on Earth, we cannot say that light travels faster in that case because it will violate the speed of light postulate, which explicitly states that the speed of light always has the same value in all inertial reference frames.

To maintain the speed of light, something else must have happened here, especially because it has shown that time dilation cannot fully account for the observed discrepancy. The phenomenon that completes this picture is the length contraction. At higher speeds, length (or space) appears contracted, so although the rocket looks normal-sized to the passenger inside, it appears slightly shorter to the observer on Earth.

References

Holzner S. 2010. Physics II for dummies. USA: Wiley Publishing, Inc.

Young HD, Freedman RA. 2008. Sear’s and Zemansky’s university physics with modern physics. 12th ed. New York, USA: Pearson Education, Inc.

Previous topic: Nuclear Physics

Return to the main article: The Ultimate Physics Reviewer

Download Article in PDF Format

Test Yourself!

1. Practice Questions [PDF Download]

2. Answer Key [PDF Download]