Nuclear physics focuses on studying atomic nuclei and their interactions, with emphasis on how energy can be harnessed from these interactions.

The applications of nuclear physics are one of the most controversial issues nowadays. Depending on how we use it, its consequences can be as beneficial as the generation of a huge amount of energy with minimum CO₂ emissions in nuclear reactors or as destructive as massive explosions caused by nuclear weapons, such as atomic bombs.

In this chapter, you will learn the fundamentals of nuclear physics.

Click below to go to the main reviewers:

Ultimate UPCAT Reviewer

Ultimate NMAT Reviewer

Ultimate LET Reviewer

Table of Contents

• The Atomic Nuclei
• Nuclear Stability and Binding Energy
  • Rules in Predicting Nuclide Stability or Radioactivity
• Nuclear Fission and Fusion
• References
• Download Article in PDF Format
• Test Yourself!
  • 1. Practice Questions [PDF Download]
  • 2. Answer Key [PDF Download]

The Atomic Nuclei

Numerous experiments lead us to the currently accepted model of an atom being mostly space with its mass concentrated in the middle where the nucleus is located.

The nucleus is composed of neutrons and protons, and the total number of these particles in the nucleus is called the nucleon number. In chemistry, the nucleon number is also known as the mass number (A). 

Experiments have shown that based on nucleon number, atomic radius (R) can be calculated using the equation

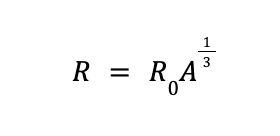
where R₀ is an experimentally determined constant equal to 1.2 x 10^—15 m or 1.2 femtometers (fm).

Because the nucleus comprises two types of subatomic particles, the atomic number also has two components. The number of protons is known as the atomic number (designated as Z), while the number of neutrons is called the neutron number (designated as N). As such, an atomic number can be expressed mathematically as

A = N + Z

A single nuclear species with a specific number of N and Z is called a nuclide. The shorthand notation for writing a nuclide of, say, element X is

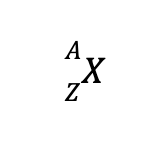
Another term you may encounter is the isotope, defined as species with the same number of protons (hence, same element) but differs in the number of neutrons. For instance, the element hydrogen has three known isotopes:

The second isotope is more commonly known as deuterium while the third isotope is more popularly known as tritium. Hence, they can also be written as:

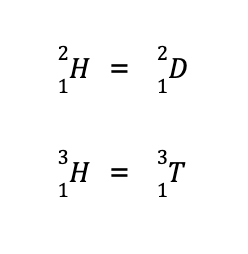
As you can see, all three isotopes have the same Z but differ in A. If we use the equation given above to solve for the number of neutrons for each hydrogen isotope, we arrive at:

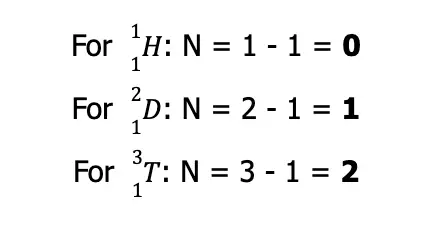
Nonetheless, although protium, deuterium, and tritium are isotopes of the same element, they are considered three distinct nuclides.

Nuclear Stability and Binding Energy

One of the important things that we should know when studying nuclear stability is the density of an atomic nucleus. In our general chemistry classes, we were taught that density is the ratio of the mass of a substance relative to its volume. In other words, density describes how compact a substance is. 

This might be quite surprising, but despite the atomic nucleus being unimaginably tiny, its density is incomprehensibly huge! To demonstrate this, let’s consider a nuclide that contains 30 protons and 30 neutrons. Using the equation for calculating atomic radii presented earlier, we can calculate the radius of the given nuclide.

With R₀ = 1.2 x 10^–15 m, and A equal to the sum of protons and neutrons, which happens to be equal to 60 in this case, we can predict that the radius (R) of the given nuclei is:

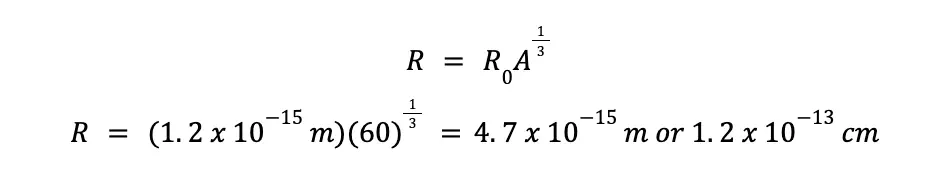
Furthermore, using the mass of each proton (1.67262 x 10^-24 g) and neutron (1.67493 x 10^-24 g), we can predict that the approximate mass of this nuclide is:

Mass = 30(Mass of Neutron) + 30(Mass of Proton)

Mass = (30 x 1.67493 x 10^-24 g) + (30 x 1.67262 x 10^-24 g)

Mass = 1.004265 x 10^-22 g

Note that the mass of electrons in this nuclide is assumed zero since its mass (9.10938 x 10^-28 g each electron) is thousands of magnitudes lighter than the mass of protons and neutrons.

Now, considering that the nucleus is spherical with a volume of 4⁄3πr³, we can compute the density as shown below:

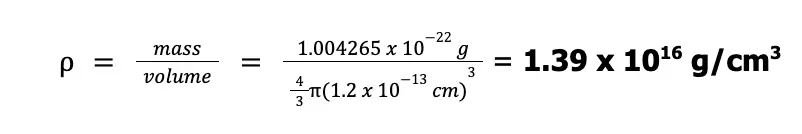
To help you visualize the density of an atomic nucleus, it was suggested that this density can be achieved by packing all the automobiles in the world in just one thimble (shown below)! How compact was that?!

Now, the question is, if the nucleus is that dense, what holds the particles together so tightly? Furthermore, let us not forget that Coulomb’s law predicts that particles with the same charges repel, yet positively-charged protons clump together closely in the nucleus. 

Well, it turns out that aside from repulsive forces, there also exists short-range proton-proton, proton-neutron, and neutron-neutron attractions! If the short-range attraction outweighs the Coulombic repulsion, the nucleons stay together, making the nuclide stable. Otherwise, it disintegrates and emits particles and/or radiation. With this, the stability of nuclides can be predicted by just looking at the number of protons and neutrons in them.

Rules in Predicting Nuclide Stability or Radioactivity

As mentioned, the principal determinant of nuclear stability is the neutron-to-proton ratio (n/p). The following rules can be used to predict whether a nuclide is stable or unstable/radioactive:

1. Nuclei which contain 2, 8, 20, 50, 82, or 126 protons or neutrons are generally more stable. In nuclear physics and chemistry, these numbers are termed “the magic numbers!”
2. Nuclei with even numbers of both protons and neutrons are generally more stable than those with odd numbers of these particles.
3. Isotopes with atomic numbers greater than 83 are radioactive. In addition to this, all isotopes of Tc (Z = 43) and Pm (Z = 61) are radioactive.

Furthermore, a plot of the number of neutrons vs. the number of protons (shown below) demonstrates that stable nuclides aggregate at the shaded region known as the belt of stability. The straight diagonal plot represents the plot where n/p = 1.

Radioactive nuclides with n/p greater than those in the belt lie above the belt of stability. To achieve stability, these nuclei undergo ꞵ-particle emission (or ꞵ decay) to lower their n/p ratio.

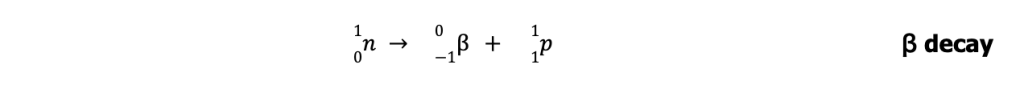
On the other hand, unstable nuclides with n/p lower than those in the belt lie below the belt of stability. To achieve stability, these nuclei undergo either positron emission or electron capture to increase their n/p ratio.

In electron capture, the nucleus captures one electron (usually 1s electron) and combines it with a proton to form a neutron. The process is accompanied by the emission of highly energetic gamma radiation.

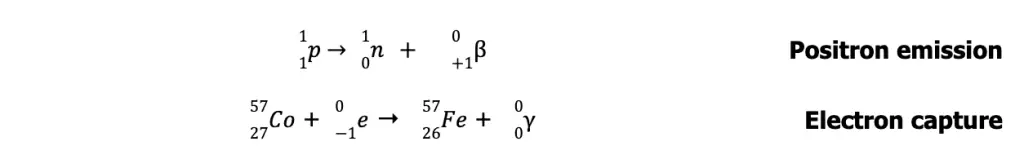
The quantitative measure of nuclear stability is the nuclear binding energy, defined as the energy required to break down a nucleus into its component neutrons and protons. The idea of binding energy originates from observations that actual atomic masses of nuclides are always lower than the atomic masses calculated from the known masses of protons and neutrons. 

To demonstrate, let us consider

What you see above is an isotope of fluorine with 9 protons and 10 neutrons. Based on the known masses of these subatomic particles, the calculated atomic mass of the aforementioned isotope is

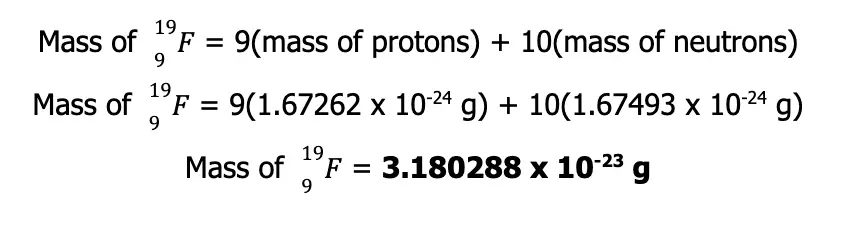
However, experimental measurements suggest that the actual mass of the nuclide is only 3.1548 x 10^-23 g. The difference between the actual and the calculated atomic masses of nuclides is called the mass defect. This defect can be explained by Einstein’s famous equation, which states that

E = mc²

where E is energy, m is mass, and c is the speed of light equal to 3.0 x 10⁸ m/s. This theory of Einstein simply tells us that the formation of the aforementioned fluorine isotope from component subatomic particles is exothermic (heat-releasing). Hence, there must also be the energy associated with breaking down nuclides into their components.

To quantify the binding energy, we need to determine the change in energy (ΔE) and mass (Δm) between the reactants (sum of the mass of individual subatomic particles) and the products (mass of the resulting nuclide). Doing so will change the previous equation to

ΔE = (Δm)c²

Δm can then be calculated as follows:

Δm = mass of products – the mass of reactants

Δm = 3.1548 x 10^-23 g – 3.180288 x 10^-23 g

Δm = – 2.5488 x 10^-25 g or – 2.5488 x 10^-22 kg

Remember that since the atomic mass of the resulting nuclide is always lower than the calculated atomic mass, Δm will always be negative. This means that ΔE is also negative. Substituting the calculated Δm = – 2.5488 x 10^-22 kg and the speed of light constant, c = 3.0 x 10⁸ m/s to Einstein’s equation, we will have:

ΔE = (Δm)c²

ΔE = (– 2.5488 x 10^-22 kg)(3.0 x 10⁸ m/s)²

ΔE = – 2.294 x 10^-5 kg m²/s²

Since 1 J = 1 kg m²/s², then ΔE = – 2.294 x 10^-5 J, and this is the energy released when the aforementioned fluoride isotope is formed from 9 protons and 10 neutrons. In other words, the binding energy of the fluoride isotope is  2.294 x 10^-5 J!

You might ask, why did we omit the negative sign of energy from our calculations?

Remember that the positive and negative signs of energy are simply conventions used by scientists. A negative sign means that the system has given off energy (usually heat), while a positive sign indicates that the system has absorbed energy. This is where it gets tricky! Keep in mind that what we’ve calculated above is the amount of energy released (hence the negative sign) when the fluoride isotope is formed from its elementary components, 9 protons and 10 neutrons.

By definition, the binding energy is required to break down a nucleus into its components: neutrons and protons. The keyword here is “formed” and “break down,” which are opposite processes. If the formation of fluoride isotope is energy-releasing, then the opposite process must be energy-requiring. As a result, the binding energy is assigned with the same magnitude of energy but the opposite sign.

Binding energy is a useful tool in determining atomic stability. The problem with it is that each nuclide has a different number of nucleons in it. To overcome this, the binding energy is often converted to nuclear binding energy per nucleon, simply the ratio of the nuclear binding energy and the number of nucleons. In mathematical form, 

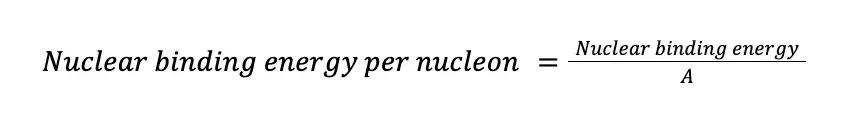
If we apply this equation to the fluoride isotope:

FUN FACT! Physicists and chemists seldom use grams and kilograms as a unit of atomic mass. Instead, they use atomic mass units (amu, or u in some references). To date, the most acceptable conversion factor is 1 amu = 1.66053886(28) x 10^-27 kg!

Nuclear Fission and Fusion

Nuclear fission is a process in which nuclei (typically those with a mass number greater than 200) divide to form relatively lighter nuclei. Because this process forms stable, low-energy nuclides (called daughter nuclides) from highly energetic nuclides (called parent nuclides), the process gives off a huge amount of energy!

One of the most studied nuclear fission reactions is the bombardment of U-235 with a slow-moving neutron as shown below.

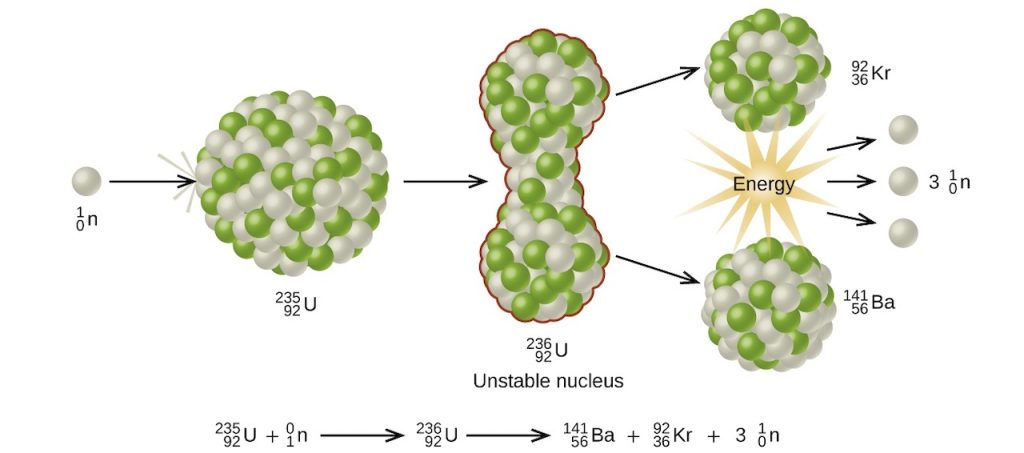
Aside from the enormous amount of energy that this reaction liberates, it produces more neutrons than what was captured in the process. Hence, a nuclear chain reaction is possible. It means that the neutrons generated from the initial stages of nuclear fission can trigger a series of fission reactions in other U-235 nuclides, making them self-sustaining.

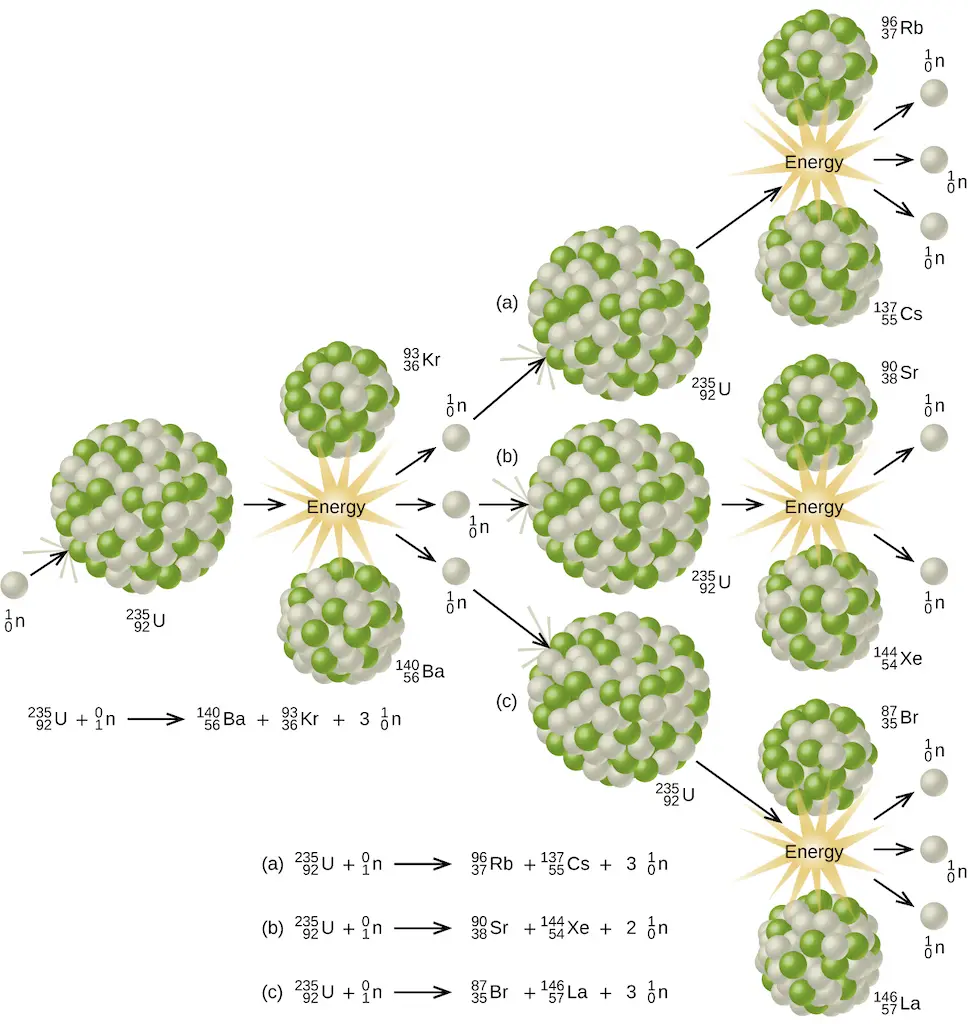
However, there is a minimum amount of parent nuclide necessary for the reaction to become sustainable. This threshold quantity is known as the critical mass. When this criterion is met, the reaction produces a tremendous amount of heat in just a second. In nuclear power plants, especially those with water-based (light-water or pressurized-water) reactors, this energy is used to produce steam which drives the heat turbine, generating electricity. This way, steam can be produced without any CO₂ emitted to the environment!

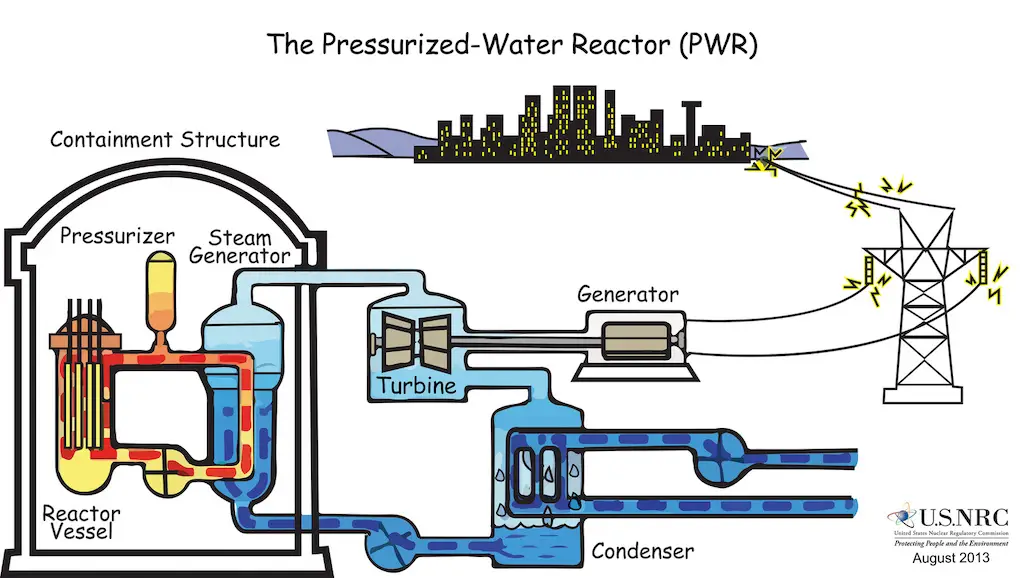
The drawback, however, is the waste generated from the reaction. Usually, fission products are radioactive, highly toxic, and with a long half-life. For instance, Plutonium-239, a nuclear fission product, is one of the most toxic substances, and its half-life is 24,400 years! 

Another problem with nuclear energy is when used as a weapon. The first application of nuclear fission is on the development of atomic bombs! The energy generated is so enormous that a kilogram of U-235 can liberate 8 x 10¹³ J of energy. To put it into perspective, 20,000 tons of trinitrotoluene (TNT) is required to liberate 8 x 10¹³ J!

Nuclear fusion, on the other hand, is a process in which lighter parent nuclides combine to form heavier daughter nuclides. In terms of waste generation, fusion reactions produce significantly fewer hazardous products. However, the reaction requires extremely high temperatures, often called thermonuclear reactions. Stars, including our one and only Sun, generate their energy through nuclear fusion reactions. 

The following reactions are believed to be responsible for providing energy to the Sun and maintaining its interior temperature at approximately 15 million °C:

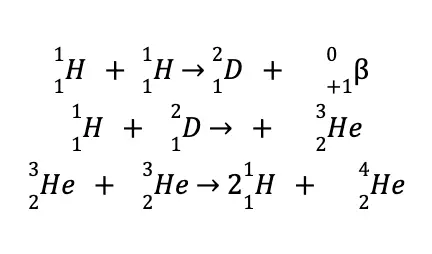
Nuclear fusion is a very promising source of energy, not only due to “cleaner” waste products but also to cheap and almost inexhaustible fuel, as the world’s reserve of deuterium is estimated at 5.0 x 10¹⁵ tons!

Unfortunately, no solid on Earth is known to withstand temperatures of a hundred million degrees Celsius. However, attempts to create a hydrogen bomb (aka thermonuclear bomb) are successful, as it contains tightly packed lithium deuteride instead of gaseous hydrogen or deuterium. This instance overcomes the major limitation encountered in creating nuclear fusion reactors. 

Detonation of hydrogen bombs leads to the following reactions, which are accompanied by the generation of a huge amount of energy.

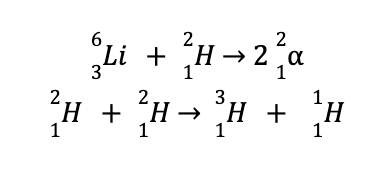
References

Chang R. (2010). Chemistry. 10th ed. McGraw-Hill Companies, Inc. NY: USA.

Young HD, Freedman RA. 2008. Sear’s and Zemansky’s university physics with modern physics. 12th ed. New York, USA: Pearson Education, Inc.

Next topic: Introduction to Relativity

Previous topic: Heat and Thermodynamics

Return to the main article: The Ultimate Physics Reviewer

Download Article in PDF Format

Test Yourself!

1. Practice Questions [PDF Download]

2. Answer Key [PDF Download]