One of the criteria that scientists use to assess the probability of life on other planets is the presence of a habitable atmosphere. Lucky for us, the Earth’s atmosphere is one in a million (if not billion), that’s why we’re able to live on what we call the blue planet.

An atmosphere is defined as the layers of gases that surround any planet in general. Here on Earth, the composition of our troposphere (lowermost layer of the atmosphere) is most suitable for supporting life. In this module, we will tackle the third state of matter, gases, and the laws governing their behavior.

Click below to go to the main reviewers:

Ultimate UPCAT Reviewer

Ultimate NMAT Reviewer

Ultimate LET Reviewer

Table of Contents

• The Concept of Ideal Gas
• Empirical Gas Laws
  • 1. Boyle’s Law
  • 2. Charles’s and Gay-Lussac’s Law
  • 3. Avogadro’s Law
  • 4. Combined Gas Law
• Ideal Gas Equation
• References
• Download Article in PDF Format
• Test Yourself!
  • 1. Practice Questions [PDF Download]
  • 2. Answer Key [PDF Download]

The Concept of Ideal Gas

Let us do an experiment first before we discuss this topic.

Put your palm near your mouth, and with your mouth wide open, try to blow some air towards your palm. How does it feel? Does it feel hot or cold? Next, try to pout, and again, with your palm near your mouth, blow some air into it. How does it feel now? It feels colder, right?

This phenomenon is called the Joule-Thomson expansion; your breath feels cooler as it passes through a smaller exit because the air in your breath behaves like a real gas. If your breath behaves as an ideal gas, there will be no difference in the temperature of the gas between the two scenarios that we did.

For a gaseous system to become ideal, there are four conditions that must be satisfied first, and these are the following:

1. The gas particles have negligible volume.
2. The gas particles are equally sized and do not interact with neighboring gas particles.
3. The gas moves in a random motion.
4. Collisions between gas particles are perfectly elastic.

As you can see from these assumptions, it is almost impossible to have an ideal (or perfect) gas, right? That’s true, but we can “force” the gas to behave ideally under low-pressure and high-temperature conditions.

Low pressure means that the gas occupies a large volume, and high temperature provides high kinetic energy to gas molecules, which can minimize the interactive forces between gas molecules. Furthermore, the use of gases with low molar mass (such as H₂ gas) can further promote ideal behavior. In this section, we will deal with equations that describe the properties of ideal gases.

Empirical Gas Laws

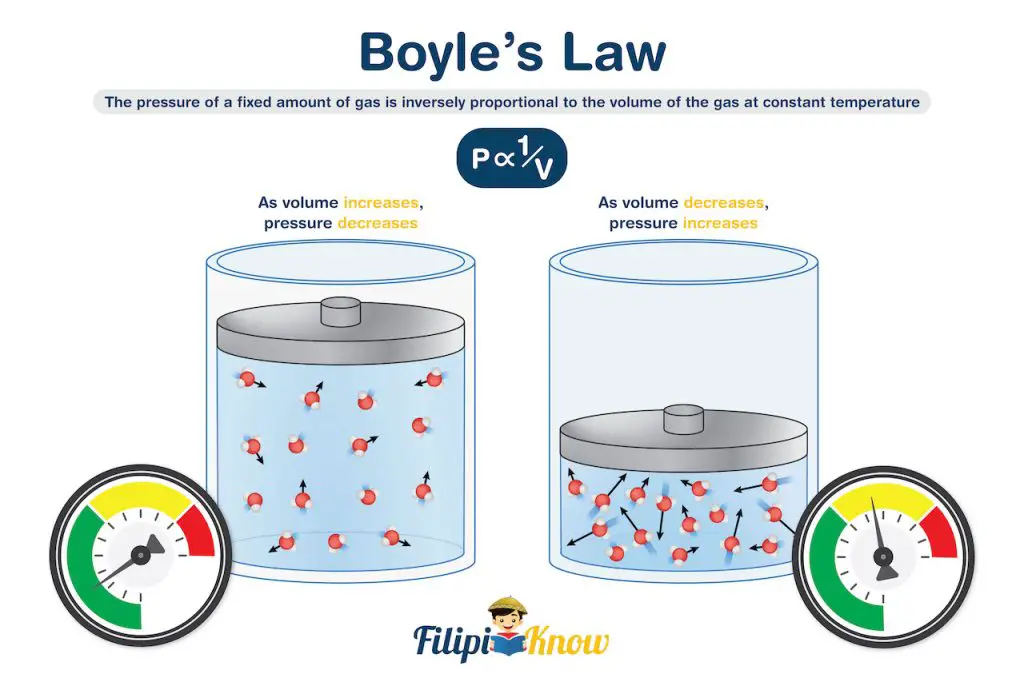
1. Boyle’s Law

When you were a child, did you also try to push the plunger of a needleless syringe while sealing the exit with your finger? Back then, my goal was to push the plunger to the tip of the syringe, not knowing that there was air inside which prevented me from doing so.

Fast forward to my high school days, during my Chemistry class, I recalled this experiment and realized, “AHA, it’s Boyle’s Law!”

Boyle’s law relates the pressure and volume of an ideal gas under constant temperature. It states that at a constant temperature, the pressure of a fixed amount of gas is inversely proportional to the volume of the gas.

If you also did the syringe experiment, try to recall that the plunger becomes harder to push as the tip of the plunger approaches the tip of the syringe. This is because pushing the syringe further decreases the volume occupied by the gas, which results in an increased pressure exerted by the gas towards the plunger.

Quite amazing, right? We didn’t know that at such a young age, we had already demonstrated Boyle’s law!

Although we demonstrated it using a syringe, Robert Boyle, a British chemist and natural philosopher, demonstrated this phenomenon in the 17th century using a bent glass tube and mercury. By virtue of this law, it can be said that for a given sample of gas under two different sets of conditions, the relationship between its pressure and volume before and after the change is given as

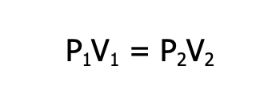
where P is the pressure, and V is the volume of the gas under the two different sets of conditions. Keep in mind that this formula is valid only under constant temperature and as long as the amount of the gas does not change.

MNEMONIC: Boyle’s Law is the first of the numerous gas laws you will encounter. To easily recall what parameter is constant in Boyle’s law, just remember BOYLET (Boyle’s Law, constant T!)

Sample Problem:

A sample of oxygen gas exerts a pressure of 2.50 atm in a 20.0 L container. What will be the new pressure it will exert if all of it will be transferred to a 16.0 L container at constant temperature? Assume that the gas behaves ideally.

Solution:

Initially, the volume occupied by the gas is 20 L and exerts a pressure of 2.50 atm. Since the temperature and the amount of gas are constant, and the gas was assumed to behave ideally, we can use Boyle’s law to solve the new pressure after it was transferred to a 16 L container.

Therefore, the new pressure is 3.125 atm.

2. Charles’s and Gay-Lussac’s Law

After Robert Boyle successfully established the relationship between volume and pressure in gases, one question arose:

Why does the pressure-volume relationship hold true only at constant temperature?

This was answered in the early 19th century by the separate work of Jacques Alexandre Cesar Charles and Joseph Louis Gay-Lussac. Their studies showed that at constant pressure, there exists a linear relationship between temperature and the volume of gases. This means that a certain amount of gas expands when heated and contracts when cooled. Their separate work led to the development of Charles’s and Gay-Lussac’s law or simply Charles’s law, which states that the volume of a fixed amount of gas maintained at constant pressure is directly proportional to the absolute temperature of the gas.

The mathematical expression of Charles’ law will lead to the derived equation

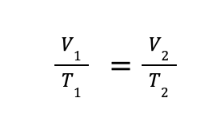
where V₁ and T₁ are the initial volume and temperature, while V₂ and T₂ are the final volume and temperature, respectively.

When working with temperatures in gas laws, make sure that the temperature is always on the Kelvin scale, as it was clearly stated in the law that the proportionality was associated with the absolute temperature of the gas. Use the formula below to convert temperatures in ℃ to Kelvin.

T (in K) = T (in ℃) + 273

This observation can be explained by the expansion of the gas. As the temperature increases, the kinetic energy of gas molecules increases, which causes the gas to exert more pressure against the container. However, since the pressure is constant, the increase in pressure applied by the gas is manifested as an increase in the volume occupied by the gas.

What if we let the expanding gas exert more pressure on its container while keeping the volume occupied by the gas constant? Doing so will lead us to the alternative form of Charles’s law, which some references call Gay-Lussac’s or Amonton’s law. This relates the pressure and temperature of a fixed amount of gas under constant volume conditions and is mathematically expressed as:

where P₁ and T₁ are the initial volume and pressure, while P₂ and T₂ are the final volume and pressure, respectively.

MNEMONICS: To avoid confusion on which property is constant, you can just remember CHARLEP (Charles’ Law, constant Pressure).

3. Avogadro’s Law

Now, what if we add a certain amount of gas to the system at constant temperature and pressure? What do you think will happen?

In this respect, let’s just say that ideal gases are like your clothes. When you have so many clothes that they don’t fit your wardrobe anymore, normally, you (although most probably, it will be your mother) transfer your clothes to a larger wardrobe, right?

The same is true for ideal gases. If you increase the amount of gas under constant temperature and pressure conditions, the tendency of the gas is to increase its volume. This is known as Avogadro’s law, named after Italian chemist Lorenzo Romano Amedeo Carlo Avogadro.

Avogadro’s law states that at constant temperature and pressure, the volume of a gas is directly proportional to the number of moles of gas present. The mathematical expression of Avogadro’s law will lead to the derived equation.

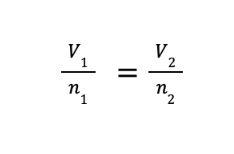
where V₁ and n₁ are the initial volume and number of moles, while V₂ and n₂ are the final volume and number of moles, respectively.

Sample Problem:

What amount of an ideal gas must be added to double the volume occupied by the same gas with an initial amount of 0.25 moles under constant temperature and pressure?

Solution:

Since the system is subjected to constant temperature and pressure, we can use Avogadro’s law to solve this problem. However, we are not given the initial volume. For such cases, we can use arbitrary volume.

We want to compute the amount of gas that needs to be added so that the volume will be doubled. Hence, if we arbitrarily select V₁ = 1.0 L, then V₂ = 2.0 L. We are given the n₁, hence, we can already solve the problem.

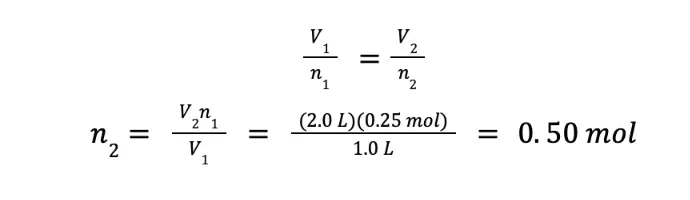
Although we got 0.50 mol as the final answer, this number does not answer our question. We were asked what amount of the gas must be added to double the volume that the gas will occupy. Initially, there’s 0.25 mol of gas. To double the volume, the amount of the resulting gas should be 0.50 mol. Hence, we need to add 0.25 mol of the same gas to the system.

4. Combined Gas Law

So far, we have considered cases wherein two variables are always constant. However, there are cases wherein the volume, temperature, and pressure all change at the same time. In such cases, the combined gas law can be used.

The combined gas law was obtained by combining Boyle’s law, Charles’ law, and Amonton’s law. This law expresses the relationship between the volume, pressure, and absolute temperature of a fixed amount of gas. The mathematical expression of the combined gas law will lead to the derived equation shown below.

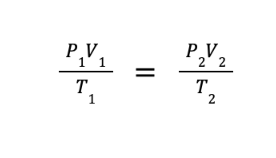
Sample Problem:

A fixed amount of an ideal gas is compressed to half of its original volume. If initially, the gas exerts 1.5 atm at a temperature of 300 K, what would be the ratio of final temperature over the final volume after compression if the pressure becomes 2.0 atm?

Solution:

It was stated that only the amount of gas is constant. Hence, we should use the combined gas law.

Since the gas is being compressed to half of its initial volume, and there is no initial volume given, then we can assign arbitrary values. For simplicity, we let V₁ = 2.0 L and V₂ = 1.0 L. Furthermore, P₁ = 1.5 atm, T₁ = 300 K, and P₂ = 2.0 atm.

Using the combined gas law:

What we have so far is the ratio of the final volume over the final temperature. However, we are asked to determine the ratio of the final temperature over the final volume. We can get this by getting the reciprocal of the equation above, which gives us

Ideal Gas Equation

The ideal gas equation accounts for the behavior of all ideal gas. This equation relates the pressure, absolute temperature, volume, and amount of the gas. This means that if we know three out of four properties of the gas, then we can compute the missing property using the ideal gas equation.

The mathematical expression of the ideal gas expression is shown below:

PV = nRT

R is known as the universal gas constant, which is equal to 0.0821 L⦁atm/mol⦁K, or  8.314 J/mol⦁K

IMPORTANT NOTE: A mole of ideal gases, regardless of identity, occupies a molar volume of 22.414 L at 273.15 K (or 0 ℃) with a pressure of 1 atm. This temperature and pressure condition is known as the standard temperature and pressure (STP). Another benchmark condition is the standard ambient temperature and pressure (SATP). At SATP, the temperature is 298.15 K (or 25 ℃), and the pressure is 1 bar.

Sample Problem:

Write an expression that will allow us to determine the volume occupied by 0.67 mol SF₆ (146 g/mol) at SATP if it behaves as an ideal gas.

Solution:

We need to use the ideal gas equation to be able to address this problem. To easily visualize the problem, let us first list what is known.

• R = 0.0821 L⦁atm/mol⦁K
• n = 0.67 mol
• T = 298.15 K
• P = 1 bar

Remember that we are asked to write an expression that will enable us to solve the volume of the gas. Hence, the units of the given that we need to use should cancel each other out.

If we use R = 0.0821 L⦁atm/mol⦁K, this means that the unit of the amount should be in mole, the unit of temperature should be in Kelvin (K), and the unit of pressure should be in atmosphere (atm). That being said, we need to convert 1 bar to atm first. We know that 1 atm = 1.01325 bar. Therefore:

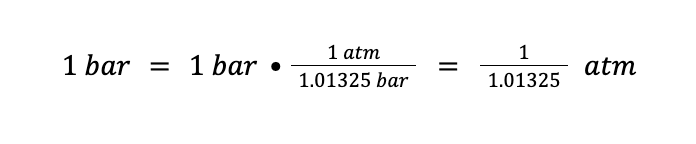
Then, from the ideal gas equation:

References

Chang, R. (2010). Chemistry (10th ed.). New York City, USA: McGraw-Hill Companies, Inc.

Gay-Lussac’s Law. (2022). Retrieved 17 June 2022, from https://chem.libretexts.org/Bookshelves/Introductory_Chemistry/Book%3A_Introductory_Chemistry_(CK-12)/14%3A_The_Behavior_of_Gases/14.05%3A_Gay-Lussac’s_Law

Kotz, J. (2022). Chemistry and Chemical Reactivity. Stamford, CT: Cengage Learning.

Silberberg, M. (2006). Chemistry: The molecular nature of matter and change (4th ed.). New York City, USA: McGraw-Hill Companies, Inc.

Zumdahl, S., Zumdahl, S., & DeCoste, D. (2010). Chemistry (8th ed.). Belmont, California: Brooks Cole.

Next topic: Chemical Reactions

Previous topic: Compounds

Return to the main article: The Ultimate Chemistry Reviewer

Download Article in PDF Format

Test Yourself!

1. Practice Questions [PDF Download]

2. Answer Key [PDF Download]