Speed limits are set to ensure drivers’ safety. 

Using speed and laser guns, the authorities can track vehicles and their speed to ensure that no violations of speed limit regulation happen.

Laser guns are instruments that use laser beams to calculate the round-trip time for light to penetrate and bounce back into a vehicle. These devices can measure the distance traveled as well as the speed of the vehicles.

The science of laser speed guns is an example of kinematics – the study of motion.

In this reviewer, we are going to discuss kinematics, specifically the motion of objects in one and two dimensions. Our focus will be on how to solve problems using kinematic equations.

Click below to go to the main reviewers:

Ultimate UPCAT Reviewer

Ultimate NMAT Reviewer

Ultimate LET Reviewer

Table of Contents

• Horizontal Motion with Constant Acceleration
• Vertical Motion with Constant Acceleration
• Projectile Motion
• Download Article in PDF Format
• Test Yourself!
  • 1. Practice Questions [PDF Download]
  • 2. Answer Key [PDF Download]

Horizontal Motion with Constant Acceleration

The kinematic equations include variables such as displacement, velocity, acceleration, and time. 

In kinematics, note that acceleration will always have a constant value since we would not be looking at forces that cause acceleration to change over time, while displacement and velocity could have an initial or final value.

The following are the fundamental kinematic equations:

To solve problems that involve kinematic equations, remember to follow the tips below.

1. Read and understand the problem, the given quantities, and what quantity is being asked.
2. Choose the appropriate equation.
3. Plug in the values and solve the problem.

Let us try to solve some problems.

Sample Problem:

A cheetah that moves in a constant acceleration covers the distance between two points 50.0 m apart in 5.00 s. Its speed is 15.0 m/s as it reaches the second point. 

a. Find its speed as it passes the first point.

b. What is the cheetah’s acceleration?

Solution:

To solve this problem easier, we must list down all the given quantities first and determine which quantities we must calculate.

The distance between the two points is 50.0 m, so

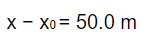
The time it took to cover this distance is 5.00 s, so

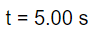
Lastly, the cheetah’s speed as it reaches the second point is 15.0 m/s, so the final speed

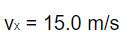
a. We are looking for the cheetah’s initial speed, so we are going to use the equation 

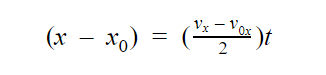
Substituting the values and calculating the initial speed, we will get

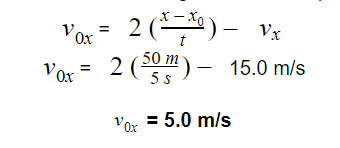
b. Since we are looking for the cheetah’s acceleration, we are going to use the equation

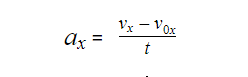
Calculating for acceleration, we will get

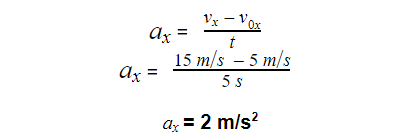
Vertical Motion with Constant Acceleration

The most familiar example of motion with constant acceleration is a body falling under the influence of the earth’s gravitational attraction. Such a special case of one-dimensional motion is known as free fall.

In free fall, the constant acceleration is due to gravity. An object that undergoes free fall has an acceleration of 9.8 m/s² downward (on Earth). This value is commonly known as acceleration due to gravity – the value of an object’s acceleration moving under the influence of gravity. It is denoted by the symbol g.

We have applied the kinematic equations for horizontal motion. This is just the same as the vertical motion. The only difference is that the value of acceleration will be the acceleration due to Earth’s gravity or -9.8m/s².

Note that the negative direction will always be downward, and objects will always accelerate towards the Earth. See the equations below.

Sample Problem 1: Object being dropped

Suppose you drop a stone off a 350-meter cliff. 

a. How long was the stone in the air?

b. How fast will it travel when it lands?

Solution:

To solve this problem easier, we must list down all the given quantities first and determine which quantities we must calculate.

The distance between the two points is 350 m, so y − y₀ = -350 m (negative since the stone travels downwards), while the initial velocity v_0y is 0 because the stone was dropped from rest. 

a. To calculate the time, we are going to use the equation

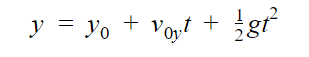
Since  v_0y is 0,

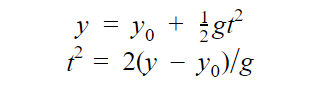
Substituting the values, we will get

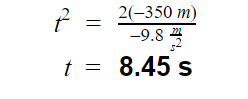
b. Since we are looking for its velocity upon impact, we are going to use the equation

Calculating for velocity, we will get

Sample Problem 2: Object being thrown upward

Suppose you throw the same stone upward with an initial velocity of 2 m/s.

a. How long was the stone in the air?

b. How fast is it going when it hits the ground? 

Solution:

We are now given an initial velocity v_0y of 2 m/s.  

a. To calculate the time, we are going to use the equation

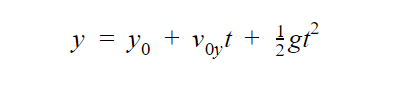
Substituting the values, we will get

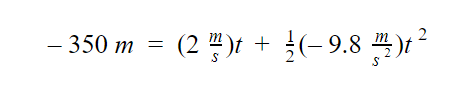
Using the quadratic equation,

Note: There are two values for a time, but we will only get the positive value since time cannot be negative.

b. Since we are looking for its velocity upon hitting the ground, we are going to use the equation

Calculating for velocity, we will get

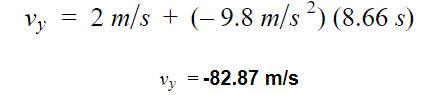
Projectile Motion

We have already discussed using kinematic equations for objects that move in the horizontal and the vertical direction, but what if the objects move in both directions?

The type of motion that involves an object that is thrown or launched in the air is called projectile motion.

Any object that has an initial velocity and follows a path determined by the effects of gravitational acceleration and air resistance is called a projectile. The path that is followed by a projectile is called a trajectory. 

Do you still remember playing shatong? That is a good example of projectile motion.

You throw the stick at some angle from the horizontal. Before reaching the ground some distance away from its origin, it will travel at some distance up into the air first.

To describe the path of the stick, we can use a parabola.

The key to solving this kind of problem is to take note that the horizontal and vertical motion of the stick is independent of one another. Hence, we can use separate equations to determine the motion in each direction.

Sample Problem:

You throw a stone with an initial velocity of 4.7 m/s at an upward angle of 60 degrees off horizontal from the edge of a 350-meter cliff. 

a. How long is the stone in the air?

b. How far from the cliff will the stone land?

Solution.:

First, let us distinguish the horizontal and vertical motion.

The time the stone spends in the air solely depends on the vertical motion because it will only stop being in the air when it hits the ground. The stone will be in the air regardless of the horizontal velocity.

However, the distance traveled by the stone depends on both horizontal and vertical motion.

Velocity can also be split into components. The horizontal velocity of the rock will be constant (neglecting air resistance) while the vertical velocity is at its maximum the moment the stone is thrown, continuously decreasing until it reaches zero (maximum height) and then increasing negatively until it reaches the ground. 

To find the horizontal and vertical velocity of the stone, we can use trigonometric functions. 

Vx = 4.7 cos 60 = 2.35 m/s

Vy = 4.7 sin 60 = 4.07 m/s

These velocities are independent of one another. A stone that is thrown with an initial velocity of 4.07 m/s will land on the ground at the same time as a stone that is thrown at 4.7 m/s at 60 degrees.

Therefore, we can solve for the time by applying what we have learned in a linear vertical motion. 

a. To calculate the time, we are going to use the equation

Substituting the values and calculating for the t, we will get

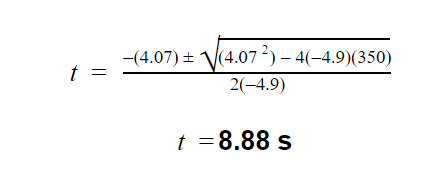
b. Since we are looking for the distance, we can just use the equation 

d = v_xt

Calculating the distance, we will get

d = (2.35 m/s) (8.88 s)

d = 20.87 m

The stone is 20.87 meters away from the edge of the cliff. 

Next topic: Relative Velocities

Previous topic: Scalar and Vector Quantities

Return to the main article: The Ultimate Physics Reviewer

Download Article in PDF Format

Test Yourself!

1. Practice Questions [PDF Download]

2. Answer Key [PDF Download]