We all know that physics can explain a lot of amazing things that happen from a subatomic point of view to vast outer space. But before we go into all that, we must first understand a few topics such as the unit of measurement, scientific notation, and dimensional analysis.

Aside from these topics, one other prerequisite in studying physics is the understanding of scalars and vectors.

Click below to go to the main reviewers:

Ultimate UPCAT Reviewer

Ultimate NMAT Reviewer

Ultimate LET Reviewer

Table of Contents

• What Are Scalars and Vectors?
• Vector Addition
• Vector Subtraction
• Unit Vector
• Components of Vectors
• Vector Sum
• Download Article in PDF Format
• Test Yourself!
  • 1. Practice Questions [PDF Download]
  • 2. Answer Key [PDF Download]

 

What Are Scalars and Vectors?

Scalars are quantities that have magnitude. These can be the temperature in your room, the amount of time you spend reading this reviewer, or even the mass of your laptop.

Scalars are often represented by a letter and are all numerical quantities that only answer the question, “How much?”

On the other hand, vectors are quantities that have magnitude and direction. In studying physics, these are important because we need these to understand other physics topics such as force.

When we study force, we do not only look at how much force is being applied but also in what direction. These respond to the questions, “How much?” and “Which way?”

Vectors are also represented by an arrow where the length of the arrow corresponds to the vector’s magnitude, the tail represents the origin of the vector, and the arrowhead indicates the direction of the vector.        

As we study physics, we must predict the motion of objects. To do so, we should be knowledgeable of operations involving vectors.  

 

Vector Addition

To add two vectors, connect the second vector’s tail to the first vector’s arrowhead, then draw a resultant vector from the tail of the first vector to the head of the second vector.

Take note that the direction of the vectors must be retained. If two vectors will be added in the same direction, the vector sum will just be a longer vector.

When two vectors to be added are perpendicular, the magnitude of the vector sum can be calculated using the Pythagorean theorem and trigonometric functions.

Sample Problem:

Joshua wants to go to school. From his house, he walks 3 meters to the East and then heads 4 meters to the North. Which path should he take to get there faster?

Solution:

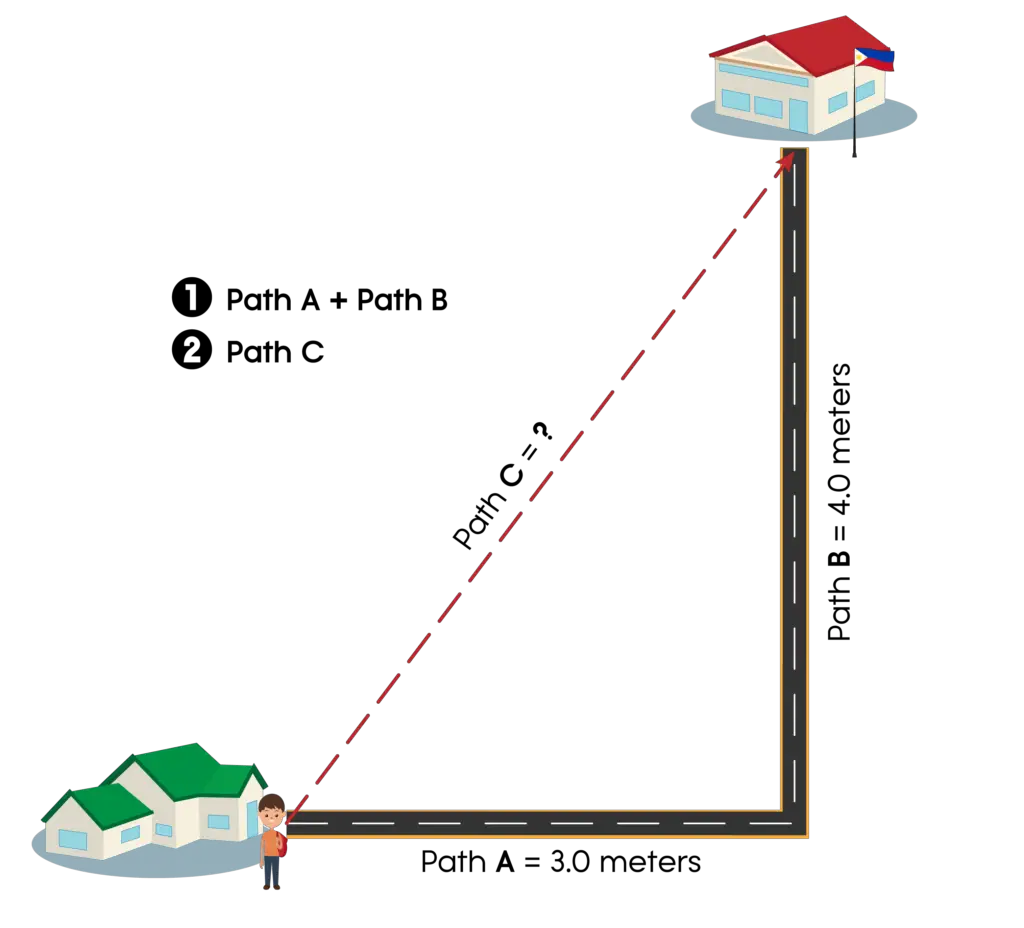
We can notice that the second path Joshua has crossed is perpendicular to the first path. If we draw a line from Joshua’s house to his school, a right triangle is formed. In this case, we are going to use the Pythagorean theorem.

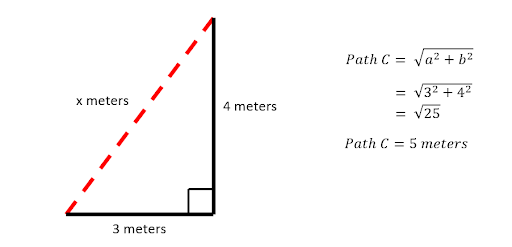
Hence, Joshua’s house is 5 meters away from his school. He can take the second path to go to school faster.

The sum of all paths taken is known as distance, while the difference between the final position and the initial position is called displacement.

Displacement is a vector quantity because it needs to know the change in direction, while distance is a scalar quantity because it is only concerned with the total amount of path traveled regardless of the direction.

 

Vector Subtraction

This is like vector addition, except what we are going to do is invert the direction of the second vector (see image below). This is also the same as the vector being multiplied to a scalar of -1. This way, the magnitude of the vector remains the same, but the direction is the opposite, so we have A-B, which is pretty much the same as A+ (-B).

 

Unit Vector

A unit vector is a dimensionless vector used to describe a direction in space. It does not have units and has a magnitude of 1.

For many expressions, especially in the components of vectors, this is used as a notation. This is often denoted using a caret or hat (^).

Axes	Unit Vectors	Coordinates
x	î	(1, 0, 0)
y	ĵ	(0, 1, 0)
z	k̂	(0, 0, 1)

This can also be used to calculate the magnitude of a vector. The vector magnitude can be calculated using the formula below.  

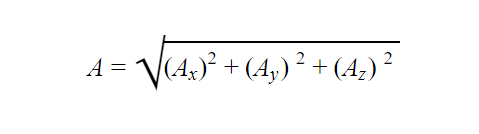
Check the example below (zoom in the image if you’re unable to see it clearly):

 

Components of Vectors

The vector component implies the parts of a vector – the x-component and the y-component.

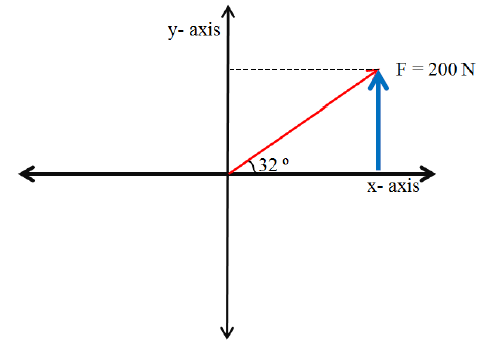
Study the force vector below.

Given above is a set of axes (x and y) with a force vector of 200 N in the direction of 32 º North of East. This force vector has an x-component and a y-component.

1. Getting the x–component. To get the x-component of the vector, draw a  vertical broken line from the end of the vector to the x-axis. Then starting from the origin, draw a vector along the x-axis up to the tip of the vertical line. The dark green line on the figure below represents the x – component of the force vector.

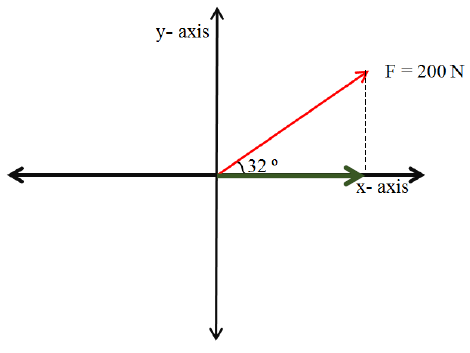
2. Getting the y–component. To get the y-component of the vector, draw a horizontal broken line from the y-axis to the end of the force vector. Draw a vertical vector parallel to the y-axis starting from the x-axis to the end of the force vector. The blue line on the figure below represents the y – component of the force vector.

 

Vector Sum

To calculate this, the components of the added vectors will be used (more details below).

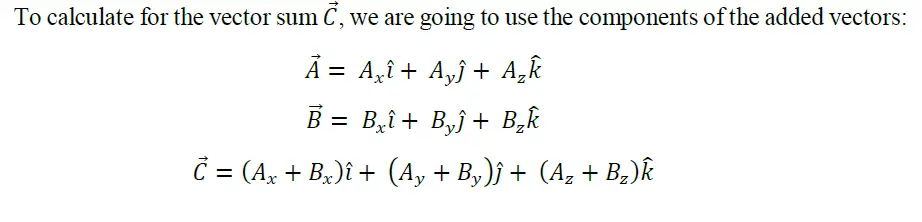
Sample Problem:

After class, Kai wants to go to the grocery store. The map below shows the paths he has to take to get there.

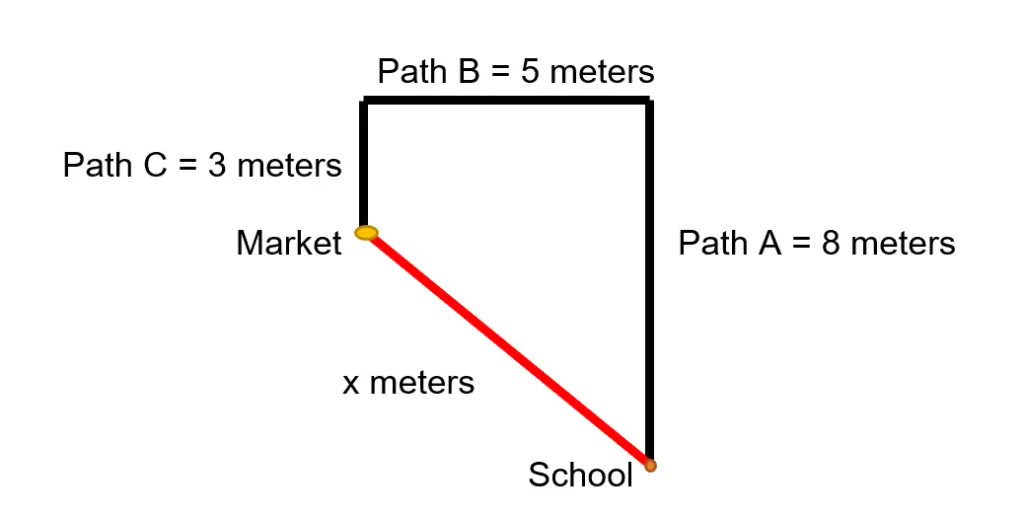
Find how far the grocery store is from Kai’s school and its direction. 

Solution:

We are looking for Kai’s displacement. First, we are going to calculate the components of the vectors.

Using the components of adding vectors,

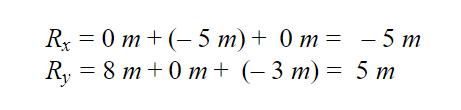
To find how far the grocery store is from school, we must calculate the magnitude of the resultant vector.

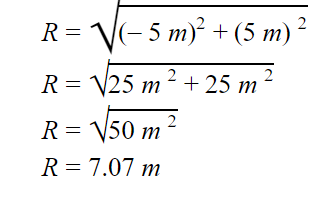
To find the direction, we are going to use some trigonometric functions.

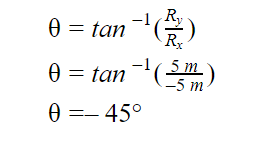
Final Answer: The grocery store is 7.07 meters away from Kai’s school and is 45° North of West.

 

Next topic: Kinematics

Return to the main article: The Ultimate Physics Reviewer

 

Download Article in PDF Format

Test Yourself!

1. Practice Questions [PDF Download]

2. Answer Key [PDF Download]