Linear Inequalities Examples and Answers

Equality, balance, and symmetry may be our ideal conditions for everything. However, mathematics tells us that not everything is within equality.
A lot of things around us don’t exhibit equality in quantities. Sometimes one quantity is greater than or less than the other. For instance, your parent’s age is greater than yours, a dog’s height is less than a tree’s height, or the number of participants in an event is greater than the total seats in the stadium.
Inequality surrounds us; just like equations, they are fascinating to learn and analyze.
Click below to go to the main reviewers:
Ultimate Civil Service Exam Reviewer
Ultimate PMA Entrance Exam Reviewer
Ultimate PNP Entrance Exam Reviewer
Table of Contents
What Is Inequality in Mathematics?
Inequality tells us that the value of one quantity is not the same as the other.
If two quantities are not of the same value, either the value of one quantity is greater than or less than the other.
For instance, 5 > 3 tells us that 5 and 3 are not of the same value since 5 is greater than 3.
Five symbols are usually used to indicate inequality:
- the less than sign (<)
- the greater than sign (>)
- the greater than or equal sign (≥)
- the less than or equal sign (≤)
- the unequal sign (≠)
These symbols are called inequality signs.
We also use variables to represent a certain quantity in an inequality. For instance, x > 5 tells us that a particular number, x, has a value greater than 5. Some possible values of x are 6, 7, 8, 9, and so on.
Just like equations, an inequality has two sides: the left-hand side and the right-hand side. The left side consists of quantities on the left of the inequality sign, while the right side consists of quantities on the right.
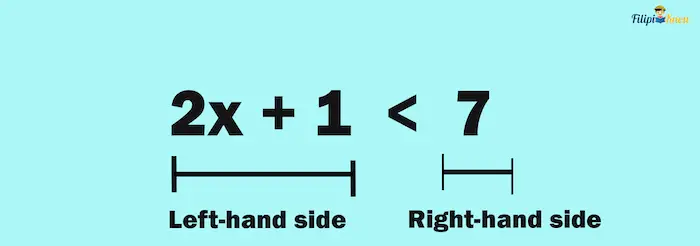
The Solution to Inequality
The solution to inequality is a set of numbers that satisfies the given inequality. That is, when you substitute a number from that set, it will make the inequality hold.
Suppose the inequality x + 1 > 10.
Note that x = 12 is a solution to the inequality since if we plug x = 12 into the inequality, the result will be true:
(12) + 1 > 10
13 > 10 TRUE
Furthermore, x = 15 is also a solution since:
x + 1 > 10
(15) + 1 > 10
16 > 10 TRUE
Also, x = 100 is a solution since:
x + 1 > 10
(100) + 1 > 10
101 > 10 TRUE
There are a lot of possible values of x that will satisfy the inequality x + 1 > 10. However, when solving an inequality, we do not list all these possible values of x (since it will take us forever to do so!).
For this reason, we want to write the solution to inequality as a set of all possible numbers that satisfy the inequality. In short, the solution to inequality is not a single number but a set of numbers. We call this set the solution set of the inequality.
Going back to our example, x + 1 > 10. The solution to this inequality is x > 9.
x > 9 pertains to all numbers greater than 9. Hence, the solution to the inequality x + 1 > 10 is the set of all numbers greater than 9.
If you try x = 8 and substitute it with x + 1 > 10:
(8) + 1 > 10
9 > 10 FALSE
x = 8 is not part of the solution to the inequality since it makes the inequality false. Furthermore, eight is not included in the solution set x > 9.
You might be wondering how I can solve the solution set of the inequality x + 1 > 10. Don’t worry because we will be discussing it later in this review.
Properties of Inequality
These properties will help solve inequalities. If you still remember the properties of equality, then learning the properties below will be easier, as the two have some similarities.
1. Trichotomy Property of Inequality
Given real numbers a and b, only one of the following is true: a > b, a < b, or a = b
This property tells us that a quantity is either larger than the other, smaller than the other, or equal to the other. It is mathematically impossible for two of these conditions to happen at once.
For instance, if your friend tells you that his pocket money is less than ₱1000, it means that his money is neither greater than ₱1000 nor equal to ₱1000.
2. Reversal Property of Inequality
If a > b, then b < a (also applies with <, ≥, and ≤)
This states that if we interchange the quantities on the left-hand and right-hand sides of the inequality, the sign of the inequality reverses.
For instance, we know that 5 > 2. Then, if we interchange the positions of 5 and 2, we must reverse the inequality sign to keep the inequality accurate. Thus, by reversal property: 2 < 5.
Another example of the reversal property: If Peter is older than Paul, it also means that Paul is younger than Peter.
Example: Apply the reversal property to the following:
- 9 > -1
- x < y
- a > b
Solution:
- -1 < 9
- y > x
- b < a
3. Addition and Subtraction Property of Inequality (API/SPI)
If a > b, then a + c > b + c. Also, if a > b, then a – c > b – c (also applies with <, ≥ , ≤)
According to this property, if we add or subtract the same number to both sides of the inequality, the inequality will still hold, or the inequality will still be true.
For instance, we know that 3 < 5. Suppose that we add 12 to both sides of the inequality:
3 + 12 < 5 + 12
15 < 17
Notice that the resulting inequality is still valid.
Now, suppose that we subtract 12 from both sides of 3 < 5:
3 – 12 < 5 – 12
-9 < -7
Note that the resulting inequality is still true.
4. Multiplication Property of Inequality (MDI)
If a > b, then ac > bc when c > 0 and ac < bc when c < 0
The multiplication property of inequality tells us that the inequality holds if you multiply both sides of an inequality by the same positive number. However, if you multiply both sides of the inequality by a negative number, the inequality sign is reversed to make the inequality hold.
Suppose 5 > 1, and we want to multiply both sides by 3:
5(3) > 1(3)
15 > 3
Note that the inequality is still valid after multiplying both sides by the same number.
Now, suppose we multiply both sides of 5 > 1 by -3:
5(-3) > 1(-3)
-15 < -3
The inequality sign is reversed so that the resulting inequality is true.
5. Division Property of Inequality (DPI)
If a > b, then a/c > b/c when c > 0 and a/c < b/c when c < 0
The DPI is somehow similar to MPI. If we divide both sides of the inequality with the same positive number, the inequality holds. However, if we divide both sides of the inequality with the same negative number, the inequality sign is reversed to make the inequality hold.
For example, let us divide both sides of the inequality 15 < 20 by 5:
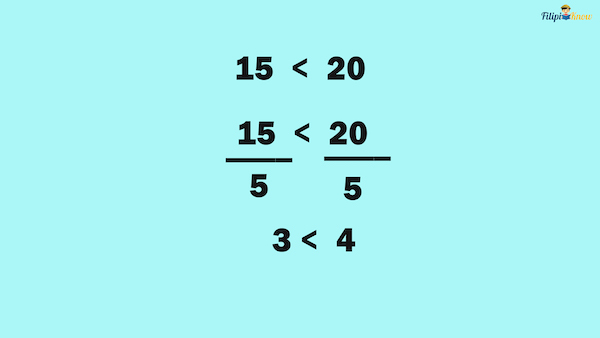
The resulting inequality is still valid after dividing both sides by 5.
On the other hand, if we divide both sides of 15 < 20 by -5:
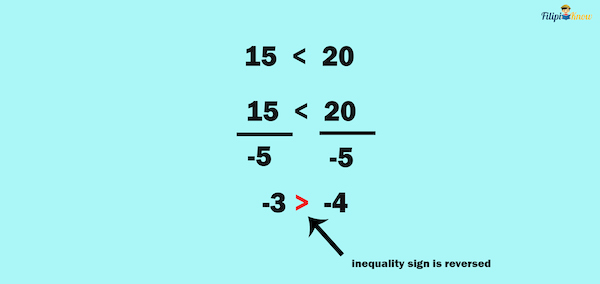
Notice that the inequality sign is reversed so that the resulting inequality will remain valid.
Linear Inequalities in One Variable
The type of inequalities we will solve in this review is linear inequalities in one variable. These are inequalities with only one variable involved, and the exponent of that variable is only 1.
For instance, x – 5 ≤ 0 is a linear inequality in one variable since it has only one variable involved (x), and the exponent of that variable is 1.
Example: Which of the following is a linear inequality in one variable?
a) 2x + 3y > -1
b) 5x – 1 < -8
c) x2 + 3x > -1
Solution: The only linear inequality in one variable is the one in the letter b. It is the only inequality with one variable involved (x) and the exponent of that variable is 1.
How To Solve Linear Inequalities in One Variable
1. Using the Addition and Subtraction Properties of Inequality
To solve linear inequalities in one variable, we have to apply the properties of inequality.
Like with equations, our primary goal in solving a linear inequality is to isolate the variable x from other quantities. This means that one side of the inequality must contain only the variable x, and the other variables must be on the other side.
Let us try to solve x – 4 > 2
To solve for the inequality x – 4 > 2, we need to isolate x from other quantities. This means that x must be the only quantity on the left-hand side of the inequality.
The addition property of inequality allows us to add 4 to both sides of the inequality. Note that if we add 4 to both sides of the inequality, the -4 on the left-hand side will be eliminated, and only x will remain.
x – 4 > 2
x – 4 + 4 > 2 + 4 Addition Property of Inequality
x > 6
That’s it! We have isolated x from other quantities. The solution set of the inequality is x > 6. This means that any number greater than six will satisfy the inequality.
Example: Solve for the inequality x + 9 > 10
Solution: Again, we have to eliminate nine on the left-hand side so that only x will remain. To achieve this, we can subtract nine from both sides of the inequality:
x + 9 > 10
x + 9 – 9 > 10 – 9 Subtraction Property of Inequality
x > 1
Hence, the solution to the inequality is x > 1.
2. Transposition Method in Inequalities
Do you still remember the transposition method?
To refresh your memory, the transposition method is more convenient for isolating a variable from other quantities than adding or subtracting a number on both sides of the equation.
We can also use this method on inequalities. Say we want to solve x + 9 > 10. We aim to isolate x from other variables and make it the only quantity remaining on the left-hand side. We can transpose or move 9 to the right-hand side to accomplish this. However, if 9 crosses the inequality sign, it will be -9 (its sign reverses).
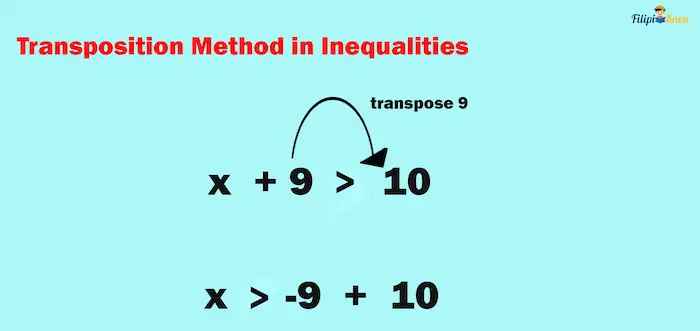
From x + 9 > 10, we have x > -9 + 10 using the transposition method. This leads us to x > 1 as the solution set.
Did you see how convenient it is to use the transposition method rather than adding or subtracting both sides of an inequality by the same number? For this reason, we will be using the transposition method throughout this review when solving inequalities.
Example 1: Solve for the inequality x + 5 > 17 using the transposition method.
Solution: We can transpose 5 to the right-hand side so that x will be the only quantity that will remain on the left-hand side (i.e., isolate x from other quantities). Note that 5 changes to -5 when transposed to the right-hand side.
x + 5 > 17
x > -5 + 17
x > 12
Thus, the solution to the inequality is x > 12 or all real numbers greater than 12.
Example 2: What is the largest whole number that will satisfy x – 5 < 90?
Solution: Rather than a solution, this example asks for the largest number to satisfy the inequality. So, our final answer should be a number and not a set.
But, we need to solve the solution set of the inequality first to determine the largest number that satisfies the inequality.
x – 5 < 90
x < 5 + 90 Transposition Method
x < 95
This tells us that the solution set of the inequality is the set of all numbers less than 95. However, to solve the problem, we must determine the largest whole number in the set x < 95. So, what is the largest whole number less than 95? That number is 94.
Note that 95 is not the largest number in the set x < 95 since 95 is not included.
Therefore, the answer to this example is 94.
Example 3: What is the smallest whole number that will satisfy the inequality x – 12 > 100?
Solution: Let us solve for the solution set first of the inequality using the transposition method:
x – 12 > 100
x > 12 + 100 Transposition Method
x > 112
The solution set we have obtained is x > 112, or the set of all real numbers greater than 112. What do you think is the smallest whole number in the set x > 112? That number is 113.
Note that the answer is not 112 since 112 is excluded in x > 112.
Therefore, the answer is 113.
3. Using the Division Property of Inequality
The type of linear inequality in one variable we have solved so far is that with a numerical coefficient 1. But what if the numerical coefficient of the variable is not one, such as in 2x + 1 < 9?
We use the division property of inequality to solve this type of inequality.
Example 1: Let us try to solve 2x + 1 < 9.
Solution: Again, we want to isolate x from other quantities and make it the only quantity remaining on the left-hand side. To achieve that, we can transpose 1 to the right-hand side:
2x + 1 < 9
2x < -1 + 9 Transposition Method
2x < 8
Now, we still have 2x on the left-hand side. We want it to be x only. To eliminate the numerical coefficient 2, we have to divide both sides of the inequality by 2.
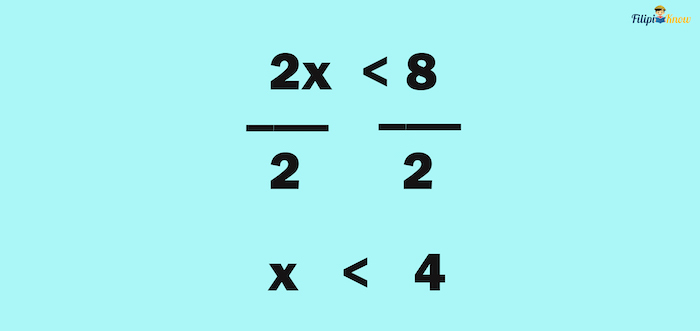
Thus, the solution set of the inequality is x < 4.
Example 2: Solve for the inequality 5x – 8 < 12
Solution:
5x – 8 < 12
5x < 8 + 12 Transposition Method
5x < 20
5x⁄5 < 20⁄5 Dividing both sides by 5 (DPI)
x < 4
Take note that there’s an important thing you have to consider when dividing both sides of an inequality. As per the division property of inequality, if you divide both sides of an inequality by a negative number, the inequality sign will be reversed.
Example 3: Let us try to solve -3x + 4 > 22
Solution: We start by transposing 4 to the right-hand side:
-3x > -4 + 22
-3x > 18
To make x the only quantity on the left-hand side, we have to divide both sides by -3. After we divide both sides of the inequality by -3, the inequality sign will be reversed per the division property of inequality:
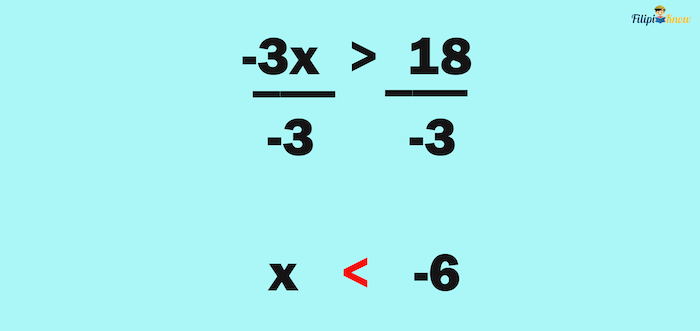
Thus, the answer is x < -6. This implies that any number less than -6 will satisfy the given inequality.
Example 4: Solve the inequality 16 – 8x ≤ 80
Solution: We start by transposing 16 to the right-hand side of the inequality:
16 – 8x ≤ 80
-8x ≤ -16 + 80
-8x ≤ 64
Our goal is to make x the only quantity on the left-hand side and get rid of -8. To do it, we have to divide both sides of the inequality by -8. However, note that we must reverse the inequality sign after the division process since we divide by a negative number.
-8x ≤ 64
(-8x)/-8 ≤ 64/-8 Dividing both sides by -8
x ≥ -8 Inequality sign is reversed
The solution set is x ≥ -8.
More Examples of Solving Linear Inequalities in One Variable
Example 1: Solve the inequality 15 < 3 + 2x
Solution: Our goal is to make x the only quantity on one side of the inequality. Since the variable x is already on the right-hand side, our next move is to transpose 3 to the left-hand side of the inequality:
15 < 3 + 2x
-3 + 15 < 2x
12 < 2x
Now, to make the x the only quantity on the right-hand side, we can divide both sides of the inequality by 2:
12 < 2x
12/2 < 2x/2
6 < x
Note that we can make 6 < x into x > 6 by the reversal property of inequality.
Thus, the answer to this example is x > 6.
Example 2: Solve the following inequality:
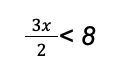
Solution: Notice that the left-hand side of the inequality is fractional; it has a denominator of 2. We can remove the denominator by multiplying both sides of the inequality by 2:
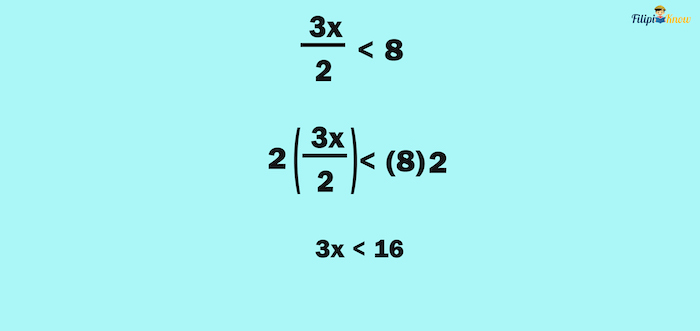
Now, we have 3x < 16. We can divide both sides of the inequality by 3:
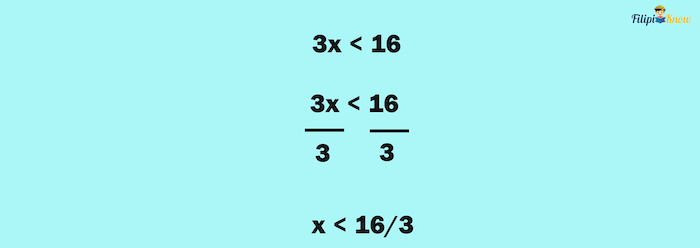
Thus, the solution set of this inequality is x < 16/3.
This means that any number less than 16/3 will satisfy the given inequality.
Example 3: What is the smallest whole number that will satisfy the inequality x + 4 < 2x – 7?
Solution: To solve this inequality, our goal is to isolate x from other quantities. We can start by transposing 2x to the left-hand side:
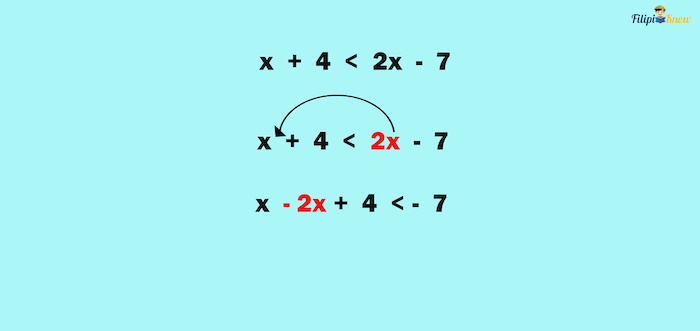
Now, we can also transpose 4 to the right-hand side so that the only terms that will remain on the left-hand side are those that have the x variable only:
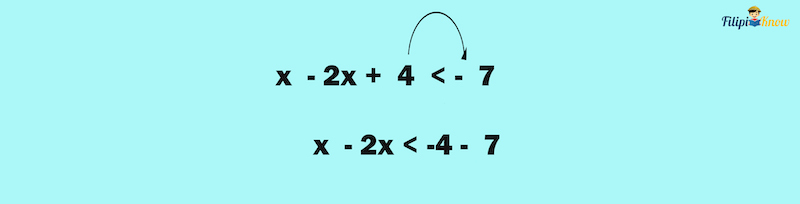
Simplifying and solving for inequality:

The solution set is x > 11. The smallest whole number in this set is 12.
Thus, our answer for this example is 12.
Solving Word Problems Involving Linear Inequalities
Now that you know the techniques for solving a linear inequality, let us try to solve word problems involving linear inequalities. Here are the steps:
- Determine what is being asked in the problem.
- Use a variable to represent the unknown in the problem.
- Create a linear inequality that describes the given problem.
- Solve the linear inequality and the given problem.
Example 1: The sum of a number and 32 is less than or equal to 8. Determine the possible values of the number.
Solution:
1. Determine what is being asked in the problem.
The problem asks us to find all the possible values of an unknown number such that the sum of that number and 32 is less than or equal to 8.
This means that the answer to this problem is not a single number but a set of numbers.
2. Use a variable to represent the unknown in the problem.
Let x represent the unknown number in the given problem.
3. Create a linear inequality that describes the given problem.
The problem states that the sum of the number and 32 is less than or equal to 8. Hence, we can write the inequality as follows:
x + 32 ≤ 8
4. Solve the linear inequality and the given problem.
Let us solve the inequality we have derived above.
x + 32 ≤ 8
x ≤ -32 + 8 Transposition Method
x ≤ -24
Thus, the solution set of the inequality is x ≤ -24. This means all numbers less than or equal to -24 will satisfy the inequality x + 32 ≤ 8.
Example 2: Jim has ₱200 for his science project. He expects to receive money from his mother to help him fund his project. Jim believes that he needs at least ₱1000 to finish the project. Given this situation, what is the smallest amount of money that Jim’s mother should give so Jim can finish the project?
Solution:
1. Determine what is being asked in the problem.
The problem is asking us to find the smallest amount of money Jim’s mother should give so that Jim can finish the project. Since we are looking for the smallest amount of money from the set of all possible amounts that can satisfy the given condition, our answer to the problem should be a single number only.
2. Use a variable to represent the unknown in the problem.
Let x represent the amount of money that Jim’s mother will give.
3. Create a linear inequality that describes the given problem.
The problem states that Jim already has ₱200 and expects to receive additional money from his mother (represented by x). Thus, the total amount of money that Jim will have is x + 200.
Jim needs at least (greater than or equal to) ₱1000 to complete the project. Thus, our inequality will be:
x + 200 ≥ 1000
4. Solve the linear inequality and the given problem.
Let us solve the inequality we have derived above.
x + 200 ≥ 1000
x ≥ -200 + 1000 Transposition Method
x ≥ 800
Thus, the solution set of the inequality is x ≥ 800. Jim’s mother should give any amount greater than or equal to ₱800 so Jim can finish the project.
However, we are looking for the smallest amount of money Jim must receive from his mother, not the solution set. The smallest number in x ≥ 800 is 800 (800 is included in the solution set because of the equal sign).
Thus, the smallest amount of money that Jim’s mother should give is ₱800.
Next topic: Functions
Previous topic: Radical Expressions
Return to the main article: The Ultimate Basic Math Reviewer
Download Printable Summary/Review Notes
Download Printable Flashcards
Test Yourself!
1. Practice Questions [Free PDF Download]
2. Answer Key [Free PDF Download]
3. Math Mock Exam + Answer Key
Written by Jewel Kyle Fabula
in Civil Service Exam, College Entrance Exam, LET, NAPOLCOM Exam, NMAT, PMA Entrance Exam, Reviewers, UPCAT
Jewel Kyle Fabula
Jewel Kyle Fabula graduated Cum Laude with a degree of Bachelor of Science in Economics from the University of the Philippines Diliman. He is also a nominee for the 2023 Gerardo Sicat Award for Best Undergraduate Thesis in Economics. He is currently a freelance content writer with writing experience related to technology, artificial intelligence, ergonomic products, and education. Kyle loves cats, mathematics, playing video games, and listening to music.
Copyright Notice
All materials contained on this site are protected by the Republic of the Philippines copyright law and may not be reproduced, distributed, transmitted, displayed, published, or broadcast without the prior written permission of filipiknow.net or in the case of third party materials, the owner of that content. You may not alter or remove any trademark, copyright, or other notice from copies of the content. Be warned that we have already reported and helped terminate several websites and YouTube channels for blatantly stealing our content. If you wish to use filipiknow.net content for commercial purposes, such as for content syndication, etc., please contact us at legal(at)filipiknow(dot)net
