The previous chapter refreshed our minds with logical propositions, including their conjunction, disjunction, negation, implication, and biconditional. You have also learned the converse, inverse, and contrapositive of conditional statements. Our discussion focused on these concepts, especially their truth values (i.e., whether they are true or false).

We identified the truth values of those statements just by analyzing them. However, it can become tedious to identify the truth values of statements, especially if they are too long or complex.

For this reason, we must have a reliable and convenient method to identify truth values.

This review introduces how to use truth tables – a powerful tool in propositional logic. Also, you will learn what logical equivalences are and how truth tables can be used to describe them.

Click below to go to the main reviewers:

Ultimate UPCAT Reviewer

Truth Value of a Proposition: A Review

We have discussed in the previous review that a proposition can only have one truth value. A proposition can be true (T) or false (F). The Law of Excluded Middle tells us that a proposition can’t be both true and false simultaneously.

A proposition is true if it states true or correct information and false if otherwise. 

Meanwhile, if we are dealing with complex propositions formed using connectives such as conjunctions (∧), disjunctions (∨), negation (⇒), conditional statement (or implication) (⇒), and biconditional statement (⇔), the truth value of the statement depends on the truth values of the respective propositions that composed it.  

To refresh our minds about how to identify the truth value of conjunctions, disjunctions, negations, conditional statements, and biconditionals, we summarize what we have learned from the previous reviewer in the table below:

Connective	Truth Value
Conjunction (p ∧ q)	True if both p and q are true
Disjunction (p ∨ q)	True if at least one of p and q is true
Negation (∿p)	False if p is true and true if p is false
Conditional Statement (p ⇒ q)	False if p is true and q is false. Otherwise, true
Biconditional Statement (p ⇔ q)	True if p and q have the same truth values

Now that we have warmed up our minds with what we have learned from the last reviewer let us proceed with our topic for this chapter.

Truth Tables

We have stated earlier that the truth value of complex propositions formed by connectives depends on the individual truth values of its components. We can easily show how the truthfulness or falsity of a statement depends on its components using truth tables.

Let us start with the simplest case: the negation of a statement. Below is an example of a truth value for p and its negation ∿p.

p	∿p
T	F
F	T

What’s good about the truth table above is that it is very intuitive. Clearly, the table states that if p is a true proposition, then ∿p is false and vice versa. 

Now, let us create a truth table for p ∧ q:

p	q	p ∧ q
T	T	T
T	F	F
F	T	F
F	F	F

Let us analyze the table above.

The first row of the table shows the propositions p, q, and the conjunction p ∧ q. We have already learned that a conjunction p ∧ q is true if both p and q are true; as seen in the table, only row 2, where both p and q are true, shows a “true” truth value for the conjunction. 

The remaining rows provide a “false” truth value since, in those rows (rows 3 to 5), p and q are not both true. 

Now that you understand truth tables and what they represent, we can discuss how to construct a truth table. 

How To Construct Truth Tables

To construct a truth table for logical connectives (conjunction, disjunction, negation, etc.), we can follow the steps indicated below:

1. Determine how many propositions are involved in the statement. Let n be that number of propositions in the statement.
2. Construct a table with 2ⁿ rows to put the possible truth values of the propositions. Of course, you also have to include one additional row on top of the 2ⁿ rows to put the names of the propositions.
3. Assign all possibilities of truth values of each proposition. We will show later in our example how to perform this.
4. Use your knowledge of the truth values of connectives to identify the truth value for the column dedicated to the connective.

Sample Problem 1: Create a truth table for P ∧ Q

Solution: 

Step 1: Determine how many propositions are involved in the statement.

We have two propositions, P and Q. Thus, we have n = 2.

Step 2: Construct a table with 2ⁿ rows to put the possible truth values of the propositions.

Since we have n = 2, we must prepare a table with 2ⁿ = 2⁽²⁾  = 2 x 2 = 4 rows. We also need to include one additional row to put the proposition labels on top of these four rows. Hence, we have a table with five rows.

P	Q	P ∧ Q

We need to provide three columns for the table for proposition P, proposition Q, and the conjunction of interest P ∧ Q.

Step 3: Assign all possibilities of truth values of each proposition.

P	Q	P ∧ Q

Put truth values in the columns dedicated to the propositions (P and Q). It’s totally up to you how to assign truth values to them. However, please start with the first column for P to make it easier and more organized. An easy way to fill this column is by putting two “true” (T) and two “false” (F) (since there are four rows, we divide it by two so that the T’s and F’s have equal numbers). 

P	Q	P ∧ Q
T
T
F
F

We will assign truth values for the second column so that no combination will be repeated. In our case above, alternatingly assigning T’s and F’s for proposition Q is best. 

P	Q	P ∧ Q
T	T
T	F
F	T
F	F

Step 4: Use your knowledge of the truth values of connectives to identify the truth value for the column dedicated to the connective.

P	Q	P ∧ Q
T	T
T	F
F	T
F	F

We know that conjunction will be true only if both propositions are true. Therefore, we only put T in the second row because P and Q are both true in this row. For the other rows, we just put F since not both P and Q are true on those rows. 

P	Q	P ∧ Q
T	T	T
T	F	F
F	T	F
F	F	F

That’s it; we have made a truth table for conjunction. 

You can use the steps discussed in this section to create the respective truth tables for disjunction, conditional, and biconditional statements. We will present their respective truth tables below since it will be too long if we will discuss them one by one.

Truth Table for Disjunction

P	Q	P ∨ Q
T	T	T
T	F	T
F	T	T
F	F	F

Truth Table for Conditional Statement (or Logical Implication/“If and Then” Statement) 

P	Q	P ⇒ Q
T	T	T
T	F	F
F	T	T
F	F	T

Truth Table for Biconditional Statement 

P	Q	P ⇔ Q
T	T	T
T	F	F
F	T	F
F	F	T

We will use our knowledge of truth tables to identify the truth values of various complex statements.

Sample Problem 2: Create a truth table for P ∨ Q ⇒ R

Solution: 

Step 1: Determine how many propositions are involved in the statement.

Three propositions are involved: P, Q, and R. So, we have n = 3.

Step 2: Construct a table with 2ⁿ rows to put the possible truth values of the propositions.

Since we have n = 3, we need to prepare a table with 2³ = 8 rows plus one additional row where we can put the propositions’ names.

P	Q	R	P ∨ Q	P ∨ Q ⇒ R

There are five columns this time because three individual propositions (P, Q, and R) and two connectives are involved (disjunction and implication). 

Step 3: Assign all possibilities of truth values of each proposition.

We will start by filling the first column intended for proposition P. Since we have eight rows below column P,  we must put four T’s and four Fs in this column.

P	Q	R	P ∨ Q	P ∨ Q ⇒ R
T
T
T
T
F
F
F
F

For the second column, we fill it by putting alternating T and F.

P	Q	R	P ∨ Q	P ∨ Q ⇒ R
T	T
T	F
T	T
T	F
F	T
F	F
F	T
F	F

You might notice repeated combinations (row 1 and row 3); don’t sweat it because we have not yet assigned truth values for R. 

How you will fill the third column is crucial since you must avoid repeating any combination. It’s up to you to fill this column, so long as no combination is repeated. 

Here’s a suggestion, you can fill the third column by alternating two T’s and two F’s. Doing this will fill column “R” without repeating any combination. 

P	Q	R	P ∨ Q	P ∨ Q ⇒ R
T	T	T
T	F	T
T	T	F
T	F	F
F	T	T
F	F	T
F	T	F
F	F	F

Are there any repeated combinations? None! We’re good to go to the next section.

Step 4: Use your knowledge of the truth values of connectives to identify the truth value for the column dedicated to the connective.

P	Q	R	P ∨ Q	P ∨ Q ⇒ R
T	T	T
T	F	T
T	T	F
T	F	F
F	T	T
F	F	T
F	T	F
F	F	F

We’re on the fourth and fifth columns, which involve connectives. 

Let us start with the fourth column, the disjunction of P and Q. Note that a disjunction will be true if at least one of the propositions is true. Hence, P ∨ Q is true if at least one of P and Q is true. Rows 2, 3, 4, 5, 6, and 8 show at least one true proposition between P and Q. The remaining rows show neither true proposition, so we put F to them. 

P	Q	R	P ∨ Q	P ∨ Q ⇒ R
T	T	T	T
T	F	T	T
T	T	F	T
T	F	F	T
F	T	T	T
F	F	T	F
F	T	F	T
F	F	F	F

We’re now on the last column that pertains to P ∨ Q ⇒ R. To identify the truth values for each row under this column, we have to refer to the 4th column as the hypothesis and the 3rd column as the conclusion. 

Note that we must put F on rows 4, 5, and 8 since they show a true hypothesis and a false conclusion. The remaining rows must be true. 

P	Q	R	P ∨ Q	P ∨ Q ⇒ R
T	T	T	T	T
T	F	T	T	T
T	T	F	T	F
T	F	F	T	F
F	T	T	T	T
F	F	T	F	T
F	T	F	T	F
F	F	F	F	T

We have now completed a truth table for P ∨ Q ⇒ R.

Using the truth table above, can you identify the truth value of P ∨ Q ⇒ R if P is true, Q is false, and R is false?

P is true, Q is false, and R is false on row 5. In row 5, we can see the truth value of P ∨ Q ⇒ R. Hence, the answer to this question is F. 

Sample Problem 3: Identify the truth value of P ⇒ Q ∧ ∿R if P is true, Q is false, and R is false.

Solution: We can use a truth table to answer this. However, we don’t have to create an entire truth table since the problem already specified the truth values of each proposition.

We have three propositions (P, Q, and R) and three connectives (implication, conjunction, and negation). So, we prepare a table with six columns and two rows (1 for labels and 1 for truth values. 

P	Q	R	∿R	Q ∧ ∿R	P ⇒ Q ∧ ∿R

The problem states that P is true, Q is false, and R is false. We put these truth values in the second row:

P	Q	R	∿R	Q ∧ ∿R	P ⇒ Q ∧ ∿R
T	F	F

We use our knowledge of connectives to fill the remaining columns. For the fourth column, we only need to identify the truth value of the negation of R. Since R is F, then ∿R must be T.

P	Q	R	∿R	Q ∧ ∿R	P ⇒ Q ∧ ∿R
T	F	F	T

Now, Q ∧ ∿R must be false since not both Q and ∿R are true (Q is false). Hence, we put F in the fifth column. 

P	Q	R	∿R	Q ∧ ∿R	P ⇒ Q ∧ ∿R
T	F	F	T	F

The last column, P ⇒ Q ∧ ∿R, means we have P as the hypothesis and Q ∧ ∿R as the conclusion. Based on the table above, P is true while Q ∧ ∿R is false. This means we have a true hypothesis and a false conclusion, implying that the conditional statement must be false. Hence, we put F in the last column. 

P	Q	R	∿R	Q ∧ ∿R	P ⇒ Q ∧ ∿R
T	F	F	T	F	F

Therefore, the truth value of P ⇒ Q ∧ ∿R if P is true, Q is false, and R is false, is false. 

Sample Problem 4: Is Q ∨ ∿P ⇔ ∿R ∧ Q true if P, Q, and R are all true?

Solution: The statement Q ∨ ∿P ⇔ ∿R ∧ Q is highly complicated. But, with the help of truth tables, we can quickly identify its truth value, given that P, Q, and R are all true. 

Again, we don’t have to create an entire truth table in this case since we are already interested in the truth value of the given statement if all P, Q, and R are true. 

Let’s start by constructing a table. We have three propositions (P, Q, and R) and five connectives (disjunction, biconditional, negation, and conjunction). Hence, we will have an 8-column table. We put T for P, Q, and R since this fact is given in the problem.

P	Q	R	∿P	Q ∨ ∿P	∿R	∿R ∧ Q	Q ∨ ∿P ⇔ ∿R ∧ Q
T	T	T

Since P is T, then ∿P is F. Also, since R is T, we can conclude that ∿R is F. 

P	Q	R	∿P	Q ∨ ∿P	∿R	∿R ∧ Q	Q ∨ ∿P ⇔ ∿R ∧ Q
T	T	T	F		F

Since Q is T and ∿P is F, then Q ∨ ∿P must be T since at least one of the propositions is true. 

P	Q	R	∿P	Q ∨ ∿P	∿R	∿R ∧ Q	Q ∨ ∿P ⇔ ∿R ∧ Q
T	T	T	F	T	F

Since ∿R is F and Q is T, then ∿R ∧ Q is F since not both of the propositions are true. 

P	Q	R	∿P	Q ∨ ∿P	∿R	∿R ∧ Q	Q ∨ ∿P ⇔ ∿R ∧ Q
T	T	T	F	T	F	F

Lastly, to identify whether Q ∨ ∿P ⇔ ∿R ∧ Q is true, we have to look at the truth values of Q ∨ ∿P   and ∿R ∧ Q . We can see from the table that Q ∨ ∿P is T while ∿R ∧ Q is F. 

Recall that in a biconditional statement, if the statements on the left and the right of the arrow are not of the same truth value, then the biconditional is F. Hence, Q ∨ ∿P ⇔ ∿R ∧ Q must be false. 

P	Q	R	∿P	Q ∨ ∿P	∿R	∿R ∧ Q	Q ∨ ∿P ⇔ ∿R ∧ Q
T	T	T	F	T	F	F	F

Therefore, if P, Q, and R are all true, then Q ∨ ∿P ⇔ ∿R ∧ Q is false. 

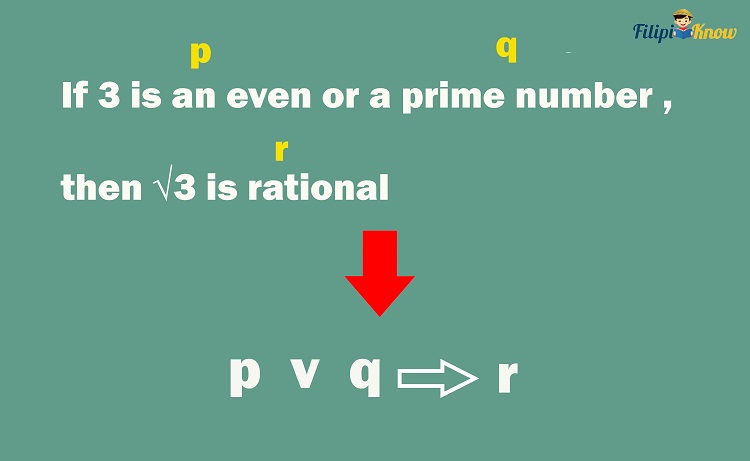
Sample Problem 5: Identify the truth value of “If 3 is an even or a prime number, then √3 is rational.”

Solution: Let us start by assigning propositional variables to each proposition in the given statement.

• Let p be the proposition “3 is an even number.” This is a false proposition since 3 is an odd number. 
• Let q be the proposition “3 is a prime number.” This is a true proposition. The only factors of 3 are 3 and itself.
• Let r be the proposition “√3 is rational.” This is false, as this radical is an irrational number.

By translating the statement “If 3 is an even or a prime number, then √3 is rational” into a statement with propositional variables p, q, and r, we will obtain p∨ q ⇒ r.

Let us create a truth table to identify whether p ∨ q ⇒ r is true or false. Recall that we have stated earlier that p is false, q is true, and r is false.

p	q	r	p ∨ q	p ∨ q ⇒ r
F	T	F

The conjunction p ∨ q must be T since one of p and q is true. 

p	q	r	p ∨ q	p ∨ q ⇒ r
F	T	F	T

The hypothesis in p ∨ q ⇒ r is p ∨ q, which is T based on the truth table above. Meanwhile, the conclusion, which is r, is false. So, we have a true hypothesis and a false conclusion in p ∨ q ⇒ r. Hence, p ∨ q ⇒ r is false.

p	q	r	p ∨ q	p ∨ q ⇒ r
F	T	F	T	F

The answer is false.

Tautology, Contradiction, and Contingency

A tautology is a statement that is always true regardless of the truth value of the propositions. 

For instance, the statement p ∨ ∿p is a tautology since it is always true regardless of the truth value assigned to p and p. 

Shown below is the truth value of p ∨ ∿p.

p	∿p	p ∨ ∿p
T	T	T
F	T	T

Notice that whatever the truth values of p and ∿p, p ∨ ∿p is a true statement. Hence, p ∨ ∿p is an example of a tautology.

What is a real example of p ∨ ∿p, which is a tautology? 

Consider p as the proposition “3 is an odd number.” Then, ∿p is “3 is an even number.” Hence p ∨ ∿p is “3 is an odd or even number.” The statement “3 is an odd or even number” is a tautology since this statement is always true. 

The opposite of tautology is a contradiction.  A contradiction is a statement that is always false regardless of the truth value of the propositions. 

For instance, the statement p ∧ ∿p is an example of contradiction. This means that whatever the truth value of p and ∿p, the truth value of p ∧ ∿p is always false.

See how p ∧ ∿p is always false in the truth table below. 

p	∿p	p ∧ ∿p
T	F	F
F	T	F

If a proposition is neither a tautology nor a contradiction, the proposition is called a contingency. In this case, its truth value varies depending on the truth values of the propositions.

For example, p ⇒ ∿p is a contingency since its truth value varies. Refer to its truth table below and observe its truth values.

p	∿p	p ⇒ ∿p
T	F	F
F	T	T

Note that the truth value of p ⇒ ∿p is not always true or not always false. Hence, p ⇒ ∿p is a contingency.

Sample Problem: Determine if the following is a tautology, contradiction, or contingency.

1. (P ∧ Q) ⇒ P
2. P ∨ ∿Q ⇔ Q

Solution: 

1. For (P ∧ Q) ⇒ P:

P	Q	P ∧ Q	(P ∧ Q) ⇒ P
T	T	T	T
T	F	F	T
F	T	F	T
F	F	F	T

Based on the truth table above, the truth values of (P ∧ Q) ⇒ P are always true regardless of the truth values of P and Q. Hence, (P ∧ Q) ⇒ P is a tautology.

2. For P ∨ ∿Q ⇔ Q:

P	Q	∿Q	P ∨ ∿Q	P ∨ ∿Q ⇔ Q
T	T	F	T	T
T	F	T	T	F
F	T	F	F	F
F	F	T	T	F

Based on our truth table above, the truth values of P ∨ ∿Q ⇔ Q vary (it is not always true or false). Hence, P ∨ ∿Q ⇔ Q is considered a contingency.

Logical Equivalence

Two statements are logically equivalent if they always have the same truth value. In other words, logical equivalent statements will produce similar truth values regardless of the truth values of the propositions.

Formally:  Two statements m and n are logically equivalent (In symbols, m ≡ n) if m ⇒ n is a tautology.

To make the concept of logical equivalence much clearer, consider these statements:

• Statement 1 : P ⇒ Q
• Statement 2: ∿Q ⇒ ∿P

Let us create the respective truth tables of each statement.

Statement 1 truth table:

P	Q	P ⇒ Q
T	T	T
T	F	F
F	T	T
F	F	T

Take note of the truth values of P ⇒ Q.

Statement 2 truth table: 

P	Q	∿P	∿Q	∿Q ⇒ ∿P
T	T	F	F	T
T	F	F	T	F
F	T	T	F	T
F	F	T	T	T

Now, compare the truth values of P ⇒ Q and ∿ Q ⇒ ∿ P. 

Truth values of P ⇒ Q	Truth values of ∿Q ⇒ ∿P
T	T
F	F
T	T
T	T

Note how the truth values of the statements are the same for every assigned combination of truth values of P and Q.

This means that  P ⇒ Q and ∿Q ⇒ ∿P are logically equivalent. 

What have you noticed about  P ⇒ Q and ∿ Q ⇒ ∿ P? Yes, they are contrapositives! 

Here’s an interesting fact: The contrapositive of a conditional statement and the conditional statement itself are logically equivalent. This also means a conditional statement is true if its contrapositive is true. This property is known as the Law of Contraposition. 

Sample Problem 1: Alice said, “If I live in Manila, then I live in the Philippines.” Celine heard this and tried to restate it as “If Alice doesn’t live in the Philippines, then she does not live in Manila.” Are Alice and Celine’s statements logically equivalent?

Solution: Yes, since Celine’s statement is just the contrapositive of Alice’s statement.

Note that a conditional statement and its contrapositive are logically equivalent. 

Sample Problem 2: Are P ⇒ Q and ∿P ∨ Q logically equivalent?

Solution: We use truth tables to show whether P ⇒ Q and ∿ P ∨ Q are logically equivalent:

The truth table for P ⇒ Q:

P	Q	P ⇒ Q
T	T	T
T	F	F
F	T	T
F	F	T

The truth table for ∿ P ∨ Q:

P	Q	∿P	∿ P ∨ Q
T	T	F	T
T	F	F	F
F	T	T	T
F	F	T	T

Comparing the truth tables above, we can see that P ⇒ Q and ∿P ∨ Q have the same truth values for every assigned combination of truth values of P and Q. For this reason, we conclude that P ⇒ Q and ∿P ∨ Q are logically equivalent. In symbols: P ⇒ Q ≡ ∿P ∨ Q.

We have shown that P ⇒ Q and ∿P ∨ Q are logically equivalent. Let us provide a concrete example of a statement that represents them. 

Let P be “Fred knows algebra,” and Q be the proposition “Fred is a high school student.” Then, P ⇒ Q is translated as “If Fred knows algebra, then he is a high school student,” and ∿P ∨ Q is translated as “Fred does not know algebra, or he is a high school student.” 

Since we have shown that P ⇒ Q ≡ ∿P ∨ Q, the statements “If Fred knows algebra, then he is a high school student” and “Fred does not know algebra, or he is a high school student” are logically equivalent. This means that if the statement “If Fred knows algebra, then he is a high school student” is true, “Fred does not know algebra, or he is a high school student” is also true.

Properties of Logical Equivalence

Commutative Law	p ∨ q ≡ q ∧ p p ∧ q ≡  q ∨ p
Associative Law	(p ∨ q) ∨ r ≡ p ∨ (q ∨ r) (p ∧ q)  ∧ r  ≡  p  ∧ (q  ∧ r)
Distributive Law	p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r) p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
De Morgan’s Law	∼(p ∨ q) ≡ ∼p ∧ ∼q ∼(p ∧ q) ≡ ∼p ∨ ∼q
Equivalence of an Implication and a Contrapositive	p ⇒ q ≡ ∼q ⇒ ∼p
Negation of an Implication	∼(p ⇒ q) ≡ p ∧ ∼q
Idempotent Laws	p ∨ p ≡ p p ∧ p ≡  p
Implication to Disjunction Law	p ⇒ q ≡ ∼p ∧ q

This section will discuss the essential properties of logical equivalence that can help us identify whether two given statements are logically equivalent without using truth tables. 

1. Commutative Law

The commutative law states that the order of propositions in conjunction and a disjunction is unimportant, but the disjunction sign flips to the conjunction sign (and vice versa).

For instance, “Jessie is a French and a college student” is logically equivalent to “Jessie is a college student and a French.”

Hence, if “Jessie is a French and a college student” is true, then “Jessie is a college student and a French” will also be true. Similarly, if “Jessie is a French and a college student” is a false statement, then “Jessie is a college student, and a French” is also false.

2. Associative Law

This property tells us that in conjunction and disjunction, the groupings of the propositions do not matter and will always yield the same truth values. This means that (p v q) v r will have identical truth values with p v (q v r) (You can try proving this using truth tables).

3. Distributive Law

The distributive law of logical equivalence allows us to distribute an outer connective to an inner connective. 

For instance, in p ∨ (q ∨ r), we distribute “p ∨” to (q ∨ r) to obtain (p ∨ q) ∧ (p ∨ r). Note that in between (p ∨ q) and (p ∨ r), we have to put the opposite of “∨” (disjunction symbol), which is the “∧” (conjunction symbol). 

Similarly, we can distribute “p ∧” to (q ∧ r) to obtain (p ∧ q) ∨ (p ∧ r). We have to put the opposite of “∧” (conjunction symbol), which is “∨” (disjunction symbol), in between the groups.

4. De Morgan’s Law

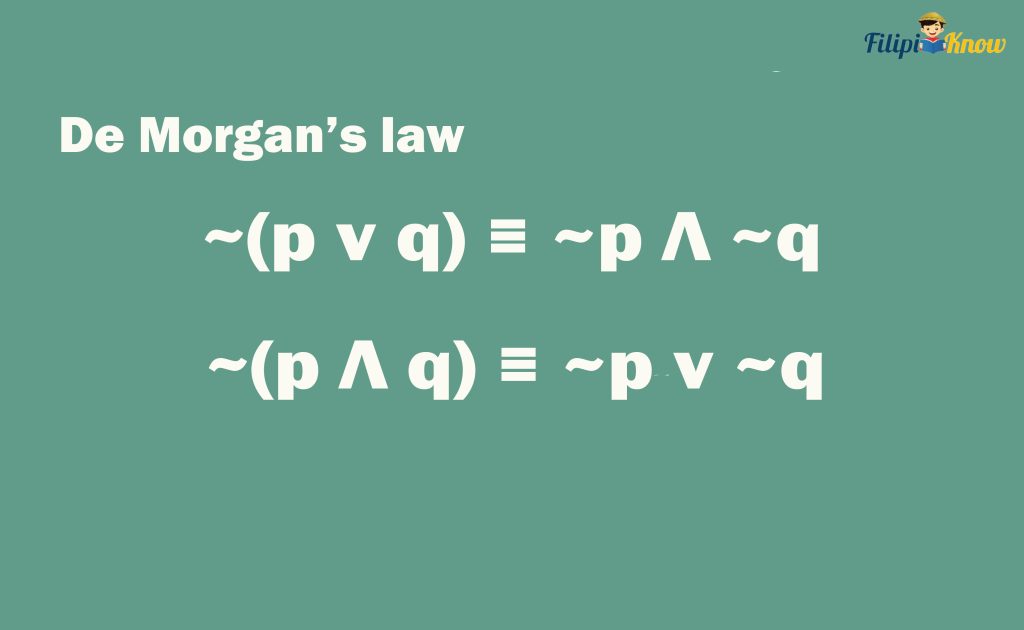
This law states that the negation of the disjunction of two statements is logically equivalent to the conjunction of the negation of each statement. Moreover, it also states that the negation of the conjunction of two statements is logically equivalent to the disjunction of the negation of each statement.

Consider the statement, “The building will be demolished or sold.” This statement is a disjunction of the statements: (1) “The building will be demolished” and (2) “The building will be sold.” According to De Morgan’s Law, if we negate a disjunction of two statements, the result will be the conjunction of the negation of the statements.

The negation of the first statement is, “The building will not be demolished.”

The negation of the second statement is, “The building will not be sold.”

The conjunction of these statements is “The building will not be demolished and will not be sold.”

Therefore, the negation of the statement “The building will be demolished or sold” is  “The building will not be demolished and will not be sold.” 

Sample Problem 1: Consider the statement “x is a whole number and an integer.” Note that this statement is a conjunction of two statements: (1) x is a whole number, and (2) x is an integer. According to De Morgan’s law, if we negate the conjunction of two statements, we should obtain the disjunction of the negation of the statements.

The negation of the first statement is: “x is not a whole number.”

The negation of the second statement is “x is not an integer.”

The disjunction of these statements is “ x is neither a whole number nor an integer.”

Therefore, by De Morgan’s law, the negation of the statement “x is a whole number and an integer.” is “ x is neither a whole number nor an integer.”

Sample Problem 2: Use De Morgan’s law to construct the opposite or negation of the statement, “It is prohibited to bring pets or sharp objects into the hotel.” 

The given statement is a disjunction of two statements: (1) It is prohibited to bring pets into the hotel, and (2) It is prohibited to bring sharp objects into the hotel. According to De Morgan’s Law, the negation of the disjunction of two statements can be obtained by taking the conjunction of the negation of the statements.

The negation of the statement: It is prohibited to bring pets into the hotel is It is allowed to bring pets into the hotel.

The negation of the statement: It is prohibited to bring sharp objects into the hotel is It is allowed to bring sharp objects into the hotel.

The conjunction of these statements is: It is allowed to bring pets and sharp objects into the hotel.

Thus, per De Morgan’s Law, the negation of the given statement is, “It is allowed to bring pets and sharp objects into the hotel.” 

5. Equivalence of an Implication and a Contrapositive Law

Also known as the law of contraposition, this rule states that given a conditional statement or a logical implication, its contrapositive is logically equivalent to itself.

For instance, “If p is an integer, then it is a rational number” is logically equivalent to its contrapositive “If p is not a rational number, then p is not an integer.” This implies that if the first statement is true, the second (the contrapositive) is also true (the same case if false).

6. Negation of an Implication

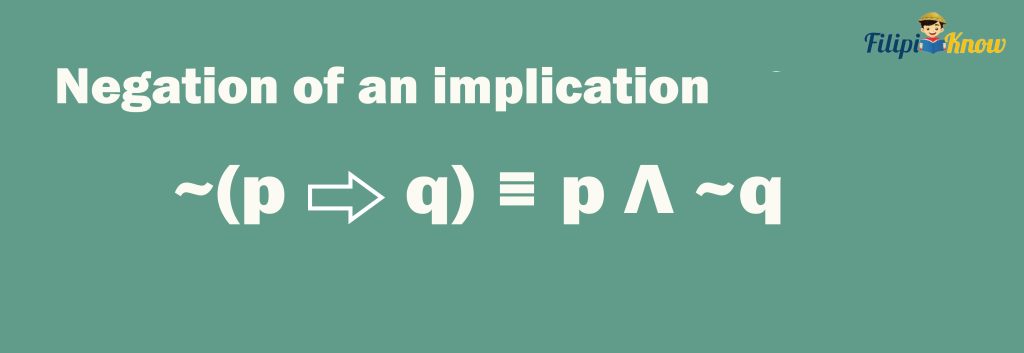
According to this law, the negation of a logical implication (or a conditional statement) is logically equivalent to the conjunction of its hypothesis and the negation of its conclusion.

Suppose we want to negate the conditional statement, “If I write a poem, then I’m inspired.” We can form it by simply constructing the conjunction of the hypothesis “I write a poem” and the negation of the conclusion “I’m not inspired.” Hence, the negation of the given conditional statement is, “I write a poem, but I’m not inspired.”

7. Idempotent Laws

This law states that the conjunction of a statement to itself is logically equivalent to the statement itself. Similarly, the disjunction of a statement to itself is logically equivalent to the statement itself.

8. Implication to Disjunction

This law states that a conditional statement or logical implication is logically equivalent to the disjunction of the negation of the hypothesis and the conclusion.

Consider the statement, “If you obtained a 95% in the exam, you would be the class valedictorian.” We can rewrite this conditional statement into an equivalent disjunction of the negation of the hypothesis “You obtain a 95% in the exam” and the conclusion “You will be the class valedictorian.” 

You might be wondering how this disjunction “You will not obtain a 95% in the exam, or you will be the class valedictorian” becomes logically equivalent to “If you obtained a 95% in the exam, you would be the class valedictorian.” 

Hence, the conditional statement can be rewritten as a disjunction: “You will not obtain a 95% in the exam, or you will be the class valedictorian.” 

Analyze the disjunction again. It tells you two things that are exclusive from each other. In other words, only one can happen between “not obtaining a 95%” and “being a class valedictorian.” These two cannot occur at the same time.

So, if you failed to obtain a 95%, being a class valedictorian is already impossible. This is precisely in line with what the original statement states, which implies that getting a 95% is the condition to be the class valedictorian.

Previous topic: Propositional Logic

Return to the main article: The Ultimate Basic Math Reviewer

Download Printable Summary/Review Notes

Download Printable Flashcards

Test Yourself!

1. Practice Questions [Free PDF Download]

2. Answer Key [Free PDF Download]

3. Math Mock Exam + Answer Key