Work, Energy, and Power

We all experience work, energy, and power daily. But how well do you know them if viewed through the lens of physics? This reviewer lets you rediscover the joy of studying these principles and their impact on our everyday lives.
Click below to go to the main reviewers:
Table of Contents
Work

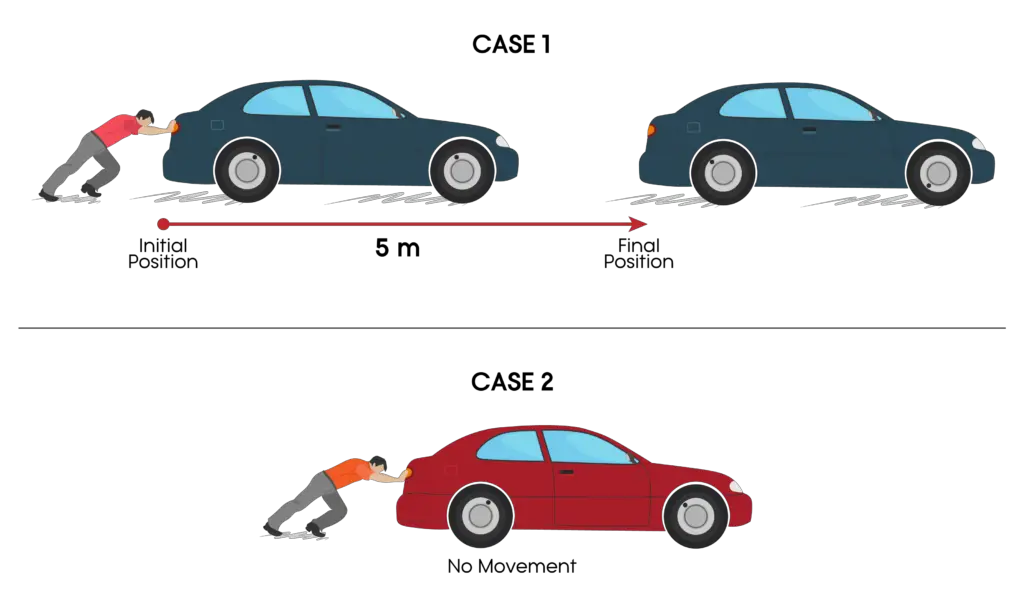
You probably know how hard it is to push a car that has been stranded in the middle of the road. You know you are making your car move by applying force to it, resulting in work done on the car.
But what is work?
Many people define work differently, but in physics, work is defined as an action done on an object wherein an applied force causes a displacement of the object.
In our example, the car moves from one place to another (even just a little). Your work is greater if the force you apply is greater and the displacement is greater.
Mathematically,
W = F ⋅ d
Work can only be done when displacement occurs.
Suppose you are pushing that car with a constant force of 235 N over the 5-meter distance; you would do 1175 Newton meters of work. Newton-meters is also known as Joules, named after the physicist James Prescott Joule.
When you push the same car and apply the same force, but the car did not move, you may get tired, but there is no work done.
Moreover, only the force components parallel to the displacement count toward work.
If you push the car with your arms parallel to the ground, all the force contributes to the work. However, if you are pushing at a downward angle, only the x-component contributes to work, but the y-component does not. In this situation, we are going to use the equation
W = Fd cos θ
where F is the magnitude of the force, d is the magnitude of the displacement, and θ is the angle from the horizontal.
Note that when there is no angle (θ = 0), work is just equal to Fd, while when you push the box downward (θ = 90), there will be no work done since cos 90 is equal to 0.
Note that work is a scalar quantity, meaning it can be positive or negative. Work is positive if the force is applied in the same direction as the displacement, while work is negative if the applied force is in the opposite direction of the displacement.
Always be mindful of the signs since it tells us about the speed resulting from the work applied.
Suppose you have a block that slides on a frictionless surface. Three forces are acting on the block: the weight w, the normal force n, and the force F exerted on the block by the hand.
If you push to the right on the block as it moves, the net force on the block is in the direction of the motion, which means that the total work done on the block is positive. This means that the block speeds up. However, if you push to the left on the block as it moves, the net force on the block will be in the opposite direction of the motion, making the total work done on the block negative.
The block then slows down. If you push straight down on the block as it moves, the net force on the block is zero, which means there is no work done on the block, and its speed remains the same.
Since work is a scalar quantity, the total work (Wtot) done on the object by all the forces is the algebraic sum of the quantities of work done by the individual forces.
Sample Problem
Find the work done by gravity to the boy whose mass is 40 kg and is climbing through a 1.35-meter ladder that makes a 60°angle with the tree.
Solution
We know that W = Fd cosθ. The force of gravity, also known as weight, is equal to
w = mass x acceleration due to gravity
w = (40 kg) (-9.8 m/s2)
w = -392 N
The displacement is upward along a 1.35-meter ladder.
Calculating for work,
W = Fd cosθ
W = (-392 N) (1.35 m) cos (60)
W = -264.6 J
Energy

Energy is defined as the ability to do work.
There are different types of energy, but we will concentrate on kinetic and potential energy.
1. Kinetic Energy
Kinetic energy is usually known as energy in motion.
We can also relate work with energy. Recalling Newton’s second law of motion, we know that when the net force is applied to an object, it will cause it to move at some constant acceleration.
F = ma [Eq. 1]
We also know that work is equal to the product of force and displacement.
W = Fd [Eq. 2]
If we substitute the value of F in Eq. 2, we will get
W = mad [Eq. 3]
Recalling one of the kinematic equations, we know that
ad = ½(vx2 – v0x2) [Eq. 4]
Substituting the value of the ad to Eq. 3, we will get
W = ½m (vx2 – v0x2)
This equation means that the product of force and displacement is the work done by the net force F and thus is equal to the total work (Wtot) done by all the forces acting on the particle.
The quantity ½mv2 is also called the kinetic energy of the particle. Thus, this equation can also be written as
W = ΔKE
otherwise known as the work-energy theorem.
This means that when work is done on the object, there will be a change in kinetic energy, which is also the energy in motion. This theorem also means that an object in motion can work on another object.
When an external force does work on a system, the amount of work will be equal to the change in the kinetic energy of the system. Take note that:
- W = positive (+) The system increases its kinetic energy, and the change will equal the work done ON the system.
- W = negative (-) The system decreases its kinetic energy, and the change will be equal to work done BY the system.
Mass is also related to kinetic energy. This means that the more massive an object is, the higher its kinetic energy.
Sample Problem
Use the work-energy theorem to find the force acting on a 7.6×106-kg meteorite that travels along a straight line from rest and covers 9.1×1015 meters with a speed of 155 m/s.
Solution
We know that the total work done is equal to the change in kinetic energy or simply
W = ΔKE
We also know that the total work done by a force F is equal to Fd cos θ.
So,
W = ½m (vx2 – v0x2)
W = Fd cos θ
Fd cos θ = ½m (vx2 – v0x2)
F = [½m (vx2 – v0x2)] / d cos θ
In this case, the meteorite travels along a straight line, so cos 0 = 1. It also started from rest, making our initial velocity equal to 0.
Our final equation will then be
F = [½m (vx2)] / d
Substituting the given values, we will have
F = [½ (7.6×106 kg) (155 m/s)2] / 9.1×1015 m
F = 1.003×10-5 N
2. Potential Energy
Potential energy (U) is the stored energy an object possesses due to its position relative to other objects.
A perfect example of this is lifting a ball in the air. When a ball is lifted in the air, its gravitational potential energy is increased as it moves farther away from the ground.
Note that the closer the object is to the earth’s center of gravity, the lesser the potential energy it possesses. As you lift an object up or away from the ground, the higher the potential energy it gains.
The potential energy due to an elevated position is known as the gravitational potential energy. This is equal to the work done against gravity in lifting it.
Work done equals the upward force an object needs to move at a constant velocity (weight) through a height h.
Mathematically,
Ugrav = mgh
Potential energy is usually meaningful when it changes. When work is done or converted from one form to another, just like when a ball is released from a high place, the potential energy will then be converted to kinetic energy as it falls. This perfectly describes the concept of conservation of energy.
Conservation of Energy
The law of conservation of energy states that energy cannot be created nor destroyed, but it can be transformed from one form to another without changing the total amount of energy.
Simply put, energy is always conserved.
In our example in the previous section, we say that when a ball falls, the potential energy will be converted to kinetic energy.
We should also take note that the sum of the energies will always be the same.
The sum of potential and kinetic energy is called mechanical energy. This type of energy only includes potential and kinetic energy. The remaining types of energy, such as chemical, thermal, nuclear, and others, are known as nonmechanical energy.
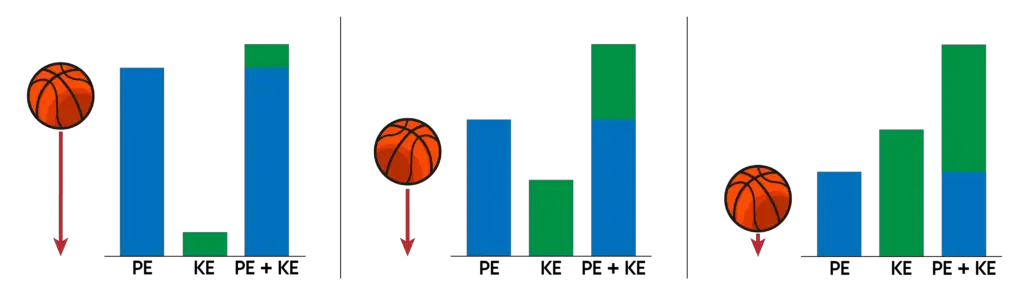
Let us have another example using a pendulum.
At the top of the swing, the pendulum possesses its maximum potential energy and zero kinetic energy. As it is released, its potential energy decreases while its kinetic energy increases until the ball reaches the bottom of the swing. At this position, the potential energy is at its minimum while the kinetic energy is at its maximum.

As the pendulum moves, its energy interchanges again and again, but the mechanical energy will always remain the same, hence, energy is conserved.
We can express this mathematically using the equation
ME = KE + PE
ME = ½mv2 + mgh
Since mechanical energy is conserved,
½mv0x2 + mgh1 = ½mvx2 + mgh2
Note that this equation only works when friction is neglected.
Power

The definition of work does not incorporate the concept of time, but if we want to know how much time it needs to get the work done, we need to understand power.
Power is the time rate of doing work.
Mathematically,
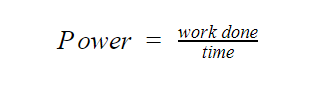
The SI unit for power is Watt, in honor of James Watt.
1 watt = 1 joule/second.
Common units for power include kilowatt, megawatt, and horsepower.
Note that although equal work is done in two objects, the power is different since it includes time.
Sample Problem
A 40-kg balikbayan box slides on the rough surface of the warehouse at 3 m/s and then stops due to friction. As the box stops, find the average power produced by friction if the coefficient of kinetic friction between the box and the surface is 0.245.
Solution
We are given the following quantities:
- mass = 40 kg
- v0x = 3 m/s
- vx = 0
- μk = 0.245
We know that P = W/t.
Calculating for work, we will get
W = ½m (vx2 – v0x2)
W = ½ (40 kg) (3 m/s)2
W = 180 J
To calculate time, we must relate Newton’s second law of motion and the concept of frictional force. We know that the acceleration of the box is given by
Fnet = -f
ma = -μkN
ma = -μkmg
a = -μkg
We also know that a = (vx – v0x)/t. Since vx = 0, a = – v0x/t.
– v0x/t = -μkg
t = v0x/μkg
Solving for t, we will get
t = 3 m/s / (0.235) (9.8 m/s2)
t = 1.3 s
Calculating for power,
P = W/t
P = 180 J/1.3 s
P = 138.5 W
Next topic: Momentum and Impulse
Previous topic: Friction
Return to the main article: The Ultimate Physics Reviewer
Download Article in PDF Format
Test Yourself!
1. Practice Questions [PDF Download]
2. Answer Key [PDF Download]
Written by Mary Joy Montenegro
Mary Joy Montenegro
Mary Joy Montenegro is a licensed professional teacher who obtained her Master’s Degree in Teaching Physics at De La Salle University under the Department of Science and Technology Scholarship. Aside from teaching, she also loves traveling and meeting other people.
Copyright Notice
All materials contained on this site are protected by the Republic of the Philippines copyright law and may not be reproduced, distributed, transmitted, displayed, published, or broadcast without the prior written permission of filipiknow.net or in the case of third party materials, the owner of that content. You may not alter or remove any trademark, copyright, or other notice from copies of the content. Be warned that we have already reported and helped terminate several websites and YouTube channels for blatantly stealing our content. If you wish to use filipiknow.net content for commercial purposes, such as for content syndication, etc., please contact us at legal(at)filipiknow(dot)net
