Solving Problems Involving Conversion of Units of Measurement

Measuring is one of the human activities that we perform daily. A tailor measures the length of the dress; a butcher measures the weight of the meat; a surveyor measures the area of large land masses, and so on.
The ability to measure objects is always connected to the history of our civilization. During ancient times, our ancestors used their fingers, hands, and feet to determine the length of an object. In this era, humans had varying ways of measuring things.
Eventually, after the French Revolution in the late 18th century, a standardized way of measurement was developed (i.e., the metric system). Today, we have a convention of measurement units and advanced technological tools to measure objects.
In this module, you’ll learn what measurement is, the units of measurement (for length, weight, volume, time, and temperature), and how to convert units in the metric system.
Click below to go to the main reviewers:
Ultimate PNP Entrance Exam Reviewer
Ultimate PMA Entrance Exam Reviewer
Table of Contents
What is Measurement?
Measurement is the provision of a numerical value to present and describe the magnitude or amount of a particular object.
We use measurement units to provide a more accurate description of the object’s measurement. Some examples of measurement units are meters, liters, grams, inches, Fahrenheit, and so on.
For instance, if we want to determine how long a piece of wood is, we measure its length. To do this, we use a particular SI unit of measurement (e.g., meters) and provide a number that describes the length of this wood (e.g., this wood is 3 meters long).
Since there are a lot of measurement units being used around the world, a standardized set of measurement units have been adopted by several countries. This is called the SI Units of Measurement, more commonly known as the Metric System (e.g., meter, gram, liter). On the other hand, there’s also the Imperial System or US Standard Units, which is also commonly used in the Philippines (e.g., feet, yards, pounds, etc.).
What Are the Different Ways To Measure Objects?
There are different ways to measure objects depending on the particular trait we want to describe or show.
1. Length

This refers to the distance from one point to another. In other words, this describes how long or short an object is. Standard measurement units are meters, centimeters, inches, feet, etc.
The SI base unit for length is a meter.
2. Area

This refers to the amount of space occupied by a two-dimensional figure. In other words, it tells us how much surface a plane figure covers. Commonly used measurement units are square meters, square kilometers, square yards, etc.
Metric units of the area have an exponent of 2 to indicate that we are measuring the amount of two-dimensional space occupied (e.g., the square meter is written as m2).
The SI base unit for the area is square meters (m2).
3. Volume or Capacity

The volume is the space occupied or enclosed by a three-dimensional figure. Commonly used measurement units are cubic meters, cubic kilometers, cubic yards, etc.
Metric volume units have an exponent of 3 to indicate that we are measuring the amount of three-dimensional space occupied (e.g., a cubic meter is written as m3).
4. Mass

In Physics, mass and weight mean differently. Mass refers to the amount of matter an object has, while weight refers to the force that gravity exerts on an object.
The SI base units for mass and weight are different. The kilogram is the SI base unit for mass, while Newton is the SI base unit for weight.
However, outside a Physics classroom, these terms are often used interchangeably. Many people perceive mass and weight as the same thing, which refers to how heavy an object is. To avoid ambiguity and confusion in our discussion, we will strictly use in this article the word “mass” to refer to the heaviness of an object
5. Time
This refers to the duration of the sequence of events. For instance, we measure time to determine how long you read this reviewer.
The SI base unit for time is seconds.
6. Temperature

Temperature tells us how hot or cold an object is. In Physics, the temperature is the average kinetic energy of the particles of an object. The primary way to measure temperature is through a thermometer.
SI base unit for temperature is Kelvin (K). However, Celsius (°C) and Fahrenheit (°F) are the more popular units.
This review will discuss the conversion of measurement units for length, area, volume, mass, time, and temperature. However, remember that these are not just the ways to measure objects. For instance, we can also measure their luminous intensity, electric current, amount of substance, and so on.
Metric System Units of Length
We learned earlier that meter (m) is the SI base unit for length. This means that other metric units for length are derived from the meter. For instance, a kilometer (km) means 1000 meters.
In the metric system, we use prefixes to indicate that a particular metric unit is a multiple of the base unit. For example, the prefix “kilo” means 1000 times the base unit. So, 1 km = 1000 meters.
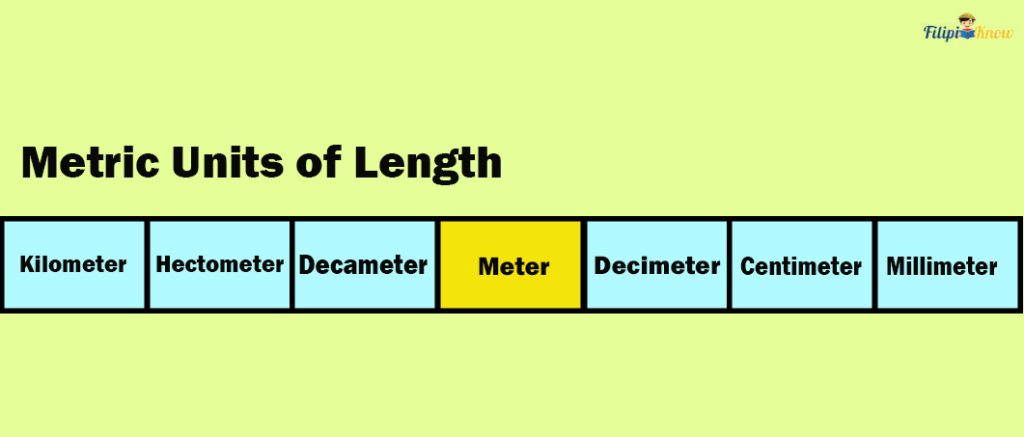
Six prefixes are used in the metric system, and we list them below together with their equivalent value in the base unit.
| 1 kilometer (km) | 1000 meters |
| 1 hectometer (hm) | 100 meters |
| 1 decameter (dam) | 10 meters |
| 1 meter (m) | 1 meter |
| 1 decimeter (dm) | 0.1 meter |
| 1 centimeter (cm) | 0.01 meter |
| 1 millimeter (mm) | 0.001 meter |
An easier way to visualize these prefixes is by using a table:
Whether you want to memorize the conversion table above is up to you. However, it is advisable to remember the equivalent value of each prefix in terms of the base unit. These prefixes also apply to metric units for area and mass.
Converting Metric Units of Length
The easiest way to convert metric units is by simply moving decimal places.
For instance, let us convert 375 meters to kilometers by looking at the table of prefixes below.
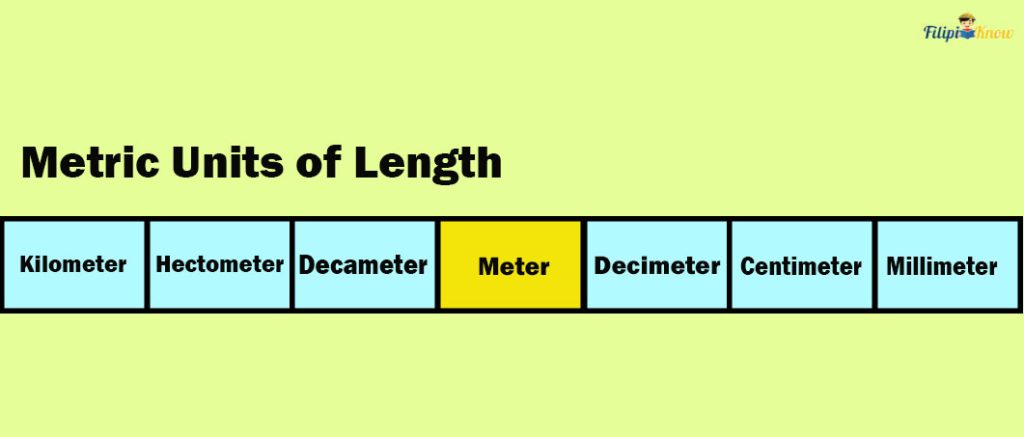
Note that the table above has three steps to the left from meter to kilometer. This means we must move three decimal places to the left in 375 meters to get its equivalent in kilometers.

This means that 375 meters are equal to 0.375 kilometers.
Sample Problem 1: Convert 98.35 decameters to centimeters
Solution: Looking at the table of metric units of length, there are three steps to the right, from decameters to centimeters.
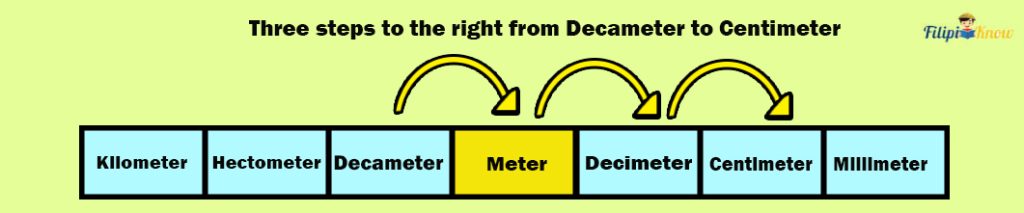
This implies that we must move three decimal places to the right to convert 98.35 decameters to centimeters.

Hence, 98.35 decameters = 98,350 centimeters
Sample Problem 2: A ribbon was divided into two strips. The first strip measures 176.50 centimeters, while the second measures 89.56 centimeters. What is the length of the original ribbon in meters?
Solution: There are two steps to the left from centimeters to meters. Hence, we move two decimal places to the left to convert centimeters to meters.
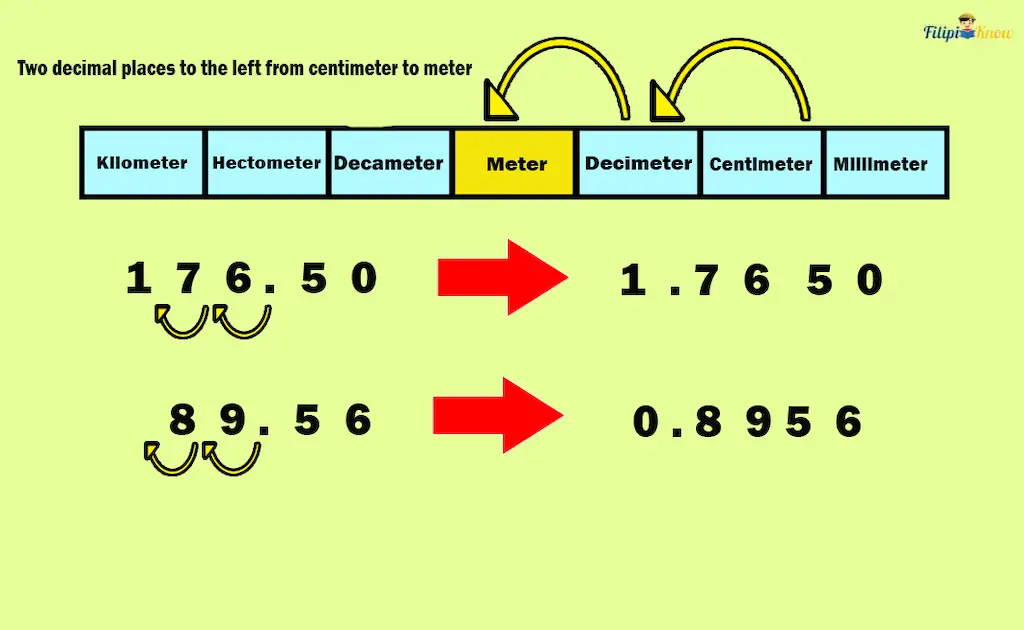
- Moving two decimal places in 176.50 centimeters results in 1.7650 meters.
- Moving two decimal places in 89.56 centimeters results in 0.8956 meters.
Adding the length of the strips converted to meters: 1.7650 m + 0.8956 m = 2.6606 m.
Hence, the length of the original ribbon is 2.6606 or 2.66 meters.
Metric System Units of Area
The SI base unit for the area is a square meter (m2). Like the metric units of length, the metric units for the area are derived from the base unit (i.e., square meters).
The prefixes you have learned in the metric units for length also apply to metric units for the area. Again, these prefixes indicate that a particular metric unit is a multiple of the base unit.
Six prefixes are used in the metric system, and we list them below together with their equivalent value in the base unit. Note that all metric units for the area have a superscript of 2 to indicate that we are dealing with square units.
| 1 sq. kilometer (km2) | 1000 m2 |
| 1 sq. hectometer (hm2) | 100 m2 |
| 1 sq. decameter (dam2) | 10 m2 |
| 1 sq. meter (m2) | 1 m2 |
| 1 sq. decimeter (dm2) | 0.1 m |
| 1 sq. centimeter (cm2) | 0.01 m2 |
| 1 sq. millimeter (mm2) | 0.001 m2 |
Just like for length, it is easier to visualize these prefixes by using a table:
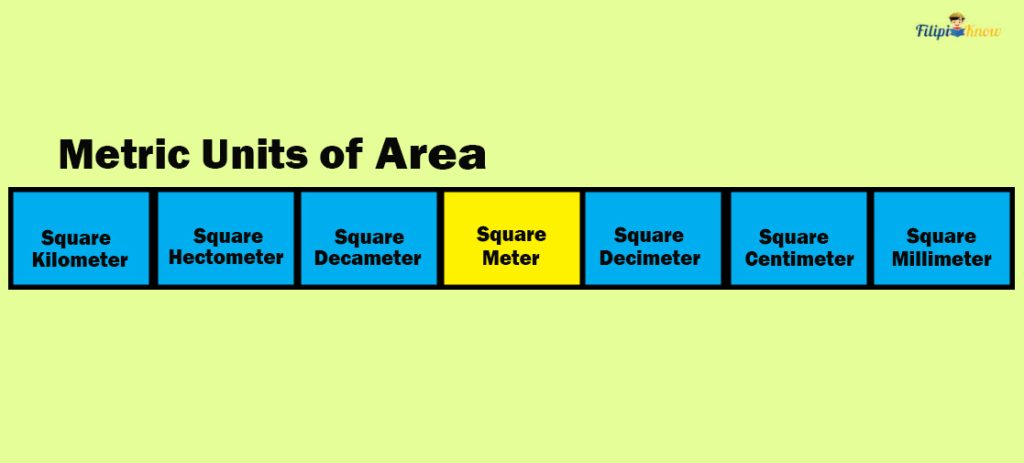
Converting Metric Units of Area
The method of converting metric units of the area is similar to the one we use to convert metric units of length. That is, by moving decimal places.
Let us convert 520 m2 to km2. By looking at the table, there are three steps to the left, from square meters to square kilometers.
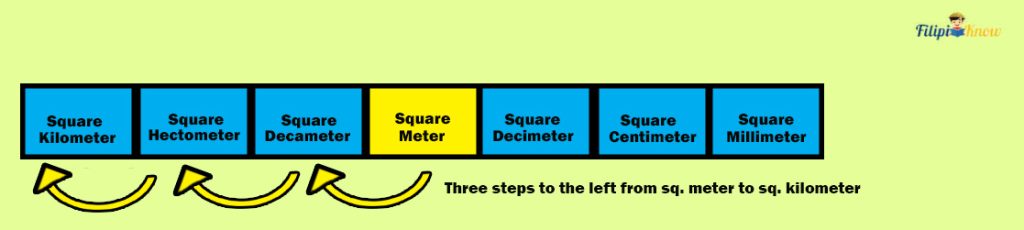
We move three decimal places to the left in 520 m2 to obtain its equivalent in km2.
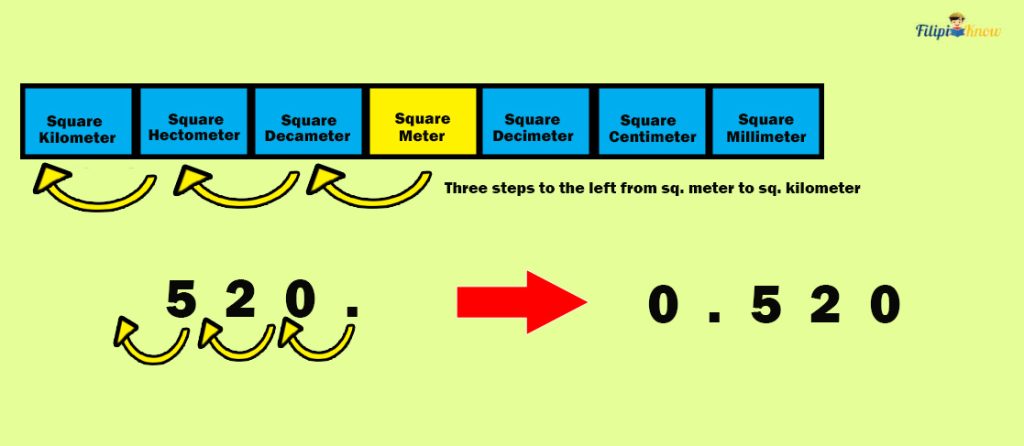
Thus, 520 m2 is equal to 0.52 km2.
Since we always use the table of prefixes of metric units, I highly recommend memorizing the horizontal arrangement of these prefixes. They are not that hard to remember since there are only six prefixes. This is much easier than memorizing the conversion units.
Sample Problem: Every square meter of land in a province costs ₱4,000. Jennie plans to buy a 15-square decameter of land in this province. How much will Jennie have to pay to purchase the land?
Solution: Since the pricing of the land is expressed as ₱4,000 per square meter (m2), we have to convert 15 square decameters (dam2) to square meters (m2) to calculate the land price accurately.
From square decameter to square meter, there’s one step to the right.
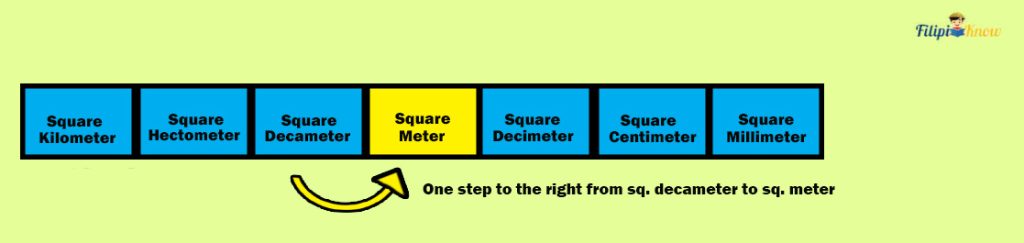
Hence, we move one decimal to the right in 15 dam2 to convert it into m2:
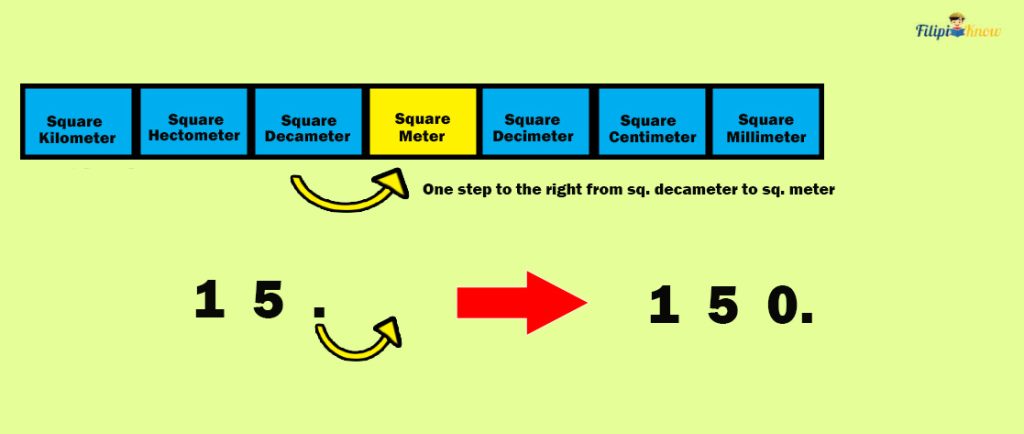
Thus, 15 dam2 is equal to 150 m2.
Now, since the price of the land is ₱4000 per square meter (m2), then a 150 m2 of land will cost:
150 x 4000 = 600,000
The answer is ₱600,000.
Metric System Units of Volume
The SI base unit for volume is cubic meters (m3). Like length, the metric units for volume or capacity are derived from cubic meters (m3).
Six prefixes are used in the metric system, and we list them below together with their equivalent value in the base unit. Note that all metric units for volume have a superscript of 3 to indicate that we are dealing with cubic units.
| 1 cubic kilometer (km3) | 1000 m3 |
| 1 cubic hectometer (hm3) | 100 m3 |
| 1 cubic decameter (dam3) | 10 m3 |
| 1 cubic meter (m3) | 1 m3 |
| 1 cubic decimeter (dm3) | 0.1 m3 |
| 1 cubic centimeter (cm3) | 0.01 m3 |
| 1 cubic millimeter (mm3) | 0.001 m3 |
Just like for length and area, it is easier to visualize these prefixes by using a table:

The liter is another metric unit used for volume/capacity. The liter is a special name for cubic decimeter (dm3). Thus, 1 liter equals 1 cubic decimeter (1 L = 1 dm3).
Like any metric unit, prefixes are also used to derive other metric units for volume. For instance, the prefix “milli” in milliliter indicates that this unit is equal to thousandths (0.001) of a liter.
Although a liter is a metric unit for volume, there’s no need to put a superscript of 3 (which also applies to other metric units based on it).
Here are the other six prefixes associated with liter:
| 1 kiloliter (kL) | 1000 L |
| 1 hectoliter (hL) | 100 L |
| 1 decaliter (daL) | 10 L |
| 1 liter (L) | 1 L |
| 1 deciliter (dL) | 0.1 L |
| 1 centiliter (cL) | 0.01 L |
| 1 milliliter (mL) | 0.001 L |
Again, it’s easier to visualize these prefixes by using a table:

Converting Metric Units of Volume
Converting metric units of volume is similar to converting metric units for length and area.
Sample Problem 1: A shoe box has a volume of 750 cm3. Determine its volume in m3.
Solution: There are two steps to the left from cm3 to m3. Hence, we move two decimal places to the left in 750 cm3 to transform it into m3.

Therefore, 750 cm3 is equivalent to 7.5 m3.
Sample Problem 2: A large tank can be filled with 250 L of water. A water pipe puts 200 cL of water into the tank per minute. How long can the pipe fill the large tank?
Solution: To determine how long the pipe can fill the large tank, we divide 250L by 200 cL. However, we cannot perform this immediately since the given measurements differ in units.
First, let us convert 200 cL to L.
Looking at the table of prefixes, notice two steps to the left from cL to L. Hence, we move two decimal places to the left in 200 cL to convert it into L.
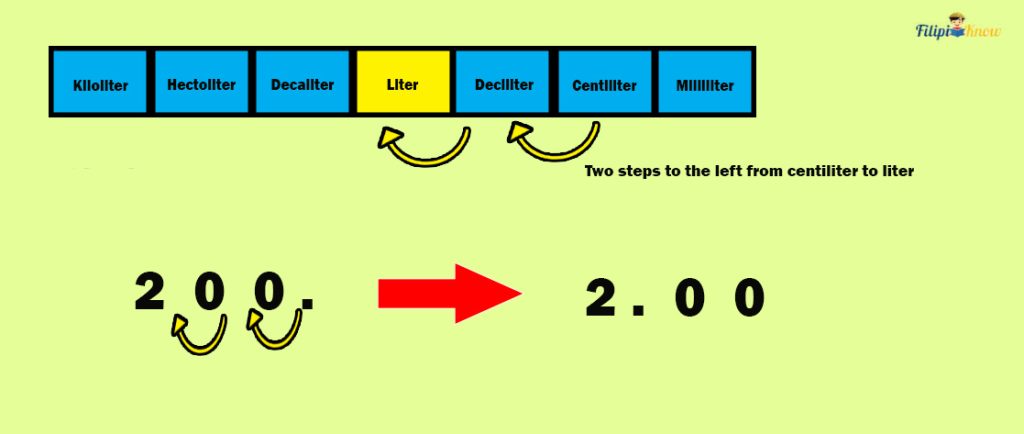
Hence, 200 cL = 2 L
We can now divide 250 L by 2 L. Dividing 250 L by 2 L, we’ll obtain
250 ÷ 2 = 125
This means that the pipe can fill the tank after 125 minutes.
Metric System Units of Mass
The SI base unit for mass is the kilogram (kg). However, note that “gram” is the primary basis for deriving other metric units for mass. “Gram” can be viewed as the “meter” in terms of mass.
Six prefixes are used in the metric system, and we list them here with their equivalent value in the base unit.
| 1 kilogram (kg) | 1000 g |
| 1 hectogram (hg) | 100 g |
| 1 decagram (dag) | 10 g |
| 1 gram (g) | 1 g |
| 1 decigram (dg) | 0.1 g |
| 1 centigram (cg) | 0.01 g |
| 1 milligram (mg) | 0.001 g |
It’s easier to visualize these prefixes by using a table:
Converting Metric Units of Mass
Sample Problem 1: Myrna bought cough syrup with a mass of 50 grams. Determine its mass in milligrams.
Solution: Referring to the table of prefixes, there are three steps to the right from gram (g) to milligram (mg). Thus, we have to move three decimal places to the right to convert 50 g to mg:
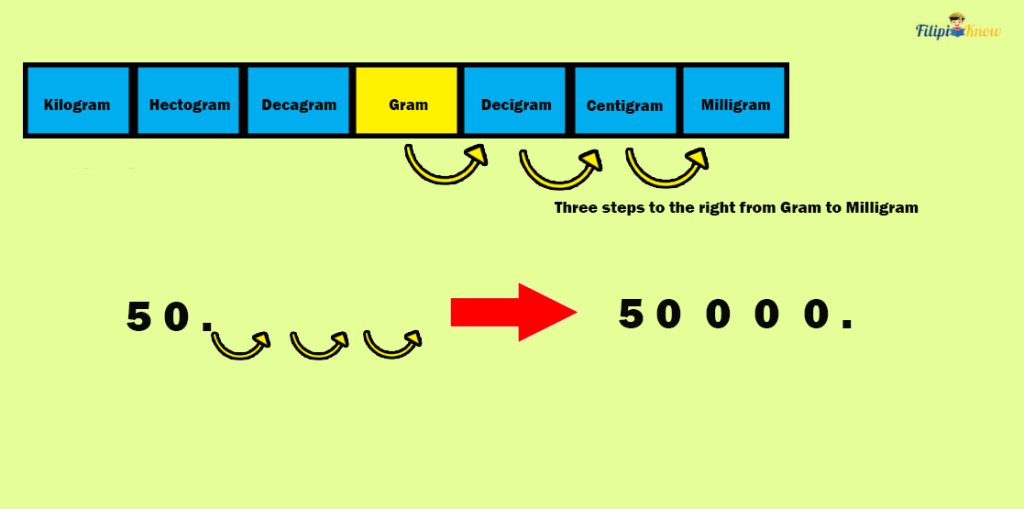
Therefore, the cough syrup’s mass is equal to 50,000 mg.
Sample Problem 2: Rosie bought 1250.50 grams of mangoes. What is the mass of the mangoes that Rosie bought in kilograms?
Solution: Let us convert 1250.50 grams to kilograms. There are three steps to the left, from grams (g) to kilograms (kg). Hence, we must move three decimal places to the left in 1250.50 g to convert it into kilograms (kg).
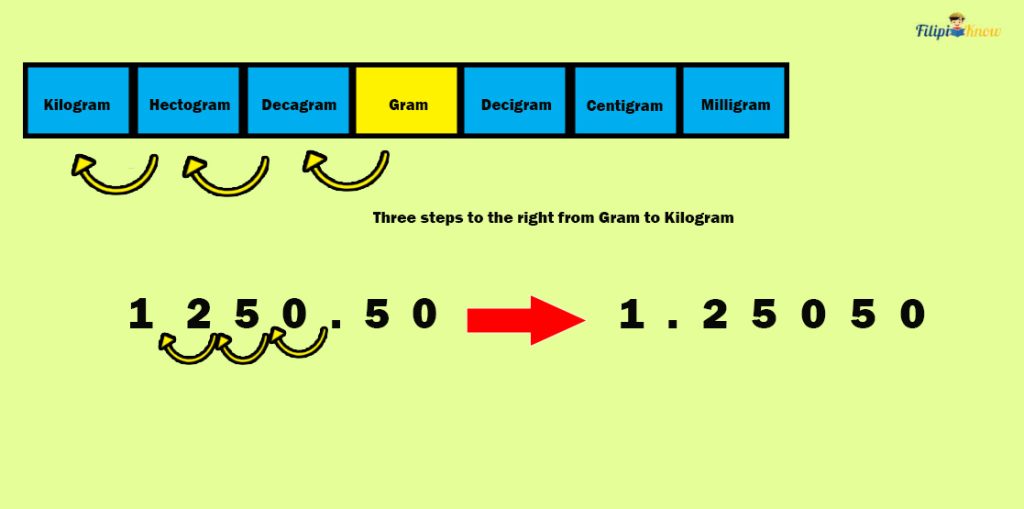
Hence, 1250.50 grams is equal to 1.25050 kilograms.
Converting Units of Time
Let’s now discuss how to convert units of time. Moving decimal places is not applicable for converting time units, unlike the metric units for length, area, volume, or mass. Instead, we have to refer to the conversion values for each unit.
Shown below is the conversion of time units:
| 1 minute | 60 seconds |
| 1 hour | 60 minutes |
| 1 day | 24 hours |
| 1 week | 7 days |
| 1 month | 4 weeks |
| 1 year | 12 months |
| 1 decade | 10 years |
| 1 century | 100 years |
| 1 millennium | 1000 years |
To convert one unit of time to another, follow these steps:
- Identify the given and to which unit we will convert it.
- Determine the relationship between the given units.
- Express the relationship between the given units as a conversion factor in a fractional form such that the denominator has a unit that is the same as the original unit.
- Multiply the given measurement by the conversion factor.
Let us apply the steps above to answer some examples.
Sample Problem 1: How many hours are there in 5 days?
Solution:
Step 1: Identify the given and to which unit we will convert it.
The problem is asking us to convert 5 days into hours.
Step 2: Determine the relationship between the given units.
There are 24 hours in one day. In other words, 1 day = 24 hours.
Step 3: Express the relationship between the given units as a conversion factor in a fractional form such that the denominator has a unit that is the same as the original unit.
In the previous step, we’re able to determine that 1 day is equivalent to 24 hours. Express this as a fraction with the unit that matches the original unit as the denominator. Since the original unit is “days,” we must express the conversion factor as 24 hours/1 day.
Step 4: Multiply the given measurement by the conversion factor.
Now, let us multiply 5 days by 24 hours/1 day:

Hence, there are 120 hours in 5 days.
Sample Problem 2: Rhodora plans to go on a vacation to Lemongate Beach for 8 weeks. How many days will Rhodora be on vacation?
Solution:
Step 1: Identify the given and to which unit we will convert it.
The problem is asking us to convert 8 weeks to days
Step 2: Determine the relationship between the given units.
There are 7 days in one week or 1 week = 7 days.
Step 3: Express the relationship between the given units as a conversion factor in a fractional form such that the denominator has a unit that is the same as the original unit.
In the previous step, we’re able to determine that 1 week is equivalent to 7 days. Express this as a fraction with the unit that matches the original unit as the denominator. Since the original unit is “week,” we must express the conversion factor as 7 days/1 week.
Step 4: Multiply the given measurement by the conversion factor.
Now, let us multiply 8 weeks by 7 days/1 week:

Hence, Rhodora will be on vacation for 56 days.
Sample Problem 3: A worker is paid ₱0.5 per minute for his job. How much will the worker earn if he works for a total amount of time equivalent to 25 days?
Solution: The worker’s wage is expressed as ₱0.5 per minute. Therefore, we must convert 25 days to minutes first before determining the worker’s earnings.
Step 1: Identify the given and to which unit we will convert it.
The problem is asking us to convert 25 days to minutes.
Step 2: Determine the relationship between the given units.
Note that before converting days to minutes, we must first convert days to hours. Afterward, we will convert the result to minutes. This means that we will be dealing with two relationships in this problem.
- Relationship #1 (days to hours): 24 hours in 1 day or 1 day = 24 hours.
- Relationship #2 (hours to minutes): 60 minutes in 1 hour or 1 hour = 60 minutes.
Step 3: Express the relationship between the given units as a conversion factor in a fractional form such that the denominator has a unit that is the same as the original unit.
Express the relationships we derived from Step 2 as conversion factors:
- For relationship #1 (days to hours), the original unit is days, so we have 24 hours/1 day
- For relationship #2 (hours to minutes), the original unit now is hours, so we have 60 minutes/1 hour
Step 4: Multiply the given measurement by the conversion factor.
Multiply the 25 days by the two conversion factors.

Thus, there are 36,000 minutes in 25 days.
Remember, the worker’s wage is expressed as ₱0.5 per minute. If the worker renders 36,000 minutes of work, he will earn 36,000 x 0.5 = ₱18,000.
Sample Problem 4: 504 hours is equivalent to how many weeks?
Solution:
Step 1: Identify the given and to which unit we will convert it.
The problem is asking us to convert 504 hours to weeks.
Step 2: Determine the relationship between the given units.
To convert hours to weeks, we first need to convert hours to days. Afterward, we convert days to weeks. Thus, we will be dealing with two relationships of the unit of time in this problem:
- Relationship #1 (hours to days): 24 hours in 1 day or 1 day = 24 hours
- Relationship #2 (days to weeks): 7 days in 1 week or 1 week = 7 days
Step 3: Express the relationship between the given units as a conversion factor in a fractional form such that the denominator has a unit that is the same as the original unit.
Express the relationships we derived from Step 2 as conversion factors:
- For relationship #1 (hours to days), the original unit is hours, so we have 1 day/24 hours
- For relationship #2 (days to weeks), the original unit now is days, so we have 1 week/7 days
Step 4: Multiply the given measurement by the conversion factor.
Multiply the 504 hours by the two conversion factors.
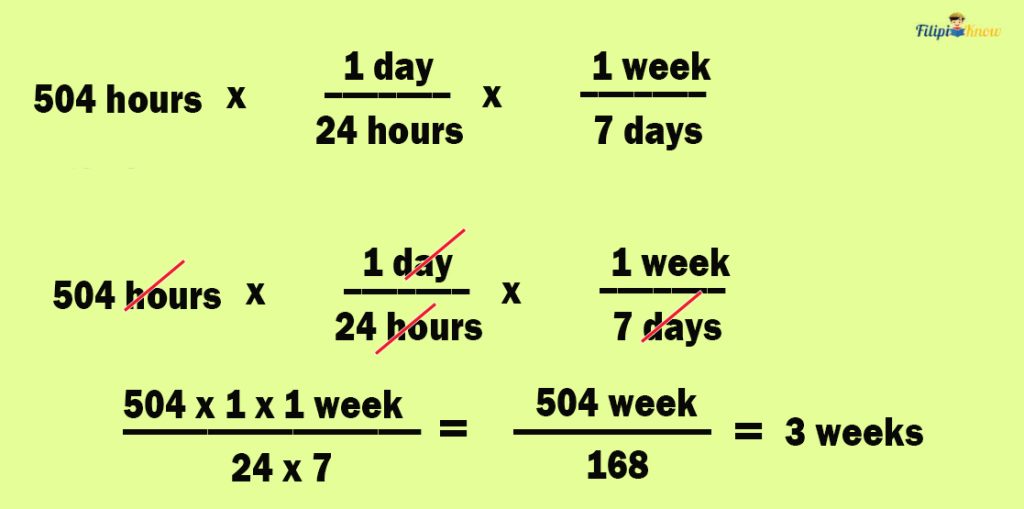
Thus, 504 hours is equal to 3 weeks.
Converting Units of Temperature
Kelvin, Celsius, and Fahrenheit are the units of measurement for temperature. This section will focus only on converting Celsius to Fahrenheit and vice versa.
To convert Celsius to Fahrenheit, use a conversion formula. We will discuss these formulas in this section.
How To Convert Celsius to Fahrenheit
Shown below is the formula to convert Celsius to Fahrenheit:

To use this formula, insert the given temperature expressed in Celsius into the formula and perform the calculation. The resulting value is the equivalent temperature in Fahrenheit.
Sample Problem 1: The freezing point of water is 0°C. What is the freezing point of water in Fahrenheit?
Solution: Applying the formula to convert Celsius to Fahrenheit:
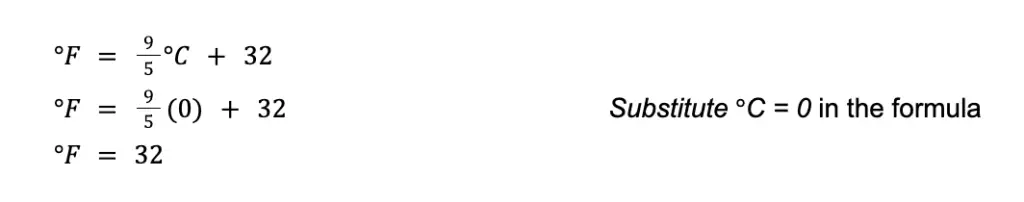
Hence, the freezing point of water in Fahrenheit is 32°F.
Sample Problem 2: The average body temperature is 37°C. What is the average body temperature in Fahrenheit?
Solution: Applying the formula to convert Celsius to Fahrenheit:

Hence, the average body temperature in Fahrenheit is 98.6°F.
How To Convert Fahrenheit to Celsius
Shown below is the formula to convert Fahrenheit to Celsius:

The formula above can be derived using the formula for converting Celsius to Fahrenheit. All you have to do is perform some basic algebra (in particular, solving a linear equation).

To use the formula, insert the given temperature expressed in Fahrenheit into the formula and perform the calculation. The resulting value is the equivalent temperature in Celsius.
Sample Problem 1: Convert 32 °F to °C
Solution:

Hence, 32 °F is equal to 0°C.
Sample Problem 2: The required storage temperature of a particular drug is 59 °F. What is its equivalent in °C?
Solution:

Therefore, 59 °F is equal to 15 °C.
Next topic: Perimeter and Area of Plane Figures
Previous topic: Triangles: Classification and Theorems
Return to the main article: The Ultimate Basic Math Reviewer
Download Printable Summary/Review Notes
Download Printable Flashcards
Test Yourself!
1. Practice Questions [Free PDF Download]
2. Answer Key [Free PDF Download]
3. Math Mock Exam + Answer Key
Written by Jewel Kyle Fabula
in College Entrance Exam, LET, NAPOLCOM Exam, NMAT, PMA Entrance Exam, Reviewers, UPCAT
Jewel Kyle Fabula
Jewel Kyle Fabula graduated Cum Laude with a degree of Bachelor of Science in Economics from the University of the Philippines Diliman. He is also a nominee for the 2023 Gerardo Sicat Award for Best Undergraduate Thesis in Economics. He is currently a freelance content writer with writing experience related to technology, artificial intelligence, ergonomic products, and education. Kyle loves cats, mathematics, playing video games, and listening to music.
Copyright Notice
All materials contained on this site are protected by the Republic of the Philippines copyright law and may not be reproduced, distributed, transmitted, displayed, published, or broadcast without the prior written permission of filipiknow.net or in the case of third party materials, the owner of that content. You may not alter or remove any trademark, copyright, or other notice from copies of the content. Be warned that we have already reported and helped terminate several websites and YouTube channels for blatantly stealing our content. If you wish to use filipiknow.net content for commercial purposes, such as for content syndication, etc., please contact us at legal(at)filipiknow(dot)net
