Permutation and Combination Examples With Answers

Did you know there are about 43 quintillion ways to scramble a 3 x 3 Rubik’s cube?
Yes, that’s a lot! 43 quintillion is larger than the estimated number of stars in the Milky Way Galaxy!
That trivia is astonishing, but how did those mathematicians compute the number of Rubik’s cube combinations? Of course, they did not count every combination since it would take them forever!
What they did was apply the mathematics of permutations and combinations.
Permutations and combinations allow you to identify how many ways you can arrange objects. From arranging people and food selections on the menu to identifying total lock combinations, these two concepts offer a lot of practical applications.
In this review, we’re going to explore permutations and combinations. We will start by studying the concept of factorials, an essential tool for computing them.
Click below to go to the main reviewers:
Table of Contents
Factorial Function
Before proceeding to the concepts of permutation and combination, you must first learn the factorial function.
The factorial function, denoted by “!” (we call it the “factorial sign,” not the exclamation point), tells you to multiply all whole numbers from the given number to one.
For instance, suppose we want to find the value of “7 factorial” or 7! This means we must multiply all numbers from 7 to 1.
7! = 7 x 6 x 5 x 4 x 3 x 2 x 1 = 5040
Therefore, 7! = 5040.
Formally, the n factorial or n! is defined as:
n! = n x (n – 1) x (n – 2) x (n – 3) x … x 1
Sample Problem 1: What is 4!?
Solution: To find 4!, all we have to do is to multiply all whole numbers from 4 to 1:
4! = 4 x 3 x 2 x 1 = 24
Hence, 4! = 24.
Sample Problem 2: What is 5!?
Solution: 5! = 5 x 4 x 3 x 2 x 1 = 120
We can also determine 5! using the value of 4!. Since we have already determined in the previous example that 4! = 24, then we need to multiply 5 by 24 to obtain 5!:
5 x 4! = 5 x 24 = 120

What Is 0 Factorial or 0!?
The definition of factorial of a number is the product of all whole numbers from the given number to one. From this definition, we cannot provide a value for 0!
However, mathematicians have decided to define 0! = 1 for the convention. Although it seems to break logic if we define 0! since 0 is already the smallest whole number, it is necessary to define 0! because it is always encountered in computations involving permutations and combinations.
However, there’s an informal way to define 0!, which you will discover as you go along in this review. But in the meantime, keep in mind that 0! = 1.
Factorial of Negative Numbers and Decimal Numbers
Factorials of negative numbers are undefined, so you can’t encounter such an example with a factorial of a negative number. Meanwhile, to derive the factorial of decimal numbers (or fractions), a special function known as the gamma function is required, but we will not discuss it in this review.
In short, all factorials in this review will only be for whole numbers.
Now that you know what a factorial is, let us start discussing permutations and combinations.
The Fundamental Counting Principle
Suppose you order a drink, a viand, and a type of rice for your lunch in a canteen. The drinks are orange juice, iced tea, gulaman, and water. Meanwhile, the viands available are adobong manok, sinigang na bangus, and menudo. Lastly, the types of rice available are brown rice and white rice. How many possible menu combinations can you create?
To answer the question above, you might try to list all the possible menu combinations like this:
{orange juice, adobong manok, brown rice}
{orange juice, adobong manok, white rice}
{orange juice, sinigang na bangus, brown rice}
…and so on.
Listing all the possible menu combinations will take a lot of your time and energy. Fortunately, a mathematical principle will save us from this tedious task. According to the fundamental counting principle, if there are p ways to do one thing and q ways to do another, then there’s a total of p x q ways to do both.
There are four options to select from if you want drinks for lunch (i.e., orange juice, iced tea, gulaman, and water). Meanwhile, there are three viand options for lunch (i.e., adobong manok, sinigang na bangus, and menudo). Lastly, there are two options to select for the type of rice (i.e., brown and white). Hence, by the fundamental counting principle, the total number of possible menu combinations is
(number of possible drinks) x (number of possible viands) x (number of possible rice types) = number of possible menu combinations
4 x 3 x 2 = 24
Thus, there are 24 menu combinations you can select for your lunch!
Thanks to the fundamental counting principle, it only took us almost a minute to determine the total number of menu combinations. Imagine if we manually listed all the menu combinations; I bet it would take a few minutes to list them all.
Sample Problem 1: Suppose you plan to learn two languages: 1 European language and 1 Asian language. The possible European languages you can learn are French, German, and Italian. Meanwhile, the possible Asian languages are Mandarin and Korean. How many different possible combinations of European and Asian languages can you learn?
Solution: By the fundamental counting principle, the total number of possible combinations of European and Asian languages you can learn is given by:
(number of possible European languages you can learn) x (number of possible Asian languages you can learn)
There are three possible European languages to learn: French, German, and Italian
Meanwhile, there are two possible Asian languages to learn: Mandarin and Korean
3 x 2 = 6
Therefore, the total number of possible combinations of European and Asian languages you can learn is 6.
We can verify our answer by listing all the possible combinations:
| {French, Mandarin} |
| {French, Korean} |
| {German, Mandarin} |
| {German, Korean} |
| {Italian, Mandarin} |
| {Italian, Korean} |
Sample Problem 2: Based on the figure below, how many possible routes can you take to reach City C from City A?
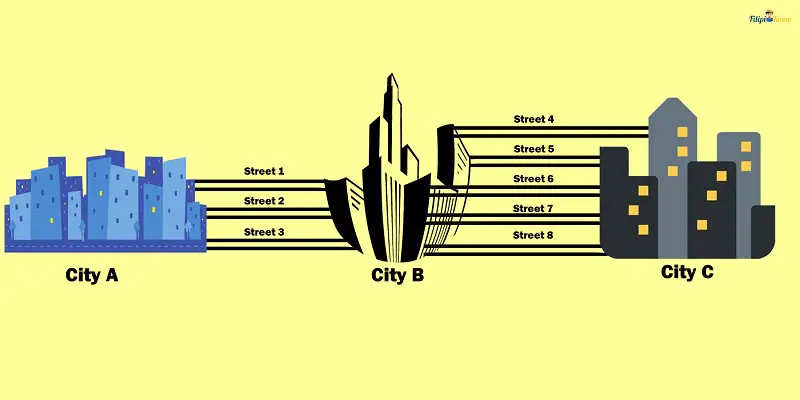
Solution: There are three streets from City A to City B. Hence, there are three ways to go from City A to City B. Meanwhile, there are five streets from City B to City C; hence, there are five ways to go from City B to City C.
By the fundamental counting principle, the total number of possible routes from City A to City C is 3 x 5 = 15.
Remember the fundamental principle of counting and factorials, as they will help you understand the concept of permutations.
Permutations
Suppose you’re thinking of a four-digit password for your cabinet lock. Each digit must be a number from 1 to 9, and no digit must be repeated. What are the possible passwords you can create?
Some possibilities are: 1234, 1324, 2341, 3412, 3142, .. and so on!
Each arrangement of digits that we have formed above is a permutation. The permutations of a set of objects refer to how many times you can arrange these objects. Take note that in a permutation, the order of the arrangement matters.
For instance, in our example above, the permutation 1234 differs from 1324. Although these two arrangements contain the same elements, in a permutation, these arrangements are considered distinct.

Now, suppose ten people participated in a race. How many ways can they be arranged as first, second, and third placers?

The number of ways the ten people can arrange themselves for the top 3 places is an example of a permutation since each combination is distinct. For instance, if Runner 4 wins first place, Runner 2 wins second place, or Runner 8 wins third place, this arrangement is different if Runner 2 wins first place, Runner 8 wins second place, and Runner 4 wins third place.
If the order of the arrangement of the objects does not matter, the arrangements are instead called combinations, which we’ll discuss in the succeeding sections.
Sample Problem: Which of the following is/are example(s) of a permutation?
- Forming three-digit numbers using the numbers 2, 4, 6, 8, and 0.
- Forming a group of three people from these persons: Alexa, Francis, Mac, and John.
- Four people arranged themselves for picture taking.
- Forming a basketball team with 12 players from a group of 35 aspirants.
Solution:
- This is an example of a permutation since each three-digit number you can form using the given numbers are distinct from each other (the order of the arrangement of the digits is essential). For instance, although 246 and 642 are essentially the same digits, these numbers are different or distinct. Hence, these arrangements are counted as two different things.
- No, this is not a permutation. Suppose we form a group consisting of Alexa, Francis, and Mac. Even if we change the arrangement of these persons (e.g., Francis, Mac, and Alexa), we are still referring to the same group. Hence, the arrangement of the objects in this situation does not matter. This example is not a permutation but instead a combination.
- This is an example of a permutation since every time the four persons change their positions in the picture taking, they take different pictures. Although the persons in the picture are the same, the arrangement change makes the “pictures” different. Hence, this is a permutation.
- No, this is not a permutation. If you form a group of 12 players, even if you change the arrangements of the players in the set, they are still referring to the same group. So, the order is not important in this situation. Thus, it cannot be considered a permutation.
How To Find the Number of Permutations
In this section, we will find out how we can determine the number of permutations or arrangements that can be formed from the given objects.
For example, how many three-digit numbers can you form using the numbers 2, 4, 6, 8, and 9?
Again, this is an example of permutation since the order of the arrangement of the objects matter (e.g., arrangement 246 is distinct from 426 and 642).
If we try to list all the three-digit numbers that can be formed using the given numbers, it will take us a lot of time to list them. Therefore, we must apply some mathematical techniques so we don’t have to perform such tedious tasks.
Let the three blanks below represent a three-digit number:
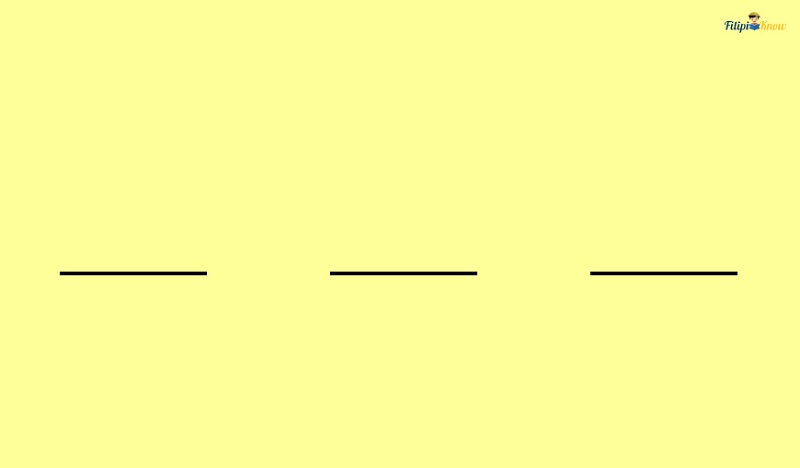
On each blank, we will indicate how many options we have. For the first blank, we have five options – 2, 4, 6, 8, or 9. Note that we can put any of these five options in the first blank, so we put 5 in the first blank.
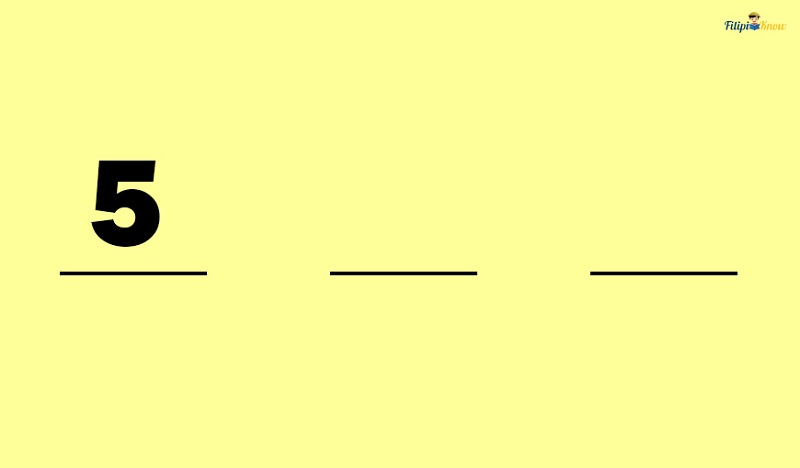
Now let’s move to the second blank. The number of options for the second blank now is only four since we have already filled the first blank with a certain number; thus, we put 4 to the second blank.
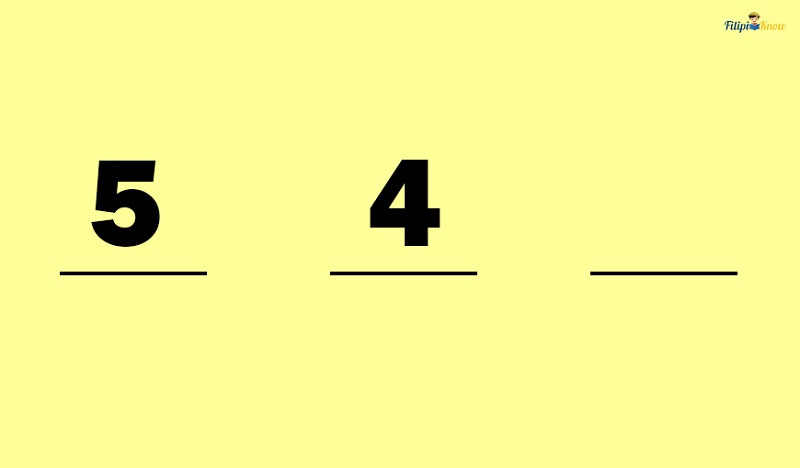
Lastly, there are only three options for the third blank since we have already filled in the two blanks previously. Thus, we put 3 in the third blank.
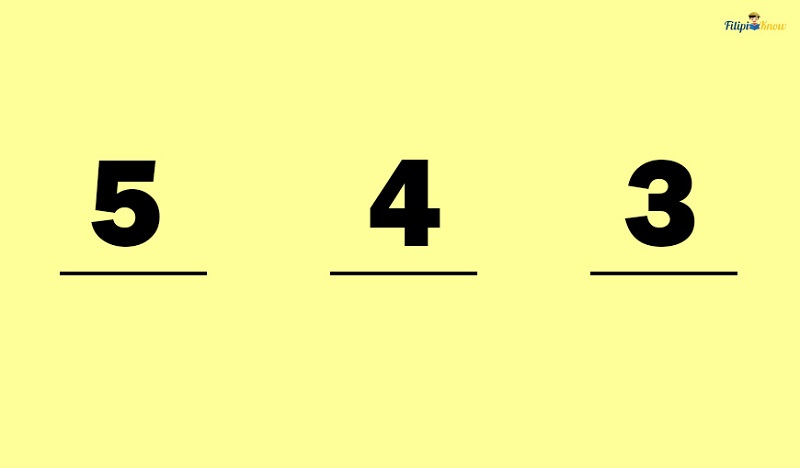
The image above implies five possible numbers for the first digit, four possible numbers for the second digit, and three options for the third digit. We can multiply five by 4 and 3 by the fundamental counting principle.

Therefore, 60 three-digit numbers can be formed using the numbers 2, 4, 6, 8, and 9.
There is another way to find the number of permutations for our problem above, and that is by using a formula. If there are n given objects and you wish to determine how many permutations they can form by arranging r of the given objects at a time, then we can use the formula:
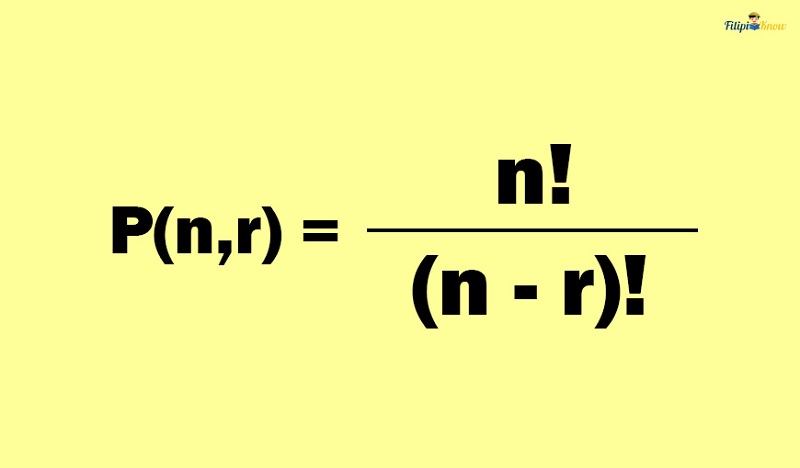
P(n, r) is “the permutation of n objects taken r at a time.” Sometimes, this symbol is written as nPr.
Returning to our example above, let us determine how many three-digit numbers we can form using the numbers 2, 4, 6, 8, and 9.
We have five given objects for this problem, so we have n = 5. We are determining the three-digit numbers that can be formed from these five objects. This implies we are taking three numbers from the five given numbers at a time. So, we have r = 3.
Using the formula, we can determine the permutation of 5 objects taken 3 at a time or P(5, 3):

Here’s a tip: Do not evaluate the factorial as their exact equivalent. Instead, express the factorial in a factored form. For example, instead of writing 120 for 5!, write it as 5 x 4 x 3 x 2 x 1. If we write the factorials in factored form, we can easily simplify them (unlike if they are actual numbers which are much more difficult to compute).
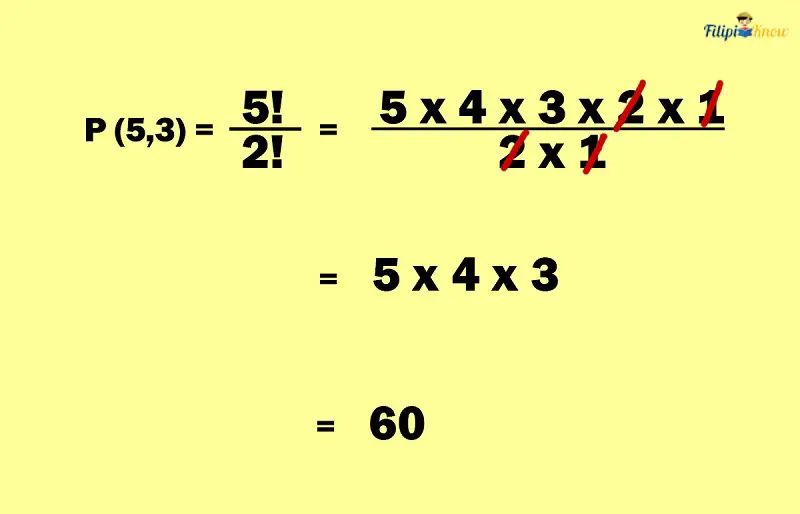
This means that P(5,3) = 60. Hence, the answer to this problem is 60. Sixty three-digit numbers can be formed using the numbers 2, 4, 6, 8, and 9.
Let us solve more permutation problems below.
Sample Problem 1: How many ways can you arrange the letters of the word MATH, taking three letters at a time?
Solution: In this problem, we have n = 4 (MATH has four letters) and r = 3 (since we are taking three letters at a time).
Using the formula for permutation:
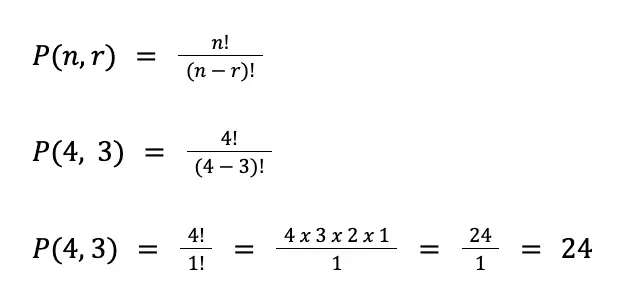
Hence, the answer to this problem is 24.
Sample Problem 2: How many ways can five people arrange themselves for picture-taking?
Solution: In this problem, we have n = 5 (since there are five people given in this problem) and r = 5 (since we are taking all five people at a time).
Using the formula for the permutation:
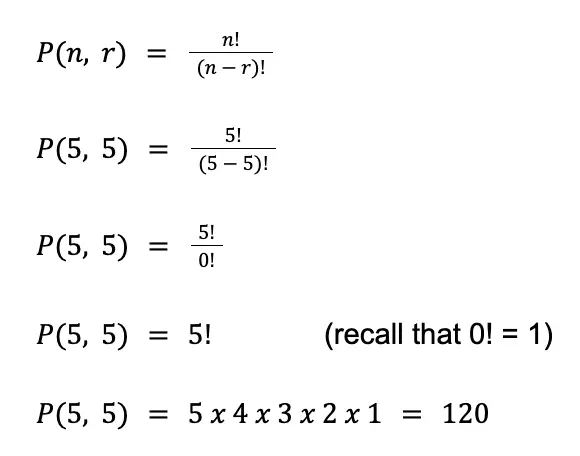
Thus, five people can arrange themselves for picture-taking 120 times.
Distinguishable Permutations
What if some objects in a set are repeated? How are we going to find their permutations?
For example, suppose that we want to find the total number of ways to arrange the letters of the word ASSURE. Notice that one of its elements (the letter “S”) is repeated twice.
Distinguishable permutations refer to the number of ways we can arrange the given objects if some elements of these objects are repeated in the set. In a distinguishable permutation, we count those arrangements as one if they contain the repeated element. For instance, the arrangements ASE (using the first “S”) and ASE (using the second “S”) will count as one only.
Let us determine the distinguishable permutation of the letters of the word ASSURE.
First, let us determine the total number of permutations of the letters regardless of the repeated letter. So, we have n = 6 and r = 6.
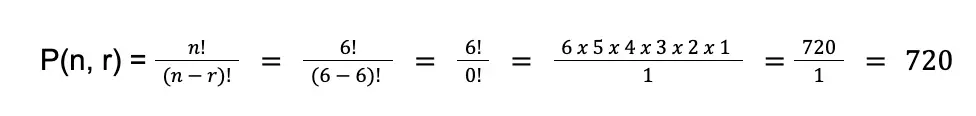
Thus, there are 720 ways to arrange the letters of the word ASSURE. However, in these 720 arrangements, we haven’t considered that an element (letter S) is repeated. Since the element is repeated twice, we need to remove these duplicated elements by dividing the total permutations of 720 by 2! or:
Thus, we have 720/2! or 720/2 = 360.
Thus, the number of distinguishable permutations of the letters of the word ASSURE is 360.
To quickly find the number of distinguishable permutations, we use this formula:

The formula above tells us that the permutation of n objects with a object repeated, b object repeated, c object repeated, and so on can be derived by dividing n! by the product of a!, b!, c!, and so on.
Let us have some examples to help us understand the concept better.
Sample Problem 1: Find the number of distinguishable permutations of the letters of the word BOOK.
Solution: BOOK has four letters, so we have n = 4.
Meanwhile, the letter O is repeated twice, so we have 2! for the denominator of the formula. Thus, the number of distinguishable permutations is PDistinguishable = 4! / 2! or
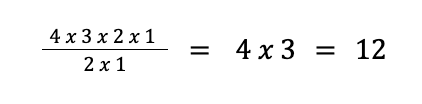
The answer is 12.
Sample Problem 2: How many ways can you arrange the letters of the word MATHEMATICS?
Solution: MATHEMATICS has 11 letters, so we have n = 11.
M is repeated twice, so we have 2! in the denominator of the formula.
A is repeated twice, so we have another 2! in the denominator of the formula.
T is repeated twice, so we have another 2! in the denominator of the formula.
Let us now use the formula:


Hence, there are 4,989,600 ways to arrange the letters of the word MATHEMATICS.
Number of Permutations if Options Can Be Repeated
In our previous sections, we have studied cases of permutation where the options cannot be repeated.
For example, suppose we want to determine how many three-digit numbers can be formed using the numbers 2, 4, 6, 8, and 9. In that case, we don’t count in the number of permutations where the arrangements of elements are repeated as an option. For instance, we haven’t included the arrangements 224, 444, 868, 992, and 464 since these arrangements have numbers that are repeated twice as digits.
If we allow repetition of the elements as options in a permutation, our formula for permutation becomes different. The number of permutations of n objects taken r at a time if repetition is allowed will be defined by the formula:
P(n, r) = n x n x … (r times)
If repetition is allowed, the number of permutations of n objects taken r at a time can be calculated by multiplying n by itself r times.
Sample Problem: If repetition of the digits is allowed, determine the number of three-digit numbers that can be formed using the numbers 2, 4, 6, 8, and 0.
Solution: We have n = 5 and r = 3.
So, we multiply five by itself three times:
P = 5 x 5 x 5 = 125
Thus, the number of three-digit numbers that can be formed if repetition of digits is allowed is 125.
More Examples of Permutation
Let us sharpen your problem-solving skills on permutation through more sample problems below.
Sample Problem 1: A four-digit number password can open a cabinet lock. Each digit must be a number from 1 to 9.
- How many possible four-digit number passwords are there?
- How many possible four-digit number passwords are there if the digits in the password can be repeated?
Solution:
1. We have n = 9 and r = 4. For this situation, we will not include the arrangements where a digit is repeated in the password (e.g., 2233, 1192, 9955, etc.).
We must use

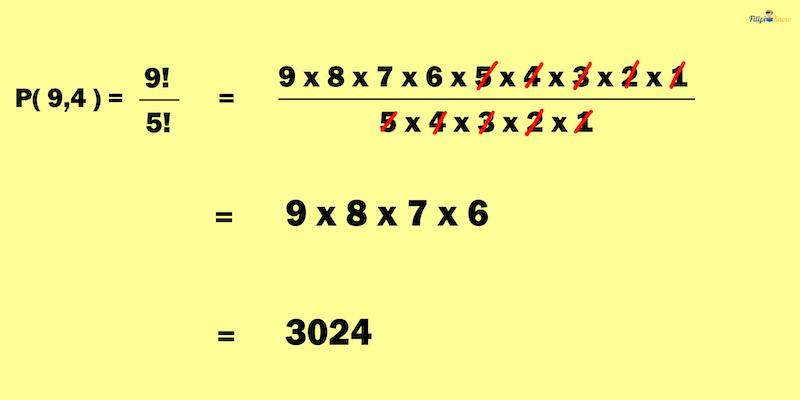
Thus, there are 3,024 possible four-digit number passwords for the cabinet locker.
2. We have n = 9 and r = 4. Since repetition of the digits in the password is allowed, we must use the formula P = n x n x … (r times), or we should multiply nine by itself four times.
P = 9 x 9 x 9 x 9 = 6,561
Thus, if repetition of the digits is allowed, there are 6,561 possible four-digit number passwords for the cabinet locker.
Sample Problem 2: How many ways can four people sit inside a car if only one knows how to drive (assuming the vehicle has four seats)?
Solution: For this case, we have a particular restriction. The problem says that given four people, only one of them knows how to drive.
Let us set up four blanks such that the first blank represents the driver’s seat while the 2nd up to the fourth blanks represent the remaining seats of the car.
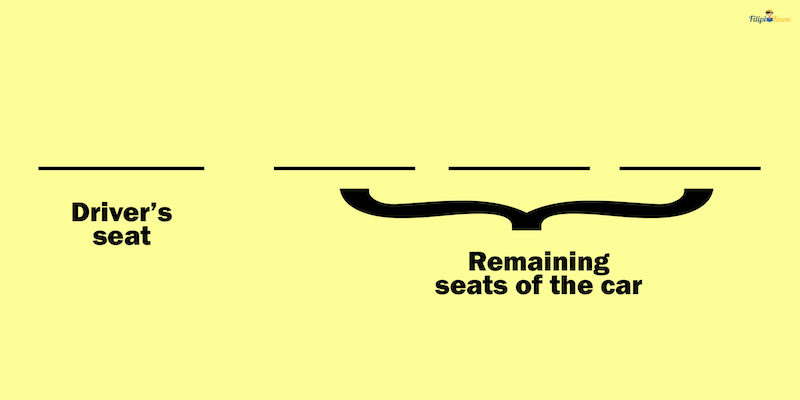
For the first blank, which represents the driver’s seat, there is only one option since only one person among the four knows how to drive. Thus, we put 1 in the first blank.
For the remaining blanks, three people can sit in the three remaining seats differently. In particular, they can arrange themselves in 3! ways so that we can fill the remaining three blanks with 3, 2, and 1, respectively.
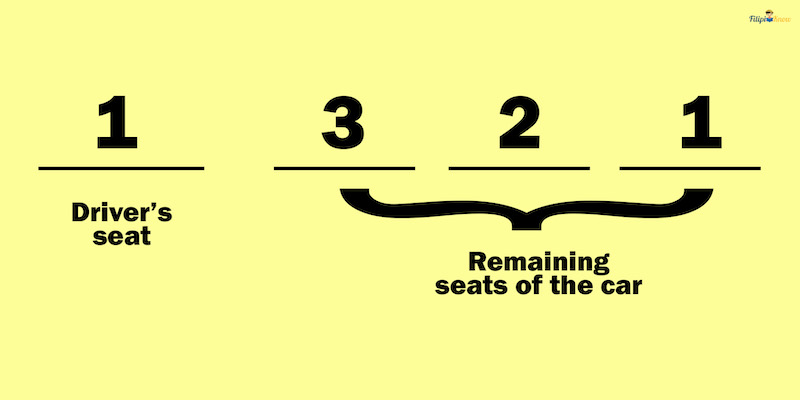
By the fundamental counting principle, 1 x 3 x 2 x 1 = 6.
Thus, the answer to this problem is six ways.
Sample Problem 3: Suppose you have four algebra books and three physics books (all distinct from each other). How many ways can you arrange these books on a shelf if the subjects must be placed alternately?
Solution: This problem has a special restriction again. In particular, we must place the books in a manner where the subjects are placed alternately:
<algebra book> <physics book> <algebra book><physics book>
There are seven books to arrange, so let us set 7 blanks.
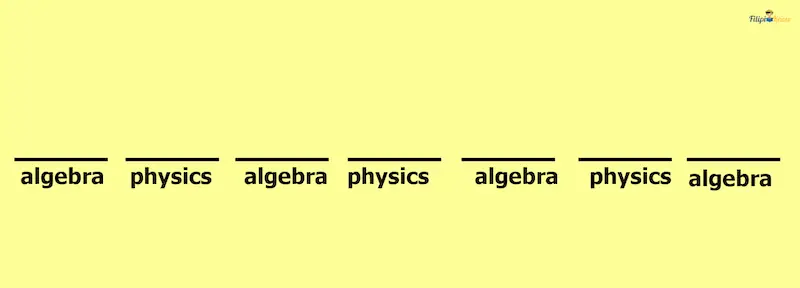
We have indicated under the blank the book’s subject that must be placed on that blank.
On the first blank, there are four options to select (since there are four algebra books), so we place 4 in that blank. For the second blank, there are three options to select (since there are three physics books), so we place 3 in that blank. There are now three options remaining for the third blank since we have already put one algebra book in the first blank; thus, we put 3 in the third blank. There are now two options remaining for the fourth blank since we have already put one physics book in the second blank. We continue this process up to the last blank.

By the fundamental counting principle,
Therefore, the answer to this problem is 144.
Look at the multiplication sentence we have formed: 4 x 3 x 3 x 2 x 2 x 1. Notice that we can rearrange the multiplication sentence as 4 x 3 x 2 x 1 x 3 x 2 x 1, which is simply 4! x 3!. This means we can also solve the given problem by multiplying 4! by 3!.
Combination
Suppose there are five people: Jessie, Alexa, Mac, John, and Alice. How many groups of three people can be formed from these five people?
One possible group we can form is the group made up of Jessie, Alice, and Mac. Note that even if we rearrange the names of these three persons (e.g., Alice, Mac, and Jessie), we are still referring to the same group. Thus, the arrangement of Jessie, Alice, and Mac is the same as that of Alice, Mac, and Jessie. In other words, the arrangement or order of the persons is not crucial in this situation.
If the arrangement or order of the persons or objects is unnecessary, we have a combination.
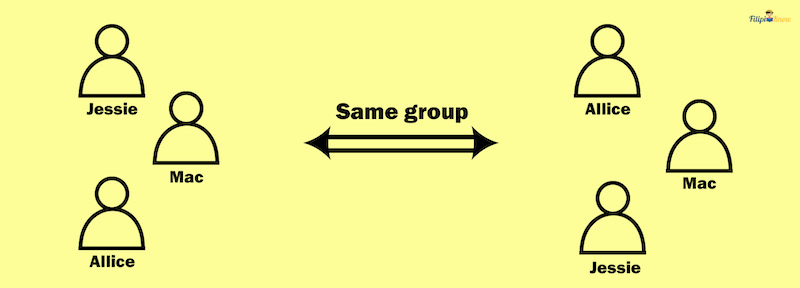
Some common examples are forming a group, a committee, or a team of people. However, there are also examples of combinations that do not involve forming a group, which we will discuss shortly.
Permutation vs. Combination
Let us clarify further the difference between a permutation and a combination. When we say permutation, the order of the arrangement of the objects is essential. Meanwhile, in combination, the order of the arrangement of the objects is not important.
The number of ways ten runners can arrange themselves for first, second, and third place is a permutation since the arrangement order is vital in this case.
Let’s say we have a result such as this:
1st place – runner 1
2nd place – runner 2
3rd place – runner 3
Now if the result turns out as
1st place – runner 2
2nd place – runner 3
3rd place – runner 1
Although the same runners are in the top 3, we still have distinct arrangements. Thus, this situation is a permutation.
However, if we want to form a group of three people from 10 people, we are now dealing with a combination since even if we rearrange the order of the persons in the group, the group is still the same, and nothing changes. In other words, the order of the objects is not necessary here.
How To Find the Number of Combinations
If we want to find the number of combinations that can be formed using n objects taken r at a time, we can use the formula below:
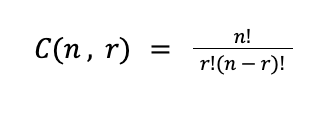
Sample Problem 1: How many groups of three people can be formed from 10 people?
Solution: This situation is a case of combination since even if we change the ordering of the people in a group, the group stays the same, and nothing will change.
We have n = 10 (since ten people are given) and r = 3 (since we are forming a group of 3 people).
Using the combination formula:
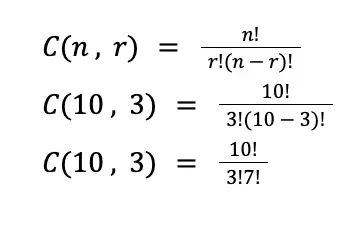

Thus, the answer to this problem is 120 groups.
Sample Problem 2: Given four points on the same plane, how many triangles can be formed?
Let us name the four points in the plane as points P, Q, R, and S.
Solution: One triangle we can form is PQR. Notice that even if we rearrange the letters of PQR, such as QPR or QRP, we still refer to the same triangle, and nothing changes. Thus, this case is an example of a combination.
We have n = 4 (since four points are given) and r = 3 (since three points are required to make a triangle).
Using the formula:
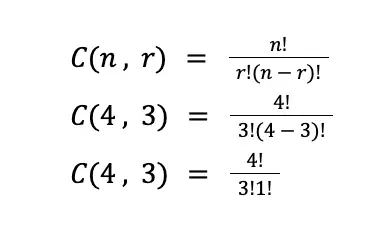
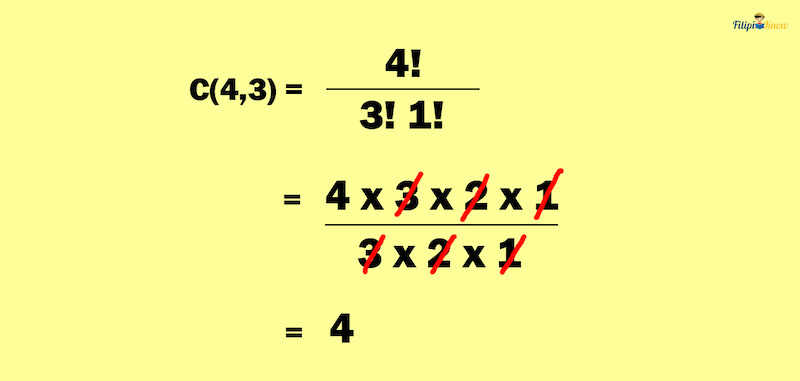
Thus, four triangles can be formed given four points on the plane.
Next topic: Graph Analysis
Previous topic: Probability
Return to the main article: The Ultimate Basic Math Reviewer
Download Printable Summary/Review Notes
Download Printable Flashcards
Test Yourself!
1. Practice Questions [Free PDF Download]
2. Answer Key [Free PDF Download]
3. Math Mock Exam + Answer Key
Written by Jewel Kyle Fabula
Jewel Kyle Fabula
Jewel Kyle Fabula graduated Cum Laude with a degree of Bachelor of Science in Economics from the University of the Philippines Diliman. He is also a nominee for the 2023 Gerardo Sicat Award for Best Undergraduate Thesis in Economics. He is currently a freelance content writer with writing experience related to technology, artificial intelligence, ergonomic products, and education. Kyle loves cats, mathematics, playing video games, and listening to music.
Copyright Notice
All materials contained on this site are protected by the Republic of the Philippines copyright law and may not be reproduced, distributed, transmitted, displayed, published, or broadcast without the prior written permission of filipiknow.net or in the case of third party materials, the owner of that content. You may not alter or remove any trademark, copyright, or other notice from copies of the content. Be warned that we have already reported and helped terminate several websites and YouTube channels for blatantly stealing our content. If you wish to use filipiknow.net content for commercial purposes, such as for content syndication, etc., please contact us at legal(at)filipiknow(dot)net
