Did you know that your odds of being the next multi-millionaire is one to 28,989,675?

Although your chances of winning are minimal, it is not impossible, at least in the eyes of mathematics.

While the probability of you becoming a millionaire is slim, your chances of meeting your special someone randomly is one in 562. 

How are we able to determine the odds of an event happening?

The mathematics of determining quantitatively how likely or unlikely an event will happen is called probability. It is widely used in financial decisions, insurance policies, weather forecasting, assessment of medicinal products, and even in some recreational activities such as gambling or game shows. 

Let us increase your odds of understanding probability and its related concepts through this reviewer.

Click below to go to the main reviewers:

Ultimate Civil Service Exam Reviewer

Ultimate NMAT Reviewer

Ultimate PMA Entrance Exam Reviewer

Ultimate UPCAT Reviewer

Ultimate LET Reviewer

Probability

The probability of an event tells us how likely or unlikely it will happen, but in quantitative form. 

For instance, if you want to tell the possibility that your best friend will get the red card from a deck of playing cards, we can express it descriptively as “My friend will likely get the red card from the deck.” However, the problem with telling these chances descriptively is that it is not precise. 

Instead of just using descriptive words, we can be more specific by saying, “My friend has a 50% chance of getting a red card from the deck.” Look how specific our prediction is if we express it quantitatively. 

So, in probability, we express the likeliness of an event to happen in numerical form, specifically as a fraction, decimal, or percent form. For example, in our example above, the chances of your friend getting the red card from the deck are 50%, 0.50, or ½. 

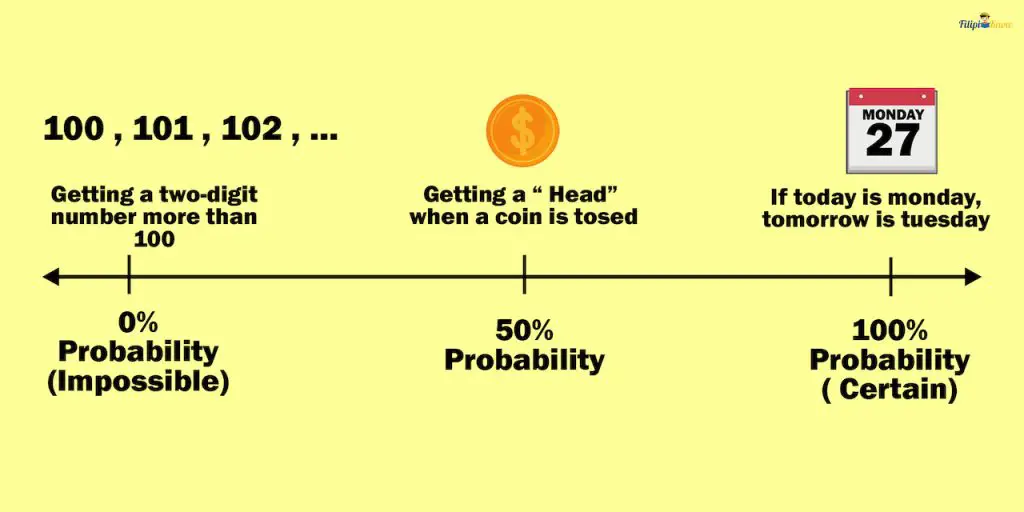
The probability for an event to happen can be expressed as a real number from 0 to 1. If the event will certainly happen or you are completely sure it will happen, its probability is 1. On the other hand, if the event is impossible, whatever the conditions are, then its probability is 0.

For instance, the probability that if today is Monday, tomorrow is Tuesday is 1 or 100%. Meanwhile, the probability that you will randomly get a two-digit number more than 100 is 0 (since all numbers after 100 are more than two digits).

However, the likelihood of most of the events we know to happen cannot be expressed either as 0 or 1. For instance, the odds of getting a head when you toss a coin is 50% or ½,  which is between 0 to 1. We will discuss how to compute the probability of these events shortly.

Now that you have an overview of probability let us define some related terms that will be used throughout our probability study.

Some Terms Related to Probability

Before I teach you how to compute probabilities, let’s first discuss some important terms listed below.

1. Experiment

An experiment is an activity or a procedure that can be done repeatedly with some possible results.

The term “experiment” in probability differs from the “experiment” in the sciences. In probability, the experiment can be any activity regardless of how mundane or trivial.

Tossing a coin is an example of an experiment. Why? Because you can toss a coin repeatedly anytime you want. Theoretically, you can toss the coin infinite times if you desire to. Furthermore, tossing a coin will give you two possible results: a head or a tail. 

Rolling a six-sided die (plural dice) is another example of an experiment since you can perform this event repeatedly. The possible results you can obtain by performing this experiment can be any number from one to six.

Drawing a card from a deck is yet another example of an experiment because you can perform this activity repeatedly. The possible results of this experiment are, of course, the cards in that deck like the “four of hearts,” “king of spades,” “jack of diamonds,” and so on.

Let me clarify that experiments are not just those simple activities mentioned above. It can be as complex as selecting a factory product from a set of newly produced products, obtaining random data from observations, etc.

2. Outcome

An outcome is a possible result of experimenting.

For example, when you toss a coin, getting a “tail” is a possible result, so it is an outcome. Meanwhile, getting a “1” is a possible outcome if you roll a die. If you draw a card from a standard deck, “a nine of spades” is a possible outcome.

Can you think of other outcomes of those experiments we have mentioned above?

3. Sample Space

The sample space is the set of all outcomes of an experiment. If you collected all the possible outcomes of an experiment and put them together into a single set, you will have the experiment’s sample space.

The possible results when you toss a coin is a head and a tail. Note that you only have two possible results for this experiment since a coin only has two sides. Therefore, the sample space of this experiment has two outcomes: head and tail. 

We express the sample space of an event as a set. So, if we write the sample space of the experiment of tossing a coin, we have

S = {Head, Tail}

On the other hand, the sample space for rolling a die is shown below.

S = {1, 2, 3, 4, 5, 6}

When you roll a die, the possible outcomes are 1, 2, 3, 4, 5, or 6 dots. We express these outcomes together as a set, as presented above. Note that the sample space of the experiment of rolling a die has six elements since it has six possible outcomes.

How about drawing a card from a standard deck?

A standard deck has 52 cards, so we expect that our sample space will have 52 elements. If we try to list this experiment’s sample space, it will be incredibly long, so we write it concisely in the form shown below.

S = {Ace_spade, Ace_heart, Ace_diamond, …, King_clover}   n = 52

We indicate an ellipsis (…) to indicate more elements in the set. Meanwhile, we write n = 52 to show that this experiment has 52 possible outcomes.

4. Event

An event is a subset of the sample space of an experiment. Simply put, this is one or more outcomes of an experiment.

For instance, “getting a tail” is an event of the experiment of tossing a coin since it is one of the possible outcomes of an experiment and, thus, a subset of the sample space. 

On the other hand, “obtaining an odd number” is an event of the experiment of rolling a die since it consists of different outcomes, specifically 1, 3, and 5. Note that 1, 3, and 5 are all part of the sample space of this experiment.

“Obtaining a spade” in a deck of cards is an event of the experiment of drawing a card from a standard deck since it consists of different outcomes. Note that you can get “1 of spade,” “2 of spade,” “3 of spade,” “4 of spade,” and so on. These are all components of the sample space of this experiment.

Again, an event can be an experiment’s single or multiple outcomes. “Getting a tail” in a coin toss is an event of a single outcome, while “Getting a spade” in drawing a card is an event of multiple outcomes.

Calculating Probabilities

There are two ways to obtain the likeliness of an event to occur mathematically. We can calculate it using Theoretical Probability or Experimental Probability.

1. Theoretical Probability

Theoretical probability is the one we are more familiar with. In a coin toss, we know that the probability of getting heads is ½ because there is only one face with a head, and the total face of the coin is two. We get their ratio and obtain ½. Nothing complicated.

Notice that we just used our prior knowledge to determine the probability of getting heads in a coin toss and didn’t perform the experiment. Thus, we have computed the probability of getting heads logically and theoretically. Thus, in this sense, we have used theoretical probability.

Theoretical probability is the process of calculating the probability of an event using logical reasoning or a specific formula without conducting an actual experiment. Mathematically, we calculate the theoretical probability of an event by obtaining the number of favorable outcomes and then dividing it by the total number of outcomes.

Going back to the coin-tossing experiment, suppose we want to find the probability of getting heads. Our favorable outcome is a “head” side of the coin; as we know, a coin has only one head. Thus, the number of favorable outcomes of this event is 1.

On the other hand, the total number of outcomes of a coin toss is two since a coin has two sides which you can get from the experiment. So, the total number of outcomes for this event is 2.

Using the formula for theoretical probability: 

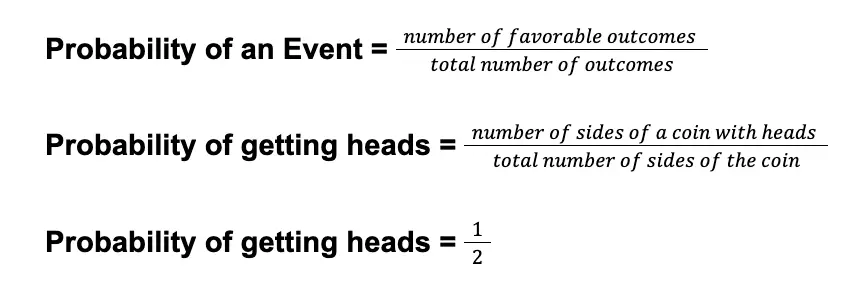
Hence, the probability of getting a “head” in a coin toss is ½. We can also express this answer as a decimal (0.5) or a percentage (50%).

Sample Problems

Sample Problem 1: There are 50 strips of paper in a bowl. Twenty are blue strips, ten are yellow, ten are orange, five are purple, and five are red. Suppose you get one strip of paper from that bowl; determine your probability of getting a red strip.

Solution: The event we are calculating the probability of is “getting a red strip in the bowl.”

The problem states that five red strips of paper are in the bowl. Hence, the number of favorable outcomes is 5.

On the other hand, the total number of paper strips in the same bowl is 50. Hence, the total number of outcomes in this experiment is 50.

Using the formula for theoretical probability:

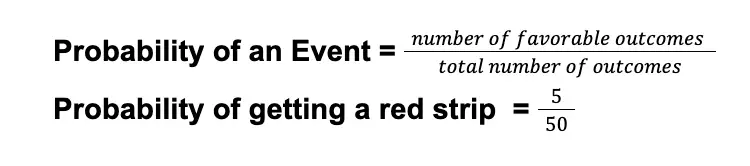
We have obtained 5/50 as the value of the probability. We can simplify 5/50  by dividing the numerator and denominator by their Greatest Common Factor or GCF (i.e., 5).

5/50 ÷ 5/5 = 1/10

Thus, the probability of getting a red strip from the bowl is 1/10. This is equivalent to 0.10 or 10%.

Sample Problem 2: Your mathematics teacher decided to conduct a graded recitation. Your teacher will randomly select a student from your class list who will answer the most challenging question (but with an additional grade incentive). Suppose that the total number of students in your class is 50. What is the probability of you being selected to answer the most difficult question?

Solution: The number of favorable outcomes for you being selected is one since there’s only one “you” in the class. Meanwhile, the total number of outcomes for this experiment is 50 (since there are 50 students that your teacher can choose from).

Using the formula for theoretical probability:

Thus, the probability of you being selected to answer the most challenging question is 1/50. In decimal form, it is 0.02; in percent form, it is 2%. This low probability should give you some relief since you have a tiny chance of being selected. 

Sample Problem 3: What is the probability of getting an odd number if you roll a fair six-sided die?

Solution: Rolling a fair six-sided die (“fair” means all sides have an equal chance of landing up) has a total of six possible outcomes, which are 1, 2, 3, 4, 5, and 6 (we have talked about this earlier).

Among these outcomes, three are odd numbers: 1, 3, and 5. Thus, the number of favorable outcomes for getting an odd number is 3. On the other hand, the total number of outcomes is six since there are six possible outcomes when you roll a die.

Therefore, the theoretical probability of getting an odd number if you roll a fair-six-sided die is

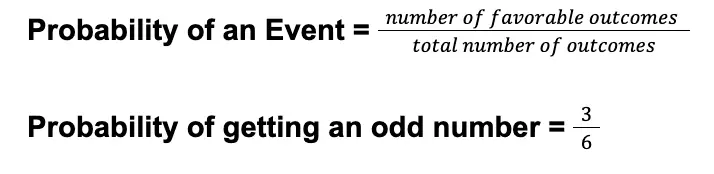
We have calculated a probability of 3/6. Please take note that we can simplify 3/6 into ½.

Thus, the probability of an odd number is ½, 0.5 in decimal, or 50% in percent form.

Sample Problem 4: You will randomly select a card in a standard deck of playing cards. What is the probability of getting a queen?

Solution: As a background, a standard deck of playing cards has:

• Four suites which are spades, clovers, hearts, and diamonds
• Each suite has a king, a queen, and a jack. Therefore, there are four kings, four queens, and four jacks in the deck
• Each suite has an ace. Therefore, there are four aces in the deck (1 for spades, 1 for clovers, 1 for hearts, and 1 for diamonds)
• Lastly, there are 9 number cards in each suite. These cards are numbered from 2 to 10. For instance, we have “2 of spades,” “3 of spades,” “4 of spades,” up until “10 of spades.”

Therefore, a standard deck of playing cards has 52 cards. I have provided these details about playing cards not to encourage you to play poker or whatever card games out there. The reason why we have to talk about these cards is that most of the questions that appear about probability involve a standard deck of playing cards.

We must find the probability of getting a queen in a standard deck. 

As we have stated above, a standard deck of playing cards has four queens, which is one for each suite (i.e., “queen of spades,” “queen of hearts,” “queen of clovers,” and “queen of diamonds”). So, the number of favorable outcomes for this event of getting a queen is 4.

This experiment’s total number of outcomes is 52 (i.e., 52 cards in the deck).

Using the formula for theoretical probability:

Probability of getting a queen = 4/52

The probability we have calculated is 4/52. This is also equivalent to 1/13 in the lowest terms. Therefore, the probability of getting a queen in a standard deck of playing cards is 1/13. In decimal form, it is about 0.08, while in percent, it is about 8%.

Sample Problem 5: What is the probability of getting a pair of numbers with a product of 12 if you roll two fair six-sided dice?

Solution: Let us determine first the total number of possible outcomes for this experiment. In this experiment, you are rolling two fair six-sided dice simultaneously. Rolling one die has six possible outcomes. Therefore, rolling two dice have 6 x 6 = 36 possible outcomes.

Some of these possible outcomes can be 1 for the first die and 2 for the second die; 3 for the first die and 5 for the second die; 5 for the first die and 2 for the second die, and so on. If you write all these possible outcomes or the sample space (the set of all outcomes), you have:

As we have stated, the total number of possible outcomes or pairs of numbers you can obtain is 6 x 6 = 36 pairs. The sample space of this experiment has a total of 36 outcomes.

Thus, we have “total number of outcomes = 36”

Let us now determine the total number of favorable outcomes. The problem asks us to determine the probability of getting a pair of numbers with a product of 12. Going back to the list of possible pairs we have made above, we will see that there are a total of four pairs from the lists with a product of 12 which are: (3, 4), (4, 3), (2, 6), and (6, 2).

This means that the number of favorable outcomes we must use is 4.

Using the formula for theoretical probability:

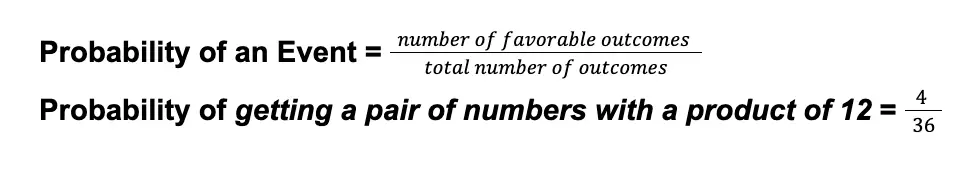
The probability we have calculated is 4/36. This can be simplified as 1/9. Hence, the probability of getting a pair of two numbers with a product of 12 when you roll two dice is 1/9. In decimal form, this is about 0.11. In percent form, it is 11%.

Sample Problem 6: Suppose a computer randomly selects a number from 1 – 100. Determine the probability that the computer will obtain a perfect square number.

Solution: In this experiment, the total number of outcomes is 100 since there are 100 numbers from 1 to 100. 

Since we are interested in determining the probability of randomly selecting a perfect square number from 1-100, the number of favorable outcomes of this event depends on how many perfect square numbers there are from the given range of numbers.

Do you still remember what a “perfect square” number means?

A perfect square number is a number with a whole number square root. This means getting the square root of a perfect square number results in a whole number. 

For example, 36 is a perfect square number because its square root is a whole number (i.e., 6). On the other hand, 15 is not a perfect square number because its square root is not a whole number (approximately equal to 3.87).

Going back to our problem, the perfect square numbers from 1 – 100 are as follows:

1, 4, 9, 16, 25, 36, 49, 64, 81, 100

There are ten perfect square numbers from 1 to 100.

Therefore, the number of favorable outcomes for this experiment should be 10.

Using the formula for theoretical probability:

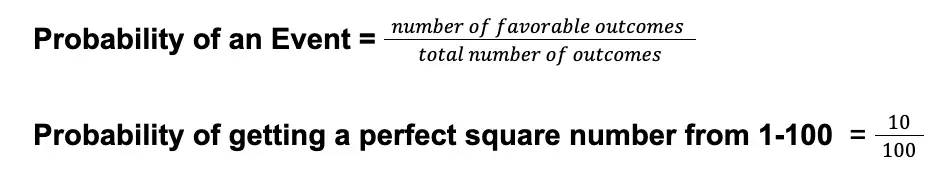
We have calculated a probability of 10/100, equivalent to 1/10 in the lowest terms. Thus, the probability of getting a perfect square number from 1 -100 is 1/10. In decimal form, this is 0.1, and in percent form, this is 10%.

Sample Problem 7: What is the probability of getting spades if you randomly select a card in a standard deck?

Solution: Recall that a standard deck of playing cards has 52 cards. So, the total number of outcomes for this experiment is 52. 

Meanwhile, the total number of spades in the deck is 13 (1 “king of spades,” 1 “queen of spades,” 1 “jack of spades,” 1 “ace of spades,” and nine other numbered spades cards). Hence, the number of favorable outcomes for this experiment is 13.

Using the formula for theoretical probability:

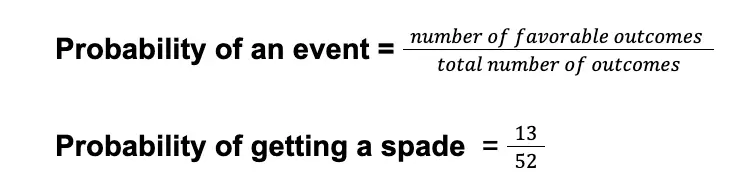
We have calculated a probability of 13/52, equivalent to 1/4 in the lowest terms. Thus, the probability of getting a spade in a standard deck of playing cards is ¼ or 0.25, or 25%.

2. Experimental Probability

Another way of calculating the likeliness of an event happening is through experimental probability. Unlike the theoretical probability we have discussed previously, we experiment with this method and record the outcomes we have obtained. Experimental probability is also known as empirical probability since it is based on experience and data gathered while experimenting.

To determine the experimental probability of an event, we used

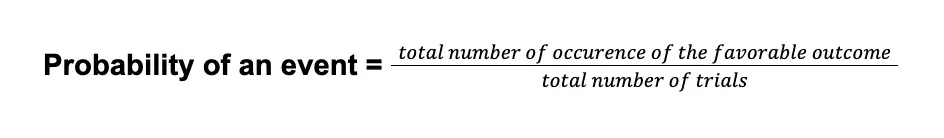
Suppose that, for whatever reason, a person decided to toss a fair coin ten times.  Every time the coin falls, that person records which side of the coin appears. After performing ten trials, the person obtained three heads as the side of the coin. 

The total number of trials in this experiment is ten since the person tossed the coin ten times. Meanwhile, the total number of occurrences of the favorable outcome (which is getting the “head” as the side of the coin) for this experiment is three since it is what the person recorded after performing the coin tossing.

Calculating the experimental probability:

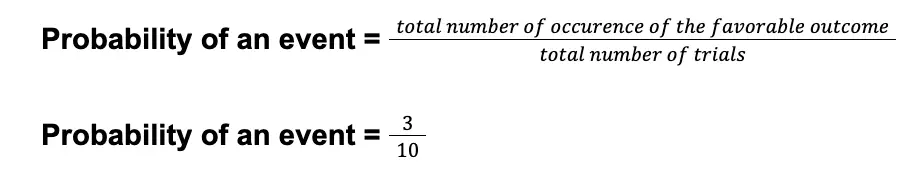
The experimental probability calculated is 3/10 or 0.3 or 30%. Thus, based on the experiment performed by the person in our example, the probability of getting a “head” in his coin tossing is 30%.

Note that the computed experimental probability is oftentimes different from the theoretical probability. As you may recall, the theoretical probability of getting “head” as the side of the coin is ½ or 0.5. However, the experimental or empirical probability can be 3/10 or 0.3 if we experiment, as presented in our example above. But, if you increase the number of trials of the experiment above and record the results, you will notice that as the number of trials increases, the closer the value of the experimental probability becomes to the value of the theoretical probability of an event.

Sample Problems

Sample Problem 1: A bowl has 50 marbles of different colors. Dino takes a marble from the bowl and records the color he obtained. Afterward, Dino returns the marble to the bowl. Dino repeated this process 100 times and found out that he had recorded five blue marbles obtained from the bowl. Based on this experiment, what is the experimental probability of getting a blue marble?

Solution: Based on the example above, the number of trials performed is 100 times since Dino repeated the process of taking marbles 100 times. Meanwhile, since we are interested in determining the probability of getting blue marbles, the number of favorable occurrences of this event is 5 (since Dino obtained five blue marbles from 100 trials).

Using the formula for experimental probability:

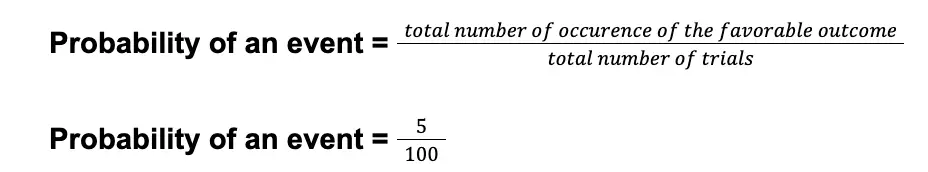
The probability we have calculated is 5/100. This is equivalent to 1/20 in the lowest terms. Thus, the experimental or empirical probability of obtaining a blue marble from the bowl is 1/20, or 0.05, or 5%.

Probability of Various Types of Events

We have learned the two main ways to calculate the probability of an event. However, various types of events require additional techniques to determine their probability of happening. These events include mutually exclusive events, independent events, and conditional events. 

Let us discuss these types of events and how to determine their probability.

1. Probability of Mutually Exclusive Events

Two events are mutually exclusive if they cannot happen simultaneously. For example, when you roll a fair six-sided die, you will get only one side of the die at once. Since you’re only rolling a single die, you cannot get “1” and “2” dots simultaneously. Thus, “getting a 1” and “getting a 2” when you roll a die are mutually exclusive events. 

Another example is that simultaneously living in Manila and Baguio is physically impossible. You can’t be in Manila and Baguio simultaneously since you only have one body; hence, they are mutually exclusive events.

Sample Problem: Which of the following is/are mutually exclusive event(s)?

1. Getting a “head” or a “tail” when you toss a fair coin
2. Getting a “hearts” and a “queen” when you randomly select a card from a deck
3. Going to the 3rd floor and 4th floor of the same building at the same time
4. Randomly selecting an even number and a multiple of 5 from 1 – 100

Solution:

1. These are mutually exclusive events. When you toss a coin, you will never obtain both a “head” and a “tail” simultaneously since only one side of the coin will appear when it falls after you toss it.
2. No, you may get both a “hearts” and a “queen” simultaneously when you randomly select a card. Take note that when you get the “queen of hearts,” you actually both obtain a “hearts” and a “queen” at the same time.
3. Going to the 3rd floor and 4th floor of the same building are mutually exclusive events since you cannot be on the same floor simultaneously (it is physically impossible!).
4. No, you can obtain a number from 1 – 100 that is both an even number and a multiple of 5 simultaneously. For example, if you have selected 20, you have chosen an even number and a multiple of 5 simultaneously.

How To Find the Probability of Mutually Exclusive Events

Probability that both A and B will happen at the same time	P(A and B) = 0
The probability that either A or B will happen	P(A or B) = P(A) + P(B)

1. Probability of Mutually Exclusive Events Happening Both at the Same Time

If A and B are mutually exclusive events, then P(A and B) = 0

As we have stated earlier, since mutually exclusive events cannot happen simultaneously, their probability of happening at the same time is 0 or impossible.

Sample Problem: What is the probability that when you toss a fair six-sided die, you will get both a “3” and a “5” simultaneously?

Solution: Since getting a “3” and a “5” when you roll a die are mutually exclusive events, their probability of happening simultaneously is 0. 

2. Probability of Either One of Two Mutually Exclusive Events To Happen

If A and B are mutually exclusive events, then P(A or B) = P(A) + P(B)

Now, if we are just interested in determining the probability of either of two mutually exclusive events happening, we can derive the probability by obtaining the sum of the respective probabilities of the events.

For example, suppose that we are interested in determining the probability of getting a “3” or “5” when you roll a die; this means that we are not interested in getting the probability of these events happening simultaneously; instead, we are just interested in determining the probability that one of them will happen.

Using our previous example involving the probability of getting a “3” and a “5” (happening simultaneously), we are now interested in the probability of getting either a “3” or a “5” (either of them happens, for instance). 

Take note of the words “and” and “or.” If “and” is used between two mutually exclusive events, then we are interested in the probability of two events happening simultaneously. Meanwhile, if “or” is used between two mutually exclusive events, we are interested in the probability that either will happen (i.e., only one will happen).

Returning to our example, we need to determine the probability of getting either a “3” or a “5” when you roll a die. Again, we need to determine the probability that either of these two events will happen and not the probability of these events happening simultaneously. Furthermore, since “or” is used between the events, we are assured that we are indeed looking for the probability that either will happen.

Let P(3) be the probability of getting a “3” when you roll a fair six-sided die. Meanwhile, let P(5) be the probability of getting a “5” when you roll a fair six-sided die. Lastly, let P(3 or 5) be the probability that you’ll get either a “3” or a “5” when you roll a die.

The probability of either one of two mutually exclusive events happening is the sum of their respective probability. So, we have:

P(3 or 5) = P(3) + P(5)

Let us derive P(3) and P(5).

P(3) is the probability of getting a “3” when you roll a die. So, P(3) =  ⅙ (recall our discussion on theoretical probability).

Meanwhile, P(5) is the probability of getting a “5″ when you roll a die. So, P(5) = ⅙.

Using the computed values we have obtained for P(3) and P(5):

P(3 or 5) = P(3) + P(5)

P(3 or 5) = ⅙ + ⅙

P(3 or 5) = 2/6 

The probability that we have calculated is 2/6. This is equivalent to ⅓ or 0.3, or 30%. 

Thus, the probability that either you will get a “3” or a “5” when you roll a fair six-sided die is ⅓, 0.3, or 30%.

To summarize, if events A and B are mutually exclusive events, then:

• The probability that both A and B happen at the same time is 0: P(A and B) = 0
• The probability that either A or B happens at once is the sum of the respective individual probabilities of A and B: P(A or B) = P(A) + P(B)

Sample Problems

Sample Problem 1: What is the probability of randomly selecting a whole number from 1 to 10 that is a multiple of 3 and 5?

Solution: Randomly selecting a whole number from 1 to 10 that is a multiple of 3 and 5 are mutually exclusive events. Since the word “and” is used between these two mutually exclusive events, we are assured that we must determine the probability of these two events happening simultaneously.

Since the probability of two mutually exclusive events happening both at the same time is 0, then, the probability of randomly selecting a multiple of 3 and 5 from 1 to 10 is 0.

The answer is 0.

Sample Problem 2: What is the probability of randomly selecting a whole number from 1 to 10 that is either a multiple of 3 or 5?

Solution: Since the word “or” is used between these two mutually exclusive events, we are assured that we must determine the probability that either one will happen at once. 

The probability that either one of two mutually exclusive events happens at once is the sum of the respective probabilities of the events. 

P(A or B) = P(A) + P(B)

Let P(multiple of 3) be the probability of getting a multiple of 3 from 1 – 10. Three numbers from 1 to 10 are multiples of 3 (i.e., 3, 6, and 9). Hence, the probability of getting a multiple of 3 from 1 – 10 is 3/10.

Let P(multiple of 5) be the probability of getting a multiple of 5 from 1 – 10. Two numbers from 1 to 10 are multiples of 5 (i.e., 5 and 10). Hence, the probability of getting a multiple of 5 from 1 – 10 is 2/10.

Let P(multiple of 3 or 5) be the probability of getting a multiple of 3 or 5 from 1 – 10. Again, the probability that either one of two mutually exclusive events happens at once is the sum of the respective probabilities of the events. So,

P(multiple of 3 or 5) = P(multiple of 3) + P(multiple of 5)

Using the individual probabilities of the events:

P(multiple of 3 or 5) = 3/10 + 2/10 

P(multiple of 3 or 5) = 5/10

The probability we have calculated is 5/10. This is equivalent to ½ in simplest form. 

Thus, the probability that you randomly select a multiple of 3 or 5 from 1 to 10 is ½ or 0.5, or 50%.

2. Probability of Non-Mutually Exclusive Events

If events can happen simultaneously, then we call them non-mutually exclusive events. These events are the opposite of what we learned in the previous section. For instance, getting a “king” when you randomly draw from a standard deck of cards and getting a “hearts” from the same deck are non-mutually exclusive events since it is possible that when you randomly draw a card, you obtain both a “king” and a “hearts” card (i.e., king of hearts).

Let’s have another example. Suppose that you are randomly selecting a whole number from 1 to 10. The events of “selecting a whole number less than 10” and “selecting a whole number that is a multiple of 2” are non-mutually exclusive since you may obtain a whole number from 1 to 10 that is both less than ten and a multiple of 2 (the number 6, for example). 

How To Calculate the Probability of Two Non-Mutually Exclusive Events

The probability that both A and B will happen at the same time	P(A and B) = P(intersection of A and B)
The probability that either A or B will happen	P(A or B) = P(A) + P(B) – P(intersection of A and B)

1. Probability of Non-Mutually Exclusive Events Happening at the Same Time

Suppose events A and B are not mutually exclusive. In that case, the probability that both A and B are happening simultaneously equals the probability of the intersection of events A and B.

P(A and B) = P(intersection of A and B)

If the word “and” is used between non-mutually exclusive events A and B, then we are assured that we are looking for the probability that both events will happen simultaneously.

To determine the probability that two non-mutually exclusive events will happen simultaneously, we need first to determine the intersection of these two events or what makes A and B not mutually exclusive and then determine the probability for this intersection to happen. 

It may sound complicated, but let us make it easier with the example below.

Sample Problem 1: Jayson will randomly select a whole number from 1 to 10. What is the probability that Jayson selects a whole number that is an even number and a multiple of 3?

Solution: Selecting a whole number from 1 to 10 that is an even number and selecting a whole number that is a multiple of 3 are not mutually exclusive since you may obtain a whole number from 1 to 10 that is both even and a multiple of 3 at the same time (that number is 6).

What is the thing that makes these two events not mutually exclusive? Yes, it’s the number 6 since it is the one that is both an even number and, at the same time, a multiple of 3.

Therefore, 6 is the intersection of the given events. The probability of 6 being selected from 1 to 10 is ⅒. 

Since the probability of two non-mutually exclusive events is equivalent to the probability of their “intersection,” then the probability that Jayson selects a whole number that is even and a multiple of 3 is ⅒. 

There is an easier way to grasp this concept. We can use a Venn diagram for this one.

Let us list all numbers from 1 – 10 that are even: 2, 4, 6, 8, 10. Let us also list all numbers from 1-10 that are multiples of 3: 3, 6, 9.

We create a Venn diagram where two circles intersect; that intersection is the “common” element between the lists we have prepared above:

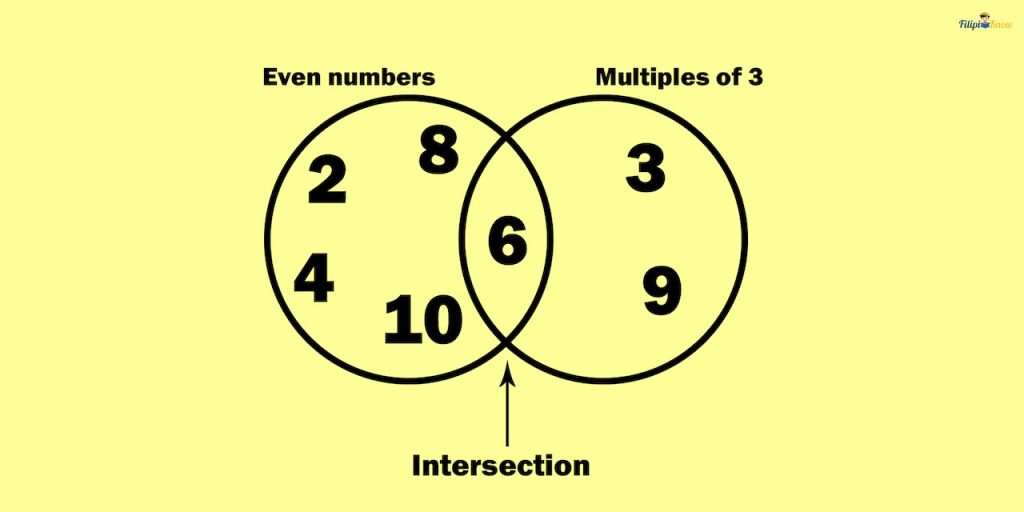
As you can see, the intersection of the events (or sets) is 6. So, we will use it to determine the probability of these non-mutually exclusive events. The probability that six will be selected randomly from 1 to 10 is ⅒. Hence, the answer to the problem is indeed ⅒. 

Sample Problem 2: Suppose 100 strips of paper numbered 1 – 100 are in a bowl. A strip of paper was drawn from the bowl. What is the probability that the strip is numbered with a multiple of 10 and a number larger than 80?

Solution: We are finding the probability that a strip of paper is numbered with a multiple of 10 and, at the same time, larger than 80.

So, we provide a list of the given conditions:

• Multiples of 10 from 1 – 100: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100
• Numbers larger than 80 – 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100

Let us create a Venn diagram to identify the intersection of the lists:

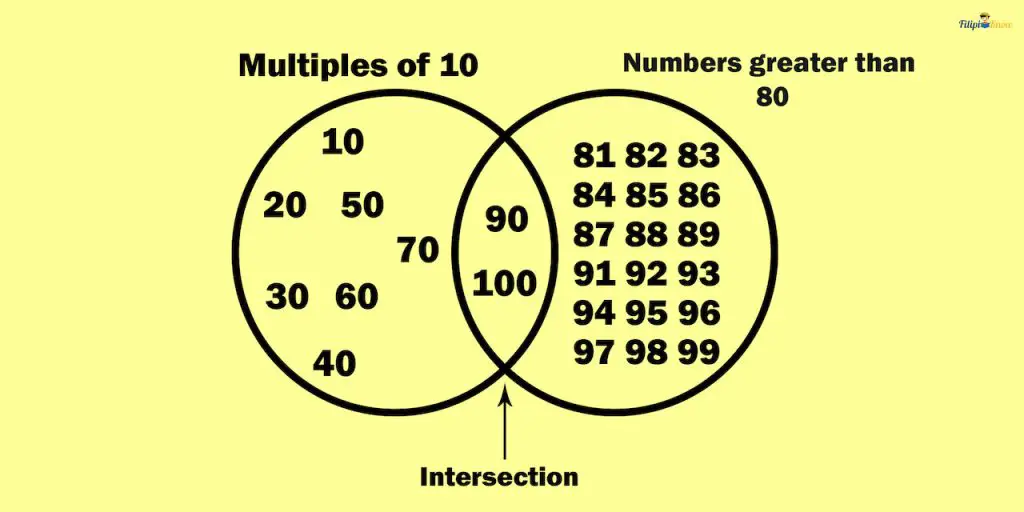
Note that the intersection consists of two numbers – 90 and 100. Note that these numbers are multiples of 10 and larger than 80. 

The probability that the intersections (90 and 100) will be selected in the bowl is 2/100 (since there are 100 slips).

Therefore, the answer to this problem is 2/100 or 1/50 (when simplified). In decimal form, this is 0.02 or 2% in percent form.

2. Probability of Either One of Two Non-Mutually Exclusive Events To Happen

Previously, we have discussed how to compute the probability for two non-mutually exclusive events to happen simultaneously. This time, let us compute the probability that either one of the events will happen. 

If the word “or” is used between two non-mutually exclusive events A and B, then we are assured that we are looking for the probability that either will happen. 

If A and B are non-mutually exclusive events and we want to identify that either one of A or B will happen, then the probability can be calculated using this formula:

P(A or B) = P(A) + P(B) – P(intersection of A and B)

The intersection of A and B is the element that makes A and B non-mutually exclusive or the “common” element.

Let us have some examples.

Sample Problem 1: What is the probability that when you randomly select a number from 1 – 100, the number that will be selected is either an even number or a multiple of 5?

Solution: The events of getting an even number from 1 – 100 and a multiple of 5 from 1 – 100 are non-mutually exclusive since it is possible to obtain a number from 1 – 100 that is both an even number and an odd number (e.g., 10, 20, 30, etc.)

Let us create a list for this one:

• All even numbers from 1 – 100: 2, 4, 6, 8, 10, …, 98, 100
• All multiples of 5 from 1 – 100: 5, 10, 15, 20, 25, …, 95, 100

To identify the intersection of these two events, we think of numbers from 1 – 100 that are both even and a multiple of 5:

Numbers from 1 – 100 that are even and a multiple of 5: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100

Ten numbers are both even and a multiple of 5.

Let A be the event of getting an even number from 1 – 100, and let B be the event of getting a multiple of 5 from 1 – 100.

The probability that either A or B will happen is

P(A or B) = P(A) + P(B) – P(intersection of A and B)

There are 50 even numbers from 1 – 100 (half of these numbers are even, so 50). Thus, P(A) = 50/100.

On the other hand, 20 numbers from 1 – 100 are multiples of 5 (100/5 = 20). Thus, P(B) = 20/100.

Lastly, 10 numbers are both even and a multiple of 5 (we have listed this earlier). Thus, P(intersection of A and B) = 10/100.

Using the formula above:

Thus, the answer is 60/100 or ⅗. This is equivalent to 0.6 in decimal or 60% in percent form.

3. Probability of Independent Events

Two events are said to be “independent” if one of the events has nothing to do with or has no connection to the chances of the other event happening. In simple words, events A and B are independent if A does not influence the probability of B.

When you roll a six-sided fair die, the probability of getting a “3” is ⅙. The probability of getting a “5” on the second try is ⅙. Note that the first try does not influence the probability of getting a “5” on the second try. Hence, getting a “3” on the first try of rolling a die and getting a “5” on the second are independent events. 

Here’s another example. Suppose that there are eight red and seven blue marbles in a jar. Suppose that you randomly picked a marble from the bowl. After picking a marble, you return it to the jar and pick another marble again. If we want to identify the probability that you get a red marble on the first pick and a blue marble on the second pick, these events are considered independent events since the probability of getting a blue marble on the second pick is not affected by the first pick since you returned the marble. 

How To Calculate Probability of Independent Events

The probability of two independent events both happening can be calculated by multiplying the respective probabilities of the events:

P(A and B) = P(A)  x  P(B)

Sample Problem: Suppose a jar has eight red and seven blue marbles. Suppose that you randomly picked a marble from the bowl. After picking a marble, you return it to the jar and pick another marble again. What is the probability that you will get a red marble on the first pick and a blue marble on the second?

Solution: These events of getting a red marble on the first pick and then a blue marble on the second pick are independent since you returned the marble after the first pick.

The probability of getting a red on the first pick is 8/15 (there are eight red marbles out of 15 total marbles).

The probability of getting a blue on the second pick is 7/15 (there are seven blue marbles out of 15 total marbles; the number of marbles hasn’t changed since you returned the marble).

P(red and blue) = P(red)  x  P(blue)

P{red and blue) = 8/15 x 7/15 = 56/225

The calculated probability is 56/225.

4. Probability of Dependent Events

Dependent events are the opposite of independent events. If the first event influences the outcome of the second event and changes its probability, then the events are said to be dependent.

Suppose that there are eight red and seven blue marbles in a jar. Suppose that you randomly picked a marble from the bowl. After picking a marble, you did not return it to the jar and picked another marble again. 

If we want to identify the probability that you get a red marble on the first pick and a blue marble on the second pick, these events are now considered dependent events since the occurrence of the first event (or first picking) will change the outcomes of the second event since there’s now one less marble in the jar.

How To Calculate Probability of Dependent Events

If events A and B are dependent events, then the probability of them both happening is just the product of their respective probabilities:

   P(A and B) = P(A) x P(B)

However, since event A already influenced the probability of event B, we expect that the probability of event B will change.

Sample Problem: Suppose a jar has eight red and seven blue marbles. Suppose that you randomly picked a marble from the bowl. After picking a marble, you did not return it to the jar and picked another marble again. What is the probability that you will get a red marble on the first pick and a blue marble on the second?

Solution: This example is just the example from the previous section about independent events, but this time, the marble you picked on the first try was not returned to the jar. Hence, we expect the probability of getting a blue marble (second event) will change.

The probability of getting a red marble is still 8/15.

Meanwhile, after we picked a marble on the first try, the number of marbles was reduced to 14 (15 – 1 = 14) since we did not return the marble to the jar. Hence, the probability of getting a blue marble for the second pick is now 7/14. Note that if we returned the marble, the probability should have been 7/15, but since we didn’t return the marble, the probability was influenced by the first event and became 7/14.

P(red and blue) = P(red) x P(blue)

P(red and blue) = 8/15 x 7/14 = 56/210

The calculated probability is 56/210. In the lowest terms, this is equal to 4/15. 

As you can see, because of that unreturned marble, the probability of getting a blue marble on the second try drastically changed to 4/15 from 56/225 (the probability if you return the marble).

Next topic: Factorials, Permutations, and Combinations

Previous topic: Measures of Central Tendency

Return to the main article: The Ultimate Basic Math Reviewer

Download Printable Summary/Review Notes

Download Printable Flashcards

Test Yourself!

1. Practice Questions [Free PDF Download]

2. Answer Key [Free PDF Download]

3. Math Mock Exam + Answer Key