Volume of Solid Figures

So far, we have explored the world of one and two-dimensional geometric figures such as lines, angles, and plane figures. This time, we are going to the realm of three-dimensional geometric figures called solid figures.
Objects around you are primarily solid figures. The ice cube you use for your juice, the basketball you dribble, the traffic cone you see on the road, and much more! It will take you forever to list all of them.
This chapter will delve into the world of solid geometric figures such as cubes, cones, pyramids, rectangular prisms, and cylinders. We will also learn how to compute their respective volumes and use this technique to solve real-life word problems.
Click below to go to the main reviewers:
Ultimate Civil Service Exam Reviewer
Ultimate PNP Entrance Exam Reviewer
Ultimate PMA Entrance Exam Reviewer
Table of Contents
What Are Solid Figures?
Solid figures are geometric figures that have three dimensions – width, depth, and height. We live in a three-dimensional world where almost every object is three-dimensional.
Take a look at the given image below. The geometric figure on the left side is a two-dimensional square (i.e., a plane figure). Meanwhile, you see a three-dimensional cube on the right side. Can you see how these figures are different from each other?
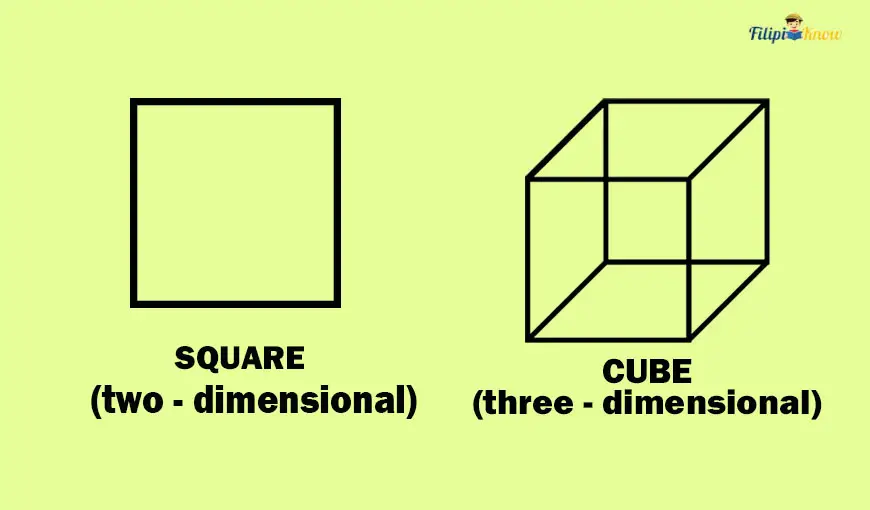
A cube is an example of a solid figure since it is three-dimensional.
In this module, we shift our focus to the branch of geometry that deals with solid figures, the solid geometry.
What Are the Types of Solid Figures?
Let us discuss the most common types of solid figures we can observe in the real world.
1. Cube

A cube is a solid geometric figure with six squares as its “faces.”
The image above shows an example of a cube. Notice that it is made of squares joined together to form this solid figure. These squares are the faces of the cubes. One of the best examples of a cube is the popular puzzle “Rubik’s cube,” which most of us are familiar with.
Other examples of a cube are ice cubes, sugar cubes, and the six-sided dice used in board games.
Since cubes have square faces, the sides of a cube are all congruent or have the exact measurement.
2. Rectangular Prism
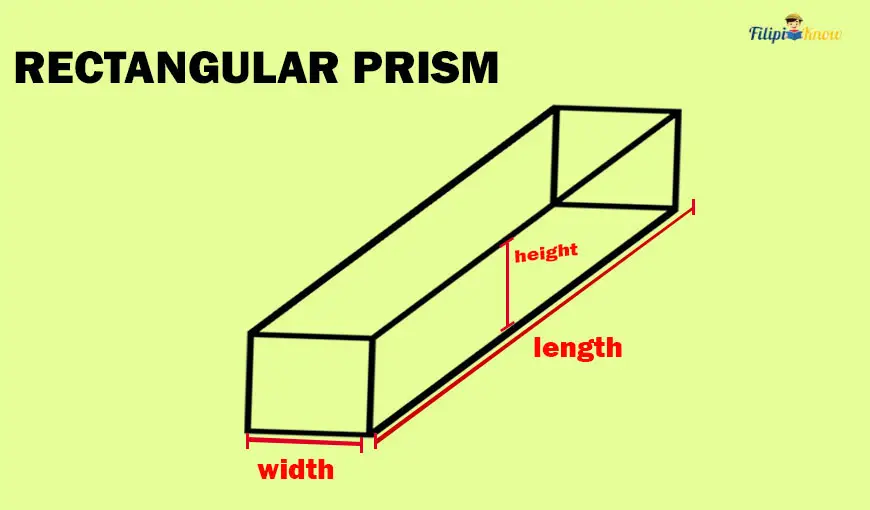
A rectangular prism has six faces, just like a cube. But instead of squares, its faces are all rectangles.
A rectangular prism has length, width, and height. The length of the rectangular prism refers to how long it is, the width refers to how wide or thick it is, and the height refers to how tall it is.
Rectangular prisms are also called cuboids or rectangular solids.
Examples of a rectangular prism are aquariums (or fish tanks), shoeboxes, cabinets, books, cargo containers, and more.
3. Pyramid

A pyramid is a solid figure with triangular sides that meet on a specific point called the apex and a base that is a polygon.
Notice that the square pyramid above has four triangular sides that meet at a certain point (the apex). Its base is a square, so we call it a square pyramid.
The vertical line that connects the base and the apex (topmost point) of the pyramid is the height of the pyramid. In the figure above, the red line represents the height.
If we create such a pyramid with a triangular base, we have a triangular pyramid. Meanwhile, we have a hexagonal pyramid if you use a hexagon as the base. In other words, you can use any polygon as a base to create a pyramid.
The Egyptian Pyramids are a real-life example of a pyramid we are all familiar with. These structures were built thousands of years ago and are considered among the most beautiful creations of ancient human civilizations. In fact, it is regarded as one of the world’s seven ancient wonders.
Other real-life examples of a pyramid include tents and some perfume bottles.
4. Cylinder
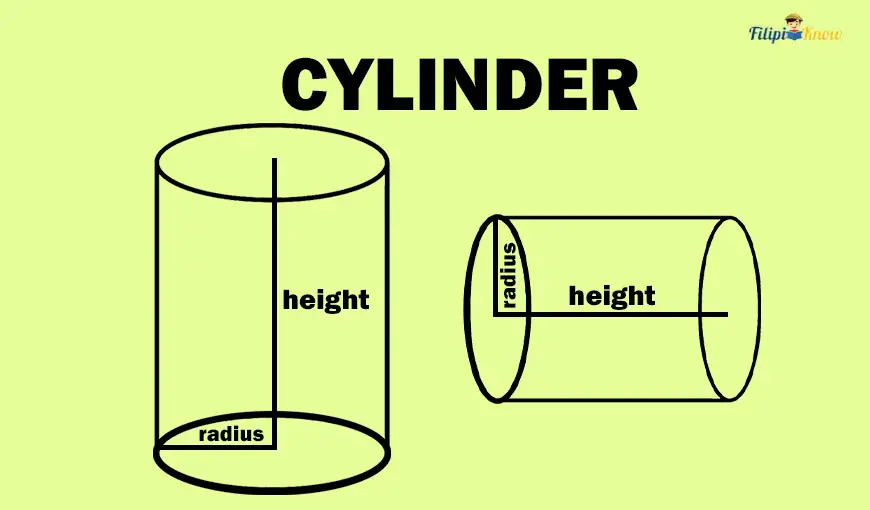
A cylinder is a solid figure with two ends that are congruent circles and parallel. A curved surface connects these circles.
A cylinder has a radius in its circular ends and a height which is the vertical distance from the center of one circular end to another. The height of the cylinder tells you how long (if the cylinder is horizontally placed) or how high (if the cylinder is vertically placed) it is.
One of the best visual examples of a cylinder is a tin can. A tin can has two ends, both circles connected by a curved surface. Aside from tin cans, batteries, cylindrical tanks, drinking glasses, toilet paper rolls, and beakers are some real-life examples of cylinders.
5. Cone
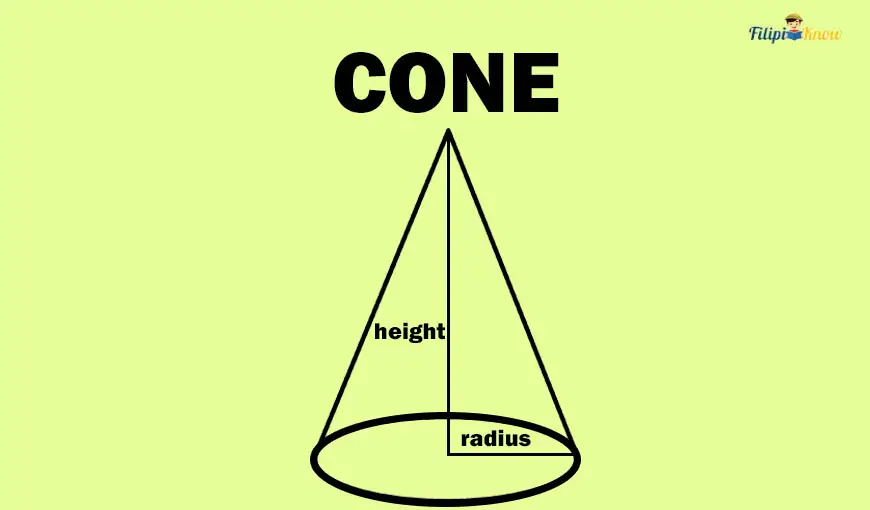
As you can see in the image above, a cone has a circular base connected to the topmost point (called apex) through a curved surface. A cone has a radius in its circular base and a height which is the vertical distance from the apex to the center of the circle.
It is not difficult to imagine a cone in real life since it best resembles the ice cream cone we use for our ice cream. You also see them constantly on the road in the form of traffic cones which help in traffic management. And who can’t forget those conical birthday hats we used to wear during birthday parties?
6. Sphere

The sphere is the solid figure counterpart of a circle. It is the set of all points that are equidistant or have the same distance from a center in a three-dimensional space. In other words, you can think of spheres as solid round figures.
Just like a circle, the sphere has a radius. The sphere’s radius is the distance from the sphere’s center to the point on the sphere. Furthermore, if we form a line segment from one point on the sphere to another and let it pass through the center, we form the sphere’s diameter.
The length of the diameter of a sphere is twice as long as the length of its radius, just like in a circle.
Real-life examples of a sphere include globes we use to represent Earth, the balls we use in outdoor sports such as basketball and volleyball, and those marbles (or jolens) we loved collecting as a child.
There are more solid figures, but we will focus only on these six common solid figures.
Volume of a Solid Figure
The space that a solid figure occupies is its volume.
Think of an aquarium or a fish tank. A fish tank is an example of a solid figure (specifically, a rectangular prism). The maximum amount of water you can put in that fish tank is equivalent to the volume of that tank.
As shown in the image below, you can think of the volume as the number of cubic units you can put inside a solid figure.

However, you cannot see cubic units inside a solid figure in real life. Thus, we must use reliable and accurate methods to determine the volume of solid figures. For this reason, mathematicians derived various formulas to find the volume of these solids.
In this section, let us talk about these methods and formulas.
How To Compute the Volume of Solid Figures
Before calculating the volumes of various solid figures, ensure you have mastered the operations on fractions and decimals because you’ll apply them in the succeeding calculations. If you need to brush up on your manual calculation skills, we advise you to do it first.
Once you are ready, read the succeeding sections to learn how to find the volume of solid figures.
1. Volume of a Cube
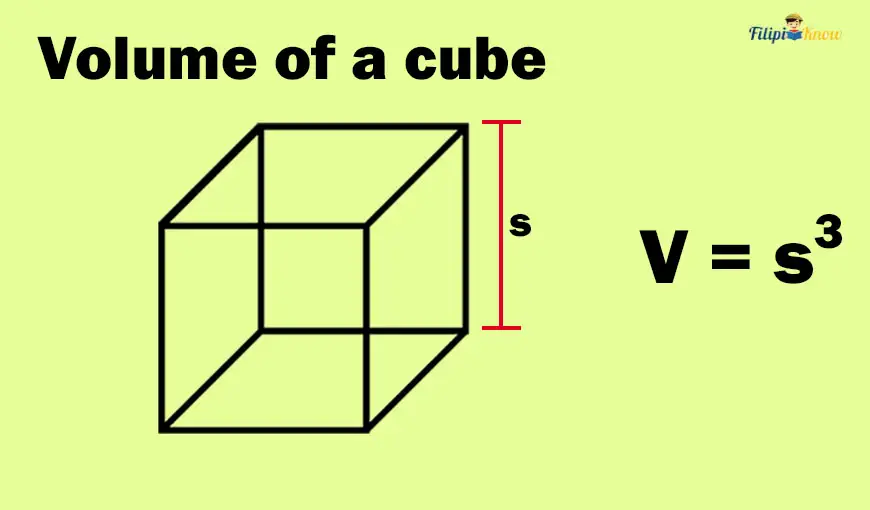
The volume of a cube is just the measurement of the cube’s side multiplied by itself three times. In other words, the volume of the cube can be obtained by raising the length of the side to the third power or by “cubing” it.
In symbols:
Vcube = s3
Quite simple, right?
Sample Problem 1: A cube has a side length of 3 cm. Determine the volume of the cube.
Solution: As we have stated earlier, we can get the volume of this cube just by multiplying the length of the side three times by itself or raising it to the third power.
The given side of the cube is 3 cm long. Therefore, we have s = 3.
Using the formula:
Vcube = s3 = (3)3 = 3 x 3 x 3 = 27
Hence, the volume of the cube is 27 cm3.
Note that when we are writing the volume of a solid figure, we express the given units in “cubic units.” If the given measurement is in centimeters (cm), the volume must be written in cubic centimeters (cm3). Likewise, if the given measurement is in feet (ft), the volume must be cubic feet (ft3).
Sample Problem 2: The packaging used by Lemon Inc. for its lemon-flavored juice drink is cubic. If the side of this cubic packaging material is 15 cm long, how many cubic centimeters of juice drink can be put in the packaging?
Solution: To determine the number of cubic centimeters of juice drink that can be put in the packaging, we must determine its volume. Since the packaging is cubic, we can use the formula for the volume of a cube.
V = s3
The side of the packaging is 15 cm long. Thus, we have s = 15.
Let us substitute s = 15 into the formula:
V = (15)3
V = 15 x 15 x 15
V = 3375
Thus, the volume of the cubic packaging is 3375 cm3. It means about 3375 cm3 of the juice drink can be put in the packaging.
2. Volume of a Rectangular Prism
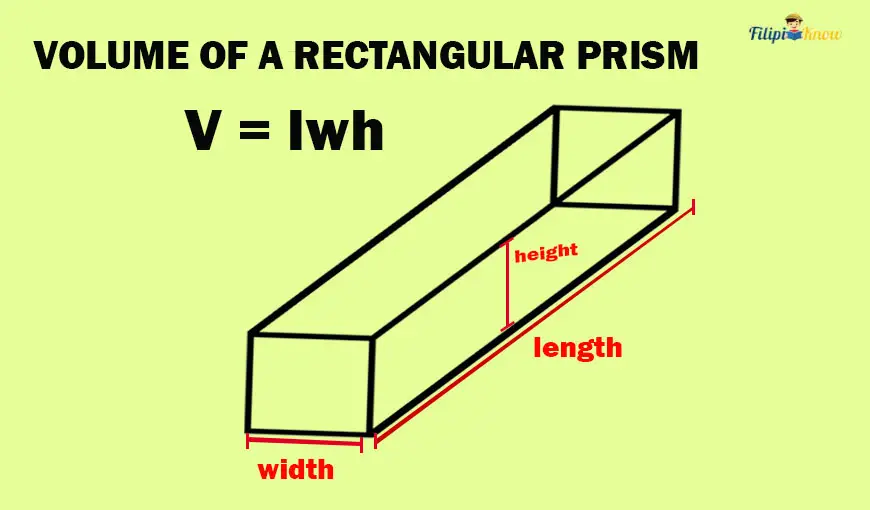
Recall that a rectangular prism has length, width, and height.
Computing the volume of a rectangular prism is quite simple. All you have to do is multiply the rectangular prism’s length, width, and height.
Mathematically,
Vrectangular prism = lwh
where l stands for the length, w for the width, and h for the height of the rectangular prism.
Here are some examples of how to find the volume of a rectangular prism:
Sample Problem 1: What is the volume of a shoebox that is 4 inches long, 3 inches wide, and 3 inches high?
Solution: A shoebox is an example of a rectangular prism. Since we have the shoebox’s length, width, and height, we can compute its volume.
The volume of a rectangular prism is just V = lwh or the product of its length, width, and height.
We have l = 4, w = 3, and h = 3. Using the formula:
V = lwh
V = (4)(3)(3)
V = 36
Thus, the volume of the shoebox is 36 cubic inches (in3).
Sample Problem 2: Compute the volume of the rectangular prism below.

Solution: The given figure above tells us that the length of the rectangular prism is 8 cm, its width is 6 cm, and its height is 5 cm. Recall that the volume of a rectangular prism is just the product of the measurements of its length, width, and height:
V = lwh
V = (8)(6)(5)
V = 240
Thus, the volume of the rectangular prism is 240 cm3.
3. Volume of a Pyramid
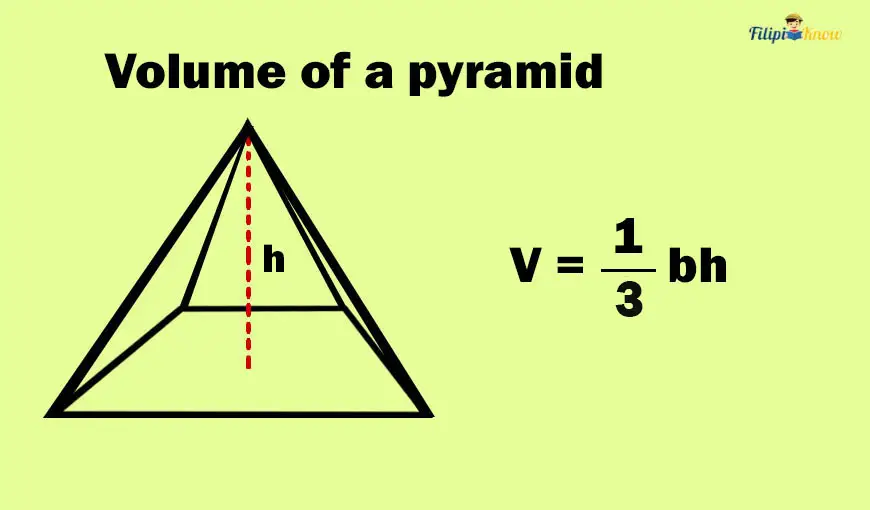
The volume of a pyramid is equivalent to ⅓ of the product of the area of its base and height.
V = ⅓ bh
where b stands for the area of the polygonal base of the pyramid, and h stands for its height.
Most of the time, the height of the pyramid is given. However, the value of the area of the pyramid’s base depends on the base type.
If we have a square pyramid (a pyramid with a square base), then the area of the pyramid’s base is equivalent to the area of the square used as the base. Meanwhile, if we have a triangular pyramid (a pyramid with a triangular base), the area of the pyramid’s base is the area of that triangular base.
Thus, the area of the pyramid’s base is equal to the area of the polygon it uses as the base. To further understand this concept, let us solve some examples.
Sample Problem 1: Determine the volume of the pyramid below:
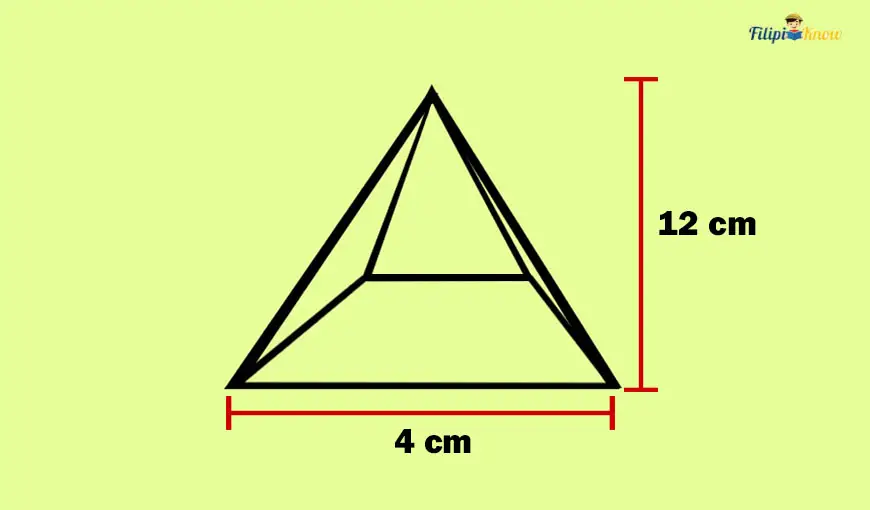
Solution: We have a square pyramid above since the base is a square. The height is already given, which is 12 cm. Meanwhile, the side of the square base is given, which is 4 cm.
Let us determine the area of this square base first to find the volume of this pyramid.
The formula for the area of a square is A = s2. The side of the pyramid’s square base is 4 cm. Thus, we have s = 4.
Therefore, the area of the square is A = (4)2 = 16. Thus, we will use b = 16 as the area of the base in our formula.
We now have base = 16 (as we have computed above) and height = 12 cm (this is given). Let us now do the math and compute the volume of the pyramid:
V = ⅓ bh
V = ⅓ (16)(12)
V = 64
Thus, the area of the square pyramid above is 64 cm3.
Sample Problem 2: A pyramid has a rectangular base. The base has a length of 5 inches and a width of 3 inches. Determine the volume of the pyramid if it is 6 inches tall.
Solution: We already have the height of the pyramid, which is 6 inches. However, we still need to determine the area of the base for us to compute the volume of the pyramid.
How do we find the area of the base of this pyramid?
We have a pyramid that has a rectangular base. Therefore, we need to find the area of that rectangular base.
To clarify, we need to look for the area of the rectangular base so that we can use it in the formula for the volume of the pyramid.
The rectangular base has a length of 5 inches and a width of 3 inches. The area of a rectangle is computed as A = lw or the product of the length and the width. Therefore, the area of the rectangular base is:
A = lw
A = 5(3) = 15 cm2
So, the area of the rectangular base is 15 cm2. We now have a value of b for the formula.
Let us compute the pyramid area using h = 6 (this is given) and b = 15 (as computed above).
V = ⅓ bh
V = ⅓ (15)(6)
V = 30
Therefore, the volume of the rectangular pyramid is 30 cm3.
To make things easier, I will share with you some “specific” formulas that you can use instead to find the volumes of a square pyramid, rectangular pyramid, and triangular pyramid:
| Type of Pyramid | Formula for Volume | Meaning |
| Square Pyramid | Vsquare pyramid = ⅓ s2h | s is the side of the pyramid’s square base, and h is the height |
| Rectangular Pyramid | Vrectangular pyramid = ⅓ lwh | l and w are the length and width of the rectangular base, and h is the pyramid’s height |
| Triangular Pyramid | Vtriangular pyramid = ⅙ (btht)hp | bt and ht are the base and the height of the triangular base, respectively, and hp is the pyramid’s height |
I know that it is taxing to memorize these formulas, so I advise you to stick to the method we discussed earlier: to find the area of the polygonal base first of the pyramid and then compute its volume. However, if you opt to memorize these formulas, there’s no harm in doing it since it takes less time to use these formulas than the long method.
Anyway, let us try to solve the volume of a triangular pyramid using both of these methods:
Sample Problem 3: A pyramid has a base shaped like a triangle. The triangular base has a height of 5 cm and a base of 4 cm. Meanwhile, the pyramid is 10 cm high. Calculate the volume of the pyramid.
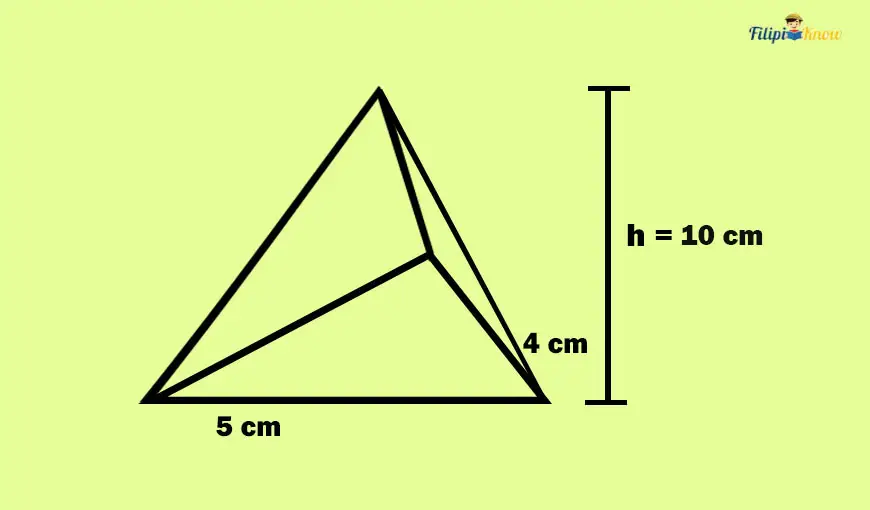
Method 1: Longer Method
Let us compute the area of the triangular base first.
The height of the triangular base is 5 cm while its base is 4 cm. Using the formula for the area of a triangle:
A = ½ bh
A = ½ (4)(5)
A = ½ (20)
A = 10
Thus, the area of the triangular base is 10 cm2.
Now, we have base = 10 and height = 10.
Let us determine the volume of the pyramid using the “general” formula for the volume of a pyramid:
V = ⅓ bh
V = ⅓ (10)(10)
V = 100/3
V = 33.33
Thus, the volume of the triangular pyramid in the problem is approximately 33.33 cm3.
Method 2: Using the “specific formula” for the triangular pyramid
Vtriangular pyramid = ⅙ (bt ht) hp
bt stands for the base of the triangular base. So, we have bt = 4 cm. Meanwhile, ht represents the height of the triangular base. So, we have ht = 5 cm. Lastly, hp represents the height of the pyramid, so we have hp = 10
So, to summarize, we have bt = 4, ht = 5, and hp = 10
Using the formula above:
Vtriangular pyramid = ⅙ (bt ht) hp
Vtriangular pyramid = ⅙ (4)(5)(10)
Vtriangular pyramid = ⅙ (20)(10)
Vtriangular pyramid = ⅙ (200)
Vtriangular pyramid = 200/6
Vtriangular pyramid = 33.33
Thus, the volume of the triangular pyramid is 33.33 cm3.
Notice that you will still arrive at the same answer whether you use the more extended method or the “specific” formula. So, it is up to you which way you prefer.
4. Volume of a Cylinder
The volume of a cylinder is the product of the area of its circular base and height.
In symbols,
Vcylinder = bh
where b is the area of the circular base, and h is the height of the cylinder.
Note that since a cylinder has a circular base, the area of the circular base (b) is b = πr2, where r is the radius of the circular base.
We can make the given formula above more specific:
Vcylinder = πr²h
where r is the radius of the circular base.
You might ask this yourself after looking at the given formulas: Which one should I use?
If the circular base area is already given in the problem, then use V = bh. Meanwhile, if the area of the circular base is unknown and only the radius of the base is given, then use V = πr2h.
Sample Problem 1: The radius of the circular base of a cylindrical tank is 3 meters long. The cylindrical tank is 6 meters high. Determine the total amount of water that can be put in the cylindrical tank (Use π = 3.14).
Solution: The total amount of water that you can put inside the cylindrical tank depends on the volume of that cylindrical tank. So, to answer the given problem, we must compute the volume of the cylindrical tank.
The height of the cylindrical tank is 6 meters. Meanwhile, the radius of its circular base is 3 meters long. Since we have the radius of the circular base rather than its area, we must use the formula V = πr2h.
Let us substitute r = 3 and h = 6 in the formula. Take note that the estimate of π that we are going to use is 3.14:
V = πr2h
V = (3.14)(3)2(6)
V = (3.14)(9)(6)
V = (3.14)(54)
V = 169.56
Thus, the volume of the cylindrical tank is 169.56 m3. This means that the total amount of water that can be poured inside is about 169.56 cubic meters.
Sample Problem 2: The diameter of the circular base of the milk can is 10 cm long. If the can is 14 cm tall, determine the amount of milk that can be put in the can (Use π = 3.14).
Solution: The total amount of milk inside the can depends on its volume.
The circular base of the milk can has a diameter of 10 cm long. Take note that the diameter is twice the measurement of the radius. Thus, if the diameter of the circular base is 10 cm, then the radius of the circular base must be 10/2 = 5 cm.
So, we have 5 cm as the radius of the circular base (r = 5).
Meanwhile, the problem states that the can is 14 cm tall. It means that we have 14 cm as the height of this cylindrical can (h = 14).
Since we already have the radius and height of the cylinder, let us use the formula V = πr2h.
V = πr2h
V = (3.14)(5)2(14)
V = (3.14)(25)(14)
V = 1099
Thus, the volume of the milk can is 1099 cm3. It means that 1099 cubic centimeters of milk can be put inside the milk can.
Sample Problem 3: A clock’s battery is cylindrical. It has a base with an area of 2.5 cm2 and a height of 5 cm. Determine the volume of the clock’s battery.
Solution: The problem provided us with the area of the circular base of the cylinder and its height. Therefore, we can use the formula V = bh.
The given area of the base is 2.5 cm2. So, we have b = 2.5.
Meanwhile, the height of the battery is 5 cm. So, we have h = 5.
Let us now substitute these values for the formula.
V = bh
V = (2.5)(5)
V = 12.5
Thus, the volume of the clock’s battery is 12.5 cm3.
5. Volume of a Cone

The volume of a cone can be calculated as ⅓ of the product of the area of its circular base and height.
In symbols,
Vcone = ⅓ bh
where b is the area of the cone’s circular base, and h is its height.
Since a cone has a circular base, the area of the circular base (b) is b = πr2, where r is the radius of the cone’s circular base.
Hence, we can write the formula above more precisely:
Vcone = ⅓ πr2h
where r is the radius of the circular base of the cone.
As you may have noticed, the formula for the volume of a cone is similar to the formula for the volume of a cylinder. The two solid figures almost have the same formula, except that the cone has an additional ⅓ in its formula. If a cone and a cylinder have the same radius and height, then the volume of the cone is equal to ⅓ of the volume of the cylinder.
Going back to how the volume of a cone is computed, if the area of the circular base and the height of the cone are already given in the problem, use the formula V = ⅓ bh. On the other hand, if only the radius of the circular base is presented and its height, then use V = ⅓ πr2h.
Let us try to solve some examples.
Sample Problem 1: A cone has a base with an area of 120 mm2. If the cone is 50 mm high, determine the volume of the cone.
Solution: In this given problem, the cone base’s area and height are given. Thus, we can use the formula V = ⅓ bh to determine its volume.
So, we have b = 120 and h = 50. Let us calculate the volume of the cone.
V = ⅓ bh
V = ⅓ (120)(50)
V = ⅓(6000)
V = 2000
Hence, the volume of the cone is 2000 mm3.
Sample Problem 2: Determine the volume of the cone below (Use as it is).

Solution: Based on the illustration above, the cone has a defined height of 6 centimeters and a radius of 5 centimeters. Since the cone’s height and radius are already given, using the formula V = πr²h is easier.
We have h = 6 and r = 5. Note that the problem requires us to use π as it is, so we don’t have to use an approximate value and will use the Greek letter instead.
V = ⅓πr2h
V = ⅓π(5)2(6)
V = ⅓π(25)(6)
V = π(25)(2)
V = 50π
Therefore, the volume of the cone is 50π cm3.
Sample Problem 3: Rose has a cylindrical pencil holder and a cone-shaped mini-lamp, which have the same radius (of the circular base) and height. The cylindrical pencil holder has a height of 25 cm and a radius of 10 cm. Determine the volume of Rose’s cone-shaped mini-lamp using the volume of Rose’s cylindrical pencil holder.
Solution: Recall that the volume of a cylinder with the same height and radius as a cone is equivalent to ⅓ of the volume of the cone. Thus, to answer the given problem, we need to find first the volume of the cylindrical pencil holder and then take ⅓ of it to obtain the volume of Rose’s cone-shaped mini-lamp.
Let us first derive the volume of Rose’s cylindrical pencil holder. The problem states that the pencil holder has a height of 25 cm, and the radius of its circular base is 10 cm. Since we have the height and the radius of the circular base, it is more convenient to use the formula V = πr2h for the volume of the cylinder.
We have r = 10 and h = 25. Take note that there’s no estimate of π that we are required to use, so we use it as it is. Substituting these values to the formula:
Vcylinder = πr2h
Vcylinder = π(10)2(25)
Vcylinder = π(100)(25)
Vcylinder = 2500π
Thus, the volume of the cylindrical pencil holder is 2500 πcm3. Now, we need to take ⅓ of the volume of the cylindrical pencil holder to obtain the volume of the cone-shaped mini-lamp. Thus:
Vcone = ⅓ (2500π)
Vcone = 833.33π
Thus, the volume of the cone-shaped mini lamp is 833.33 cm3
6. Volume of a Sphere
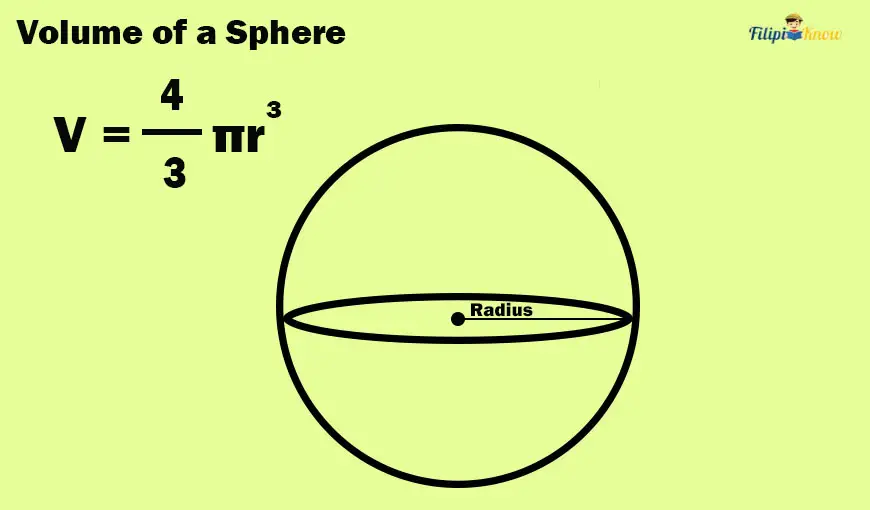
The volume of a sphere can be obtained using the formula below:
Vsphere = 4⁄3πr3
where r is the radius of the sphere.
The formula above is derived by the Greek mathematician Archimedes who also provided one of the earliest estimates of π.
The volume of a sphere can be obtained by multiplying the cube of the sphere’s radius by π, multiplying the result by 4, and then dividing the result by 3.
Sample Problem 1: A ball has a radius of 2 meters. Determine the maximum amount of air that the ball can hold.
Solution: The amount of air the ball can hold depends on its capacity or volume.
The radius of the ball is 2 meters. Thus, we have r = 2.
Note that the problem did not provide us with any approximate value of π that we must use, so we use it as it is.
Using the formula for the volume of a sphere: V = 4⁄3πr3
V = 4⁄3πr3
V = 4⁄3π(2)³
V = 4⁄3π(8)
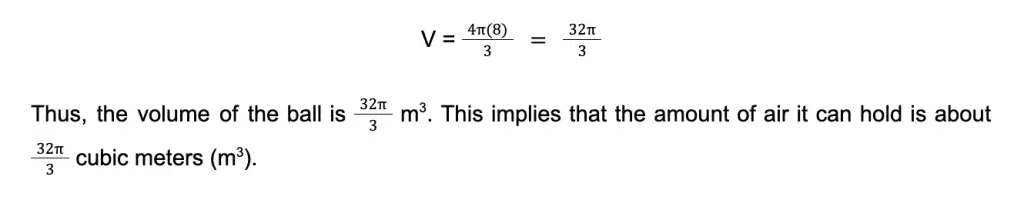
Sample Problem 2: A newly bought globe has a diameter of about 20 inches. Determine the volume of that globe (Use = 3.14).
Solution: The problem is the diameter of the globe which is 20 inches. However, the sphere’s volume formula uses the radius, not the diameter. Thus, we have to determine the radius first.
Recall that the diameter of a round figure, such as a sphere or a circle, is twice as long as the radius. Thus, if the diameter of the globe is 20 inches, its radius must be 20/2 = 10 inches.
Hence, we have r = 10 inches.
Let us now use the formula for the volume of a sphere.
V = 4⁄3πr3
V = 4⁄3(3.14)(10³)
V = 4⁄3(3.14)(1000)
V = 4⁄3(3140)
V = 4186.666…
Thus, the volume of the sphere is 4186.67 cm3.
Next topic: Circles
Previous topic: Perimeter and Area of Plane Figures
Return to the main article: The Ultimate Basic Math Reviewer
Download Printable Summary/Review Notes
Download Printable Flashcards
Test Yourself!
1. Practice Questions [Free PDF Download]
2. Answer Key [Free PDF Download]
3. Math Mock Exam + Answer Key
Written by Jewel Kyle Fabula
in College Entrance Exam, LET, NAPOLCOM Exam, NMAT, PMA Entrance Exam, Reviewers, UPCAT
Jewel Kyle Fabula
Jewel Kyle Fabula graduated Cum Laude with a degree of Bachelor of Science in Economics from the University of the Philippines Diliman. He is also a nominee for the 2023 Gerardo Sicat Award for Best Undergraduate Thesis in Economics. He is currently a freelance content writer with writing experience related to technology, artificial intelligence, ergonomic products, and education. Kyle loves cats, mathematics, playing video games, and listening to music.
Copyright Notice
All materials contained on this site are protected by the Republic of the Philippines copyright law and may not be reproduced, distributed, transmitted, displayed, published, or broadcast without the prior written permission of filipiknow.net or in the case of third party materials, the owner of that content. You may not alter or remove any trademark, copyright, or other notice from copies of the content. Be warned that we have already reported and helped terminate several websites and YouTube channels for blatantly stealing our content. If you wish to use filipiknow.net content for commercial purposes, such as for content syndication, etc., please contact us at legal(at)filipiknow(dot)net
