At the heart of calculus are derivatives. 

The process of taking the derivative of a function is called differentiation. With differentiation, various insights and information were extracted and became part of our current understanding of the study of physics, computer science, economics, statistics, business analytics, and other related fields. 

In this review, you will learn what it means to take the derivative of a function and how to derive it. Furthermore, you will understand the intuition behind derivatives using your prior knowledge of slopes and limits already discussed in the previous reviewers. 

Click below to go to the main reviewers:

Ultimate LET Reviewer

Ultimate UPCAT Reviewer

An Overview of the Derivative of a Function

The derivative of a function f(x) is its rate of change with respect to x. In other words, the derivative of the function tells how sensitive or fast the dependent variable f(x) or y changes with respect to the changes to the value of its independent variable or x. 

Consider the linear function f(x) = 2x + 4. The derivative of this function is 2 (we will discuss later how to get the derivative). This value of the derivative (2) means that f(x) is increasing two times as fast as x. 

To show this, let x = 1. With this value, the value of f(x) will be:

f(1) = 2(1) + 4 = 6

Suppose we change the value of x = 1 to x = 2. Take a look at what will happen to the value of f(x):

f(2) = 2(2) + 4

f(2) = 4 + 4 

f(2) = 8

From x = 1 to x = 2, the “change in value of x” is 2 – 1 = 1. Meanwhile, from f(1) = 6 to f(2) = 8, “the change in value of f(x)” is 8 – 6 = 2. Notice that the change in the value of f(x) is twice as fast as the change in the value of x. This tells us that f(x) changes its value twice as fast as the changes in the value of x. For this reason, the derivative is 2. 

For linear functions, the value of the derivative is a constant. This means that for any values of x, you will always get the same rate of change of f(x) with respect to x. Going back to f(x) = 2x + 4, the rate of change of f(x) with respect to x is always the same regardless of the value of x you will use. 

Earlier, we tried to test how fast f(x) changes if we start from x = 1 and change its value to x = 2. We found out that the value of f(x) changes its value twice as fast as x (the value of f(x) changes from 6 to 8). 

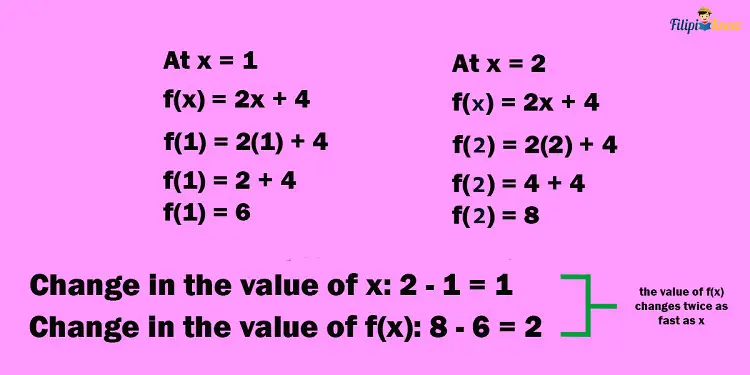
Let us try to use x = 3. Substituting this value to f(x) = 2x + 4. We have:

f(3) = 2(3) + 4 

f(3) = 10

Now, if we change the value of x = 3 to x = 20, we have:

f(20) = 2(20) + 4

f(20) = 44

The change in the value of x, in this case, is from 3 to 20, which is equal to 20 – 3 = 17

The change in f(x) in this case is from 10 to 44, which is equal to 44 – 10 = 34

Surprisingly, the change in the value of f(x) is still twice as fast as the change in the value of x. Hence, the rate of change of f(x) = 2x + 4 with respect to x using the above is still 2. This is what we mean that the derivative of a linear function is a constant value.

However, for those functions that are not linear, the derivative is also a function. For instance, the derivative of f(x) = x² is 2x. 2x is an example of a derivative function. Note that 2x is not a constant. This means that the rate of change of f(x) = x² is not a constant value but depends on what value of x is used. 

Anyway, we will not go deep with the concept of derivatives as it is too complicated. Our goal here is to provide you with an overview so that you have an idea of what the derivative of a function tells us. 

Again, the derivative tells us how fast the value of f(x) changes with respect to x. The derivative of a linear function is a constant, but for nonlinear functions, it depends on the specific value of x used for the derivative function. 

Another way to explain derivatives is through geometric representation. The derivative of a function is also the slope of the line that is tangent to the curve or the graph of the given function. In the image below, the curve is the geometric representation of the function f(x), and the slope of line l₁, which is tangent or intersects the function at a point, is the function f(x) derivative. 

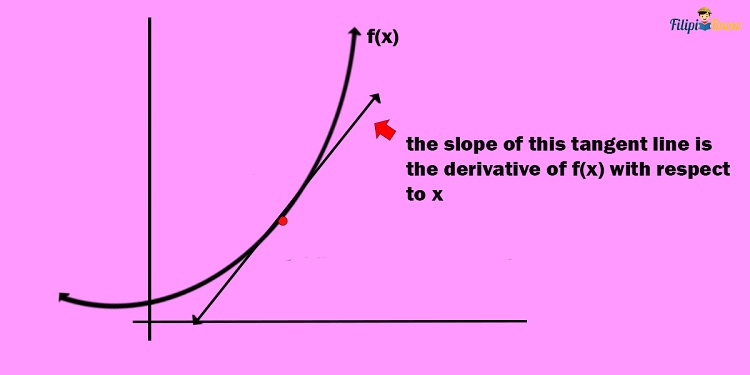
We will not deal too much with the geometric interpretation of the derivative since it is more complicated (and given that we can calculate the derivative without knowing it). If you are interested in how derivatives can be explained using this method, refer to the BONUS section of this article. 

In the meantime, you can proceed to the next section of this review, which deals with the notations used for the derivative of a function. 

Derivative Notations

There are different ways to write the derivative of a function. However, in this section, we are going to discuss only two notations that are commonly used.

The first notation is the Lagrange notation, attributed to the Italian mathematician Joseph-Louis Lagrange. This notation uses the symbol f’ (read as “f prime”) or f’(x) (read as “f prime of x”) to refer to the derivative of the function.

For example, the derivative of the function f(x) = x² is the function 2x. Hence, we can write this derivative function using the Lagrange notation as f’(x) = 2x. 

The second notation is the Leibniz notation, attributed to the German mathematician Gottfried Wilhelm von Leibniz. It uses the symbol dy/dx to indicate the function f(x) derivative. Where did the “y” come from? Recall that y = f(x), as discussed in our review of functions. Hence, when we say dy/dx, we assume y refers to a function. 

We usually use the Lagrange notation when the given function is expressed with f(x). For instance, the derivative of f(x) = x² is written as f’(x) = 2x. On the other hand, we usually use the Leibniz notation when the given function is expressed with y. For instance, the derivative of y = x² is written as dy/dx = 2x.

Now that you know the notation used for derivatives, let us discuss the techniques we can use to identify them. 

Differentiation Rules

To find the derivative of a function, we apply the following differentiation rules:

1. Derivative of a Constant

“The derivative of a constant is zero.”

Recall that every real number is a constant. Hence, if we take the derivative of a real number or a constant, it is always zero (0).

Sample Problem 1: What is the derivative of -5?

Solution: -5 is a constant, so its derivative is simply 0.

Sample Problem 2: What is the derivative of π?

Solution: π is also a constant, so its derivative must be 0.

2. General Rule for Differentiation (Power Rule)

“The derivative of a function f(x) = xⁿ is nx^{n – 1} such that x is variable and n is constant.”

The Power Rule, also called General Rule for Differentiation, provides the general technique to find the derivative of a variable raised to any real number.

According to this rule, the derivative of xⁿ, where x is a variable while n is a constant, can be obtained by these steps:

1. Multiply the variable x by the constant n to get nx.
2. Raise x to n – 1, where n is a constant

Here’s an example:

Sample Problem 1: Use the power rule to determine the derivative of f(x) = x⁶

Solution: Using the power rule, we can perform these steps:

Step 1: Multiply the variable x by the constant n to obtain nx.

We have n = 6 here, so multiply x by 6 to obtain 6x.

Step 2: Raise x to n – 1, where n is a constant.

We already have 6x and need to raise x to n – 1. Recall that n = 6. So, n – 1 = 5.

Thus, we have 6x⁵.

Therefore, the derivative of f(x) = x⁶ is f’(x) = 6x⁵.

Sample Problem 2: Identify the derivative of f(x) = x² 

Solution: 

Step 1: Multiply the variable x by the constant n to obtain nx.

We have n = 2 here, so multiply x by 2 to obtain 2x.

Step 2: Raise x to n – 1, where n is a constant.

We already have 2x and need to raise x to n – 1. Recall that n = 2. So, 2 – 1 = 1.

Thus, we have 2x¹ or simply 2x.

Therefore, the derivative of f(x) = x² is f’(x) = 2x.

Sample Problem 3: Determine the derivative of f(x) = x

Solution: 

Note that we can write the function x as x¹. Let us use the steps for applying the power rule:

Step 1: Multiply the variable x by the constant n to obtain nx.

We have n = 1 here, so we multiply x by 1 to obtain 1x or simply x.

Step 2: Raise x to n – 1, where n is a constant.

We have n = 1. Thus, 1 – 1 = 0. This means that we should raise x to the power of 0.

This means that we have x⁰. 

However, remember that any quantity raised to 0 equals one according to the zero-exponent rule.

Hence, x⁰ = 1. This means that the derivative of f(x) = x is 1.

3. Derivative of Constant Multiplied by a Function Rule (Multiplication by Constant Rule)

“If k is a constant and f(x) is a function, then the derivative of k * f(x) is k * f’(x).”

This property tells us that to identify the derivative of the product of a constant and a function, we take the function’s derivative and then multiply the resulting derivative by the given constant.

Sample Problem 1: What is the derivative of f(x) = 2x⁵?

Solution: Note that 2x⁵ is the product of a constant (which is 2) and a function (x⁵). Hence, we have to get the derivative of the function x⁵ first, then multiply the result by 2:

The derivative of x⁵ can be obtained using the power rule. 

Step 1: Multiply the variable x by the constant n to get nx.

We have n = 5 here, so multiply x by 5 to get 5x.

Step 2: Raise x to n – 1, where n is a constant.

We already have 5x and need to raise x to n – 1. Recall that n = 5. So, 5 – 1 = 4.

Thus, we have 5x⁴.

Hence, we have 5x⁴.

We multiply 5x⁴ by the constant of 2x⁵ (which is 2): 2 * 5x⁴ = 10x⁴.

Hence, the derivative of f(x) = 2x⁵ is f’(x) = 10x⁴.

Sample Problem 2: Identify the derivative of f(x) = 7x⁴.

Solution: 

This time, let us solve the derivative as briefly as possible. Don’t be confused by the brevity of the solution; we only apply the derivative of the constant multiplied by a function rule.

f(x) = 7x⁴

f’(x) = 7 * 4x³ By power rule, the derivative of x⁴ is 4x³

f’(x) = 28x³

Sample Problem 3: Compute the derivative of the function f(x) = 11x⁹.

Solution:

f(x) = 11x⁹

f’(x) = 11 * 9x⁸ By power rule, the derivative of x⁹ is 9x⁸

f’(x) = 99x⁸

Sample Problem 4: Solve for dy/dx if y = 9x⁷.

Solution: Recall that the dy/dx notation or the Leibniz notation only implies that we are looking for the derivative of y = 9x⁷. We can apply the derivative of a constant multiplied by a function rule:

y = 9x⁷

dy/dx = 9 * 7x⁶ By power rule, the derivative of x⁷ is 7x⁶

dy/dx = 63x⁶

The answer is 63x⁶.

4. Sum Rule

“The derivative of the sum of two functions is equal to the sum of the respective derivatives of the functions.”

In symbols, the derivative of f(x) + g(x) is f’(x) + g’(x)

This rule tells us that if two functions are added, the derivative of their sum is just the sum of the respective derivative of the addends.

Consider f(x) = x² + x³. This function is composed of x² and x³. The derivative of f(x) can be obtained by taking the respective derivatives of x² and x³ using the power rule and then adding these derivatives:

Hence, the derivative of f(x) = x² + x³ is f’(x) = 2x + 3x²

Sample Problem: Identify the derivative of f(x) = x⁵ + 2x⁴ + 3x²

Solution: Since the derivative of f(x) can be obtained by getting the respective derivatives of x⁵, 2x⁴, and 3x² and then adding them, we have: 

Hence, the answer is f’(x) = 5x⁴ + 8x³ + 6x.

5. Difference Rule

“The derivative of the difference of two functions is equal to the difference of the respective derivatives of the functions.”

In symbols, the derivative of f(x) – g(x) = f’(x) – g’(x)

The difference rule is just the subtraction counterpart of the Sum Rule for Derivatives. If we want to identify the derivative of the difference between two functions, we need to subtract the derivative of the functions.

Sample Problem 1: Identify the derivative of f(x) = x⁴ – x³

Solution: The derivative of x⁴, determined using the power rule for derivatives, is 4x³.

Meanwhile, the derivative of x³, determined using the power rule for derivatives, is 3x².

Hence, the derivative of f(x) = x⁴ – x³ is the difference between the respective derivatives of x⁴ and x³ (4x³ and 3x², respectively). 

Therefore, the answer is f’(x) = 4x³ – 3x².

Sample Problem 2: Identify the derivative of f(x) = 2x³ – x

Solution: The derivative of f(x) = 2x³ – x can be obtained by getting the derivative of 2x³ and x using the power rule and then subtracting them:

Hence, the derivative of f(x) = 2x³ – x  is f’(x) = 6x² – 1.

Sample Problem 3: Compute the derivative of f(x) = x⁵ + 2x³ – 7x².

Solution: Notice that this problem’s given function uses addition and subtraction. We can identify the derivative of this function by determining the derivative of each term and then retaining the operations.

Therefore, the derivative of f(x) = x⁵ + 2x³ – 7x² is f’(x) = 5x⁴ + 6x² – 14x.

6. Product Rule

“The derivative of the product of two functions is equal to the sum of the product of the derivative of the first function and the second function, and the product of the derivative of the second function and the first function.”

In symbols: The derivative of f(x) g(x) = [f’(x) * g(x)] + [g’(x) * f(x)]

The product rule allows us to identify the derivative of the product of two functions. 

I know that the product rule is not that intuitive. For this reason, we will perform the product rule using the steps below:

1. Obtain the derivative of the first function.
2. Multiply the result you obtained in Step 1 by the second function.
3. Obtain the derivative of the second function.
4. Multiply the result you obtained in Step 3 by the first function.
5. Add the products you have obtained in steps 2 and 4. The result is the derivative of the product of the functions.

Let us answer some examples to help us understand this differentiation rule:

Sample Problem: What is the derivative of f(x) = (x + 2)(x² – 1)?

Solution: 

Step 1: Obtain the derivative of the first function.

The first function is x + 2. Obtaining its derivative:

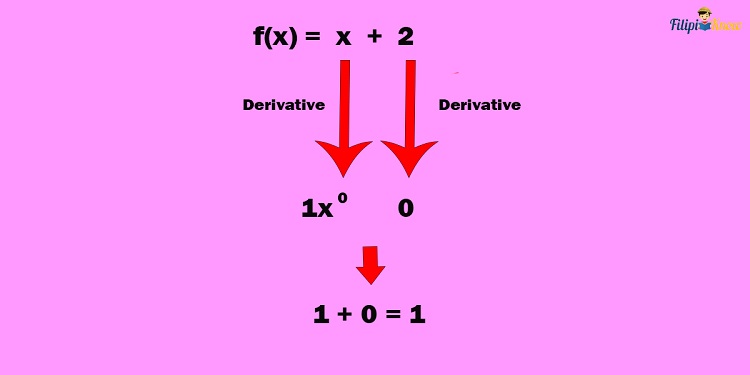
Hence, the derivative of x + 2 is simply 1.

Step 2: Multiply the result obtained in Step 1 by the second function.

We multiply one by the second function, which is x² – 1. 

1 * (x² – 1) = x² – 1. 

So, for this step, we have x² – 1.

Step 3: Obtain the derivative of the second function.

The second function is x² – 1. Obtaining its derivative:

Hence, we have 2x as the derivative of x² – 1.

Step 4: Multiply the result you obtained in Step 3 by the first function.

We multiply 2x by the first function, which is x + 2. Therefore, we have 2x * (x + 2) or just 2x(x + 2).

Step 5: Add the products you have obtained in steps 2 and 4. The result is the derivative of the product of the functions.

Note that in step 2, we got x² – 1; in step 4, we got 2x(x + 2).

Thus, adding these values will result in x² – 1 + 2x(x + 2).

We can simplify the expression above as 

x² – 1 + 2x(x + 2)

x² – 1 + 2x² + 4x Distributive Property

3x² + 4x – 1 Combining similar terms

Hence, the derivative of f(x) = (x + 2)(x² – 1) is f’(x) = 3x² + 4x – 1. 

7. Quotient Rule

“The derivative of the quotient of two functions is equal to the difference between the product of the denominator and the derivative of the numerator and the product of the numerator and the derivative of the denominator, divided by the square of the denominator.”

In symbols: the derivative of 

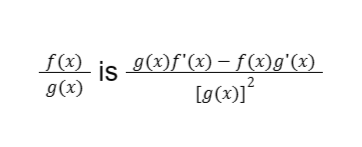
A powerful tool that helped me understand how to apply the quotient rule is the following short poem:

“Low dee high minus high dee low square the bottom and way we go.”

In this poem, low means the denominator, dee means “derivative,” and high means the numerator. 

Low dee high means denominator (low) times the derivative (dee) of the numerator (high).

High dee low means numerator (high) times the derivative (dee) of the denominator (low).

Next, you subtract the results you have obtained from “low dee high” and “high dee low.”

Meanwhile, square the bottom means square the denominator.

Lastly, we divide the difference between the “low dee high” and “high dee low” by the “square of the bottom.”

You can also remember the “shorter” version of the poem:

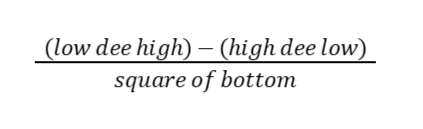
Isn’t it easier to deal with math if we remember the formulas in a fun way?

Let us try to apply this technique through an example. 

Sample Problem: Determine the derivative of the following 

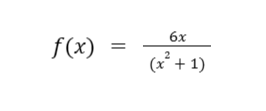
Solution:

• The numerator is 6x, so this will be the “high.”
• Meanwhile, the denominator is x² + 1, which will be the “low.”
• The derivative of the numerator, 6x, is just 6. So, our “dee high” is 6.
• The derivative of the denominator, x² + 1, is just 2x. So our “dee low” is 2x.

Let’s get “low dee high” first. “Low” is x² + 1 while “dee high” is 6. So, “low dee high” is 6*(x² + 1).

Now, let us obtain “high dee low.” The “high” is 6x while the “dee low” is 2x. So, “high dee low” is 6x*(2x).

Meanwhile, the square of the bottom is just the square of (x² + 1), which is (x² + 1)².

Let us now complete the “shorter” version of the poem:

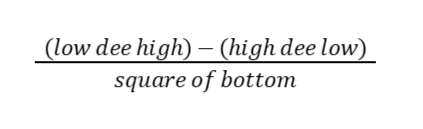
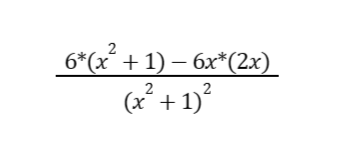
Let’s simplify the expression above:

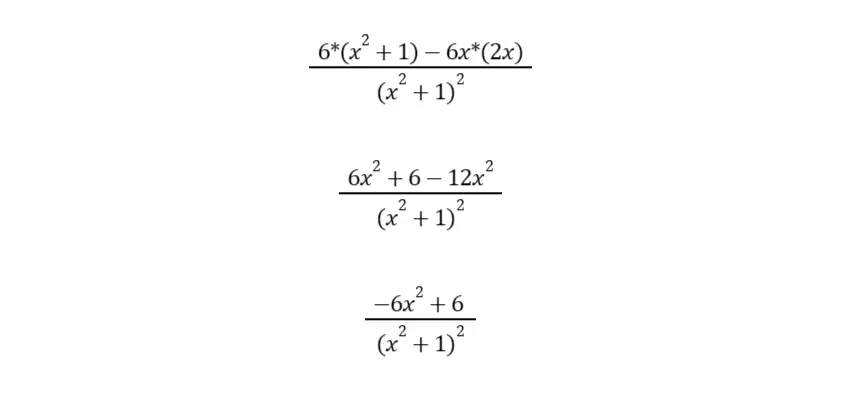
Thus, the answer to this problem is:

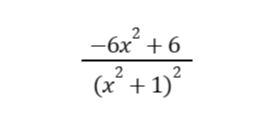
The expanded form of this expression is:

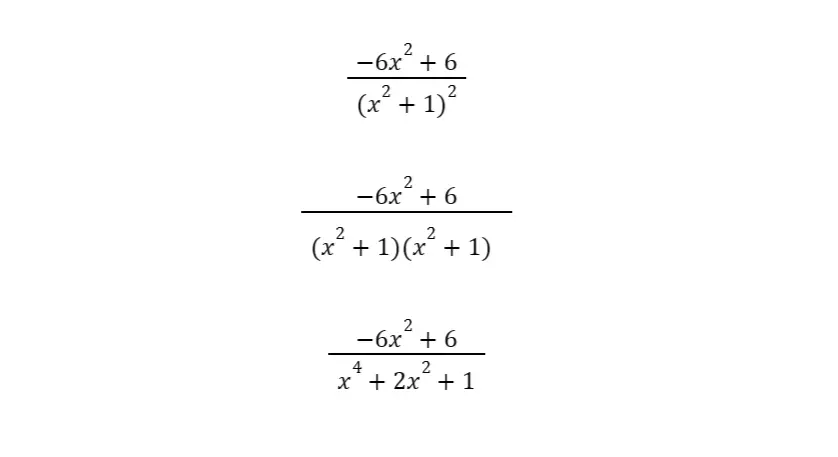
Differentiating a Composition of Functions

Do you still remember the composition of functions? Simply put, this function is “inside” or contained by a function. For example, in f(x) = x² and g(x) = x + 1, the composite function f(g(x)) means that we put g(x) inside f(x):

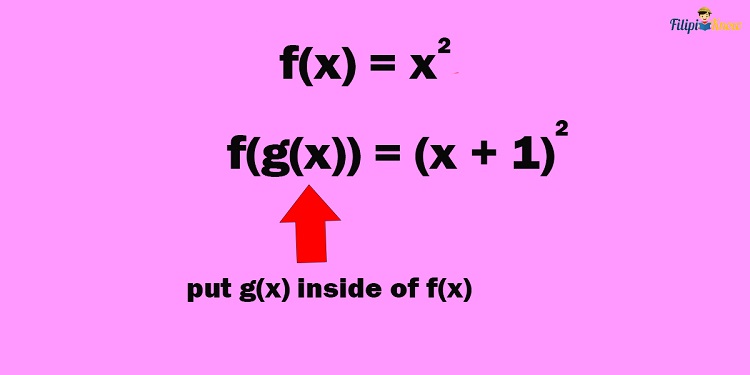
Thus, the composite function f(g(x)) is equal to (x + 1)².

In a composite function, you must identify the outer and inner functions. The outer function is where you plug in or insert the inner function. 

In f(g(x)) = (x + 1)², the outer function is x² since it is the one where you insert x + 1 (which is the inner function). 

Sample Problem 1: Identify the outer and inner functions of the composition f(x) = (x – 3)³

Solution: (x – 3)³ can be broken down into x³ as the outer function and x – 3 as the inner function. Note that as you plug in x – 3 to x³, you will obtain (x – 3)³.

Sample Problem 2: Identify the outer and inner functions of the composition f(x) = (3 + x²)²

Solution: The given function can be broken down into x² as the outer function and 3 + x² as the inner function. You will obtain the given function as you plug in 3 + x² to x².

Chain Rule

The chain rule is a special differentiation rule that allows us to identify the derivative of a composite function.

The chain rule states that “the derivative of the composition of a function is the derivative of the outer function evaluated at the inner function times the derivative of the inner function.”

In symbols: D[f(g(x))] = f’(g(x)) g’(x)

To make it easier for us to apply the chain rule, we will perform it using the steps below:

1. Identify the outer and inner functions.
2. Take the derivative of the outer function.
3. Evaluate the derivative of the outer function at the inner function.
4. Take the derivative of the inner function.
5. Multiply the result in Step 3 by the result in Step 4.

Sample Problem 1: Use the chain rule to differentiate f(x) = (x + 7)²

Solution: Let us apply the chain rule to differentiate (x + 7)².

Step 1: Identify the outer and inner functions. 

The outer function is x^2, and the inner function is x + 7.

Step 2: Take the derivative of the outer function.

By applying the power rule, the derivative of the outer function x² is simply 2x.

Step 3: Evaluate the derivative of the outer function at the inner function.

We perform this by simply plugging the inner function into the derivative of the outer function. Again, the inner function is x + 7, while the derivative of the outer function is 2x. Hence, we have the following:

2x

2(x + 7) Plug-in x + 7

Hence, we have 2(x + 7)

Step 4: Take the derivative of the inner function.

The inner function is x + 7, and by applying the differentiation rules we have learned, its derivative is 1.

Hence, we have 1.

Step 5: Multiply the result in Step 3 by the result in Step 4.

The result in step 3 is 2(x + 7), while for step 4, the result is 1.

Multiplying them: 2(x + 7) * 1 = 2(x + 7)

The answer is 2(x + 7).

Sample Problem 2: Use the chain rule to identify the derivative of (x² – 9)⁵

Solution: 

Step 1: Identify the outer and inner functions. 

The outer function is x^5, and the inner function is x² – 9.

Step 2: Take the derivative of the outer function.

By applying the power rule, the derivative of the outer function x⁵ is simply 5x⁴.

Step 3: Evaluate the derivative of the outer function at the inner function.

We perform this by simply plugging the inner function into the derivative of the outer function. The inner function is x² – 9, so we plug in this function to the computed derivative of the outer function, which is 5x⁴. 

5x⁴

5(x² – 9)⁴ Plug-in x² – 9

Hence, we have 5(x² – 9)⁴. 

Step 4: Take the derivative of the inner function.

The inner function is x² – 9. Applying the differentiation rules we learned in the previous section, its derivative must be 2x.

Step 5: Multiply the result in Step 3 by the result in Step 4.

The result in step 3 is 5(x² – 9)^4, while step 4’s result is 2x.

Multiplying them: 5(x² – 9)⁴ *  2x = 10x(x² – 9)⁴

The answer is 10x(x² – 9)⁴.

Derivatives of Other Functions (Optional)

In this section, you’ll get an overview of the derivatives of other functions, such as the exponential and trigonometric functions.

1. Derivative of an Exponential Function

An exponential function is a function whose value is a constant raised to a specific variable.

For instance, f(x) = 2^x, g(x) = 3^x, h(x) = 9^0.10x, r(x) = 0.9x⁴ are all examples of exponential function.

Generally, an exponential function is in the form f(x) = a^x, where a is a constant and x is a variable. 

What is the derivative of an exponential function?

The derivative of an exponential function f(x) = a^x is f’(x) = a^x ln x, where ln pertains to the “natural logarithm,” a special function used in algebra and calculus. Technically, this is the logarithm of a number to the base e (the concept of logarithms is beyond the scope of our reviewer, so we take this as it is).

Sample Problem: Find the derivative of f(x) = 3^x 

Solution: The derivative of an exponential function f(x) = a^x is just f’(x) = a^x ln x. Hence, the derivative of f(x) = 3^x must be f’(x) = 3^x ln x. 

2. Derivative of Trigonometric Functions

Shown below are the derivatives of the trigonometric functions which we discussed in our trigonometry review. We will not discuss how their derivatives were derived because the “math” behind them is complicated.

Trigonometric Function	Derivative
Sin x	Cos x
Cos x	-Sin x
Tan x	Sec2x
Csc x	–csc x cot x
Sec x	Sec x tan x
Cot x	-csc2x

Geometric Interpretation of the Derivative of a Function

The derivative of a function refers to the rate of change of a function with respect to its variable. Geometrically, this is the slope of the line that is tangent to the function’s graph. 

Consider the graph of the function below.

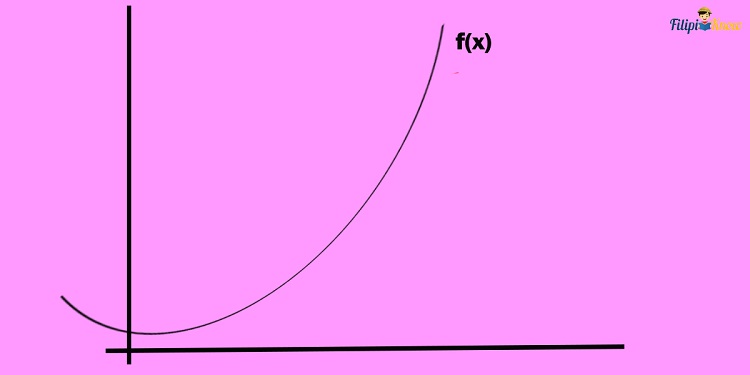
Obtaining its slope is not straightforward since the function above is a curve. In other words, we cannot use the slope formula or the techniques we have discussed in identifying the slope of a line.

What we are going to do is to take a point on this curve. Let us label this point as (x, y).

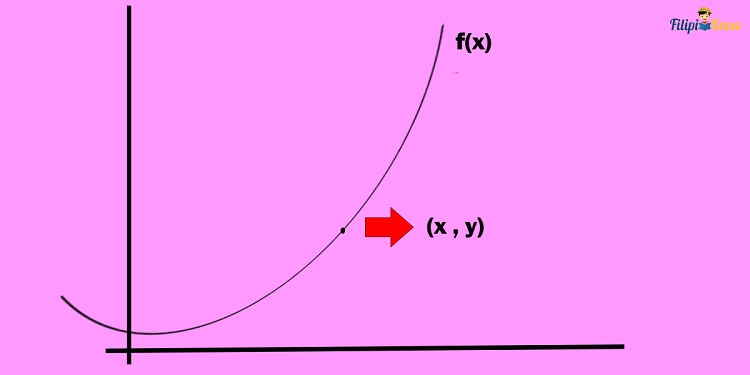
Suppose we add some arbitrary constant to x, say ∆x, and y, say ∆y so that the resulting point will be on the curve. This resulting point will be the point (x + ∆x, y + ∆y). 

Since we are dealing with a function, let us use f(x) instead of y.

Hence, the point (x, y) can be written as (x, f(x)), and the point (x + ∆x, y + ∆y) can be written as (x + ∆x, f(x + ∆x)). 

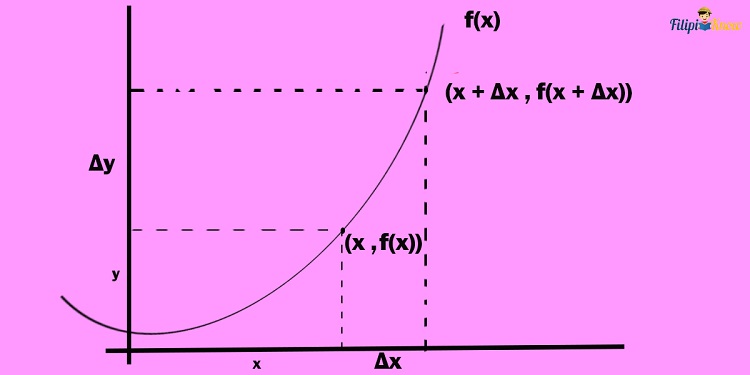
Connect these two points in a straight line. Let us call this line l₁

Using the points (x, y) and(x + ∆x,  f(x +∆x)), we can calculate the slope of line l₁: Recall that the formula for slope is

where (x₁, y₁) and (x₂, y₂) are coordinates of the line. 

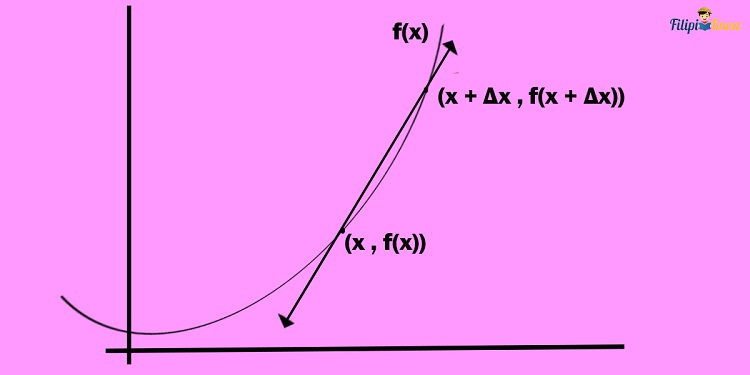
Hence the slope of line l₁ can be expressed as

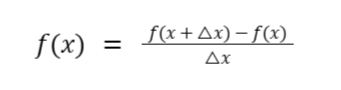
However, we are not interested in the slope of line l₁. Remember that the derivative of a function (or a curve) is the slope of the tangent line. The tangent line of the given curve would look like what’s shown below. The tangent line is the one colored in red.

Now from the slope of line l₁, how can we derive the slope of the red-colored line or the tangent line, which is also the derivative of this function or curve? 

Notice that if we let the value of ∆x be smaller and smaller, we will achieve the slope of the red line from the slope of l₁. In other words, we must make the value of ∆x closer and closer to 0. 

Hence, the slope of the tangent line of a curve and its derivative is defined by:

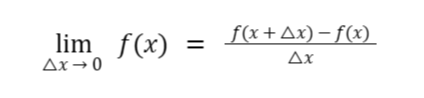
Sample Problem: Find the derivative of f(x) = x² using the definition of the derivative.

Solution:

We have f(x) = x². This means that by adding an arbitrary constant, ∆x, we have f(x + ∆x) = (x + ∆x)²

By square of binomial: f(x + ∆x) = (x + ∆x)² = x² + 2x∆x + ∆x²

Using the definition of the derivative:

From our calculation, the derivative of f(x) = x² is 2x. 

Fortunately, we don’t have to do the long and intimidating method above in taking the derivative of a function. The differentiation rules we have learned in this review are already enough for you to obtain the derivative of a function.

Next topic: Basic Integration

Previous topic: Limits

Return to the main article: The Ultimate Basic Math Reviewer

Download Printable Summary/Review Notes

Download Printable Flashcards

Test Yourself!

1. Practice Questions [Free PDF Download]

2. Answer Key [Free PDF Download]

3. Math Mock Exam + Answer Key